奇合数的构成规律研究

康湘兰，周东平

（1.利欧股份有限公司，温岭317500；2.温岭市新河中学，温岭317500）

0 引 言

合数是与素数相对应的概念.除了1和本身之外，还可以被其它自然数整除的数称为合数.既是合数又是奇数的数被称为奇合数.即奇合数就是能够被除1和本身以外其他一个或几个自然数整除的正奇数.例如：9、15、21等都是奇合数.

正奇数集是由1与奇合数及素数组成的.对于素数的构成规律有大量的研究，但是最好的研究结果还是中国陈景润得出的“1＋2”.本文就奇合数的构成规律进行探究，试图从素数与奇数相乘构成奇合数的关系着手找出奇合数的构成规律，从而为研究素数分布提供方便.

1 素数与奇数的乘积构成奇合数

所有的奇合数可以看成是由一个素数和一个奇数的乘积来生成的，每个素数都可能生成一系列的奇合数，例如：9＝3＊3，15＝3＊5，125＝5＊25等等.通过公式它们可以表示为：

这些公式中的n是不确定的，能否有确定的公式来表达奇合数，下面一起去探寻.

2 奇合数构成规律

假设某一素数a n与其相邻的下一个素数a n＋1的平方之间的奇合数要么是由a n前面的素数与某一奇数相乘生成的，要么是由a n本身与某一奇数相乘生成的.下面以上述5个公式为例，对奇合数组成规律进行分析研究.

2.1 素数a 1＝3生成的奇合数的规律

根据公式①，我们计算出100以内由3产生的奇合数如表1所示.

表1 100以内由3产生的奇合数

通过归纳法，可以找到通项公式为：y1＝6n＋3×3（n＝0，1，2……），此为首项为9，公差为6的等差数列.

2.2 素数a 2＝5生成的奇合数的规律

根据上述公式②，我们计算出500以内由5产生的奇合数如表2所示.

表2 500以内由5产生的奇合数

2.3 素数a 3＝7生成的奇合数的规律

根据上述公式③计算650以内由7产生的奇合数如表3所示.

表3 八组由7生成的奇合数

通过归纳法，可以找到8个通项公式，它们为8个不同首项、相同公差的等差数列，如表4所示.

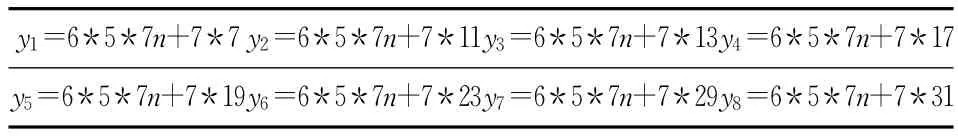
表4 八组通项公式表达式

其中表2中的n＝0，1，2…….其中本文中的“＊”为乘积符号.

2.4 素数a 4＝11生成的奇合数的规律

根据上述公式④计算9260以内由11产生的奇合数，共可分为48组，如表5所示.

表5 四十八组由11生成的奇合数

通过归纳法，可以找到48个通项公式，他们为48个不同首项，相同公差的等差数列，如表6所示.

表6 四十八组等差数列的表达式

其中表4中的n＝0，1，2…….

2.5 素数a 5＝13生成的奇合数的规律

根据公式⑤计算90260以内由13产生的奇合数，共可分为481组，部分这样的奇合数如表7所示.

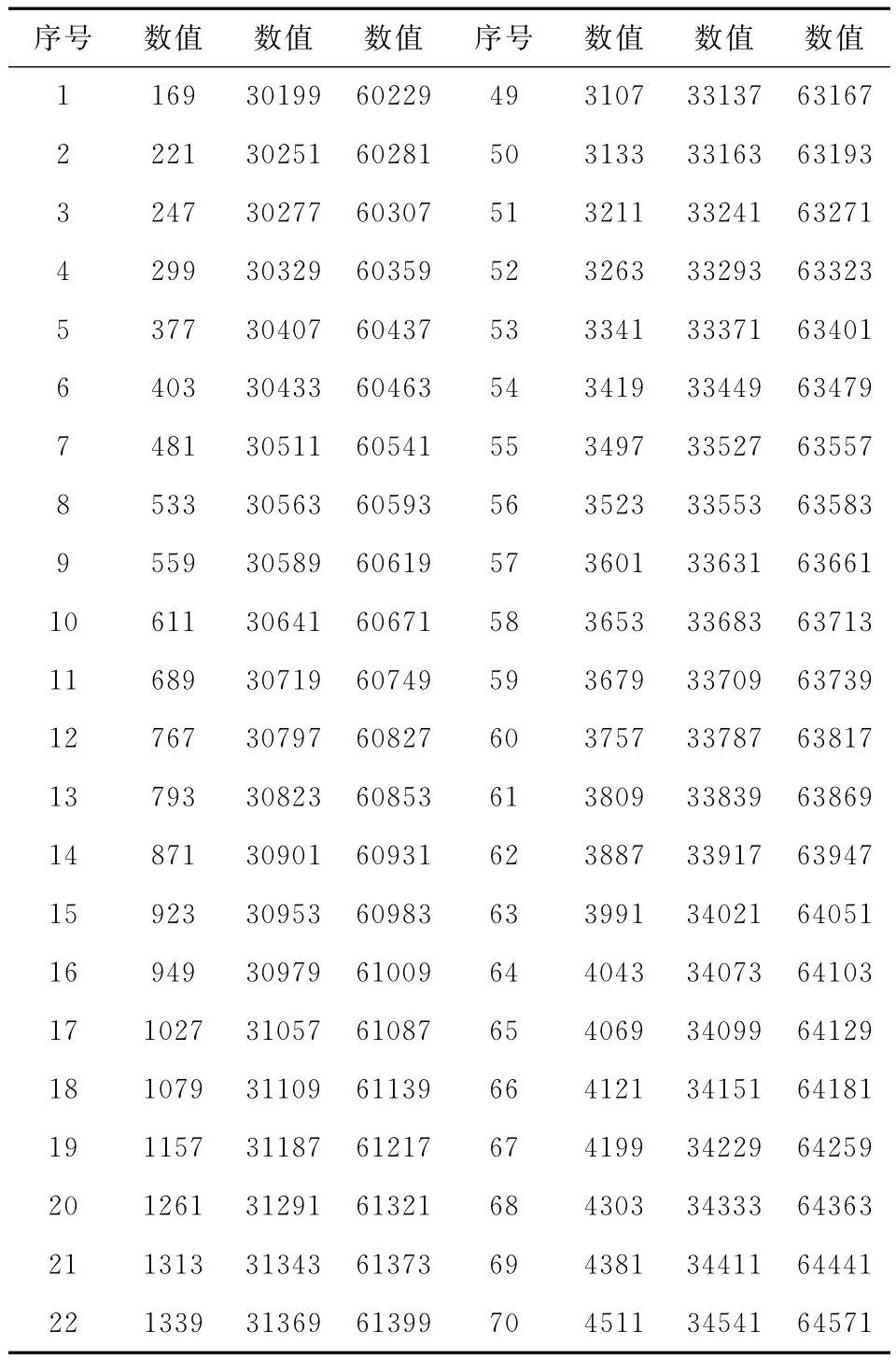
表7 部分由13生成的奇合数

23 1391 31421 61451 71 4537 34567 64597 24 1417 31447 61477 72 4589 34619 64649 25 1469 31499 61529 73 4667 34697 64727 26 1651 31681 61711 74 4693 34723 64753 27 1703 31733 61763 75 4771 34801 64831 28 1781 31811 61841 76 4849 34879 64909 29 1807 31837 61867 77 4901 34931 64961 30 1937 31967 61997 78 4927 34957 64987 31 1963 31993 62023 79 4979 35009 65039 32 2041 32071 62101 80 5057 35087 65117 33 2119 32149 62179 81 5083 35113 65143 34 2171 32201 62231 82 5161 35191 65221 35 2197 32227 62257 83 5213 35243 65273 36 2249 32279 62309 84 5239 35269 65299 37 2327 32357 62387 85 5317 35347 65377 38 2353 32383 62413 86 5447 35477 65507 39 2483 32513 62543 87 5473 35503 65533 40 2509 32539 62569 88 5603 35633 65663 41 2561 32591 62621 89 5629 35659 65689 42 2587 32617 62647 90 5681 35711 65741 43 2743 32773 62803 91 5707 35737 65767 44 2873 32903 62933 92 5759 35789 65819 45 2899 32929 62959 93 5837 35867 65897 46 2951 32981 63011 94 5941 35971 66001 47 2977 33007 63037 95 5993 36023 66053 48 3029 33059 63089 96 6019 36049 66079

通过归纳法，可以找到481个通项公式，它们为481个不同首项，相同公差的等差数列.这些公式与表7中数据一一对应.部分通项公式如表8所示，

表8 部分等差数列的表达式

其中表6中的n为：0，1，2，…….

3 结 论

根据上面的分析，可以得出以下结论：

奇合数集合可以分解由素数生成的无数个等差数列，即奇合数集合可以表示为无数个等差数列的并集.等差数列的形式可以表示为：Y＝Cn＋B，B为等差数列的首项，C为等差数列的公差，n为非负整数.其中由素数a1生成的奇合数的等差数列可以表示为Y＝6n＋3×3（n为非负整数），由其他的素数an生成的奇合数的等差数列Y＝Cn＋B表达式中，C可以表示为：6×a2×a3×…，×an，B可以表示成为a n×N，其中N是包含[an，6×a2×a3×…×an－1]之间所有素数的非连续整数集合，其中里面的整数不包括an之前任何一个素数形成的奇合数.

[1]潘承洞.素数分布与哥德巴赫猜想[M].山东科学技术出版社，1979.

[2]周海中.梅森素数的分布规律[J].中山大学学报，1992，31（4）.