基于有限单元法轮对-车轴系统动力学特性研究
2021-01-11王滋昊王美令马思群
王滋昊,王美令,马思群
(大连交通大学 机车车辆工程学院,辽宁 大连 116028)*
轮对-车轴系统作为轨道交通车辆的重要组成部分,起着承载驱动车身的作用,承受着车体和轨道载荷,受力复杂,目前随着轨道交通车辆朝着高速、重载的方向发展,研究其动力学特性也越来越重要和迫切.
在轨道交通车辆的动力学研究中,常将轮对的运动视为在钢轨上的平动[1].但在列车实际服役过程中,车轴因为自重等原因会产生弹性变形,车轴会偏离中心轴线,在轮对旋转过程中会产生动态作用力,对系统的动力学性能造成影响.目前国内外对于旋转轮对的研究相对较少.Fayos 基于旋转梁理论[2],考虑旋转惯性和陀螺效应建立了轮对的动力学模型.Bazea[3]利用Fayos的模型对轮轨的高频振动特性进行了研究.Jose Martinez-Casas[4]综合考虑弹性圆柱体旋转特性与模态阻尼,对轮对旋转状态下的应力分布特征进行了仿真分析.闻方宇[5]基于ANSYS/DYNA模拟了旋转轮对通过道岔时的车轮接触状态.徐宁等[6]采用假设模态法对带有集中质量和转动惯量的弹性车轴振动特性进行了分析.钟硕乔等[7]研究了轮对弯曲模态对轮轨接触性能的影响.张宝安等[8]考虑轮对旋转行走建立了弹性轮对与刚性轨道的接触模型,研究了弹性轮对振动对车辆动力学性能的影响.杨光[9]综合考虑了轮对的弹性与旋转行走,对轮轨系统的动力学性能进行了研究.杨柳等[10]基于哈密尔顿最小势能原理建立了机车转子非线性系统的动力学模型,研究了复杂边界条件下,非线性因素对转子系统的影响.综上所述,目前针对弹性旋转轮对动力学特性研究多是基于传统的车辆动力学研究方法,利用相关有限元软件、动力学软件进行仿真模拟.结合转子动力学的理论,采用数值方法进行求解的相关研究较少.
本文提出了一种基于有限元单元法的弹性轮对-车轴系统建模方法,分析了轮对-车轴系统动力学特性,为轮对-车轴的动力学理论及振动分析提供理论基础.
1 轮对-车轴系统模型建立
1.1 轮对-车轴系统动力学模型
如图1所示,轮对-车轴系统包括有车轴、车轮、轴承等部件,车轮与轨道相接触,轴承上部支撑着车体.
本文将利用转子动力学的相关理论对其特性进行分析,整个轮对-车轴系统由车轴两端轴承弹性支承,忽略车轴轴肩处过渡圆角,将车轴进行轴段划分,划分过程中需遵循以下原则[11]:①以轴段轴肩处作为划分点,以便于描述不同截面积的轴段特性;②以轴段受力位置作为划分点,以便于描述轴段的载荷特性;③轴段的划分尽量均匀,即轴段的长度的均匀性.
将划分后的每一轴段视为梁单元.将车轮视为刚性圆盘,忽略其自身幅板、轮辋等结构,在求解过程中将其等效为集中质量点固结在车轴上.可将作用于支点处的弹性支承等效为弹簧-阻尼单元.将自身结构、轮轨接触产生的载荷视为作用于整个系统的外界激励.所建立的模型如图2所示.
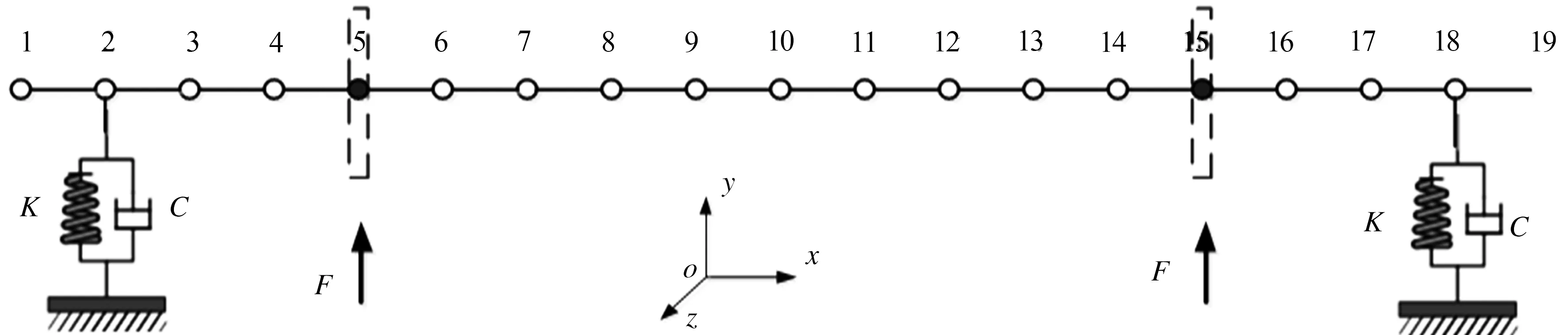
图2 轮对-车轴系统力学模型
针对图2中的轮对-车轴系统建立其动力学方程为
(1)

该动力学方程采用Newmark-β法进行求解.在转子系统的划分中,假设转子具有n个节点,系统具有4n个自由度,所形成的整体刚度、质量等矩阵为4n×4n阶方阵.系统的整体矩阵由各单元矩阵采用直接叠加法组装得到.以整体刚度矩阵的叠加为例,先将各单元的8×8阶刚度矩阵扩阶为4n×4n阶方阵,空位进行补0,然后将其进行叠加得到整体的刚度矩阵.弹性支撑的刚度直接叠加到对应节点上.
采用瑞利阻尼的形式引入系统的阻尼.将系统阻尼视为质量和刚度矩阵的线性组合,其形式为:
C=αM+βK
(2)

1.2 车轴—梁单元模型
在进行转子动力学的研究时,常将转子进行简单处理,建立起具有固定自由度数目的离散化转子模型.本文采用有限元方法,将车轴按照一定的原则进行划分,划分后的车轴单元为弹性单元,将其视为梁单元进行处理.每单元具有2个节点,在分析过程中,忽略其轴向变形,每个节点具有4个自由度.梁单元如图3所示.

图3 车轴-梁单元示意图
可以得到梁单元的广义位移为:
q=[vAwAθyAθzAvBwBθyBθzB]
(3)
忽略阻尼作用时梁单元的动力学方程为:
(4)
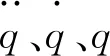
1.3 轮对-车轴系统中子模型
(1)集中质量模型
车轮通过过盈配合装配在车轴上,在实际处理过程中将其质量集中于节点处,将其视为质点固定于车轴上,等效为集中质量单元进行分析.
该模型质量矩阵Ml、陀螺矩阵Gl分别为:
(5)
(6)
(2)车轮激励载荷模型
铁道车辆的轮对在生产、组装过程中会产生偏心,而且在运行过程中,由于滚动磨耗及擦伤,也会导致车轮偏心[12].车轮偏心时,其质心与几何中心不重合,偏心距r0,激振载荷为:
F=mΩ2r0
(7)
式中,m为车轮质量,Ω为轮对-车轴转速,r0为偏心距.
将该激振载荷分解到y、z平面上可得
(8)
式中,φ为初始不平衡相位.
(3)轮轨接触法向载荷的计算
在车辆运行过程中,车轮与轨道接触,会产生蠕滑力,为研究轮对-车轴系统的振动特性,忽略轮轨接触蠕滑力的影响,仅考虑轮轨法向接触力.车轮节点轮轨法向接触力[1]为:
(9)
式中,G为轮轨接触常数,单位为(m/N2/3);δZN(t)为轮轨接触法向压缩量,单位为m.
对于磨耗形踏面,G=3.86R-0.115×10-8;对于锥形踏面,G=4.57R-0.149×10-8.其中R为车轮的滚动圆半径.
考虑轨道垂向不平顺Z(t)的情况下,轮轨法向接触力为:
(10)
2 轮对-车轴系统的固有特性
2.1 固有特性分析
按照本文第1章所述方法,以某铁路货车的轮对为研究对象,划分后的车轴模型如图4所示,各轴段参数如表1所示.

图4 划分后轴段

表1 轴段参数表 mm
在上述划分的轴段模型中,节点2、18为弹性支承的作用点,由于本文将车轮简化为质点叠加在车轴上,故将车轮按照名义滚动位置进行划分,即节点5、15为刚性车轮的等效质量点,其受到由于自身结构以及轮轨接触产生的载荷.
在整个模型中,节点2、节点18处弹性支撑,支撑刚度为1×108N/m,阻尼为1×103N·s/m,车轮质量ml=380.128 kg,集中惯性质量Il=20.41kg·m2,车轴的弹性模量取为205.8 GPa,密度取为7 850 kg/m3.
在ANSYS软件中建立轮对-车轴系统的有限元模型,弹性车轴的轴段利用pipe16单元进行模拟,车轮的集中质量点采用MASS21单元进行模
拟,采用COMBI214单元模拟两端的支撑轴承,其余参数设定均与一致,采用模态减缩法进行系统固有特性的求解.建立的有限元模型如图5所示.

图5 轮对-车轴系统有限元模型
分别利用两种算法计算得到的轮对-车轴系统振型如下表2中所示.
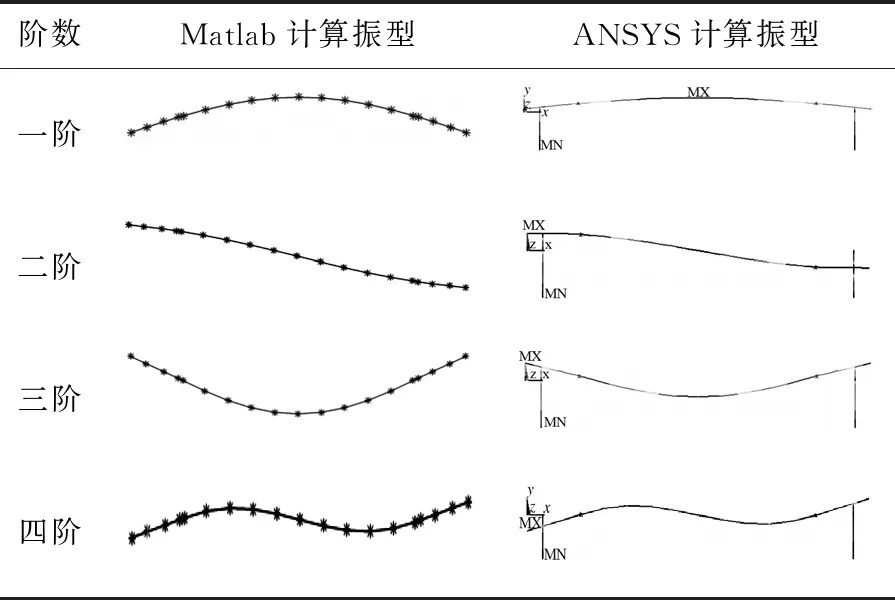
表2 ANSYS与Matlab有限元法计算振型图
如表2所示,两种计算方法所得轮对-车轴系统的振型一致,其一阶振型为一阶垂向弯曲、二阶振型均为二弯曲,三阶振型为一弯曲,其弯曲方向与一阶相反,四阶振型为二弯曲.
将Matlab与ANSYS计算得到的固有频率进行比对,如表3所示.
表3 ANSYS与Matlab有限元法计算固有频率对比

Hz
从表3可以看出,两种软件计算所得固有频率结果误差小于8%,且两种计算方法所得振型一致.因此可以验证仿真结果的正确性,证明了该轮对-车轴系统模型的准确性.
2.2 轮对-车轴系统临界转速分析
分别利用Matlab与ANSYS进行轮对-车轴系统坎贝尔图的绘制,并对其求取临界转速值.所得坎贝尔图如图6所示,临界转速值汇总于表4.
在图6(a)中,虚线表示不考虑陀螺效应时系统的涡动角速度,即系统的固有频率,其不随自转角速度的增大而发生变化,呈直线.作ω=Ω的直线与其他各曲线相交,交点即为相应的考虑陀螺效应时系统的同步正向、反向涡动临界转速.对比图6(a)、图6(b)可发现两者趋势一致.
由表4可以看出,两种计算所得出的临界转速值误差小于4%,表明该模型的准确性.

(a)Matlab计算所得坎贝尔图

(b) ANSYS计算所得坎贝尔图

r/min
根据转子动力学[13]的相关理论,当转子工作转速低于0.7倍一阶临界转速值时,可视为刚性转子,当工作转速大于0.7倍一阶临界转速值时需视为挠性转子.考虑到我国铁路仍有提速的前景,当列车运行速度达到325km/h时,轮对转速已经超过0.7倍一阶临界转速,需要将其视为挠性转子进行分析,因此有必要对轮对-车轴系统进行弹性化建模.
3 车轮偏心对轮对转子动力学影响
选取车轮偏心量为2 mm,车辆运行速度设定为80、100、120 km/h,计算轮轨法向作用力,得到结果如下图7所示.
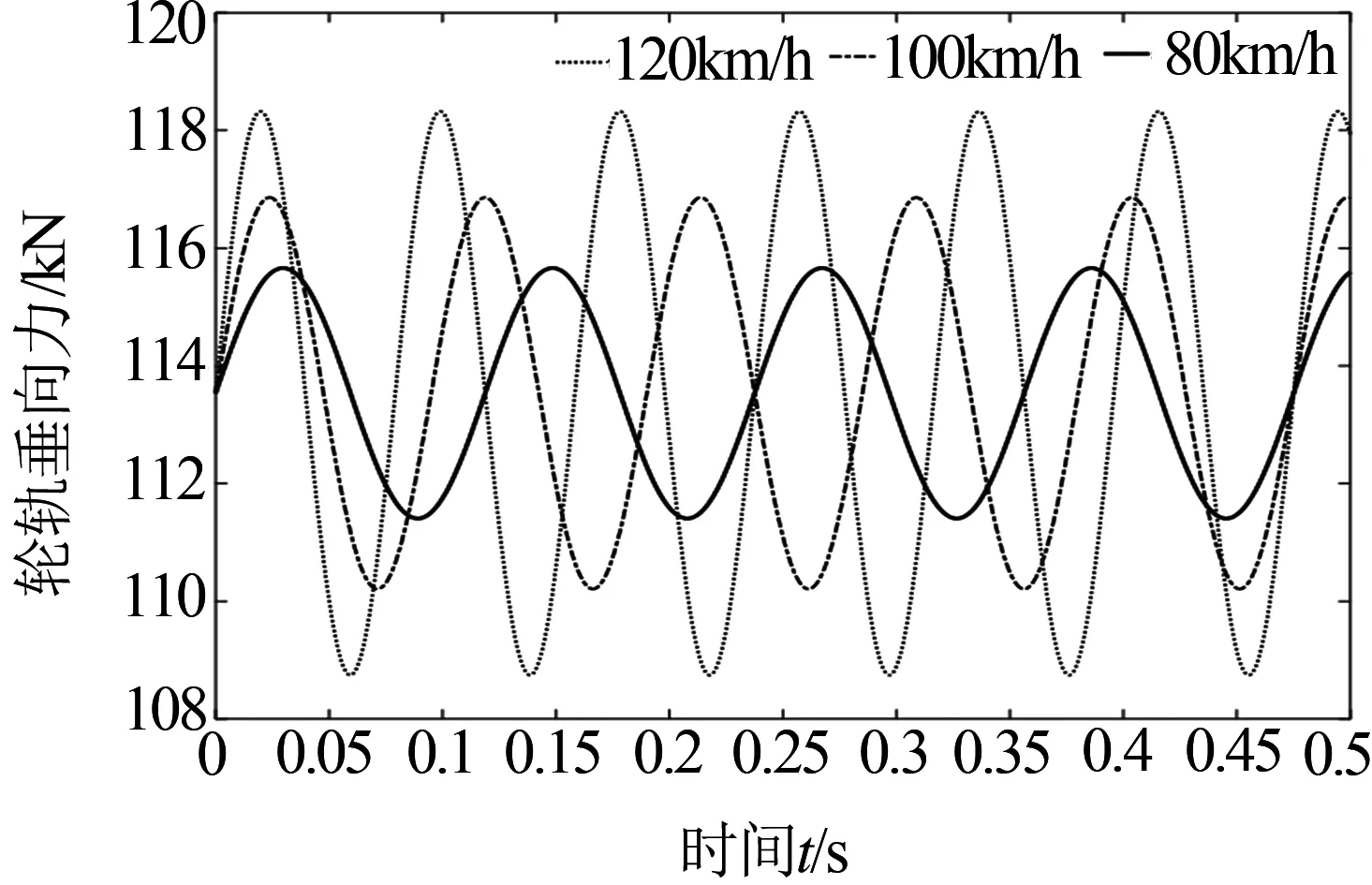
图7 不同运行速度下轮轨法向作用力
分别选取车轮偏心量为1.0、1.5、2.0与2.5 mm,得到动态法向轮轨作用力变化如图8所示.

图8 不同偏心量下法向动态作用力
由图7、8可知,当车轮纯滚动时,轮轨法向作用力呈周期变化,并且随着车辆运行速度的增加,作用力的幅值和频率也逐渐增大.随着车轮偏心距的增大,轮轨法向动态作用力也增大,并且车辆运行速度越快,增大的幅度越高.
4 结论
本文利用有限元方法建立了轮对-车轴系统模型,并进行动力学特性分析,得出如下结论.
(1)基于有限元单元方法建立了考虑车轴弹性的轮对-车轴系统动力学模型,利用Matlab与ANSYS对轮对-车轴系统求解固有特性,其所得振型结果一致,固有频率值误差小于8%,临界转速值误差小于4%.验证了模型准确性;
(2)轮对-车轴系统的前四阶振型主要为一弯曲和二弯曲振型,频率范围为46~292 Hz;
(3)当存在车轮偏心质量时,随着车轮偏心距和转速的增大,轮轨法向动态作用力增大.
