活性焦脱硫吸收塔的振动特性分析

房 翔，王 彪，黄志来

（安徽工业大学 机械工程学院，安徽 马鞍山 243002）

1 模态分析理论

模态分析的实质——坐标变换。变换的目的是将之前在物理坐标系统中表达的响应向量，放到模态坐标系统中进行表达，模态坐标系统中的每一个特征向量恰好对应之前物理坐标系统中的一个基向量[1-3]。一般来说，选取前几阶模态进行叠加即可达到路够的精度，使频响函数的矩阵阶数大大减小，减轻了计算工作量，这是模态分析法的一大优点。

在对大型机械结构进行模态分析时，一般是将连续结构离散化为一个具有n个有限自由度的多自由度离散系统。对于一个具有n个有限自由度的离散系统而言，将结构总质量矩阵定义为[M]，将结构总刚度矩阵定义为[K]，将结构总阻尼矩阵定义为[C]；离散系统的动激励载荷向量为{F(t)}，位移向量为{X(t)}，速度向量为系统加速度向量为其运动微分方程为：

对扇形段进行模态分析，外力作用无需考虑，即动激励载荷向量{F(t)}=0，由此能看出结构阻尼较小，因此其对固有频率和振型影响很小，可以忽略不计。在上述情况下，可将求解扇形段结构的振型和固有频率问题转化为求解扇形段的特征向量和特征值问题。因此，式（1）中的[C]=0，方程可简化为：

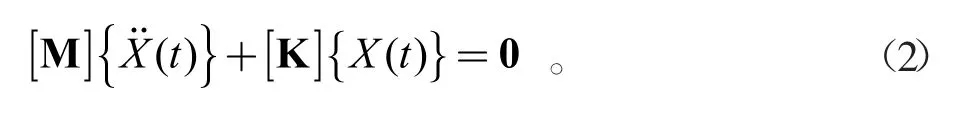
由于一系列简谐振动的叠加可以组成任何弹性体的自由振动，故可设式（2）的简谐振动解为：

式（3）中的ω是系统结构的固有频率。

将式（3）代入式（2）得：

又因自由振动时，机构各个节点的振动振幅不全为0。故有：

由于[K]和[M]矩阵的阶数均为n阶方阵，式（5）为ω2的n次实系数方程，解此方程可得到n个固有频率，也就得到所需的特征值ω和特征向量{X(t)}。所以系统的固有频率和振型求解问题就是求系统的矩阵特征值ω和特征向量{X(t)}的问题。

2 模态分析的步骤

模态分析过程实际上是一个线性分析过程，主要分为以下四步：建模、加载和求解、扩展模态、观察结果[4-7]。

2.1 建模

在前处理中定义单元类型、材料性质、边界条件等，需要注意以下两点：

（1）模态分析只对线性行为有效，如果定义了非线性单元，将当作线性单元来处理；

（2）由模态分析的基本理论可知，在模态分析中必须定义弹性模量和密度，否则不能计算，见表1。

表1 材料的属性

2.2 加载和求解

先进入Solution求解器，设定将要分析的类型和选项，施加载荷，然后设定加载步选项，最后求解计算有限元模型。

本文采取的正则模态分析方法是Lanczos迭代法，这种方法的优点是：可在分析过程中进行频移，在设定求解频率范围时，采用Sturm序列确定设定范围内的模态，所以可以确定并输出设定范围内的所有模态；可获得系统动力学分析结果，或者模型响应分析的强迫运动矩阵[4]。

2.3 扩展模态

观察到求解的振型，必须先将求解的振型读入结果文件，然后进行模态扩展。

2.4 观察结果

在后处理中，观察经过模态扩展后模态分析的结果文件，得到固有频率和模态振型。

3 百叶吸收塔模态分析

吸收塔及百叶的几何尺寸如图1所示。活性焦脱硫吸硫塔前10阶固有频率，见表2。对应的振型图如图2至图11所示。

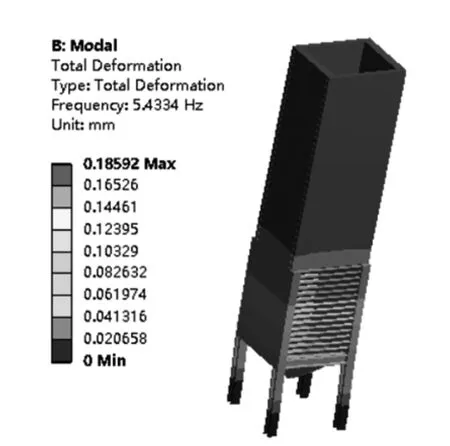
图2 第1阶振型图

表2 A型吸硫塔前10阶固有频率

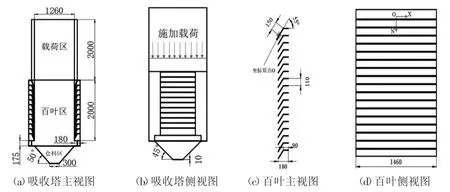
图1 吸收塔及百叶几何尺寸图

图3 第2阶振型图

图4 第3阶振型图

图5 第4阶振型图

图6 第5阶振型图

图7 第6阶振型图

从图2至图11所展示的10阶振型图中，可以看出第1阶振型图是在X-Z平面内发生弯曲振动；第2阶振型图是在Y-Z平面发生弯曲振动；第3阶振型图是绕Z轴方向发生的扭振；第4阶振型图是在X-Z平面发生S型弯曲振动；第5阶振型图是在Y-Z平面发生S型弯曲振动；第6阶振型是吸硫塔沿Z轴方向发生弯曲振动；第7阶振型在X-Y平面的对角线方向产生扭振，并沿Y-Z平面产生轻微的弯曲振动；第8阶振型图在X-Z平面产生较为明显的S型弯曲振动；第9阶振型图是在Y-Z平面产生双向弯曲振动，并绕Z轴方向产生较为明显的扭振；第10阶振型图的为X-Z平面的双向弯曲振动，并绕Z轴产生扭振。

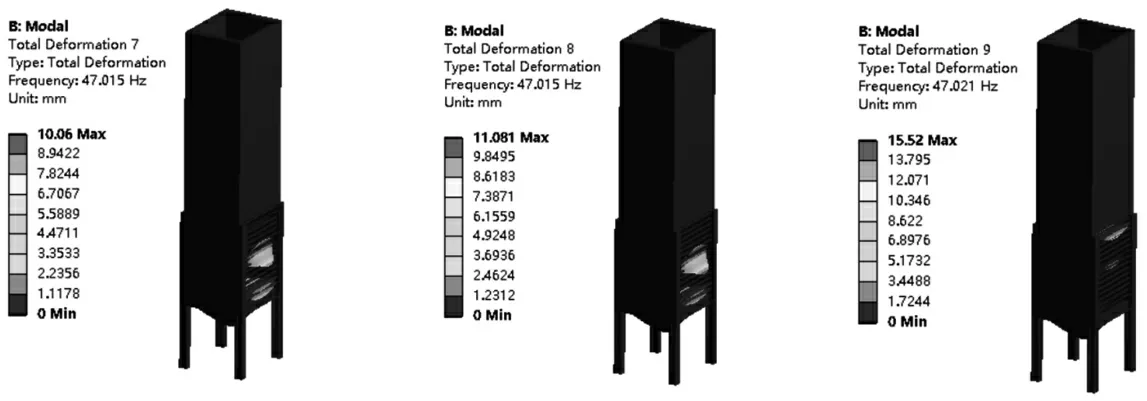
图1 0第9阶振型图

图1 1第10阶振型图

图8 第7阶振型图

图9 第8阶振型图

4 结束语

通过对该脱硫吸收塔进行有限元建模并进行模态分析，得到了这3种类型的吸收塔的前10阶模态的振型及对应频率，振型分布规律相似，只是频率有差异。当吸收塔在实际工作过程中，周围的频率源，比如电机等，要尽量避开塔的固有频率。在最终的工程应用中，没有出现振动引起的塔内活性焦颗粒外溢现象，表明这样的设计能有效避免振动问题。