枕下网孔式弹性垫板刚度阻尼特性研究
2021-01-11赵峰石广田魏晓和振兴张波张国帅
赵峰,石广田,魏晓,和振兴,张波,张国帅
(1.包头北方创业有限责任公司,内蒙古 包头 014040;2.兰州交通大学 机电工程学院,甘肃 兰州 730070)*
城市轨道交通以其特有的快捷方便、节能环保、安全舒适等优势,受到了世界各国的广泛推广[1].但随着城轨交通运营规模的不断扩大,由此引发的振动和噪声问题也变得日见突出,其中轨枕式减振轨道在缓减车轨系统振动方面效果显著[2].轨枕式减振轨道结构其良好的减振性能是由枕下弹性垫板来实现的,因此枕下弹性垫板的力学特性将会直接影响轨道系统的减振效果,进而影响列车运行时的安全性和舒适性.
为了优化弹性垫板的力学性能,国内外学者采用试验研究、数值仿真和理论计算等方式对其进行研究.练松良、肖俊恒等[3-4]采用理论计算和试验研究相结合的方式对传统沟槽型垫板和棱台型垫板的刚度特性进行分析.韦凯、王丰等[5-6]以Vossloh300扣件弹性垫板为研究对象,分析该垫板的黏弹塑性动力特征和在低温条件下的宽频动力特性.王斌仓、翟志浩等[7-9]采用数值仿真的方式对新型轨下网孔式垫板的刚度阻尼特性进行研究,并分析极寒条件对轨下网孔式垫板力学特性的影响.Xiaolin Song[10]基于车辆-轨道耦合动力学理论,研究了轨下垫板刚度变化对车轨动力学参数的影响.罗震、李大成[11-12]研究轨下弹性垫板阻尼参数对车轨系统的影响,研究结果表明:阻尼特性较好的弹性垫层有利于减小轮轨之间的相互作用和轨道结构的振动频率.蔡小培、谭诗宇等[13]建立车辆-有砟轨道-隧道空间耦合动力学模型,对枕下弹性垫层的合理刚度进行探讨.朱超、尤瑞林等[14]总结归纳了国内外常用枕下弹性垫板的连接方式、成形工艺和垫板底面设计的方案.张欢、肖俊恒等[15]等建立无砟轨道动态应力分析模型,分析弹性垫板的刚度特性对轨道板和砂浆疲劳特性的影响,从而确定弹性垫板刚度的合理范围.
目前既有的研究主要是对扣件类垫板和轨枕式减振轨道这个整体进行研究,而单独对枕下弹性垫板力学性能进行分析的相对较少.枕下弹性垫板作为轨枕式减振轨道结构主要的减振元件,可为轨道结构提供必要的减振效果[16],因此对枕下弹性垫板刚度和阻尼特性进行研究十分必要.和振兴、翟婉明等[17]提出了一种网孔结构的弹性垫板,该弹性垫板设有若干个上下贯通的通孔,每个通孔的横截面为蜂窝式正六边形结构,通孔在垫板上呈正交分布,相邻两排通孔交错设置.因此,本文以网孔式结构的枕下弹性垫板为研究对象,基于弹性力学和结构动力学理论,研究枕下网孔式弹性垫板的刚度特性和阻尼特性,并与城轨交通中常用的枕下沟槽型弹性垫板进行对比.
1 研究模型的建立
1.1 枕下网孔式弹性垫板模型的建立
依据文献[18]建立如图1所示的枕下网孔式弹性垫板模型,该垫板长度为650 mm,短边宽度为280 mm,长边宽度为300 mm.弹性垫板采用8节点6面体单元进行网格划分,网格划分类型为C3D8RH.
1.2 材料属性
本文所研究的枕下弹性垫板均由橡胶材料制成,橡胶材料具有超弹特性,材料的应力应变关系呈较强的非线性.Mooney-Rivlin本构模型是最常用的超弹性本构模型,特别在中、小应变的情况下,Mooney-Rivlin本构模型能够较好地反映橡胶材料的应力应变特性,故本次计算采用Mooney-Rivlin本构模型来描述枕下垫板的材料属性.
通过单轴拉伸试验、双轴拉伸试验以及平面剪切试验来获取枕下垫板相应的实验数据,然后采用ABAQUS软件对实验数据进行拟合,可拟合出Mooney-Rivlin本构模型所需的C01和C10,二者分别为0.0149 6 MPa和0.0197 1 MPa.
1.3 边界条件
在实际轨道结构中,枕下弹性垫板位于混凝土轨枕和道床之间,为了简化计算量,分别将轨枕和道床假设成受压刚体和支撑刚体,并采用绑定接触的方式将受压刚体的下表面和枕下弹性垫板的上表面、枕下弹性垫板的下表面和支撑刚体的上表面进行连接,对支撑刚体下表面各个节点的自由度进行约束.
1.4 传统枕下沟槽型弹性垫板模型的建立
为了便于与枕下网孔式弹性垫板进行对比,建立如图2所示的枕下沟槽型弹性垫板.该垫板的整板尺寸、边界条件和材料属性等与枕下网孔式弹性垫板相同.

图2 枕下沟槽型弹性垫板
2 刚度特性
2.1 刚度特性的计算方法
枕下弹性垫板施加的荷载范围应根据垫板的实际受力情况而定,在空载状态下,枕下弹性垫板承受的荷载主要来源于轨枕、扣件以及钢轨等部件的重量,荷载值相应较小,所以设定下限力值为5kN;在有载状态下,枕下弹性垫板主要承受列车的动态荷载,假设列车的静轴重为16t,对应静轮重为80kN,轮重的分配系数和疲劳动载系数分别为0.35和1.3,则枕下弹性垫板的支点压力为80×0.35×1.3=36.4kN,所以设定上限力值为35kN[19];因此对枕下弹性垫板上表面施加40kN的垂向荷载,再按照式(1)来计算枕下弹性垫板的刚度值K.
(1)
式中,F1为对枕下弹性垫板施加的下限荷载,kN;F2为对枕下弹性垫板施加的上限荷载,kN;D1为枕下弹性垫板加载至F1时的位移,mm;D2为枕下弹性垫板加载至F2时的位移,mm;K为枕下弹性垫板的刚度值,kN/mm.
2.2 网孔结构几何参数优化
网孔结构的几何参数如图3所示,网孔内孔径夹角α为内孔径与内壁边长的夹角,网孔外孔径r为垫板上、下表面正六边形内切圆的直径,网孔内孔径b为垫板横截面正六边形内接圆的直径,网孔孔间距d为相邻两网孔之间的间距,弹性垫板厚度h为单个网孔结构的高度.因此,在枕下网孔式弹性垫板整板尺寸和材料属性不变的条件

图3 网孔结构几何参数
下,研究网孔内孔径夹角α、孔间距d以及垫板壁厚h的变化对其刚度特性的影响.
2.2.1 网孔内孔径夹角对刚度特性的影响
当网孔内孔径夹角α在105°~115°的范围内以5°的增量递增时,枕下网孔式弹性垫板刚度值的变化趋势如图4所示,刚度值和最大Mises应力值的计算结果如表1所示.
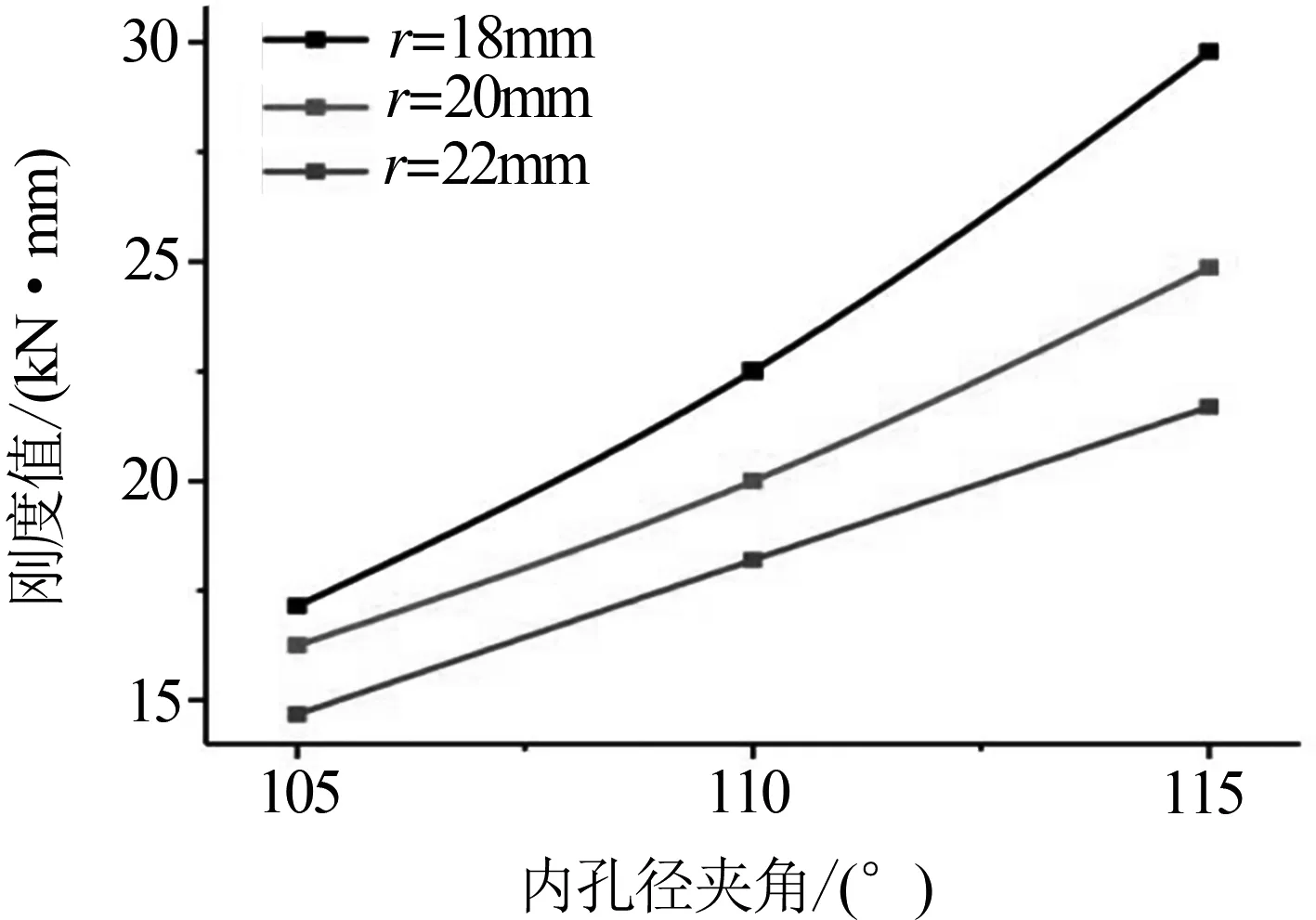
图4 内孔径夹角对垫板刚度值的影响
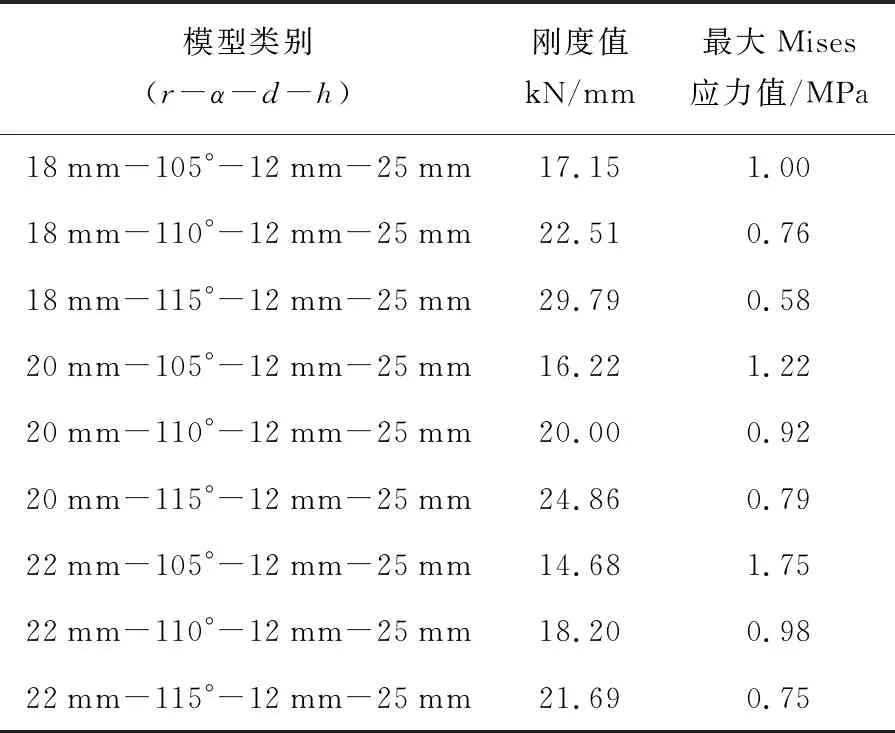
表1 刚度值和最大Mises应力值计算结果(内孔径夹角)
由图4和表1可知:当网孔内孔径夹角α以5°的增量递增时,角度的增大,使网孔内腔的体积减少,垫板的承载力减小,相应的刚度值增大,增大量为26%左右,而垫板的最大Mises应力值将随之减小,减小量为30%左右.
2.2.2 网孔孔间距对刚度特性的影响
当网孔孔间距d在10~14 mm的范围内以2mm的增量递增时,枕下网孔式弹性垫板刚度值的变化趋势如图5所示,刚度值和最大Mises应力值的计算结果如表2所示.
由图5和表2可知:当网孔孔间距d以2 mm的增量递增时,间距的增大,会使承载面的面积增大,由于自由侧面的面积不变,垫板的外形系数将增大,相应的刚度值增大,增大量为11%左右,而垫板的最大Mises应力值将随之减小,减小量为13%左右.

图5 孔间距对垫板刚度值的影响
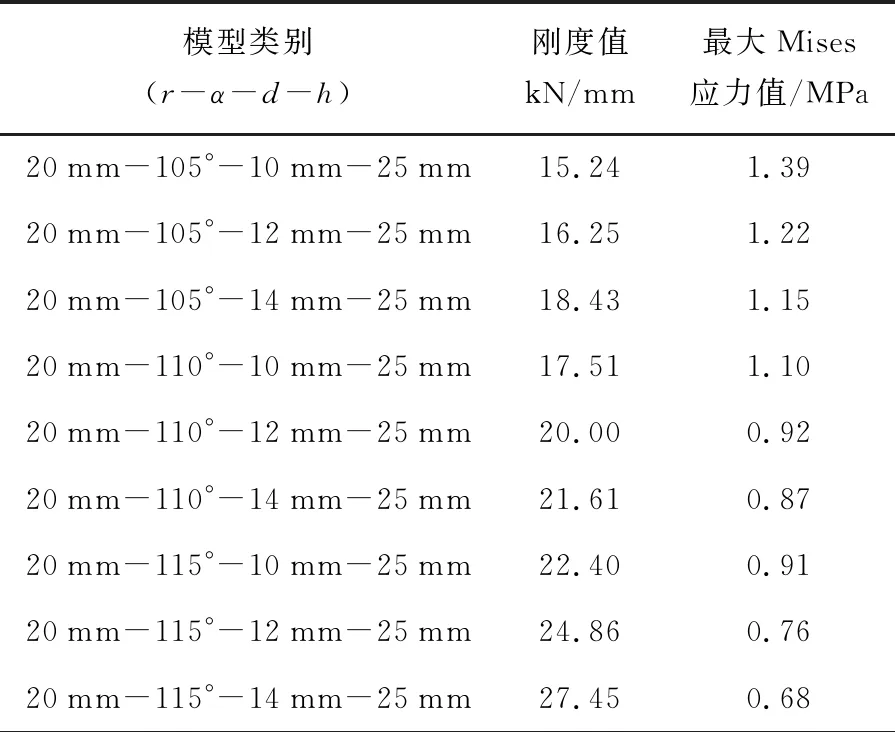
表2 刚度值和最大Mises应力值计算结果(孔间距)
2.2.3 垫板厚度对刚度特性的影响
当垫板厚度h在20~30 mm的范围内以5mm的增量递增时,枕下网孔式弹性垫板刚度值的变化趋势如图6所示,刚度值和最大Mises应力值的计算结果如表3所示.
由图6和表3可知:当垫板厚度h以5 mm的增量递增时,厚度的增加,使自由侧面的面积增大,由于承载面的面积不变,垫板的外形系数将减小,相应的刚度值减小,减小量为21%左右,而垫板的最大Mises应力值将随之减小,减小量为9%左右.

图6 垫板厚度对垫板刚度值的影响

表3 刚度值和最大Mises应力值计算结果(垫板厚度)
2.3 与枕下沟槽型弹性垫板的对比
根据上述所得优化结果,与使用寿命相近的枕下沟槽型弹性垫板进行对比,对比两种枕下垫板刚度值的大小;调整两种枕下弹性垫板的几何参数,使两者刚度值降至13kN/mm左右,来对比两种枕下弹性垫板的最大应力值和应力分布情况.
2.3.1 两种枕下弹性垫板刚度值的对比
将沟槽深度为3 mm、沟槽宽度为5 mm、沟槽间距为15 mm的枕下沟槽型弹性垫板和网孔外孔径为20 mm、内孔径夹角为110°、孔间距为14mm的枕下网孔式弹性垫板进行对比,两种枕下弹性垫板的内部应力云图和荷载-位移响应曲线如图7和图8所示.

图7 两种枕下弹性垫板的内部应力云图

图8 两种枕下弹性垫板的荷载-位移响应曲线
由图7和图8可知:在两种枕下弹性垫板的最大应力值相近的条件下,枕下网孔式弹性垫板的刚度值较小,故其弹性性能更好,更能适用于位移量要求较高的轨道结构.
2.3.2 两种枕下弹性垫板最大应力值的对比
将沟槽深度为6 mm、沟槽宽度为8 mm、沟槽间距为16 mm的枕下沟槽型弹性垫板和网孔外孔径为20 mm、内孔径夹角为105°、孔间距为12mm的枕下网孔式弹性垫板进行对比,两种枕下弹性垫板的荷载-位移响应曲线和内部应力云图如图9和图10所示.

图9 两种枕下弹性垫板的荷载-位移响应曲线

图10 两种枕下弹性垫板的内部应力云图
由图9和图10可知:当两种枕下弹性垫板的静刚度值将至13 kN/mm左右时,枕下沟槽型垫板的最大应力值较大,并且主要承力部位在上下凸台的连接部分,主要承力部位所占面积相对较少,极有可能出现应力集中的现象;而枕下网孔式垫板除了具有最大应力值较小的优势,其主要承力部位在每个网孔结构中,每个网孔结构又在垫板上均匀分布,致使垫板的应力分布均匀.因此,在两种枕下弹性垫板刚度值相近的情况下,枕下网孔式弹性垫板具有最大应力值较小,应力分布较均匀的特点.
3 枕下网孔式弹性垫板的阻尼特性
3.1 阻尼特性的计算方法
阻尼是指振动系统在振动过程中因外界作用或系统自身固有的原因使振动幅度逐渐下降的特性.在结构动力学中,结构阻尼的大小往往通过阻尼比来进行表征,目前常采用对数衰减率法和滞回曲线法这两种方法来计算结构的阻尼比,通过计算所得的阻尼比可了解结构的阻尼特性.
3.1.1 对数衰减率法的计算原理
对数衰减率法的基本思想是根据自由振动衰减的速度来判断结构阻尼比的大小,根据这一原理,定义相隔n个周期的峰值Ak与Ak+n之比的自然对数值为对数衰减率,用λ表示.
(2)
采用对数衰减法计算阻尼比时,不同的n值会对计算结果造成一定的影响,经试验表明,当n的取值使得峰值Ak+n小于Ak的50%时,阻尼比的计算结果较为准确[20].经试算发现当周期间隔为3时,枕下弹性垫板振动衰减波形均满足Ak+3小于Ak的一半.图11为枕下弹性垫板落锤试验的振动波形图.

图11 落锤试验的振动波形图
通过计算所得的对数衰减率λ,可由式(3)来计算出枕下弹性垫板的结构阻尼比ζ[20].
(3)
3.1.2 滞回曲线法的计算原理
滞回曲线是描述力与位移之间关系的曲线,滞回曲线的面积等于内部阻尼所消耗的功,即结构阻尼的大小.基于能量耗散相等原理,在一个振动循

(a) 荷载

(b) 阻尼力
环内实际阻尼所做的功等于实测荷载所做的功,具体计算可由式(4)来描述,模型荷载滞回环面积如图12(a)所示,模型阻尼力滞回环面积如图12(b)所示,两个滞回曲线所包含的面积相等[20].
因此:
SD=ED=πab=πu0(cωu0)
(4)
式中:ED为阻尼力滞回环的面积;SD为荷载滞回环的面积;u0为滞回曲线位移的最大值;ω为外加循环荷载的频率.

(5)
3.2 两种阻尼比算法的对比
将网孔外孔径为20 mm、内孔径夹角为105°、孔间距为12 mm、垫板厚度为30 mm的枕下网孔式弹性垫板作为初始计算模型,分别采用对数衰减率法和滞回曲线法来计算该弹性垫板的阻尼比.
3.2.1 对数衰减率法计算阻尼比
本次计算对枕下网孔式弹性垫板的施加100kN的垂向瞬时荷载,并提取被测垫板前0.25s的时间-幅值响应数据,绘制出枕下网孔式弹性垫板的振动波形图如图13所示.

图13 枕下网孔式弹性垫板的振动波形图
由图13可知:两个波峰幅值分别为1.732和0.861 mm,根据式(2)可计算出枕下网孔式弹性垫板的对数衰减率λ为0.35,将其代入式(3)可计算出枕下网孔式弹性垫板的阻尼比ζ为0.0555.
3.2.2 滞回曲线法计算阻尼比
对枕下弹性垫板的上表面施加20~80 kN的周期性循环荷载,加载频率为5Hz,计算垫板10个周期内的动态特性,并以第三个周期为开始周期,以第八个周期为结束周期,绘制出枕下网孔式弹性垫板6个周期内的滞回曲线图如图14所示.

图14 枕下网孔式弹性垫板的滞回曲线图
由图14可知:滞回曲线的最大位移值约为9.49 mm;滞回环的面积约为270 kN·mm;垫板的动刚度为23.62 kN/mm;系统的固有频率约为13.67 Hz,将所得数据代入式(5)可计算出枕下网孔式弹性垫板的阻尼比ζ为0.055 1.
通过上述对比可知:两种方法所计算出的阻尼比一致性较好,在计算阻尼比时二者可以互相验证;但从计算过程和计算原理来看,对数衰减率法的计算过程更加快捷,计算原理更加简单易懂.
3.3 与枕下沟槽型弹性垫板的对比
在两种枕下弹性垫板刚度值相近的条件下,分别采用对数衰减率法和滞回曲线法来计算网孔外孔径为20 mm、内孔径夹角为105°、孔间距为12 mm、垫板厚度为30 mm的枕下网孔式垫板和沟槽深度为6mm、沟槽宽度为8 mm、沟槽间距为16 mm、垫板厚度为30 mm的枕下沟槽型垫板的阻尼比.
3.3.1 采用对数衰减率法进行对比
对两种枕下垫板进行落锤试验的模拟仿真,可得到两种枕下弹性垫板的时间-幅值响应数据,将其绘制成自由振动衰减波形图如图15所示.

图15 两种枕下弹性垫板的振动波形图
根据式(2)和(3)可计算出两种枕下弹性垫板的对数衰减率和阻尼比,具体计算结果如表4所示.

表4 两种枕下弹性垫板阻尼特性参数对比(对数衰减率法)
与刚度值相近的枕下沟槽型垫板相比,枕下网孔式垫板的振动幅度较大,相应的阻尼比较高,约提高了2.6%左右,因此枕下网孔式弹性垫板衰减自由振动的能力较强.
3.3.2 采用滞回曲线法进行对比
本次计算模拟了两种枕下弹性垫板10个周期内的动态特性,绘制出两者6个周期内的滞回曲线如图16所示.

图16 两种枕下弹性垫板的滞回曲线图
根据式(5)可计算出两种枕下弹性垫板的阻尼比,具体计算结果如表5所示.

表5 两种枕下弹性垫板阻尼特性参数对比(滞回曲线法)
在两种枕下弹性垫板刚度值相近的条件下,枕下网孔式垫板的阻尼比较大,约提高了2.4%左右,
并且网孔垫板的滞回环面积较大,相应的能够吸收较多的冲击能量,缓减轨道结构的振动效应.
4 结论
通过与传统枕下沟槽型弹性垫板的对比,研究了新型枕下网孔式弹性垫板的刚度特性和阻尼特性,研究结论如下:
(1)减小内孔径夹角、减小孔间距以及增大垫板厚度可以有效地降低枕下网孔式弹性垫板的刚度值,因此,在保证垫板强度要求的情况下,可以通过合理地改变网孔几何参数来灵活地调整枕下网孔式弹性垫板的刚度特性,以满足位移量要求不同的轨枕式减振轨道结构;
(2)与传统枕下沟槽型弹性垫板相比,枕下网孔式弹性垫板在提高弹性的同时,可以确保使用寿命变化不大,这样在工程实际应用中可以解决因提高轨道弹性而需经常更换弹性垫层的问题;
(3)对数衰减率法和滞回曲线法所计算出的阻尼比一致性较好,二者可以相互验证,但对数衰减率法具有计算过程更加快捷,计算原理更加简单易懂的特点,因此在两种算法都允许时,优先选择对数衰减率法;
(4)在两种枕下弹性垫板刚度值相近的条件下,枕下网孔式弹性垫板的阻尼比略大,因此在列车动态荷载作用下,采用枕下网孔式弹性垫板的轨枕式减振轨道结构对自由振动的衰减能力较强,可以吸收较多的振动冲击能量.
因此,将枕下网孔式弹性垫板应用于轨道系统中具有可行性,这也为进一步优化轨枕式减振轨道结构的减振特性提供了新方向.
