纵向激励下大跨钢桁拱桥高阶振型效应分析

2022-04-26朱光增厉永旭张永亮朱海龙

兰州交通大学学报 2022年2期

朱光增，厉永旭，张永亮*，季翔，朱海龙

(1. 兰州交通大学土木工程学院，兰州 730070；2. 甘肃交达工程检测科技有限公司，兰州 730070)

在基于位移的结构有限元线弹性分析中，结构响应通常等效为一系列模态响应的叠加[1].由于各阶振型响应对结构总响应贡献不一[2]，为提高计算效率，在满足计算精度的情况下一般会忽略振型贡献较低的振型，由此便涉及评价振型重要性的问题.在国内外抗震设计规范中，Wilson[3]提出的实振型质量参与系数由于概念明确、计算简便而被广泛应用.但是实振型质量参与系数法是以静态基底剪力作为控制目标，计算复杂结构局部动力响应时，极有可能会遗漏对其他结构响应有显著贡献的高阶振型，造成某些地震响应量值偏小[4].另一方面，结构的响应是地震动能量输入下基于结构自振特性的一个能量输出过程.而振型参与质量仅考虑结构自振特性，无法考虑地震动频谱对结构动力响应的影响，对于复杂大跨度拱桥结构，因其结构复杂，构件数量较大，所以地震反应也较为复杂，高阶振型对其地震反应影响显著[5-6].

国内外学者对结构高阶模态效应开展了诸多研究，文献[7-9]以高墩为例进行了高阶振型的定量分析.文献[10]以某主跨(90+180+90) m矮塔斜拉桥为例用平均模态应变能系数对该桥的主导振型进行了识别.文献[11]以大跨网壳结构为例分析了高阶振型对网壳结构的影响.文献[12]以上承式钢桁拱桥为研究对象，通过振型分解反应谱法，分析了主控振型对大跨度钢桁拱桥主拱圈纵向地震反应的影响规律.

从既有文献来看，目前学者对于结构高阶振型的研究大多集中在高墩，对非规则桥梁拱桥的研究较少.文献[12]中以反应谱法计算出拱桥在地震中各阶振型最大响应的最不利组合，计算结果偏大，未能精确考虑拱桥地震过程中的响应历程及地震动对振型贡献的影响.鉴于此，本文以某主跨490 m的上承式钢桁拱桥为研究对象，采用时程分析振型叠加法，分离出各主控振型对大跨度钢桁拱桥的地震反应，并对大跨钢桁拱桥主拱圈高阶振型的贡献规律进行了分析.

1 基于时程分析振型叠加法的各阶模态响应的计算方法

1.1 振型叠加法的基本原理

一致地震激励下线弹性多自由度结构的运动方程由于振型对质量矩阵及刚度矩阵的正交性，以及振型对阻尼矩阵的正交条件假设，可以对其进行解耦，得到各个振型坐标的运动方程如下所示：

(1)

式中：Mj为第j阶振型质量；Cj为第j阶振型阻尼；Kj为第j阶振型刚度；γj为结构的第j阶振型参与系数.γj表达式为

(2)

由以上推导可以看出，采用振型叠加法可以将多自由度动力反应问题转化为一系列单自由度体系的反应问题.对于有上万个自由度的复杂结构，若高阶振型贡献很小，则可以忽略，只计算少量振型，在保证计算精度的前提下大大加快了计算速度[13].

1.2 振型贡献定量指标

本文拟定先根据振型参与质量系数筛选结构整体主要振型，再在其中根据振型内力贡献率确定结构局部区域主要振型.为此定义各阶振型响应为Hn,表达式为

Hn=Nn-Nn-1.

(3)

式中：Nn为结构第n阶地震总反应；Nn-1为第n-1阶地震总反应；ρn为振型贡献率，表达式为

(4)

式中：Hn,max为结构第n阶振型地震反应最大值；Ntot,max为结构地震总反应最大值，各参数示意图如图1所示.

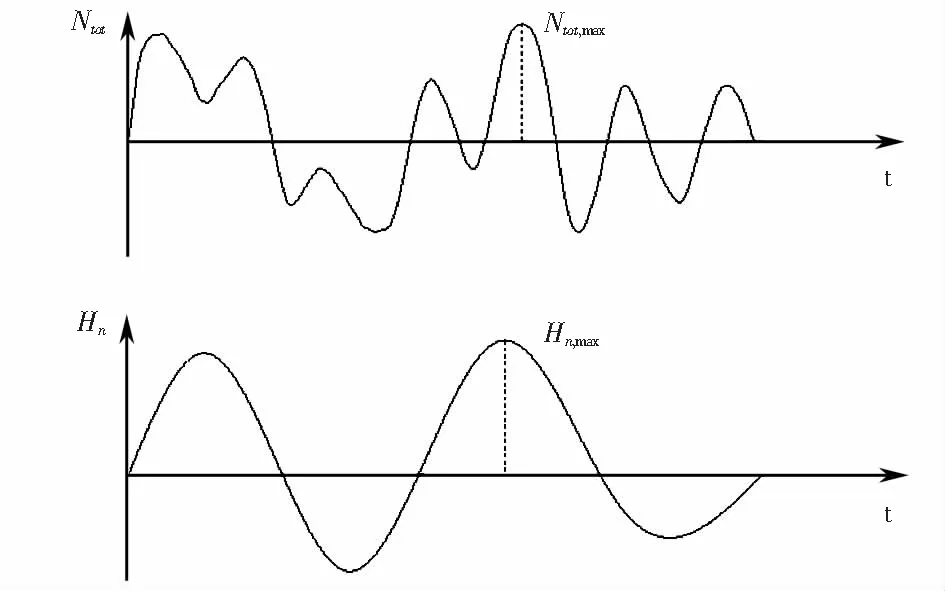
图1 地震总响应与第n阶模态响应示意图Fig.1 Sketch map of total seismic response and the n thorder mode

1.3 主要振型贡献的计算步骤

采用Midas civil建立大跨度钢桁拱桥有限元模型，进行结构动力特性分析，由各阶模态的振型参与质量系数确定主要振型；拟定振型阻尼比为0.03，分别计算拱桥i、i-1阶振型下的地震总反应峰值，并做差求出i阶振型响应峰值；根据确定的主要振型，依次求出每一阶主要振型各个单元最大响应值，计算出各单元主要振型内力贡献率.

2 计算模型介绍

2.1 工程背景

以某跨度为490 m的大跨度上承式铁路钢桁拱桥作为研究对象，桥梁总体布置如图2所示.拱肋内倾3.65°形成提篮拱，主拱圈由4片桁拱组成，每两片组成一肋，两片桁拱间距3.4 m，并通过横杆连成整体[14].拱圈上设置13个立柱，上部梁体为钢箱梁，每侧相邻两钢箱通过正交异性钢桥面板、横梁和横肋形成分离式双主钢箱梁结构形式.根据该桥实地工程地质勘探资料及规范[15]划分，桥址区工程场地类别为Ⅱ类，场地设防烈度为8度，场地特征周期为0.45 s，设计基本加速度为0.248 g.

图2 钢桁拱桥总体布置图(单位：m) Fig.2 General arrangement of steel truss arch bridge (unit:m)

2.2 有限元模型

全桥采用Midas civil建立有限元质点系模型，所有单元均采用空间梁单元进行模拟，拱脚、交界墩底固结，主拱圈与拱上立柱间采用弹性连接-刚性连接，拱上立柱与桥面系采用弹性连接，全桥共计1 037个节点、2 032个单元.将拱桥上弦杆单元沿X方向从左往右依次编号为1至41号，将下弦杆编号为1 000至1 038号，如图3所示.

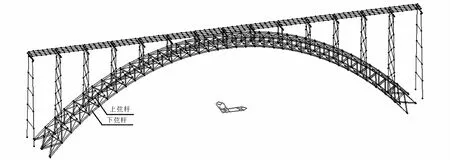
图3 有限元动力计算模型Fig.3 Finite element dynamic calculation model

3 动力特性分析

3.1 桥梁自振特性

对拱桥进行动力特性分析，在振型累计参与质量达到90%所需最少振型中选取单阶振型参与质量大于0.2%的振型，如表1所列.

表1 部分显著贡献模态

由模态分析结果可以看出，拱桥X方向贡献最为显著的模态为第3阶模态，当振型阶数达到161阶时，顺桥向累计振型参与质量达到90%以上.立柱和拱肋振动的振型总共有6阶，累计振型参与质量为57.95%，交界墩振动的振型有5阶，累计振型参与质量为32.78%，由于交界墩振动为自身振动与拱圈及拱上建筑耦合性很小，故可以忽略交界墩振动的振型对拱桥的影响,只考虑立柱及拱肋振动的6阶振型.为简化计算，提高计算效率，在立柱及拱肋振动的3、15、19、20、64、109阶振型中选取单阶振型参与质量大于2%的3、15、20、64阶做为主要考察振型.

3.2 地震动输入

不同的地震波其频谱特性往往不同，所能激发的结构振型也不相同，而结构的响应正是由结构所计算振型响应的叠加，所以不同的地震波则会引起结构不同的响应.规范[16]规定考虑到地震动的随机性，选择的地震加速度时程曲线不应少于3组.为考虑不同地震动对振型贡献的影响，根据该大跨钢桁拱桥场地特征，选取安评波与特征周期相近的EI-centro波、Taft波作为输入，地震波时程曲线如图4所示.反应谱是地震作用的表征，可以直观地分析单自由度结构在不同振型下的最大响应.为此将上述3条地震波转化为阻尼比等于0.03的反应谱曲线，并标出拱桥纵向4阶主要振型的反应谱数值，反应谱如图5所示.

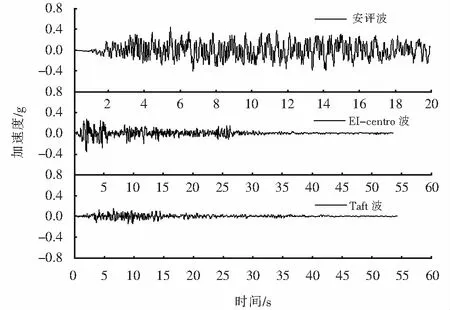
图4 地震波Fig.4 Seismic wave

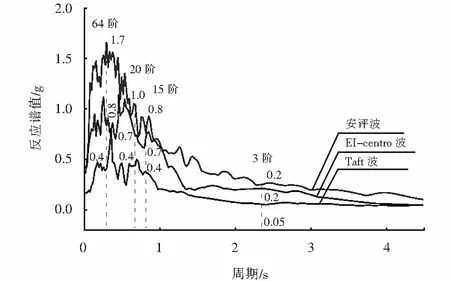
图5 反应谱Fig.5 Response spectrum

4 振型重要性分析

拱桥主拱圈是拱桥的主要承重结构，也是抗震设计的主要关注对象，文献[17]以本桥主拱圈为研究对象，探讨了拱肋上、下弦杆主要内力控制分量，结果表明拱肋上弦杆由弯矩和轴力控制，下弦杆由轴力控制.鉴于此本文主要考察拱肋上弦杆弯矩、轴力和下弦杆轴力中主要振型在总响应中的贡献情况.

在桥墩基底处沿X方向输入地震波，步长取0.02 s，假定振型阻尼比为0.03，分别取前200、300、400阶振型计算拱肋上、下弦杆地震响应.计算得出当计算振型大于200阶时，其地震响应已经趋于稳定，误差较小，因此以300阶振型的计算结果作为精确解，提取主拱圈上弦杆各个单元主要振型轴力、弯矩峰值和下弦杆轴力峰值，将各阶振型响应与拱桥总响应进行对比分析.

4.1 主要振型内力分布特征

以拱顶坐标为原点，沿X方向绘制拱肋上弦杆(坐标：-250～250 m/单元：1～41)、下弦杆(坐标：-250～250 m/单元：1 000～1 038)各阶振型贡献图.为直观分析各阶振型对上、下弦杆地震反应的贡献规律，计算出上、下弦杆各单元主要振型对总响应的占比，绘制为堆积图如图6～14所示.

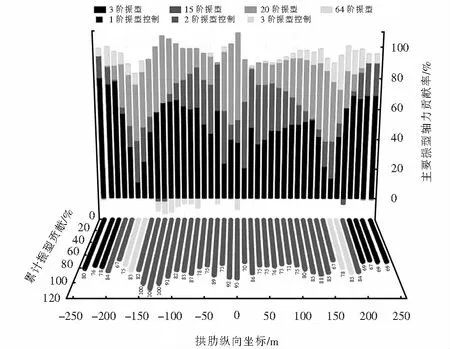
图6 安评波上弦杆轴力贡献率Fig.6 Axial force contribution of the safety evaluation upper chord wave

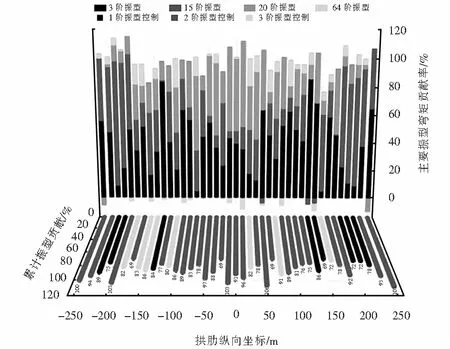
图7 安评波上弦杆弯矩贡献率Fig.7 Bending moment contribution of the safety evaluation of the upper wave chord

图8 EI-centro波上弦杆轴力贡献率Fig.8 Axial force contribution of the EI-centro upper chord wave

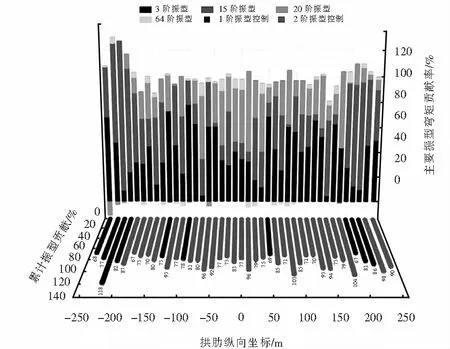
图9 EI-centro波上弦杆弯矩贡献率Fig.9 Bending moment contribution of the EI-centro upper chord wave

图11 Taft波上弦杆弯矩贡献率Fig.11 Bending moment contribution of the Taft wave upper chord

图12 安评波下弦杆轴力贡献率Fig.12 Axial force contribution of the safety evaluation wave lower chord

图13 EI-centro波下弦杆轴力贡献率Fig.13 Axial force contribution of the EI-centro wave lower chord

图14 Taft波下弦杆轴力贡献率Fig.14 Axial force contribution of the Taft wave lower chord

4.2 主要振型内力贡献率指标

4.2.1 振型不同内力分量差异指标

为便于分析主拱圈上、下弦杆不同内力分量主要振型贡献规律，引入振型内力贡献率差值λ

(5)

式中：n为计算单元的个数；ρi,N、ρi,M分别为计算单元的振型轴力、弯矩贡献率.绘制3条地震动激励下拱肋上弦杆主要振型轴力与弯矩贡献率差值的绝对值如图15所示.

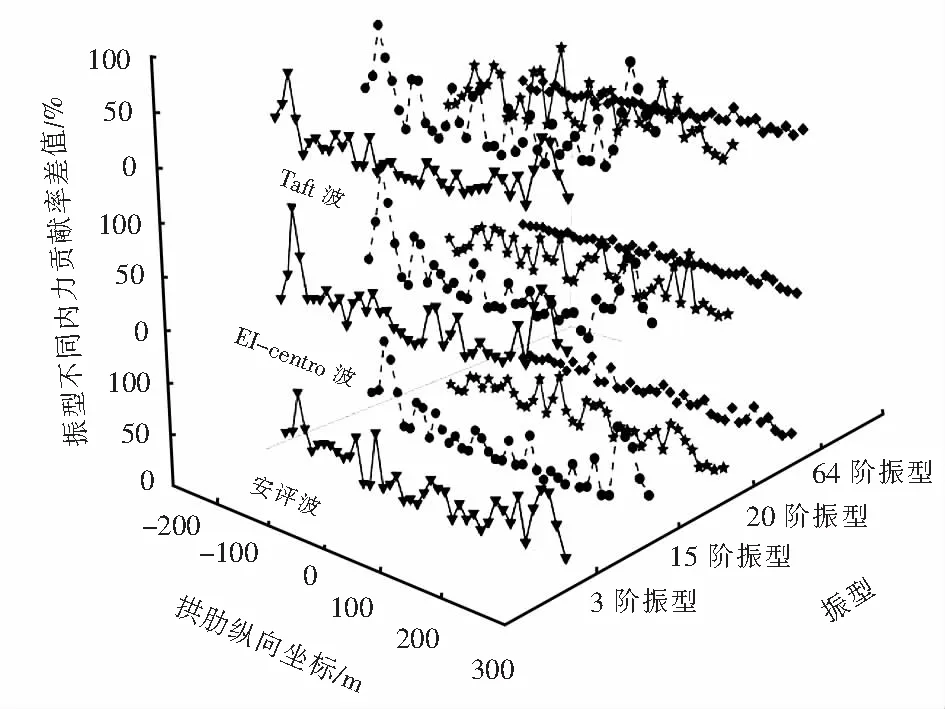
图15 主要振型不同内力贡献率差值Fig.15 Difference of internal force contribution rate of main vibration mode

4.2.2 控制振型阶数指标

我国规范[16]规定:对于墩高超过40 m、墩身一阶振型有效质量低于60%的桥梁需进行专门研究.鉴于此，本文以拱肋上、下弦杆各单元总响应的2/3作为控制指标，若有1阶振型贡献大于总响应的2/3,则认为该单元为1阶振型控制，除1阶振型控制单元外，若有2阶振型响应和大于总响应的2/3,则认为该单元为2阶振型控制，以此类推将拱肋上、下弦杆划分为在1～3阶振型控制区域.3条地震波激励下拱桥上、下弦杆不同内力分量的控制振型单元个数如表2所列.

表2 控制振型阶数分布图

1) 大跨度钢桁拱桥，由于结构复杂，振型众多，不同于以往的单阶振型主控，局部区域总响应呈现出多阶振型共同控制的现象.例如拱桥上弦杆轴力贡献图中1阶振型控制单元数为25个，2、3阶振型控制单元数为98个；拱桥上弦杆弯矩贡献图中1阶振型控制单元数为34个，2、3阶振型控制单元数为89个；拱桥下弦杆轴力贡献图中1阶振型控制单元数为46个，2、3阶振型控制单元数为71个.下弦杆轴力单阶控制振型单元个数要多于上弦杆.

2) 拱桥上弦杆同一区域，同一阶振型贡献率因内力分量的不同而不同.由图15可以看出，从拱桥上弦杆部位来看，上弦杆拱脚区域不同内力分量下振型贡献差异最大，最大值为EI-centro波第15阶振型3号单元(-250～-200 m)114%.从加载的地震动来看，3条地震波激励下拱桥上弦杆同一阶振型不同内力分量贡献率均不相同，但差异不大.安评波上弦杆振型内力贡献差值λ为18%，最大差值为3号单元(-250～200 m)15阶振型88%；EI-centro波上弦杆振型内力贡献差值λ为20%，最大差值为3号单元15阶振型114%；Taft波上弦杆振型内力贡献差值λ为21%，最大差值为38号单元(-250～-200 m)15阶振型106%.

3) 拱桥上、下弦杆同一阶振型贡献率因区域不同而不同.从单个图来看，以图7为例，各阶振型贡献率在各个单元均不相同，差异最大单元为3阶振型的1号(-250～-200 m)与6号(-200～-150 m)，差值69%.从拱桥上、下弦杆对比来看，以图7、13为例，在拱肋-150～150 m区段内，下弦杆3阶振型轴力贡献率明显大于上弦杆3阶振型轴力贡献率，差异最大单元为上弦杆24号(0～50 m)与下弦杆1 023号(0～50 m)单元的3阶振型贡献率，差异值为75%.

4) 地震动的输入对振型贡献率也存在影响.在3条地震波激励下,对比安评波、EI-centro波结果，可以明显看出Taft波第3阶振型贡献减小.由图5反应谱可以看出，安评波、EI-centro波第3阶振型响应为第15阶振型响应的1/4、2/7，而Taft波第3阶振型响应为0.05 g，是第15阶振型响应的1/8,远远小于其他主要振型响应，这直接导致了第3阶振型贡献率的减小.

5) 振型参与质量系数是一个整体性指标，与主要振型间存在定性的正相关关系，但对于拱桥局部区域，振型参与质量最大的振型其内力贡献不一定最大.如拱桥振型参与质量最大的振型阶数为第3阶振型，但在拱肋上弦杆弯矩贡献图的拱脚区域，均出现15阶振型贡献率大于3阶振型的情况.图8中拱脚区域37号(200～250 m)单元15阶振型贡献率最大为78%；图10中拱脚区域3号(-250～-200 m)单元15阶振型贡献率最大为118%；图12中拱脚区域37号(200～250 m)单元15阶振型贡献率最大为105%.