基于CEEMD和快速谱峭度图的地铁轴箱轴承故障诊断

戎芳明,贾小平,杨陈

(中车浦镇车辆有限公司 转向架研发部，江苏 南京 210000)*

转向架轴箱轴承是影响城轨车辆的行车安全的重要部件，如何对其进行智能诊断是一个值得研究的课题.传统频域分析法主要是通过观察频谱图中故障特征频率处有无谱峰来诊断故障，诊断效率和精度都较低.近年来，随着EMD、EEMD、VMD等理论在智能故障识别领域的应用，轴承故障诊断的手段进一步丰富.但EMD分解会出现模态混叠现象，EEMD可能会引入新的重构误差，为避免EMD的模态混叠和EEMD重构误差等问题，本文提出了基于CEEMD和快速谱峭度图的故障诊断方法.通过仿真、试验和工程实践都表明，该方法有效识别出转向架滚动轴承故障，为轴承故障诊断的智能化提供了新思路[1].

1 CEEMD-FSK算法基本原理

1.1 EMD、EEMD和CEEMD算法原理

经验模态分解(Empirical Mode Decomposition)，即EMD方法，是一种自适应的数据处理方法，使复杂信号分解成若干个本征模函数分量(IMF分量)来组成，但得到的IMF分量往往存在模态混合，建立式(1)仿真信号数学模型，如图1可明显可以看出IMF1中包含不同频率分量[2].

(1)

图1 EMD方法分解信号实例

为解决EMD分解出现的模态混叠现象，通过加入白噪声，衍生出EEMD方法，而通过成对添加符号相反的白噪声信号到原始信号，改进为CEEMD方法，其仿真时域波形处理步骤如图2.

图2 CEEMD方法的分解流程图

1.2 快速谱峭度图法与改进型共振解调法

1.2.1 快速谱峭度图

谱峭度法(Spectral Kurtosis，SK)，通过计算信号峭度值来指出隐藏的非平稳信号出现的频带范围，本文采用二分法分解的快速谱峭度图法以确定各IMF信号的带通滤波频率范围.同时结合互相关系数的方式，有效选出关键IMF分量. 定义系统激励信号x(t),其响应为Y(t)，H(t,f)为Y(t)在频率f处的复包络.

(2)

谱峭度的定义为四阶归一化累积量，用式(3)表达：

(3)

其中，含噪声的故障振动信号Z(t) 的谱峭度定义为：

(4)

式中，KY(f)为故障振动信号Y(t)的谱峭度，ρ(f)为信噪比的倒数.

1.2.2 改进型共振解调法

共振解调法，又称包络分析法，流程图如下图3所示.针对轴承振动信号，针对轴承振动信号，一般采取希尔伯特变换(Hilbert)进行求解，本文对比了传统包络谱、平方包络谱和多次方包络谱求解结果，结果表明采取平方包络谱的方法更有利于特征信号的识别[1,3].

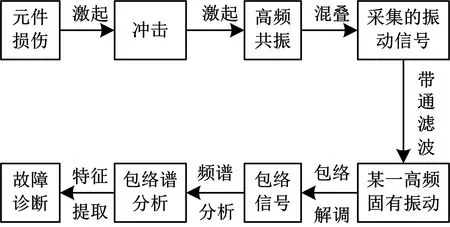
图3 共振解调法的流程图

1.2.3 CEEMD-FSK算法流程

原信号通过CEEMD分解成多个IMF，分别计算原始信号和各个IMF的快速谱峭度图，从各个快速谱峭度图中找出颜色最深的色块，即谱峭度最大值区域，判断各个IMF谱峭度最大值所处频带区间与原信号频带区间是否相一致，若一致，则初步认为则该IMF为关键IMF，否则去除.然后分别选取各IMF与原信号相关系数较大且其峭度值都大于3.5的前N阶(N≤5)IMF信号，将选取的IMF进行信号重构.再对重构信号进行快速谱峭度分析，确定带通滤波频率范围，然后通过改进型共振解调处理进行轴承故障诊断[4-6].将这种基于CEEMD和快速谱峭度图(Fast Spectral Kurtosis Diagram，FSK)的方法称为CEEMD-FSK算法，具体算法流程如图4所示.

图4 基于CEEMD-FSK算法的轴承故障诊断流程图

2 仿真信号分析与对比

2.1 仿真信号模型的构建

为验证本文方法的高效性，提出以下轴承故障信号仿真模型，假设如下：

(5)

其中，s(t)为周期性冲击成分，幅值A0=0.5，转频fr=50 Hz，衰减系数C=900，共振频率fn=3 500 Hz.内圈故障特征频率fi=160 Hz，n1(t)和n2(t)为高斯白噪声，其信噪比设置为-3.

图5 基于EMD方法进行仿真模型故障诊断

EMD-包络谱方法诊断结果如图5，未找到轴承故障特征信号，可见该方法对复杂轴承故障信号诊断的有效性较低，需进一步优化.

2.2 CEEMD-FSK方法的故障特征诊断

使用CEEMD-FSK方法对仿真模型信号分析，由图6可知，得共振频率段范围为(3 000 Hz，4500Hz)，这是完全符合共振频率fn=3 500 Hz的设置.由图7可知，能够诊断出基频信号和内圈故障信号，很接近转频fr=50 Hz 和内圈故障特征频率fi=160 Hz 的设置，由此可说明，CEEMD-FSK方法在复杂轴承信号下能高效检测到轴承故障特征信息[7].

图6 仿真模型信号的快速谱峭度图

图7 基于CEEMD-FSK方法的仿真模型故障特征诊断

3 振动测试分析和试验对比

为验证本文方法的有效性，将该方法用于某城轨车辆轴箱轴承的前期故障诊断中.

3.1 滚动轴承已知参数

轴承型号：BC2-0111;滚动体个数：16;滚动体直径：27 mm;滚道节径：167.5 mm;接触角：0°;转速为252 r/min(4.2 Hz)时对应车速40 km /h.

根据滚动轴承故障频率的计算公式和实际滚动轴承参数，得各故障特征频率分别为内圈：39.02Hz、；外圈：28.18 Hz；滚动体：25.38 Hz；保持架：1.76 Hz.

3.2 实测故障信号采集与分析

试验主要仪器和传感器如下：数据采集分析仪为INV3062T0；加速度传感器(50g)为INV9832; DASP智能数据采集和信号分析系统V10为DASP-V10工程版平台软件；笔记本电脑Lenovo T440.

针对某地铁车辆，在空车状态下运行速度为40 km/h的某节车厢转向架各轴箱轴承进行振动信号采集，采样频率设为19 692.3 Hz，车辆稳定运行状态下采集时间长度为200 s，测点位置为各轴箱体正上方.

3.3 实测数据分析与拆装检测对比

3.3.1 信号的重构和故障诊断

通过快速谱峭度图和相关系数综合选择出前5阶IMF，具体排序见图8.对信号进行重构，再次通过快速谱峭度图，确定带通滤波参数为(2000Hz，3 000 Hz).

图8 选取前出前5阶IMF作为重构信号

对重构信号进行带通处理后，采用平方包络谱方法进行共振解调，由图9可知该轴承实际转频为4.66Hz，存在轴承内圈故障特征信号42.71Hz，而且出现了38.2 Hz的边带信号，对比各特征故障频率，可诊断该轴承存在内圈故障.

图9 基于CEEMD-FSK方法的轴箱轴承信号故障特征诊断

3.3.2 诊断结果与拆装对比

为检测CEEMD-FSK方法诊断结果的准确性， 将目标轴箱轴承拆装送检， 具体结果如图10所示，对比图9诊断结论，可以说明该方法的有效性和实用性.

图10 故障轴承检测示意测点及实际状态

4 结论

本文基于CEEMD和快速谱峭度图选取关键IMF分量进行信号重构，再通过快速谱峭度图确定滤波频带，利用共振解调技术提取平方包络谱判断滚动轴承故障类型.该方法改进了传统EMD-包络谱方法的不足，提高了计算效率，诊断结果更精确，同时快速谱峭度图克服了主观上确定滤波参数的不确定性.仿真分析和试验结果都表明了该方法能有效和正确地选择敏感分量，提取到滚动轴承早期微弱故障特征信号，有效诊断出轴箱轴承故障类型.