膨胀土地基中单桩受扭非线性分析

江 杰，王顺苇，欧孝夺，王 智，杨 迪

(1. 广西大学土木建筑工程学院，广西，南宁 530004；2. 工程防灾与结构安全教育部重点实验室，广西，南宁 530004；3. 广西防灾减灾与工程安全重点实验室，广西，南宁 530004；4. 中铁建设集团有限公司，北京 100040)

膨胀土在全球40 多个国家均有分布，范围十分广泛，在我国主要分布在云南、广西、四川等10 多个省份[1]。其胀缩特性是造成地基上方建(构)筑物发生倾斜、变形、不均匀沉降的的重要因素，具有十分突出的工程问题[2]。为了保证膨胀土地区建(构)筑物的安全，实际工程中往往采用桩基础形式。大型广告牌、风力发电塔以及弯梁桥在不均匀水平力的作用下，会对其桩基础产生扭矩[3 − 7]，当竖向荷载较小时，扭矩将会成为桩身承载力的控制性因素，在设计中若忽略扭矩的作用，可能会造成重大的工程损失[8]。膨胀土浸水后会对桩基础产生轴向拉力作用[1, 9]，而研究表明轴向力的存在会使单桩扭矩承载力降低[10 − 12]，因此有必要对膨胀土地基中的受扭单桩进行进一步的研究，为工程设计提供参考。

国内外学者对膨胀土地区竖向和水平荷载作用下单桩的承载特性进行了相关研究[13 − 19]，对于受扭单桩，Stoll[20]在砂土中对钢管桩回填混凝土首次对单桩进行了扭矩加载试验，得到了桩顶扭矩和扭转角的关系曲线，为后续研究奠定了基础；Poulos[21]基于弹性连续介质理论求解出了桩顶扭矩和扭转角的关系，并在粘性土中进行了验证；Zhang 等[22]利用力学的变分原理推导出了桩的控制微分方程，通过迭代法求解出了桩顶扭矩和扭转角的关系，并在砂土和黏土地基中进行了验证；邹新军等[4]结合平衡原理和剪切位移法求得了砂土中单桩受扭的弹塑性解；赵明华等[23]假设桩为弹性梁，采用非线性弹簧模拟桩土间的相互作用关系，建立了粉土地基中受扭单桩的简化计算模型；Basack 等[24]采用边界元法求得砂土地基中单桩在扭矩作用下的数值解；Li 等[25]利用现有的界面剪切试验建立荷载传递模型，采用有限差分法，得到单桩受扭的非线性计算方法。

综上所述：目前国内外学者主要针对砂土、黏土和粉土地基中的受扭单桩进行了研究，对于膨胀土地区受扭单桩的研究较少。膨胀土浸水后桩身轴力的存在，使得常规的单桩受扭计算理论会过高的估计承载力，偏于不安全。鉴于此，本文对膨胀土浸水后桩侧竖向摩阻力的分布模式进行了探讨，在此基础上求出膨胀土地基浸水后受扭单桩的非线性解，通过膨胀土地基中单桩模型试验，对理论进行了验证，并对浸水前后单桩扭转承载特性以及不同膨胀率的膨胀土浸水对基桩的受力和变形的影响进行了分析。

1 计算模型及假定

本文的分析基于以下假定：

1)桩为线弹性等截面桩。

2)定义被浸润的膨胀土层厚度为“膨胀影响深度”；假设膨胀影响深度内的膨胀土隆起量随深度线性变化[15]，膨胀影响深度以下的隆起量为0，计算公式如下：

式中：ws(z)为深度z处的膨胀土隆起量；h0为膨胀影响深度；ws0为膨胀的土地表膨胀量。

3)膨胀土浸水会对桩身产生上拔力，在桩身中性点(桩土相对位移为0 处)以上对桩身作用竖直向上的摩阻力，在中性点下对桩身作用竖直向下的摩阻力。因此可假设膨胀土浸水时的桩-土界面模型如图1 所示，浸水过程中桩-土界面竖向正、负摩阻力以及扭矩作用下的桩身环向摩阻力(s(z)≥0段)均符合Kraft 等[26]提出的荷载传递函数形式。

图1 膨胀土浸水条件下桩-土界面模型Fig. 1 Load-transfer model for pile-soil interaction under expansive soil swelling

式 中：s(z)为 桩-土 相 对 位 移s(z) =w(z)−ws(z)；ws(z)为桩所处位置深度z处的膨胀土浸水后的隆起量；Gs为土体小应变时的初始剪切模量；ψ=τ(z)Rf/τf，Rf为应力-应变曲线拟合常数，可取0.9～1.0；τf为桩侧极限摩阻力；r0为桩截面半径；rm为有效影响半径。

2 理论分析及推导

2.1 环向极限摩阻力的确定

浸水后对桩顶施加扭矩作用，桩侧土体对桩身产生环向的摩阻力，桩侧竖向及环向摩阻力共同作用于桩身。如图2 所示，采用边界元法将桩纵向离散为n个长度为L/n的单元，第i单元的桩侧竖向和环向摩阻力分别为τv(i)和τt(i)，假设两者共同作用下的桩侧合摩阻力τ(i)不大于极限摩阻力τf(i)，可得到：

图2 浸水后单桩边界元离散示意图Fig. 2 Boundary element discretization of pile after immersion

式 中：τf(i) 为 第i单 元 的 极 限 摩 阻力；τtf(i)为 第i单元环向极限摩阻力。

由式(4)可知要想得到环向的极限摩阻力，须先求出单桩浸水后的竖向摩阻力。

2.2 浸水作用下单桩竖向摩阻力 τv(i)的求解

式(14)的求解过程如下：① 假设沿桩身节点位移w=0，由桩侧土体自由位移场ws(z)求桩土相对位移s(z)=w(z)−ws(z)，进而求出桩身节点切线刚度；② 由式(14)求出沿桩身节点的位移wk；③ 用新求出的桩身节点位移wk求出桩-土相对位移和桩侧土体的切线刚度。利用新的割线刚度求出新的桩身节点位移wk+1；④ 取|wk+1−wk|作为迭代控制误差，若误差大于限定值则重复②～④直至迭代误差小于限定值。

由以上数值解求出桩土相对位移，结合式(2)即可求出桩身单元竖向摩阻力。

2.3 浸水作用下单桩受扭非线性计算

为得到每个桩单元的桩侧环向摩阻力，采用中心差分法将桩长离散成n个相等的单元，并在桩顶和桩端各增加一个虚拟等分节点，并代入桩端和桩顶边界条件对式(18)进行差分离散，可以得到方程组：

式(24)的求解过程如下：① 假设沿桩身节点的扭转角θ 为任意非零矩阵，由式(17)求得深度z处的相对扭转位移st(z) ，将st(z)代入式(2)求出τt(z) ，由 式(4)求 出τtf(z) ，若τt(z)≥τtf(z)，则 取τt(z)=τtf(z) ，由式(9)求出kθ(z) ，进而得到Kt′；② 由式(24)求出沿桩身节点的扭转角θk；③ 用新求出的桩身节点扭转角θk求出桩身扭转刚度矩阵Kt′k；利用新求出的桩身扭转刚度矩阵Kt′k求出新的桩身节点扭转角θk+1；④ 取|θk+1−θk|作为迭代控制误差，若误差大于限定值则重复②～④直至迭代误差小于限定值。

3 方法验证与分析

通过试验分别对桩侧竖向摩阻力τv(i)和环向摩阻力τt(i)的求解进行验证，在此基础上将浸水条件下单桩受扭的求解与本文的试验结果与进行对比分析。

3.1 试验及测量装置

采用自主研制的桩基加载装置，对膨胀土地基中的单桩进行浸水前后的室内静载模型试验，加载装置如图3 所示。试验装置主要分为三个部分：模型箱、加载装置和浸水装置。模型箱尺寸为1 m×1 m×1 m。加载装置由加载架、滑轮和力臂组成。浸水装置由竖向浸水管和水桶组成，模型箱底部填筑约250 mm 厚的砂砾层，浸水管插入砂砾层。通过水管将模型箱底部和水桶连接，利用虹吸原理对水桶注水，以保持水平面与土表面高程一致，实现对膨胀土的全浸水膨胀。

图3 加载装置示意图Fig. 3 Schematic of loading device

在膨胀土地基表面设置百分表测量地表隆起量，通过固定于桩顶的量角器测量桩顶扭转角，在桩顶设置一个长为0.1 m 的力臂，通过定滑轮对力臂施加水平力，使其转化为扭矩，两个定滑轮的摩擦系数μ1和μ2分别为0.943 和0.914，桩顶扭矩可通过下式确定：

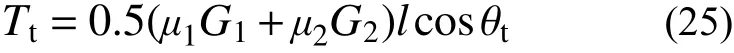
式中：G1和G2分别为两端重物的重量； θt为测得的桩顶扭转角，为方便计量，本试验采用水来代替重物。

通过应变片测量桩身切应变和轴向应变，桩身扭矩和轴力分别由式(25)、式(26)确定：

式中：桩身剪切模量Gp=Ep/(2(1+ν))；桩身泊松比ν取值为0.3； γ为桩身切应变； ρ为应变片距中性轴的距离；Ep为桩身弹性模量； ε为桩身轴向应变。

3.2 模型桩

采用铝合金空心管制作单桩模型，弹性模量69.7 GPa，长800 mm，埋入膨胀土650 mm，直径25 mm，壁厚2 mm。在模型桩内表面每隔100 mm设置一组测点，每组测点设置一个BF350–3AA和BHF350-3HA 型应变片分别测量桩身轴向应变和切应变，最后一组应变片设置在桩端以上5 mm处，共设7 组测点，通过TST3822EN 静态应变测试仪采集应变。桩端采用尼龙塞进行粘贴封底，待模型箱内土体填置100 mm 之后将模型桩垂直插入土体，土体填筑过程中不断测量模型桩与模型箱之间的距离，对桩实时进行纠偏，保持其竖直。

3.3 土体参数

试验用膨胀土取自广西南宁水牛研究所附近的灰白色膨胀土，其自由膨胀率为65.5%，属于中等膨胀土，基本物理力学性质如表1 所示。土料经过烘干、粉碎，制成初始含水量为20%的土样。土样采用人工夯实进行分层填筑，每层控制夯实后的厚度为100 mm，填土总高度为700 mm，填筑土层干密度为1.46 g/cm3。

表1 膨胀土基本物理力学性质Table 1 Physical and mechanical properties of expansive soil

3.4 试验方案

为了研究膨胀土浸水对单桩扭转承载特性的影响，共设计3 组试验，第1 组测量浸水后的桩身轴向应变；第2、3 组分别测量浸水前后，不同的桩顶扭矩作用下的桩身切应变和桩顶扭转角，具体如表2 所示。

表2 试验加载方案及测量数据Table 2 Test loading scheme and measurement data

试验采用分级的方式加载，每级加载增量为预计极限荷载的1/10，当桩顶扭矩-扭转角曲线(T～θ 曲线)出现突变时加载结束。对于浸水前的模型桩，夯土结束后即可进行加载试验，对于浸水后的模型桩，浸水完成后即可进行加载试验。当百分表读数与应变仪数据趋于稳定后48 h内再无明显波动，则浸水试验完成。本次试验浸水历时14 d，地表隆起0.011 m。试验装置如图4所示。

图4 模型桩加载试验装置Fig. 4 Loading test device of model pile

3.5 试验结果与分析

1)浸水后桩侧竖向摩阻力分布

通过第1 组试验测得的桩身轴向应变求出桩身轴力，利用式(5)对桩身轴力数据进行处理得到桩身竖向摩阻力，图5 为浸水完成后桩身竖向摩阻力分布图，图中竖向摩阻力向上为正，由图5可知，桩侧竖向摩阻力呈现出先增大再减小然后反向增大的特点。大约在桩深为0.4 m 以上部分的膨胀土对桩产生向上的上拔力，摩阻力为正值；0.4 m以下部分的膨胀土对桩作用向下的拉力，阻碍单桩的抬升，摩阻力为负值。即未施加桩顶扭矩时，中性点位置约在桩的中下部0.4 m 处，与张大峰[1]的结论相似，计算结果和试验数据相比最大误差为2.8%相差较小，验证了本文竖向摩阻力的计算方法。

图5 桩身竖向摩阻力分布Fig. 5 Vertical frictional resistance distribution of pile shaft

2)浸水后桩侧环向摩阻力分布

对桩顶施加扭矩之后，桩-土界面之间会产生环向相对位移，从而产生了环向摩阻力，为验证本文环向摩阻力计算的正确性，分别提取第2 组试验中桩顶扭矩为1.5 N·m、3.0 N·m、4.5 N·m、6.0 N·m 所对应的桩身切应变数据，并求出桩身扭矩，利用式(15)对桩身扭矩数据进行处理得到桩身环向摩阻力，计算结果与试验数据对比如图6所示，4 组数据与试验结果均比较接近，证明了环向摩阻力计算的正确性。

图6 浸水后桩侧环向摩阻力分布Fig. 6 Distribution of lateral circular friction after immersion

由图6 可知：在0 m～0.15 m 范围，由于桩土竖向相对位移较大，桩-土界面已经进入塑性阶段，导致桩侧环向摩阻力较小；在0.15 m～0.25 m深度范围，桩-土界面处于弹塑性状态，桩侧环向摩阻力快速增加；在0.25 m 深度以下，当桩顶扭矩为1.5 N·m 和3.0 N·m 时，由于桩-土界面相对位移较小尚处于处于弹性状态，环向摩阻力几乎没有变化，当桩顶扭矩增加到4.5 N·m 和6 N·m时，桩-土界面渐渐进入塑性阶段，由于土体的抗力作用越来越明显，环向摩阻力也在增加，呈现出非线性的变化。

3)浸水前后荷载位移对比分析

对于浸水前单桩，只需令竖向摩阻力为0 ，引入Poulos[21]提出的桩端边界条件进行计算，即可得到T-θ 曲线。将本文计算得到的T-θ 曲线与试验数据进行对比，如图7 所示，当桩顶扭矩较大时本文计算方法和试验结果均较为吻合，但当荷载较小时误差较大，原因是试验过程中当桩顶扭矩较小时，桩顶扭转角并没有明显的变化，导致观测结果存在一定的误差。但整体来看本文计算得到的T-θ 曲线和试验数据较为吻合，证明本文提出的膨胀土地基浸水后单桩受扭非线性计算方法的正确性。此外还可看出，浸水前后单桩的极限扭矩分别为19.82 N·m 和6.88 N·m，即浸水后单桩的极限扭矩降低了65%。

图7 浸水前后T～θ 曲线对比Fig. 7 Comparison of T～θ curves before and after immersion

分别提取第2、3 组试验中桩顶扭矩为2 N·m和4 N·m 时桩身扭矩试验数据与计算数据进行对比，如图8 所示：浸水前后的桩身扭矩分布计算结果与试验数据相比趋势均一致且误差较小，浸水前桩身的扭矩近似线性分布，与文献[4]趋势一致，再次证明了本文计算方法的正确性。浸水后单桩的桩身扭矩分布呈现出非线性变化的规律，在深度为0 m～0.25 m 范围，桩身扭矩变化幅度较小，是由于在施加扭矩之前，此深度范围内膨胀土的膨胀作用导致桩土竖向剪切位移较大，桩-土界面已经发生了滑移(简称“滑移段”)，从而使环向摩阻力的作用不明显，导致桩身扭矩的增量较小；在0.25 m 深度以下，桩身扭矩呈现出近似线性快速减小的特点，究其原因，桩土竖向相对位移较小，桩-土界面尚未发生滑移(简称“未滑移段”)，环向摩阻力有较大的发挥空间，土体作用的环向摩阻力使桩身扭矩快速减小。此外还可以看出当桩顶扭矩相同时，浸水前后的桩身扭矩分布有着较大的差异，在实际工程中可根据桩身扭矩分布特点进行合理配筋。

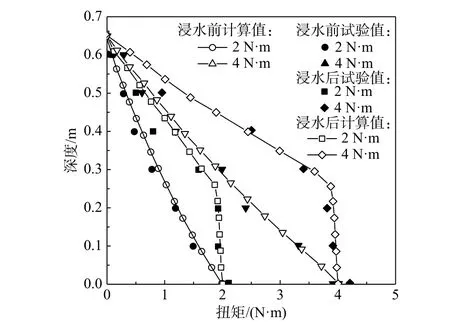
图8 浸水前后桩身扭矩分布情况Fig. 8 Distribution of pile torque before and after immersion

4)膨胀率的影响

为研究不同膨胀率的膨胀土浸水后对单桩T～θ 曲线的影响，设不同膨胀率的膨胀土对应的地表隆起高度为0.004 m～0.016 m，由图9 可知：随着膨胀率的增加，单桩的极限扭矩依次降低，且降低的幅度越来越小；当桩顶扭矩为定值时，随着膨胀土膨胀率的增加，桩顶扭转角增加的幅度越来越大，桩-土体系的加载刚度降低的幅度越来越大。因此，地表隆起会造成桩-土体系加载刚度和极限扭矩大幅度降低，且膨胀土的膨胀率越高，单桩抗扭能力和桩-土体系加载刚度降低的幅度越大。

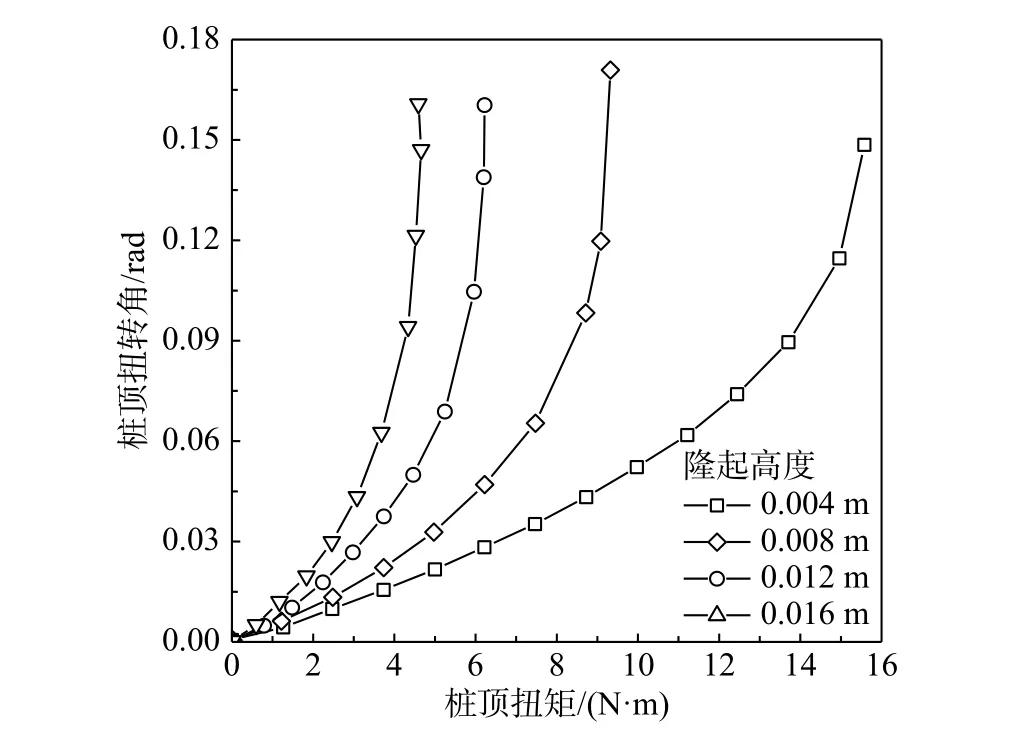
图9 不同膨胀率的膨胀土对应的T～θ 曲线Fig. 9 T～θ curve corresponding to expansive soil with different expansion rates

图10 为桩顶扭矩为4.5 N·m 时不同膨胀率的膨胀土对应的桩身扭矩分布情况，假设不同膨胀率的膨胀土对应的地表隆起高度同上，由图10 可知，膨胀率对桩身扭矩的分布有着重要的影响，随着膨胀率的增加“滑移段”的长度也在增加。

图10 不同膨胀率的膨胀土对应的桩身扭矩Fig. 10 Pile shaft torque corresponding to expansive soil withdifferent expansion rates

4 结论

为探讨膨胀土地基中受扭单桩的承载特性，考虑膨胀土浸水隆起对桩侧摩阻力及桩端边界条件的影响，采用有限差分法和边界元法，对桩身的内力进行了分析，主要结论如下：

(1)提出了膨胀土地基浸水后单桩桩侧竖向摩阻力的计算方法，在此基础上，结合边界元法提出了膨胀土地基浸水后单桩受扭的非线性分析方法，并通过单桩模型试验进行验证，结果较为吻合。

(2)桩侧竖向摩阻力沿桩身先增大后减小，随后反向增大，中性点位于桩身的中下部；桩侧环向摩阻力在桩身中上部接近于0，然后沿桩身快速增加，达到峰值之后，当桩-土界面处于弹性状态时趋于稳定，处于塑性状态时沿桩身缓慢减小。

(3)常规的计算方法高估了基桩的极限扭矩和桩-土体系加载刚度，对于浸水后的膨胀土地基并不适用，实际工程中应考虑地表隆起造成的单桩极限扭矩和桩-土体系加载刚度的降低。

(4)在桩顶扭矩的作用下，浸水前后单桩的桩身扭矩分布规律有着很大的差异，浸水前单桩的桩身扭矩沿桩身近似线性减小，浸水后在“滑移段”桩身扭矩变化较小，“未滑移段”转身扭矩近似线性减小。可根据此特点对膨胀土地区受扭单桩进行合理配筋。

(5)膨胀土的膨胀率会对单桩承载力和桩身扭矩产生较大的影响，随着膨胀率的增加，单桩的抗扭能力明显降低，“滑移段”的长度也在增加。

(6)本文采用有限单元法对膨胀土地基中的受扭单桩进行了分析，由于暂无实测资料，采用室内模型试验进行了验证，并对均质地层中桩身受力情况进行了分析。