低扭转刚度悬索桥扭转发散特征及抗风对策
2020-11-14刘黎阳张志田
刘黎阳,张志田
(1. 云南新创新交通建设股份有限公司,云南 650217;2. 海南大学土木建筑工程学院,海口 570228)
大跨度悬索桥在风荷载作用下容易出现各类气动失稳现象,包括颤振失稳与静风扭转发散[1]。前者为振幅不断增大的气动负阻尼现象,后者为气动负刚度克服结构刚度时表现出的结构变形急剧增大现象[1 − 2]。静风扭转发散具有突发性,对结构的破坏不低于颤振失稳。国内外有较多的文献对大跨悬索桥的静风扭转发散进行了研究,研究对象大多数为公路悬索桥[3 − 6],其失稳形态通常为加劲梁扭转变形的急剧增加。斜拉桥在跨径很大的情况下也存在静风失稳问题[6−7]。桥型基本对称的情况下,加劲梁的扭转变形具有对称性,且变形沿加劲梁的分布没有拐点。这种情况下,迎风侧主缆会得到迅速提升,失稳时其张力会接近空缆悬挂时所对应的状态,从而导致主缆系统提供的扭转刚度基本消失,结构总的扭转刚度出现明显的退化[8 − 12]。与大跨公路悬索桥相比,人马吊桥跨度虽小,但由于主缆间距小且桥面板几乎没有扭转刚度,因而整个系统更容易出现风致扭转发散[13],其发散的形态与公路悬索桥相比是否存在差异缺少充分研究。近年来,旅游业的发展促进了一批人马吊桥的建设,其风致静风稳定性能以及抗风对策值得探讨。
桥梁的抗风性能通常采用风洞试验的方法进行研究,如颤振与涡激共振。但由于突发性与对模型破坏性的特点,参数化的静风稳定性能通常不太适合用试验的方法研究[6, 14]。静风失稳的主流分析理论通常忽略流固耦合效应,因此采用有限元数值方法代替全桥模型试验具有足够的精度[5, 15]。数值方法研究桥梁的静风稳定特性可分为静力有限元法与动力有限元法,前者适合均匀流,后者适合湍流[16 − 17]。从悬索桥刚度退化的机理来看,湍流对扭转发散临界风速能产生重要的影响,但定性分析各种情况的相对优劣,则忽略湍流的静力有限元法完全可满足需求,且有高效省时的优势。
1 低扭刚度悬索桥特征及模型
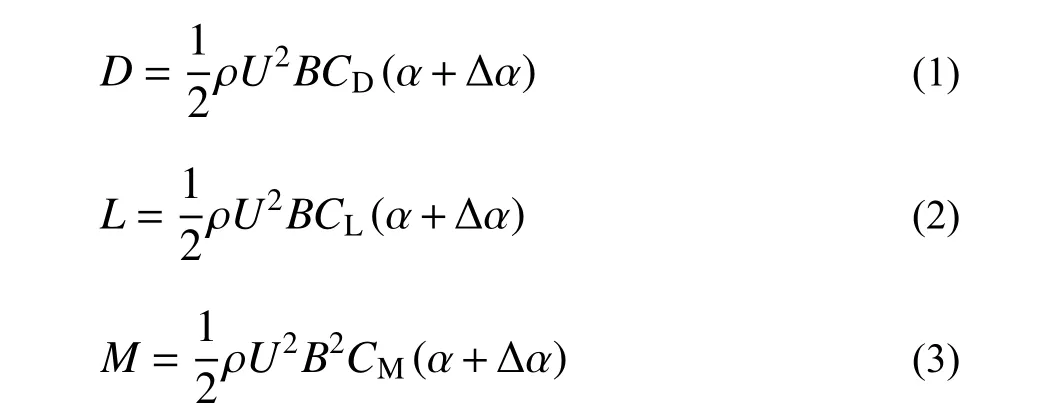
悬索桥传力途径简捷、材料利用效率高且造型优美、规模宏伟,适合建设大跨径桥梁。传统的中小跨径悬索桥根据梁的形式可分为柔性悬索桥和刚性悬索桥,刚性悬索桥又称为加劲梁悬索桥。柔性悬索桥相对刚性悬索桥具有梁刚度小、桥面系构造简单、架设和维护方便、造价低等优点,成为交通不便的山区、旅游景区等跨越沟谷的理想桥型,如云南地区修建了大量跨怒江、澜沧江、金沙江等的柔性悬索桥(又称人马吊桥)。现代大跨度公铁路悬索桥均为加劲梁悬索桥,但加劲梁提供的刚度相对主缆提供的刚度小,因而结构在整体上仍然呈现轻柔以及低自振频率的特征,“刚性”悬索桥的概念也淡化。人马吊桥与现代大跨度悬索桥相比跨度不大,但由于桥面窄,桥面系基本上不提供竖向以及扭转刚度,因而其抗风问题十分突出。
图1 给出了某悬索桥(人马吊桥)的立面设计。该桥主梁174 m,采用双塔单跨布置。主缆矢跨比为1∶10,两主缆间距为5.6 m,吊杆间距为3 m。加劲梁由横梁、小纵梁、桥面钢板、压花钢板三部分组成,桥面板总宽度仅4.5 m,如图2 所示。有限元模型采用单主梁方案。采用欧拉-伯努力空间梁单元模拟加劲梁、横梁以及桥塔;采用单向受拉空间杆单元模拟主缆以及吊杆单元;采用质量元辅助模拟桥面系的平动以及扭转质量。全桥有限元模型共605 个梁杆单元、403 个节点。静风稳定分析时,主缆以及吊杆气动阻力系数按1.0 取值;忽略桥塔所受气动力;加劲梁上考虑阻力、升力以及升力矩,图3 给出了CFD 模拟得到的加劲梁气动阻力、升力以及升力矩系数。每延米加劲梁上所受的气动力按下式进行计算:
式中:D、L、M分别为风轴坐标下单位长度所受的阻力、升力以及升力矩; ρ为空气密度;U为来流风速;B为参考尺度,本文取桥面宽度;CD、CL、CM为阻力、升力以及升力矩系数,它们是来流初始风攻角 α以及加劲梁扭转变形后的附加风攻角 ∆α的函数。有限元求解时,采用内外荷载增量双重迭代的方法搜索结构的平衡位置[5, 15],加劲梁扭转变形 ∆α的收敛精度取0.001°。

图1 某悬索桥立面布置 /mm Fig. 1 Elevation of the suspension bridge concerned

图3 加劲梁静力三分力系数Fig. 3 Aerostatic coefficients of the bridge deck
2 静风稳定特性
图4 与图5 分别给出了0°以及+3°风攻角下结构的变形曲线。每个小图中三条曲线分别代表跨中、左侧四分点、右侧四分点三个位置。两种风攻角下均出现了明显的静风扭转发散临界点,即在某一风速下结构的变形突然出现跳跃式增大。从图中可知0°以及+3°两风攻角下的扭转发散临界风速分别为47 m/s 以及40 m/s。与传统静风扭转发散相比,本桥的静风扭转发散具有如下新的特征:
1)加劲梁反向扭转。已报道的静风扭转发散,加劲梁的扭转变形基本上呈跨中最大、向两侧对称减小的特征。本桥的分析表明,风速达到临界点之前,两四分点的变形是完全对称的(见图6与图7);临界点后,两四分点的扭转以及竖向变形突然出现分岔反向跳跃(见图6)。此外,两边跨向哪个方向扭转具有偶然性,从图4~图6 可知扭转方向呈随机地、交替地变化,但不管是哪种情况,正负两方向的变形分别由各自的变形路径控制。

图4 0°风攻角时变形-风速关系Fig. 4 Deflection-wind speed relation of 0° wind angle of attack
2)加劲梁反向扭转发散后,主缆张力突然增加呈现“锁紧”状态,如图8 所示。临界点之前,随着风速的增加,主缆的张力逐渐下降;但风速增加至临界点后,迎风与背风两侧的主缆张力同时跳跃增加。这一点与传统的静风扭转发散有实质性的不同,后者扭转发散的,迎风侧主缆张力会大幅下降,甚至松弛到空缆悬挂状态。
两种风攻角状态下,最低扭转发散临界风速仅40 m/s,如果考虑湍流的影响,其发散风速会进一步降低。结构扭转发散后,最终的变形决定于结构以及加劲梁气动力的非线性特性。从图3可知升力矩系数随风攻角呈明显的非线性变化特性,其斜率变缓甚至某些区间出现局部负斜率,这些非线性因素会对结构的最终变形起到很强的抑制作用。对本桥而言,扭转发散后结构左右两四分点相对扭转变形比较温和,60 m/s 的风速范围内最大约为30°。

图5 3°风攻角时变形-风速关系Fig. 5 Deflection-wind speed relation of 3° wind angle of attack
3 抗风措施
3.1 增加抗扭刚度

图6 0°风攻角失稳前后加劲梁左右两四分点变形对比Fig. 6 Defection of main girder at two quarter points before and after divergence

图7 3°风攻角时加劲梁变形分布Fig. 7 Deflection along main girder at 3° wind angle of attack
与原桥面系相比,图9 所示的分离双箱断面可明显提升扭转刚度,图中左右两分离箱宽1 m,箱高仅0.3 m,箱室钢板厚10 mm。采用该断面的刚度后重新进行分析可得结构的变形-风速曲线,如图10 所示给出了+3°风攻角下计算结果。为保证可比性,分析中保留原断面的气动力特性,即仍然使用图3 所示的气动力三分力系数。比较图10与图5 可知,提高截面扭转刚度后,静风失稳临界风速从原断面的40 m/s 提高到了70 m/s。此外,扭转发散的特征也有本质性的不同,主要体现在两方面:1)全桥加劲梁不再出现反向扭转现象,从图11 给出的结构变形比较可很清楚地看到这一点;2)扭转发散时,主缆张力不再出现“锁紧”现象,相反,迎风侧主缆逐渐松弛到接近空缆悬挂状态,如图12 给出的缆力分布所示。与图8相比,迎风侧主缆的张力变化明显不同,前者先减小再突然跳跃增大,后者一直减小;前者扭转发散后张力升到1900 kN 以上,后者张力缩减到仅200 kN 左右。
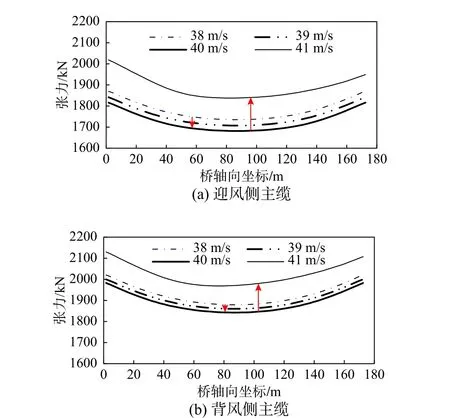
图8 3°风攻角时主缆张力分布Fig. 8 Tension distribution along main cable at 3°wind angle of attack

图9 分离双箱断面 /mmFig. 9 Cross section of a main girder with two separate box-girders
需要指出的是,本桥加劲梁截面扭转刚度提升后,并没有改变其正反对称扭转模态的先后顺序,两种情况均为反对称扭转模态频率低于正对称扭转模态。因此,扭转发散形态的变化与模态顺序没有关系。从本文的分析来看,扭转发散形态更多地决定于加劲梁与主缆系统静力扭转刚度的相对大小,但具体的力学机制仍然有待深入研究。
3.2 反拉抗风缆

图10 双箱断面加劲梁变形-风速曲线:Fig. 10 Deflection of separate box girder via wind speed
反拉抗风缆是大跨度人行桥、人马吊桥或者景观桥一种有效的抗风措施,如图13 所示,在桥面以下设置反向的两根主缆,对桥面系施加与主缆反向的张力以提供额外的刚度,增加其抗风能力。反拉抗风缆的设计涉及多方面参数,主要包括:第一,矢跨比的确定;第二,反拉缆的截面积与主缆截面积的比值;第三,反拉缆的张力大小;第四,反拉主缆所在平面与水平面的夹角如何选取。这些参数不仅决定其抗风效果,也涉及到主缆的材料用量。
3.2.1 反拉张力
图14 给出了仅变化反拉抗风缆张力后的分析结果,每根反拉抗风缆的截面积为0.003705 m2,为单根主缆面积的1/3;反拉抗风缆所在平面与水平面夹角为45°;其垂直向矢高与跨度的比值为1/20;初始风攻角为+3°。

图11 风速70 m/s 时结构变形Fig. 11 Structural global deformation at wind speed 70 m/s
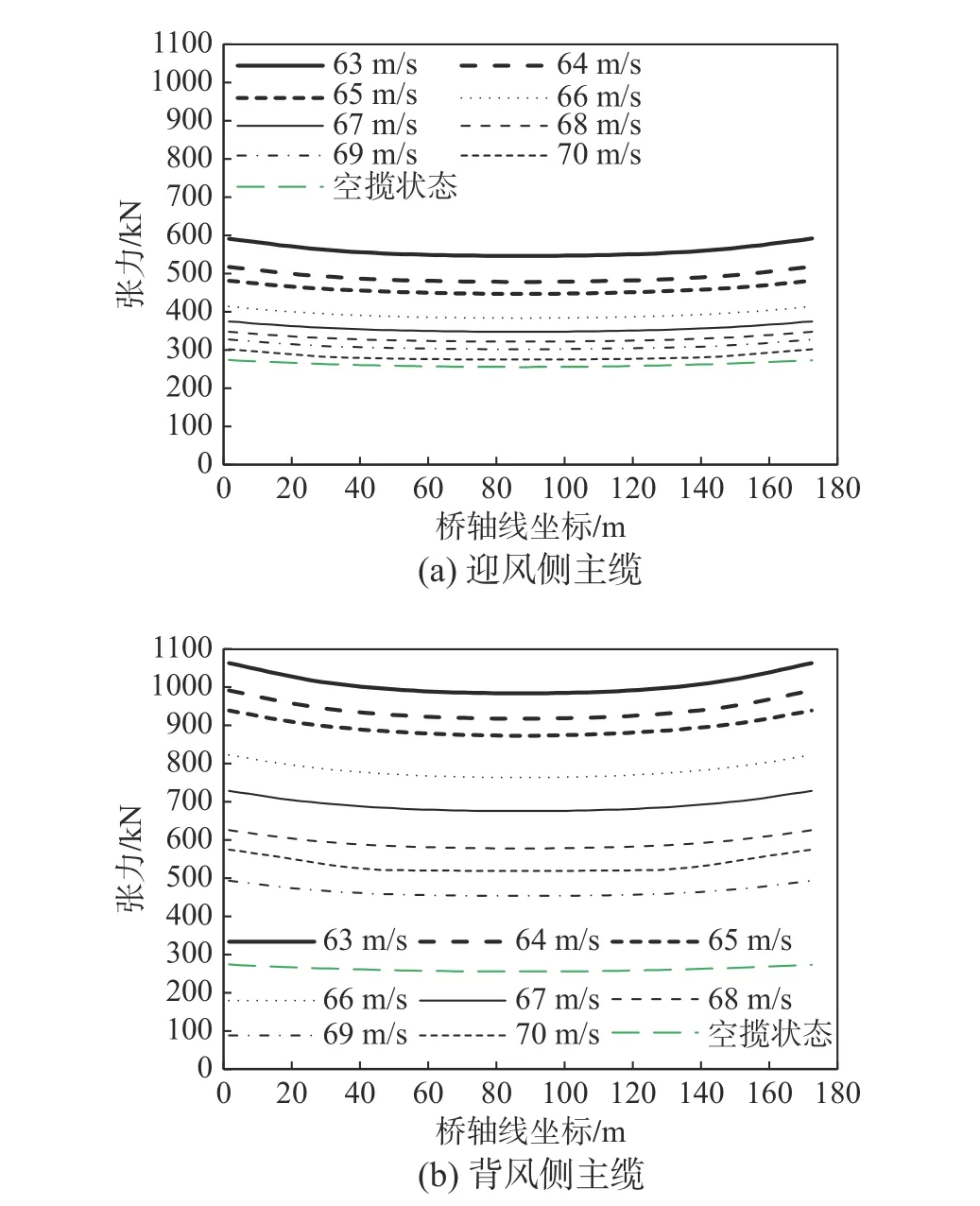
图12 双箱断面桥型主缆张力变化Fig. 12 Tension distributed along main cables of separate box-girder scheme
图13 反拉抗风缆布置方案Fig. 13 Scheme of wind-resistant cables
图14 给出的结果表明,增加反拉抗风缆的张力可以很明显地提高桥梁的抗风稳定性能,主要体现在三方面:其一,反拉张力改变结构的整体变形形态。1/16 与1/8 倍恒载的反拉张力时,跨中为负扭转,两四分点为正扭转,表明扭转变形沿加劲梁方向出现了两个反扭点,整个加载风速范围内两四分点扭转变形无分岔现象。1/2 倍恒载反拉张力时全桥恢复到一个反扭点,两四分点反向扭转分岔“锁紧”主缆,但分岔点出现的临界风速已从原结构的40 m/s 显著提高到73 m/s;其二,与图5(a)原结构的结果相比,反拉抗风缆明显降低了结构变形,如图15 所示。无措施时,风速60 m/s 下最大扭转变形达到23°,增加措施后,四种张力状态下最大扭转变形下降到2°以下。从图15 可知,在所考虑的反拉张力范围内,张力大小并不实质性地影响到最大扭转变形。实际设计时,采用1/4 倍恒载效应产生的反拉张力已经具有很好的效果。

图14 设置反拉抗风缆后变形风速曲线Fig. 14 Deflection-wind speed relation of main girder with wind-resistant cables
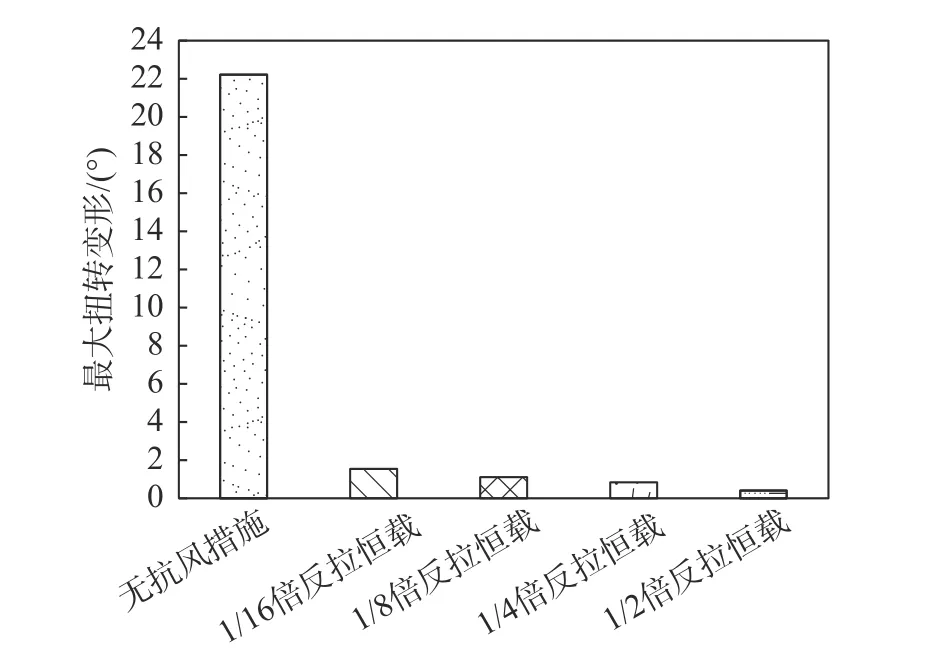
图15 风速60 m/s 下不同反拉恒载方案加劲梁最大扭转变形Fig. 15 Largest deflection along main girder with various wind-resistant cable tensions
3.2.2 反拉风缆面积
图16 给出了反拉抗风缆截面积变化时加劲梁的变形-风速曲线。图中每根反拉抗风缆的反拉张力保持为1/4 倍恒载效应,即反拉主缆面积变大时,应变降低以保持张力不变;反拉抗风缆所在平面与水平面夹角为45°;其垂直向矢高与跨度的比值为1/20;初始风攻角为+3°。
从图中可知,反拉风缆面积增大时,即使结构张力保持不变,整体的扭转响应明显降低。图17给出了无风缆、1/6 倍主缆面积风缆、1/3 倍主缆面积风缆以及1/2 倍主缆面积风缆四种情况的对比。尽管风缆面积越大,结构响应越小,但过大的面积会过于增加结构成本,而降低风致变形的幅度有限。与反拉张力大小的调整类似,四种情况的对比中,从1/6 倍~1/2 倍主缆面积的调整范围内,响应幅值没有本质性变化。
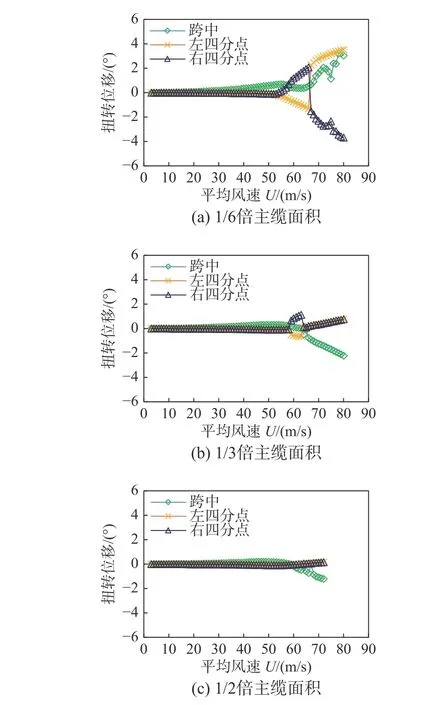
图16 反拉抗风缆面积变化时变形-风速曲线Fig. 16 Deflection-wind speed relation of main girder with various wind-resistant cable areas

图17 风速60 m/s 下不同抗风缆截面积时加劲梁最大扭转变形Fig. 17 Largest deflection along main girder with variouswind-resistant cable areas
反拉抗风缆截面积以及张拉力的选取,须考虑抗风缆本身的安全系数。给定安全系数的情况下,截面积由初始张拉力以及设计风速下结构的整体变形决定。而结构的整体变形受体系刚度以及三分力特性控制。安全系数不变的情况下,张拉力越大则风缆截面积越大;结构整体变形越大则风缆截面积也会越大。
3.2.3 反拉角度
反拉抗风缆的安装角度示意如图18 所示。图19给出了风缆垂直矢高、竖向张力效应、截面积等相同的条件下,六种安装角度下结构响应的对比。从图中可知,15°安装角度下结构响应最小,随着安装角度的增加,结构的响应逐渐增大,当安装角度达到90°即抗风缆与主缆在同一垂直平面内时结构响应最大。需要指出的是,图19 中给出的六种情况均保持了相同的竖向张力效应,这意味着安装角度越小,抗风缆中的张力越大,因此尽管小角度时对静风稳定性的增加效果大,但抗风缆本身的安全系数却会降低。实际工程中,建议最佳安装角度选取15°~45°。
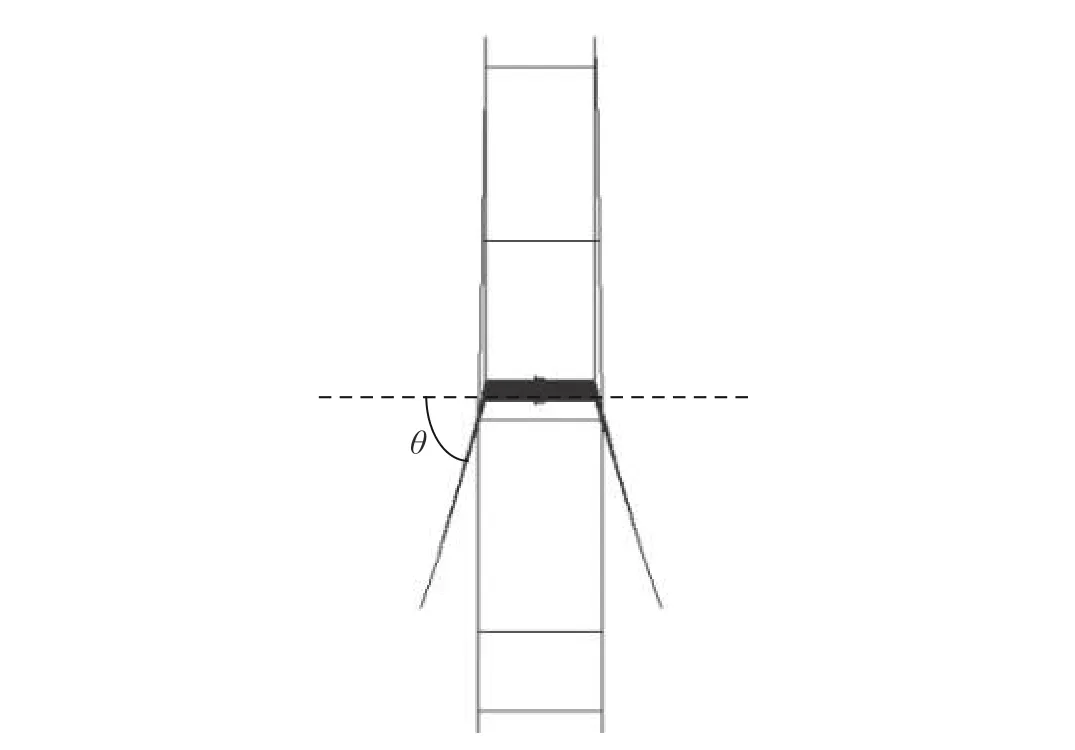
图18 风缆安装角度Fig. 18 Installation angle of wind-resistant cables
3.2.4 反拉缆矢跨比
对抗风缆矢跨比进行调整,选取1/10 以及1/20两种情况进行了对比,如图20 所示。安装角度均为90°、每根反拉抗风缆的截面积均保持为1/3 倍主缆面积、反拉张力均为0.25 倍恒载效应。
图19(f)以及图21 分别为反拉风缆矢跨比为1/20 以及1/10 时结构响应的对比。从两图的对比可知,调大矢高后,结构响应产生两方面的变化。首先最大响应明显降低,其次是反向跳跃扭转发散的临界风速明显提高,因此,增加抗风缆的矢高可提高其抗风能力。

图19 反拉抗风缆不同安装角度对比Fig. 19 Comparison among installation angles of wind-resistant cables

图20 抗风缆不同垂直矢高方案有限元模型对比Fig. 20 FEM models with different sag ratios of wind-resistant cables

图21 抗风缆1/10 矢跨比时结构响应Fig. 21 Deflection of main girder with windresistant cables of 1∶10 sag ratio
4 结论
本文对低扭转刚度人马吊桥的静风扭转发散特点以及相应的抗风措施进行了详细的分析,综合以上的分析结果可得以下研究结论:
(1)低扭刚度人马吊桥静风扭转发散时,加劲梁会出现单拐点或多拐点反向分岔扭转锁定现象。该类扭转发散与常规箱形或桁架悬索桥的静风扭转发散有着本质性的不同,前者扭转发散时主缆张力突然增加,加劲梁扭转变形有拐点;后者扭转发散时主缆张力迅速降低至空缆悬挂状态,加劲梁扭转变形无拐点。
(2)改变加劲梁的断面形式,适当增加其扭转刚度能显著提高静风扭转发散临界风速,且能改变扭转发散的类型,从有拐点扭转发散转变为无拐点扭转发散。
(3)反拉抗风缆的设置可明显提高静风稳定性,其抗风效果随张拉力、抗风缆面积、垂直矢高的增加而增加。建议抗风缆的反拉张力取1/4 倍恒载效应,面积取主缆的1/3,地形允许的情况下尽量增大其垂直矢高。抗风缆最佳安装角度可在15°~45°选取,地形允许的情况下尽量选择偏小的角度。
