自复位超弹性SMA 筋梁柱节点数值模拟研究
2020-11-14李宗翱裴金召康莉萍
钱 辉,李宗翱,裴金召,康莉萍
(1. 郑州大学土木工程学院,河南,郑州 450001;2. 成都基准方中建筑设计有限公司郑州分公司,河南,郑州 450006)
梁柱节点作为框架结构的主要组成部分,承担着分配弯矩、传递剪力和轴力的作用。大量震害调查表明,框架节点在地震作用力下易于受损,节点的破坏失效会引发整体结构的破坏甚至倒塌[1]。因此,提高框架节点的抗震性能对提高整个框架结构的抗震性能尤为重要。
传统的抗震设计方法会导致构件或结构在强震后产生严重的损伤及较大的残余变形,最终导致结构难以修复而不能继续使用。近年来,具有自复位、高耗能等特点的可恢复功能防震结构已经成为国际地震工程界的研究热点[2 − 3]。
形 状 记 忆 合 金(shape memory alloy,SMA)具有超弹性、高阻尼、耐疲劳及耐腐蚀等特性,能显著提高结构的耗能能力和损伤自修复能力,减小结构震后的残余变形。因此其在可恢复功能防震结构体系中具有较好的应用前景[4 − 8]。
近年来,国内外学者对基于SMA 的自复位结构体系进行了大量研究,取得了一系列成果。Qiu和Zhu[9]对一种新型SMA 支撑自复位钢框架进行了试验研究和数值计算。结果表明:SMA 支撑作为一种独立的抗震构件在中强地震条件下具有良好的抗震性能,能够承受多次强震,且功能不退化。大震下,钢框架损伤较小而且残余变形为零。程光明[10]提出了两种基于SMA 的自复位钢连梁体系,并采用ANSYS 有限元软件进行了数值模拟。结果表明:该自复位连梁体系,在循环荷载作用下,仅SMA 棒出现屈服,其余构件都处于弹性范围内。超弹性SMA 棒可以使钢连梁恢复到初始位置,有良好的自复位能力,而且能够提供一定的耗能能力。刘文渊等[11]等提出了一种新型自复位SMA 耗能梁段,将Y 型偏心支撑中耗能梁段的腹板更换为SMA 材料。使用ANSYS 有限元软件建立模型分析。结果表明:与传统耗能梁段相比,SMA 耗能梁段具有旗帜形滞回曲线,承载力及延性无明显下降,可实现震后结构自复位。李灿军等[12]在梁柱节点中引入NAO(非石棉)摩擦耗能器和超弹性形状记忆合金(SMA)杆,形成摩擦耗能型SMA 杆自复位梁柱节点(NAO-SMA-SC),基于OpenSess 进行了数值模拟和参数分析。结果表明:在节点中引入摩擦耗能器,能明显地提高节点抗弯能力和耗能能力,但同时会增大节点残余变形;随着SMA 杆直径的增大,节点抗弯能力和自复位性能均显著提高;SMA 杆预应变的施加能有效降低节点的残余变形。Mahmoud 等[13]将桥梁柱塑性铰区普通钢筋和混凝土替换为SMA和ECC,以减小柱在强震作用下的永久变形和损伤。试验和OpenSees 数值模拟结果表明:超弹性SMA 材料能提高结构的变形能力,ECC 可以减少结构的损伤,在三组构建中,SMA/ECC 桥梁柱性能变形能力最好,损伤最小。王伟等[14]在钢节点梁端连接处使用了SMA 腱和角钢来提高钢节点的自复位和耗能能力。试验和数值模拟结果均表明:角钢的厚度和SMA 腱的预应力大小对于节点的初始刚度、自复位能力、耗能能力有较大的影响。较薄的角钢和较高的SMA 腱预应力虽然使初始应力和耗能能力较低,但保证了节点的自复位能力。
目前采用有限元模拟节点的方法主要有以下3 种:1)在梁柱单元端部添加塑性铰;2)将节点简化为零长度转动弹簧单元;3)在梁柱端添加剪切元件和钢筋粘结滑移弹簧。相较于第一种,第二种方法能够比较简单地反映剪切响应,但是前两种方法均不能考虑钢筋与混凝土的粘结锚固性能。第三种方法可以较好地模拟节点剪切失效和钢筋混凝土粘结滑移失效[15 − 17]。
为了提高框架结构的耗能能力和自恢复能力,提出了基于超弹性SMA 筋的功能自恢复梁柱节点。本文基于OpenSees 有限元软件平台,采用SMA 材料自复位双旗形本构模型,建立了自复位SMA 筋混凝土梁柱节点有限元数值模型,进行了低周往复作用下有限元模拟,得出了节点的滞回曲线与骨架曲线。通过与现有的试验结果的对比,验证了节点分析模型的有效性。进行了参数分析,分别考虑了SMA 材料的配置数量、配置长度和屈服强度等参数,分析了SMA 材料参数对节点的滞回性能和自复位能力等性能的影响。
1 试验概况
1.1 试验模型
本文有限元数值模拟在完成的模型试验数据基础上进行,模型试验详细过程及结果分析见文献[18],这里仅作简要介绍。试验选取6 层钢筋混凝土框架结构在侧向荷载作用下相邻梁柱反弯点之间边节点单元作为研究对象。该框架结构标准层高3.3 m,纵向跨度6 m,柱截面尺寸600 mm×600 mm,梁截面尺寸300 mm×600 mm。依据相似理论,制作了2 个1/2 缩尺节点试验模型,即普通钢筋混凝土节点(JD-RC)和超弹性SMA 筋节点(JD-SMA)。试件的尺寸和配筋如图1 所示。
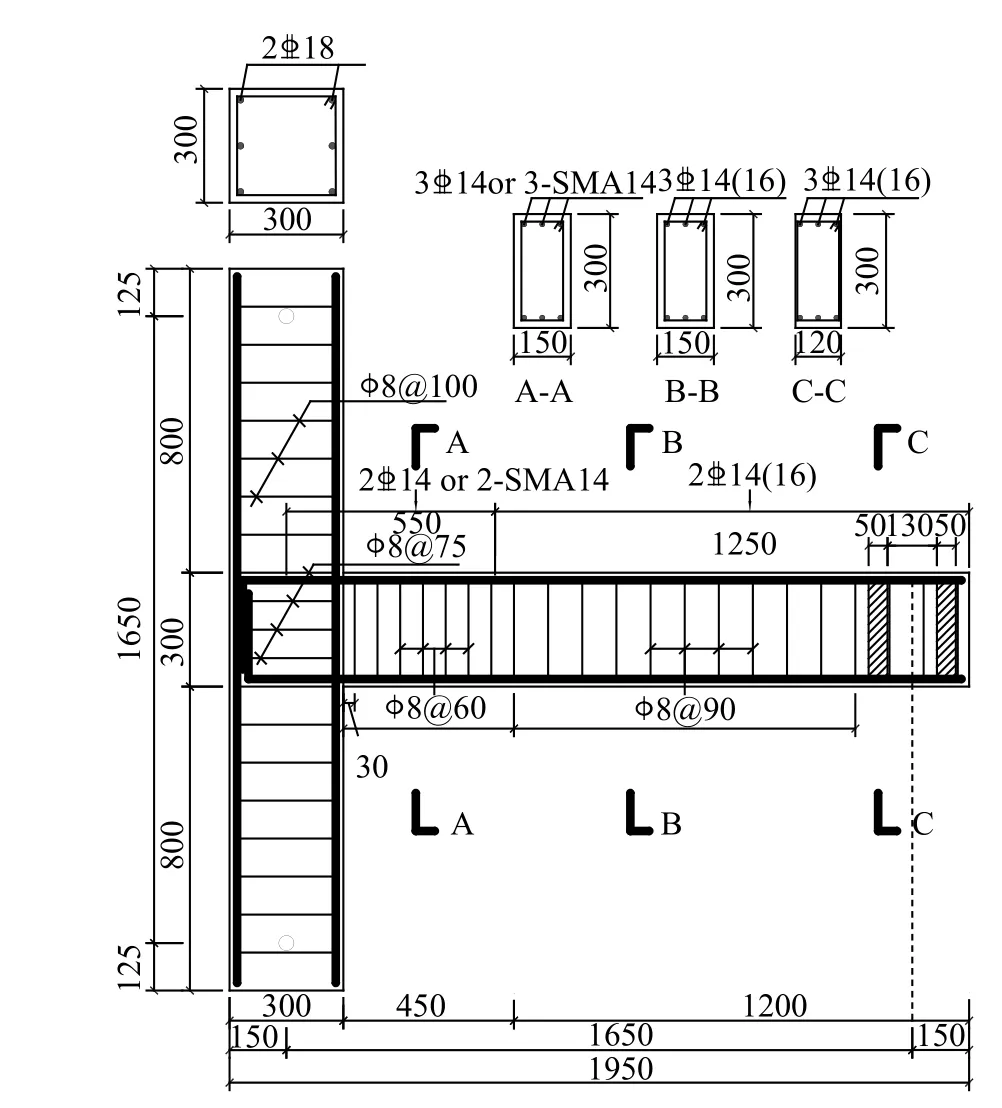
图1 试件配筋详图Fig. 1 The details of the joints
在梁端塑性铰区(1 倍梁截面高度)用SMA 筋代替普通纵向受力钢筋,为了避免连接件破坏,将连接部位向节点核心区移动150 mm,如图2 所示。SMA 筋与钢筋采用套筒连接,如图3 所示。
1.2 试验材料
试验采用的SMA 材料是西安思维金属有限公司生产的SMA 棒材,直径为14 mm,主要材料成分占比为55.86%Ni 和44.14%Ti。奥氏体相变结束温度Af为5 ℃。
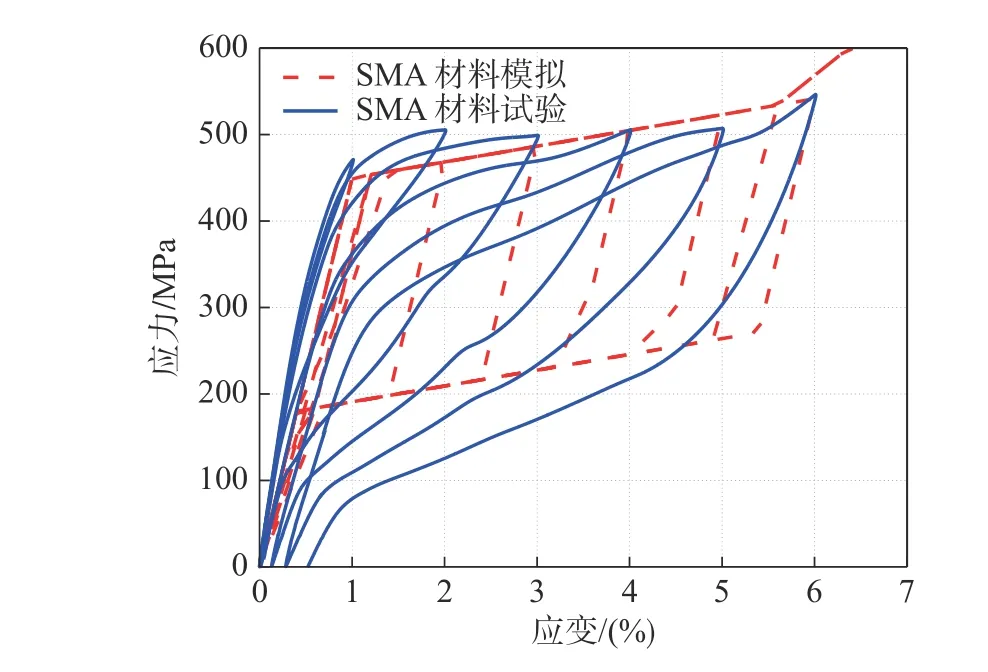
首先对SMA 进行热处理,将加工好的SMA试件放入400 ℃的高温炉中保温15min,之后取出水冷。然后再进行拉伸试验。材料试验结果表明,SMA 的弹性模量为66.3 GPa,屈服强度为450 MPa 左右。应变幅值达到6%时,最大残余应变为0.52%,可恢复变形为86.7%,如图4 所示。

图2 JD-SMA 节点详图Fig. 2 The detail of the JD-SMA joint

图3 SMA 筋和钢筋连接示意图Fig. 3 The link of SMA bars and rebar

图4 Ni-Ti SMA 筋应力-应变关系曲线Fig. 4 Stress-strain curves of Ni-Ti SMA bar
该构件中纵向钢筋为HRB400 级,箍筋为HPB 300 级,不同直径的钢筋力学性能详见表1。混凝土强度等级为C30,根据材性试验结果,混凝土标准立方体试块抗压强度取44.8 MPa。

表1 钢筋力学性能指标Table 1 The parameters of steel bars
1.3 加载方式
试验采用梁端加载方式。将上柱端简化为滑动支座,下柱端简化为固定铰支座,梁端为自由端。在上柱端施加恒定轴力664 kN,在梁端施加往复荷载,如图5 所示。

图5 加载装置Fig. 5 Test setup
本试验加载制度为荷载-位移混合控制加载,试件屈服前,采用荷载控制并分级加载,每级循环一次。试件屈服之后,采用位移控制,以屈服位移Δ的整数倍为级差分级加载,每级循环2 次。当荷载降低至峰值荷载的80%时停止加载。如图6 所示。

图6 加载制度Fig. 6 Loading protocol
2 有限元模型的建立
2.1 材料本构模型
2.1.1 SMA 材料本构模型
SMA 材料选用OpenSees 中的自复位本构模型[19],如图7 所示。应力-应变曲线变化规则为以下四点:
1)弹性阶段,在应力小于fy时,加载、卸载均沿着以k1(第一刚度)为斜率的直线。
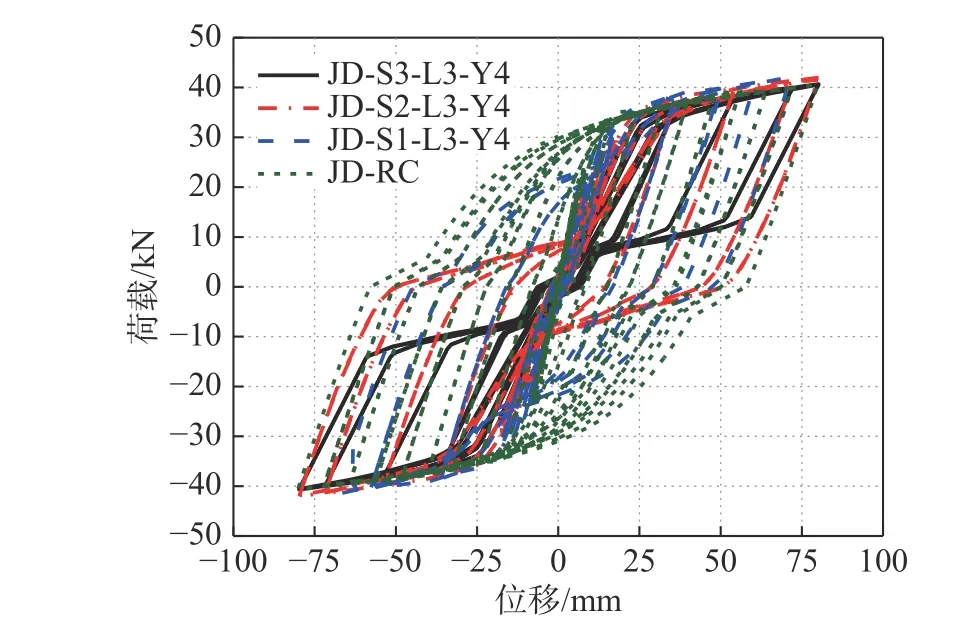
2)应力大于fy后,加载过程沿着以k2(0 3)硬化阶段,应变大于εb。在εb<ε<εu时,加载卸载均沿斜率为r·k1(r为硬化刚度系数,0 4) SMA 受压行为虽与受拉有所差别,但是影响较小,所以受压部分与受拉部分对称建模。 图7 SMA 本构模型Fig. 7 Constitutive model of SMA 该本构模型采用7 个参数来定义,参数取值列于表2。根据材料试验模拟了SMA 拉伸试验,对比验证了SMA 自复位模型,如图8 所示。 表2 SMA 自复位模型参数及取值Table 2 The parameters and values of selfcentering 2.1.2 钢筋理论模型 钢筋采用基于Chang 和Mander 单轴钢筋模型本构模型[20],该模型能较好地模拟钢筋因疲劳与屈服引起的刚度退化,如图9 所示。该本构模型分为3 个阶段:弹性阶段、屈服阶段、硬化阶段。应力-应变关系表达式如式(1)~式(6)所示。 图8 SMA 棒材单轴循环拉伸应力-应变曲线模拟Fig. 8 Numerical simulation of SMA stress-strain curve under cyclic tension load 图9 Menegotto 和Pinto 钢筋本构Fig. 9 Menegotto and Pinto constitutive model of steel bar 2.1.3 混凝土理论模型 混凝土模型采用修正Kent-Park 混凝土本构模型[21],如图10 所示。在Kent-Park 模型的基础上,考虑了箍筋的约束效应。该本构模型分为三个部分:上升段、下降段、平台段。约束混凝土应力-应变关系表达式如式(7)~式(13)所示。 图10 修正Kent-Park 混凝土本构Fig. 10 Modified Kent-Park model for concrete 式中:ε0为混凝土峰值压应力对应的应变;ε20为峰值应力下降到20%时的应变;K为箍筋约束强化系数;fc′为混凝土圆柱体抗压强度;fyh为箍筋屈服强度;ρs为体积配箍筋率;h″为核心混凝土宽度;Sh为箍筋间距;εcu为混凝土极限压应变。 在OpenSees 中,由Lowes 等提出并由Mitra改进的节点宏观力学模型,能够较好地表现梁柱节点在低周反复荷载作用下的受力特性[22]。该节点模型针对节点处的三种主要受力破坏失效形式,采用了3 种元件来模拟:剪切板元件用来模拟核心区的剪切失效;零长度钢筋粘结滑移弹簧来模拟钢筋与混凝土的粘结滑移失效;零长度交界面剪切弹簧来模拟节点四周剪切破坏失效,如图11 所示。 图11 节点宏观力学模型Fig. 11 Macroscopic mechanical model of joints 剪切板元件采用“Pinching4”模型建立。该一维荷载-变形滞回模型,基于MCFT 修正斜压场理论[21]计算节点核心区剪应力-应变关系,得出剪切板的参数,如图12 所示。钢筋粘结滑移模型为基于此模型的“Bar-silp”材料,根据节点区钢筋混凝土的参数,得出滑移弹簧的模型。交界面剪切弹簧定义为一个弹性模量极大的弹性弹簧,这是由于该现浇节点的交界面处抗剪刚度较大,均在弹性范围之内。 图12 一维荷载-变形滞回模型Fig. 12 One-dimensional load-deformation hysteretic model 根据材料力学性能试验结果,得出参数继而确定有限元模型中各个材料与元件的参数。按照各构件在试验过程中每个循环的实际位移,采用位移控制加载。对比分析模拟数据与试验数据,从滞回曲线、骨架曲线、刚度退化、残余位移、耗能能力5 个方面,验证模型的正确性和适用性。 图13 给出了自复位SMA 梁柱节点和普通混凝土节点梁端荷载-位移滞回曲线的数值模拟结果与模型试验结果对比情况。图13(b)中,模型较好地模拟了SMA 节点呈现的“双旗形”自复位特性。最后两级位移加载曲线出现了区别,这是由于试验过程中钢筋-SMA 连接处断裂而导致的。由图13 可以看出,节点数值模拟滞回曲线与试验结果一致,较好地体现出了模型的适用性。 图13 节点梁端荷载-位移滞回曲线对比Fig. 13 Comparison of load-deformation hysteretic loops at beam ends 根据数值模拟结果,滞回曲线的外包络图得到2 组构件的骨架曲线,如图14(a)所示。采用环线刚度来评价构件的刚度退化,如图14(b)所示。由节点屈服后每个滞回阶段结束后产生的残余变形,评价其自复位能力,如图14(c)所示。由试件每级加载滞回环的面积得出能量耗散曲线,如图14(d)所示。 图14 数值模拟性能曲线和试验性能曲线对比Fig. 14 Comparison of the behavior curves between numerical data and test results 从图14 可明显看出,由数值模拟数据得到的骨架曲线、刚度退化曲线、残余变形和耗散能量与模型试验结果基本吻合,表明本文建立的有限元数值模拟模型可以较好地模拟节点在低周往复荷载作用下的各项力学性能,能够准确地反映构件的抗震性能,验证了模型的正确性和适用性。 为了对框架节点进行优化设计,基于已建立的数值模拟模型,对节点抗震性能进行了参数优化分析。分别考虑了SMA 的配置数量、替换长度及屈服强度等设计参数,通过有限元模拟分析了不同参数对SMA 梁柱节点滞回性能、自复位能力及耗能能力等性能的影响,探讨了各参数的影响规律。 表3 给出了框架节点参数分析方案。基于现行混凝土结构设计规范[23],在梁端截面适筋条件下,考虑3 种SMA 配置数量,即:替换2 根、4 根或6 根。考虑了4 种替换长度,即:从柱边起175 mm、225 mm、300 mm 或375 mm。此外,为了研究SMA屈服强度对节点性能的影响,考虑了3 种屈服强度,分别为:335 MPa、400 MPa 或500 MPa。 表3 SMA 框架节点参数分析方案Table 3 Parameters of SMA frame joints 考虑三种SMA 配置数量,即替换2 根、4 根或6 根。图15 给出了梁截面SMA 配置示意图,截面位置见图1 中A-A 截面。图16、图17 为该组试件的数值模拟和分析结果。 从图17 可以看出:适筋情况下,总配筋量相同时,随着SMA 替换数量的增加,会使得SMA混凝土节点承载力稍有降低,初始刚度和耗散能量有所降低。这是由于SMA 筋的弹性模量相比钢筋较低,多次循环后屈服强度低于钢筋的屈服强度造成的。然而,SMA 混凝土节点呈现更加明显的“双旗形”滞回曲线,刚度退化速度减缓,节点残余变形明显减小,自复位能力显著增强。这是由于SMA 筋越多,提供的回复力越来越大,且屈服后SMA 弹性变形能力较大 图15 SMA 替换数量Fig. 15 The number of SMA bars instead of steel bars 图16 不同配置数量滞回曲线Fig. 16 Load-displacement hysteretic loops with different SMA amounts 图17 不同配置数量节点性能曲线比较Fig. 17 Comparisons of the behavior curves between different SMA amounts 为研究SMA 棒材替换长度的影响,考虑了四种替换长度,即从柱边起175 mm、225 mm、300 mm或375 mm(梁端塑性铰区长度为300 mm)。图18、图19 为该组试件的模拟和分析结果。 由图18~图19 可以看出:SMA 替换长度小于塑性铰区长度时,替换长度变小,承载力小幅增加,初始刚度增大,残余变形增大,自复位能力降低,耗能能力稍有增加。SMA 替换长度大于塑性铰区长度时,各项数据对比差别较小,自复位能力提高不明显。因此,可以得出:在梁端塑性铰区长度使用SMA 替换纵筋,综合效果最佳。 SMA 材料发生正相变时的强度被称为SMA的屈服强度,和不同等级的钢筋一样,不同强度等级的SMA 也会对试件的滞回性能产生影响。为了保证梁端SMA 首先屈服形成塑性铰,所以SMA的屈服强度不宜过大。因此,在保证自复位机制的前提下,设计了3 个不同SMA 屈服强度的节点试件,其SMA 屈服强度分别为335 MPa、400 MPa和500 MPa。图20、图21 分别为这组试件的数值模拟和分析结果。 图18 不同替换长度滞回曲线Fig. 18 Load-hysteretic loops of different SMA length 图19 不同替换长度节点性能曲线比较Fig. 19 Comparison of the behavior curves between different SMA length 图20 不同屈服强度滞回曲线Fig. 20 Load-hysteretic loops of different SMA yield strength 由图20、图21 可以看出:随着SMA 屈服强度地增加,承载力大幅提高,初始明显增大,初始刚度增加,刚度退化幅度均一致,残余变形略有减小,自复位能力有一定提升,耗能能力逐渐提高。由此,可以得出:在保证梁端SMA 先屈服的条件下,提高SMA 的屈服强度可以提高节点的抗震性能。 图21 不同屈服强度节点性能曲线比较Fig. 21 Comparison of the behavior curves between of different SMA yield strength 本文基于OpenSees 有限元软件平台,建立了自复位SMA 筋混凝土梁柱节点有限元数值模型,进行了低周往复荷载作用下有限元模拟,模拟结果与试验结果进行了对比。考虑了SMA 材料的配置数量、配置长度和屈服强度等参数,分析了SMA 材料参数对节点的滞回性能和自复位能力等性能的影响。通过分析研究,本文得出以下几点结论: (1)提出的自复位超弹性SMA 筋钢筋混凝土节点具有显著地自复位能力,较好的滞回特性,能够实现结构的功能可恢复。 (2)建立的SMA 节点模型可以较好地模拟SMA梁柱节点在低周反复荷载作用力下的力学性能。 (3)适筋条件下,SMA 配置数量越大,残余位移越小,复位能力越强。 (4)相同条件下,SMA 筋的替换长度小于梁端塑性铰长度时,自复位能力明显降低;当长度超过塑性铰长度后,对节点性能影响不大。 (5)适筋条件下,提高SMA 筋的屈服强度会提高节点的承载能力以及自复位能力。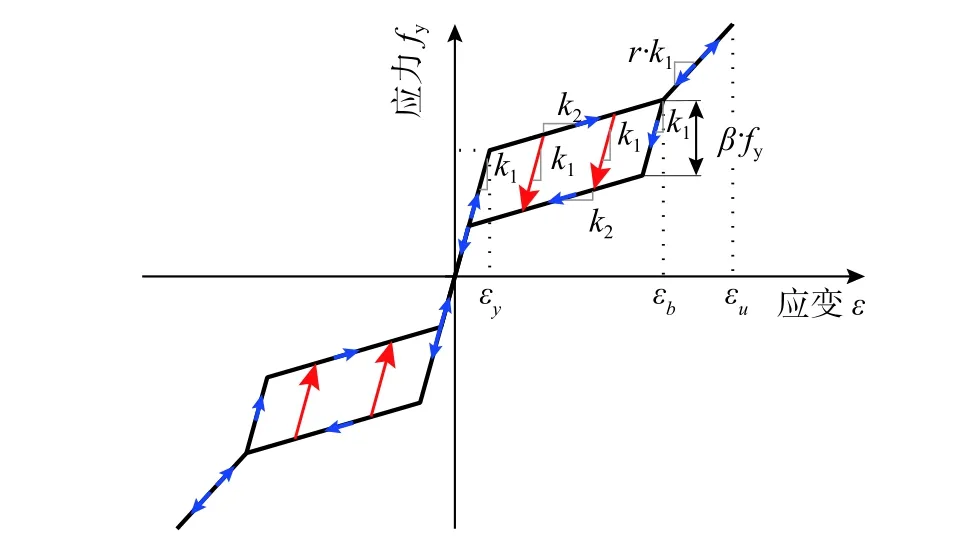





2.2 节点单元模型


3 数值模拟及模型验证
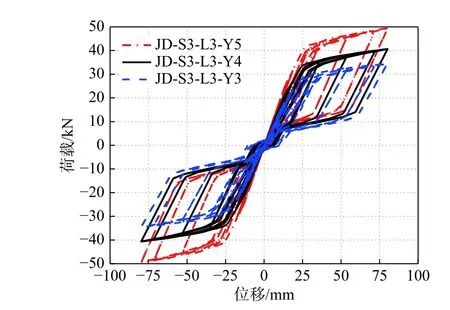
3.1 滞回曲线

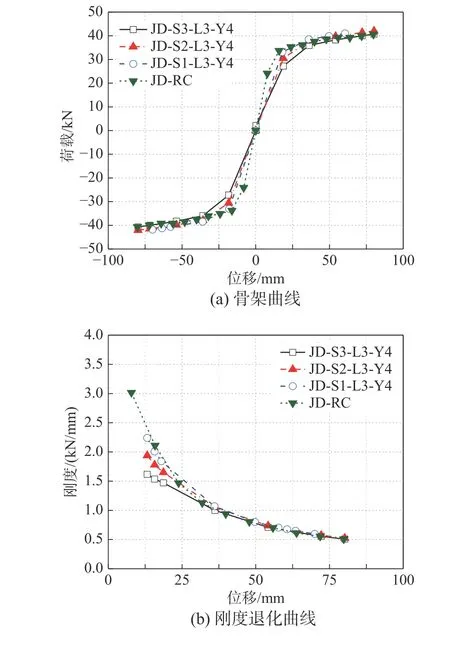
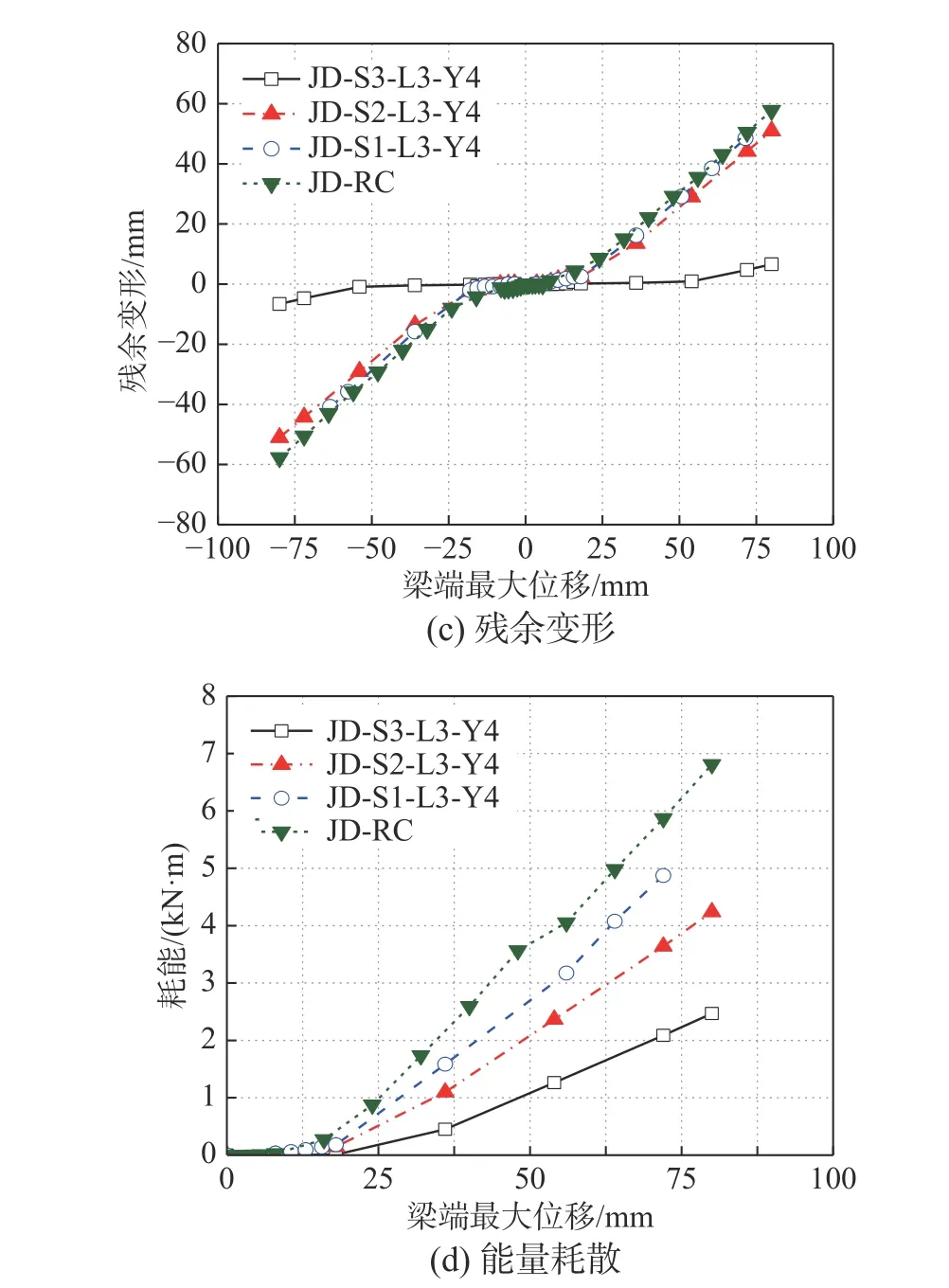
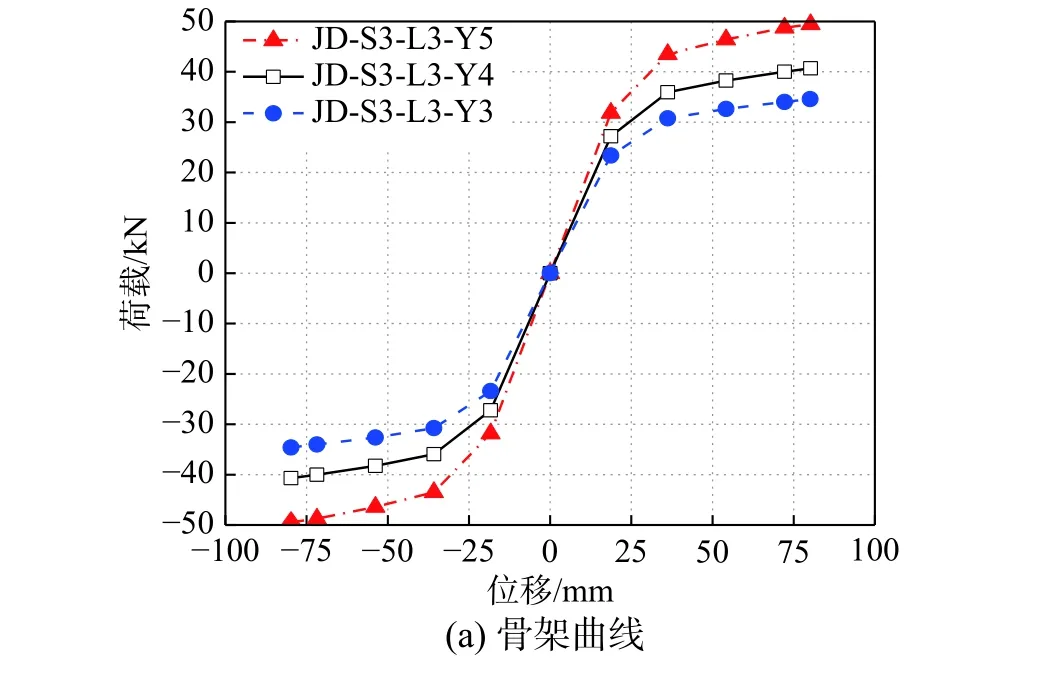
3.2 数据分析

4 参数分析

4.1 SMA 配置数量的影响

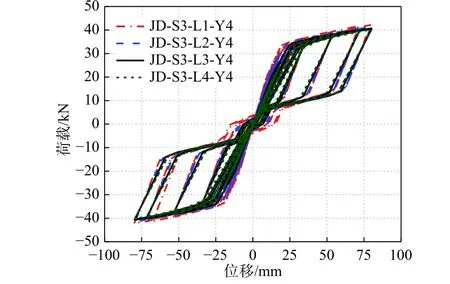
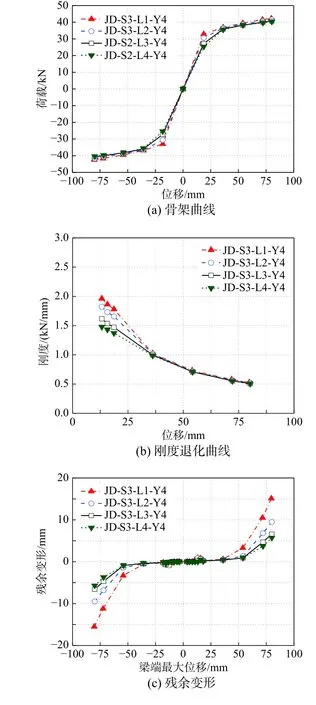
4.2 SMA 替换长度的影响
4.3 SMA 屈服强度的影响


5 结论
