适用于黏土的分数阶应力诱导剪胀方程
2020-11-14李海潮盛岱超
李海潮,马 博,张 升,2,盛岱超
(1. 中南大学土木工程学院,湖南,长沙 410075;2. 高速铁路建造技术国家工程实验室,湖南,长沙 410075;3. 悉尼科技大学土木与环境工程学院,澳大利亚,悉尼 NSW 2007)
不同于正常固结重塑土,超固结重塑土应力-应变曲线具有应变硬化和软化特征,并且伴随着剪缩和剪胀现象的发生。修正剑桥(modified Camclay, MCC)模型[1]在描述其力学特性时存在明显不足,具体表现在以下几个方面:
首先,MCC 模型的剪胀方程假定土体的剪胀因子仅与当前剪切应力比有关,无法考虑温度和超固结比等外部加载因素对土体剪胀特性的影响[2 − 5]。Gao 等[6]在其所建立边界面模型中深入的探究了黏土的应力历史对其剪胀特性和应力-应变特性的影响。值得注意的是,即使对于正常固结重塑土,MCC 模型的剪胀方程在描述其剪胀特性时依然存在不足。Wang 和Yin[7]针对自然软土的试验结果表明,在材料发生剪缩破坏的过程中,MCC 模型预测的剪缩量要明显小于试验值。杜修力等[8]基于统一非线性强度理论建立了适用于正常固结重塑土的剪胀方程。殷杰[9]通过引入结构屈服应力参数建立了适用于结构性软黏土的修正剑桥模型。
其次,MCC 模型采用相关联的流动法则,并且基于非线性能量耗散方程假定土体具有椭圆形屈服面。然而试验结果表明,岩土材料的屈服面具有更为复杂的几何形状[2, 10]。Lagioia 等[11]讨论了屈服面几何形状对模型计算结果的影响;Collins和Kelly[12]则基于现代热力学理论给出了适用于岩土材料的双参数屈服函数。此外,剪切过程中岩土材料塑性流动方向并不始终垂直于其物理屈服面[13 − 14]。Sun 等[15 − 18]指出可以对屈服函数进行分数阶微分得到分数阶塑性流动法则,进而在不引入塑性势函数的情况下统一的描述相关联和非相关联的塑性流动法则。在此基础上,孙逸飞和沈杨[19]建立了适用于粗粒料的静动力边界面模型,成功地模拟了粗粒料在静动力加载条件下的应力-应变行为和循环荷载下的长期变形。Lu 等[20]则基于该方法在 β应力空间建立了适用于正常固结重塑土的分数阶修正剑桥模型。
MCC 模型在描述黏土在超固结状态时的应力-应变响应时同样存在明显不足,模型计算得到的剪切强度明显偏大,且应力-应变曲线为一条不光滑的曲线[21]。为了克服该不足,Dafalias 等[22 − 23]和Hashiguchi 等[24 − 26]分别提出了边界面和下加载面的力学概念。其中,下加载面模型假定在任意加载时刻,材料当前的应力点始终位于下加载面上并发生弹塑性体积变形[27−31];边界面模型则假定当前应力点位于边界面内,并且采用某种映射准则计算得到其塑性流动方向和塑性模量[32 − 36]。
本文首先将Caputo 微分方法应用于MCC 模型的屈服函数,从而得到一个新的分数阶剪胀方程用于考虑超固结比对黏土剪胀特性的影响。在此基础上可以建立适用于黏土的分数阶下加载面模型,该模型所采用的分数阶塑性流动法则能够统一的描述相关联和非相关联的流动法则。相比较MCC 模型,本文模型仅额外地引入了一个与土体剪胀特性相关的模型参数,同时能够对超固结黏土的应变软化和剪胀特性进行合理的描述。
1 应力诱导分数阶剪胀方程

1.1 分数阶微分定义

孙逸飞和沈杨[19]指出分数阶微分具有长程记忆性,适用于描述路径和记忆依赖性行为。后文将根据分数阶微分推导出一个新的应力诱导剪胀方程,并由此建立一个适用于超固结重塑土的分数阶下加载面模型。
1.2 分数阶塑性流动法则


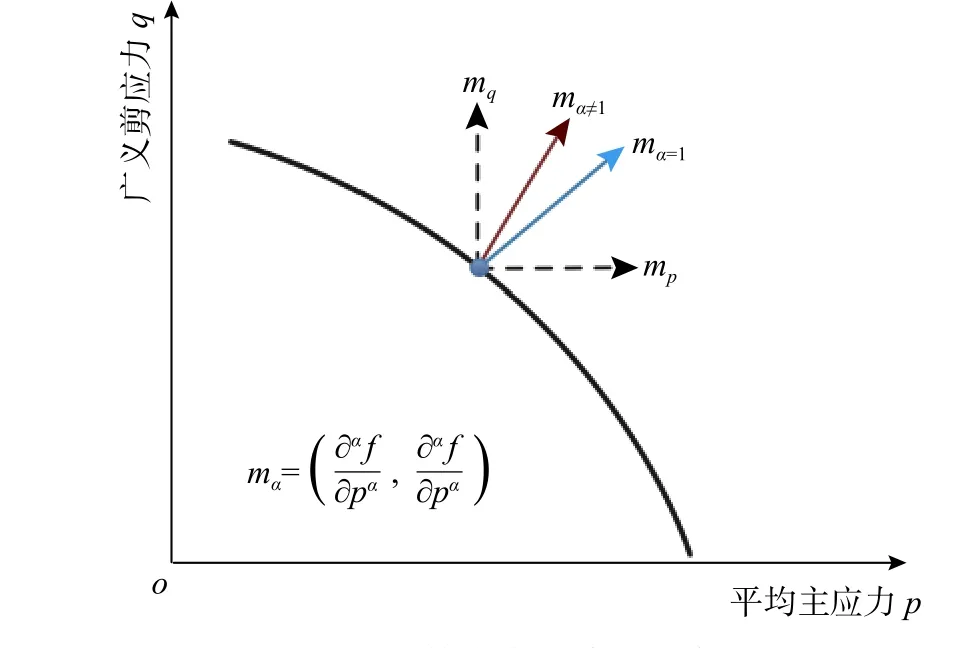
图1 分数阶流动法则示意图Fig. 1 Schematic plot of fractional flow rule
1.3 正常固结屈服面和相似因子
为了表述超固结重塑土的应变软化和剪胀特性,本文引入了下加载面的力学概念。如图2 所示,表征超固结状态的当前应力点A(p,q)位于下加载面上,而参考应力点B(p¯,q¯)则位于正常固结屈服面上。为了动态地描述在p−q平面中下加载面和正常固结屈服面两者之间相对位置的演变关系,基于径向映射法则定义了相似因子R:
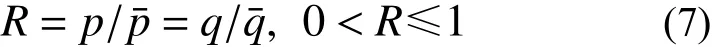
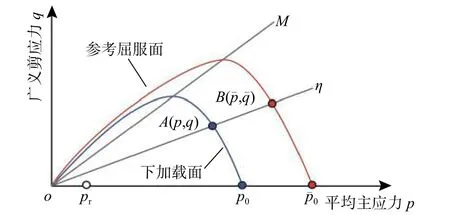
图2 下加载面示意图Fig. 2 Schematic plot of sub-loading surface
R与超固结比OCR具有相似的物理意义,在单调加载过程中,随着土体超固结特性的减弱,R的值逐渐增大,当R=1 时,下加载面与正常固结屈服面最终重合,此时土体处于正常固结状态。

1.4 分数阶剪胀方程

MCC 剪胀方程无法反映温度和超固结性等外部加载因素对土体剪胀特性的影响,同时对于超固结重塑土,该剪胀方程预测的剪胀量要明显大于实测值。为此,联合式(5)、式(9),本文基于Caputo 分数阶微分给出了一个新的剪胀方程:


图3 给出了剪胀因子d随剪应力比 η和相似因子R的变化规律。可以看出,在相同的应力水平下,d随着R的增大而逐渐增大,即黏土的剪胀量会随着超固结性的破坏而逐渐增大,与试验结果保持一致。
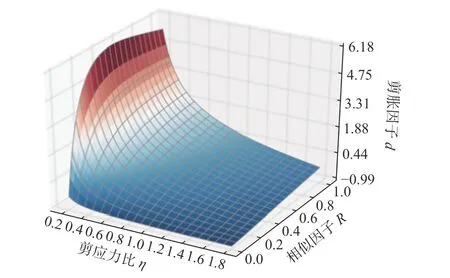
图3 剪胀因子d 随剪应力比 η和相似因子R 变化规律Fig. 3 Evolution of dilatancy ratio d with shear stress ratio η and similarity ratio R
2 分数阶下加载面模型
基于本文提出的应力诱导分数阶剪胀方程,通过给定一个合理的下加载面硬化法则,可以直接建立适用于黏土的分数阶下加载面模型。
2.1 下加载面和硬化法则
根据Hashiguchi 等[24 − 26]的研究成果,本文假定下加载面与正常固结屈服面具有相似的几何形状,则下加载面屈服函数f可以表示为:


2.2 模型实现


2.3 参数试验
这里主要探究参数m的取值对模型计算结果的影响。首先将数值试样各向同性固结至800 kPa,然后卸载至100 kPa,从而形成OCR=8 的超固结试样。在此基础上分别选取不同的m的取值开展三轴压缩排水和不排水数值试验,模型参数如表1 所示。

表1 模型参数敏感性试验材料参数Table 1 Parameters used in model sensitive analysis
模型参数m对超固结重塑土的三轴压缩排水试验模型计算结果的影响如图4 所示。根据图4(a),该试样的峰值强度随着m值的增大而减小,体应变的剪胀量则逐渐增大。图4(b)给出了不同m值对材料剪胀曲线的影响,可以看出,随着m值的增大,该试样的剪胀应力比Md逐渐减小,而m不会对材料的临界状态剪应力比产生影响。
模型参数m对超固结重塑土的三轴压缩不排水试验模型计算结果的影响如图5 所示。根据图5(a),该试样的不排水抗剪强度随着m值的增大而减小,随着m值的进一步增大,材料的不排水抗剪强度甚至会小于其临界强度,该现象与密实砂土的应力-应变曲线变化特点具有某种相似性[22]。图5(b)给出了m对该试样的应力路径的影响。
3 模型验证
为了进一步验证本文所建立的分数阶下加载面模型的适用性,采用该模型分别对Black Kaolin黏土[39]和Fujinomori 黏土[29]的三轴压缩试验结果进行模拟,重点探究土体超固结性对其剪胀特性的影响,模型参数如表2 所示。
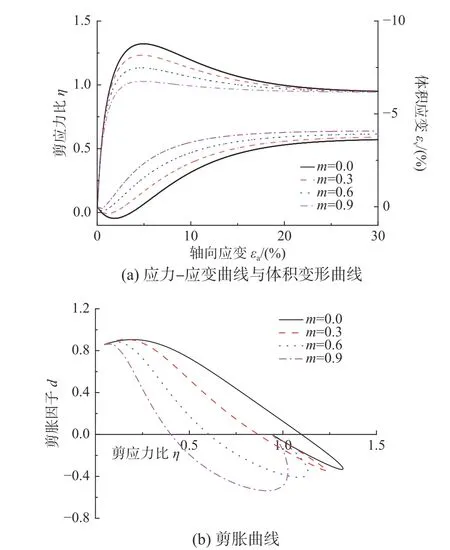
图4 参数m 三轴压缩排水试验模型计算结果的影响Fig. 4 Effect of parameter m on drained triaxial test model predictions

图5 参数m 三轴压缩不排水试验模型计算结果的影响Fig. 5 Effect of parameter m on undrained triaxial test model predictions
图6 给出了Black Kaolin 黏土的三轴压缩排水试验结果和模型计算结果,其中,Black Kaolin 黏土的加载围压分别为100 kPa、200 kPa、400 kPa和800 kPa,且OCR分别为8、4、2 和1。在不同的围压下,Black Kaolin 黏土的初始孔隙比e0分别为1.09、1.06、0.94 和0.91。根据图6(a)和图6(b),模型计算结果与试验结果具有良好的相关性。当OCR=8 时,由于应力历史的影响,Black Kaolin黏土的应力-应变曲线表现出明显的应变软化特点;在加载的初始阶段,土体的孔隙比e逐渐减小,产生剪缩变形,随着剪切破坏的进一步发生,e开始反向增加并伴随着剪胀现象的发生。Black Kaolin 黏土在不同围压下的剪胀曲线如图6(c)所示,可以看出土体的剪胀应力比Md随着OCR的增大而增大,同时在OCR=4,8 的情况下,土体会发生明显的剪胀变形。进一步,图7 给出了本文模型对Fujinomori 黏土的平均主应力一定的三轴压缩试验结果的模拟结果,其中,Fujinomori 黏土的平均主应力分别为98 kPa、196 kPa、196 kPa 和196 kPa,且OCR分别为8、4、2 和1。在不同的围压下,Fujinomori 黏土的初始孔隙比e0分别为0.727、0.713、0.76 和0.81。根据图7(a)和图7(b),可以看出本文模型能够较好的描述Fujinomori 黏土的应力-应变和体积变形特点。当OCR=8 时,本文模型计算得到的峰值强度所对应的轴向应变明显偏大,存在20%左右的误差,此时计算得到的体应变剪胀量也相应偏大。值得注意的是,相比常规的三轴压缩不排水试验,在平均主应力一定的情况下,模型计算得到剪胀曲线呈现出完全不同的变化特点。如图7(c)所示,在加载的初始阶段,剪胀因子d会逐渐增大,在达到峰值后反向减小,当OCR大于1 时,d会减小至负值,此时土体发生剪胀破坏,随着OCR的增大,该趋势将更加明显。

表2 模型参数敏感性试验材料参数Table 2 Parameters used in model sensitive analysis
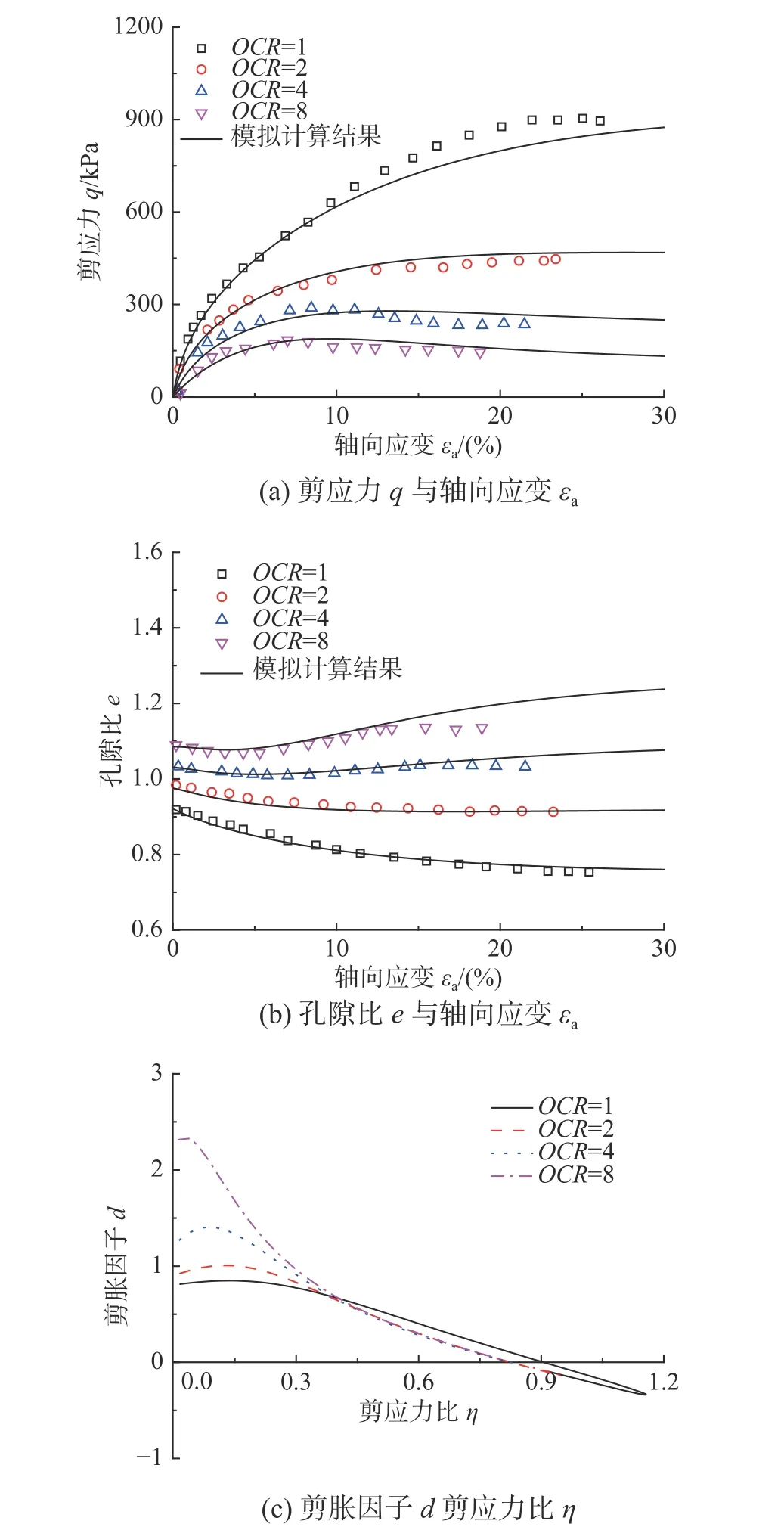
图6 Black Kaolin 黏土试验结果与模型计算结果对比Fig. 6 Comparison between experimental data and model predictions of Black Kaolin clay

图7 Fujinomori 黏土试验结果与模型计算结果对比Fig. 7 Comparison between experimental data and model predictions of Fujinomori clay
从上述分析可以看出,本文建立的模型能够合理地反映超固结重塑土的应变软化和剪胀特性,进而对土体应力-应变和体积变形特点进行准确的描述。此外,本文模型的计算结果表明,超固结性会对土体的剪胀特性产生影响。
4 结论
本文基于Caputo 微分方法提出了分数阶应力诱导剪胀方程以考虑超固结性对土体剪胀特性的影响,在此基础上引入了下加载面的力学概念,从而建立了适用于超固结重塑土的分数阶下加载面模型。通过将模型计算结果与试验结果进行对比分析,初步验证了该模型的合理性,主要结论有:
(1)基于 Caputo 分数阶微分方法,可以在不引入塑性势函数的情况下得到一个新的分数阶塑性流动法则,该流动法则能够合理地描述塑性流动方向与土体屈服面之间的非正交性,进而统一地描述相关联和非相关联的塑性流动法则。
(2)基于分数阶塑性流动法则,可以给出适用于黏土的分数阶应力诱导剪胀方程。由于分数阶数是关于表征超固结程度的相似因子的函数,因此本文提出的剪胀方程能够考虑超固结性对黏土剪胀特性的影响。
(3)通过引入下加载面的力学概念并且给出相应的硬化法则,本文所建立的分数阶下加载面模型能够准确地描述超固结黏土的应变软化和剪胀特性。相比较 MCC 模型,本文模型仅额外地引入了一个与土体剪胀特性有关的材料参数。
