环向对齐相邻缺陷管道失效压力研究

孙明明，李 昕

（1.郑州大学水利科学与工程学院，郑州 450001；2.大连理工大学a.海岸和近海工程国家重点实验室；b.工程抗震研究所，辽宁 大连，116024)

0 引 言

海底管道在服役过程中不可避免地受到腐蚀影响，导致管道壁厚减小，造成管道承载力下降。管道表面的腐蚀缺陷可以单独存在，也可以集中出现。每一个腐蚀缺陷都会改变缺陷内部和周围的应力和应变场，产生局部应力集中。对于影响区域重叠的两个或多个缺陷称为相邻缺陷。相邻缺陷群的失效行为比孤立缺陷的失效行为复杂得多。相邻缺陷间的相互作用对腐蚀管道的失效模式和承载能力有重要影响[1-3]，造成其内压承载力的下降，失效压力低于孤立缺陷的失效压力[4]。因此，有必要通过考虑缺陷相互作用的影响来评价相邻缺陷的内压承载力。

相邻缺陷之间的相互作用机理复杂，受到缺陷位置、缺陷尺寸和缺陷间距多个因素的影响。Li等[3]、Mondal等[1]和Chen等[5]对不同排列方式和不同缺陷尺寸的相邻缺陷的极限间距进行了研究，给出了相邻缺陷的判断方法；Sun 等[6-7]和Chouchaoui 等[8-9]对环向对齐相邻和轴向对齐相邻缺陷失效模式进行了分析，结果表明不同排列方式的相邻缺陷失效模式各不相同。有限元方法在相邻缺陷失效压力分析中得到广泛运用。Andrade 等[10]对含有相互作用腐蚀缺陷管道的有限元模型预测的失效压力和爆破试验结果进行了比较，证明了有限元方法的适用性；Benjamin 等[11]利用有限元方法对四种排列方式的相邻缺陷内压失效模式进行了研究，给出了不同间隔相邻缺陷失效模式的差异性；陈严飞等[12]基于非线性有限元方法，研究了X80管线与腐蚀缺陷相互作用时的失效行为，并建立了失效压力预测的评估方法；Elder Soares等[13]使用有限元模型研究了在内压和热载荷下，具有相互作用腐蚀缺陷管道的完整性；PETROBRAS 实验室进行了大量相邻缺陷的内压爆破试验，包括相同尺寸[4,14]和不同尺寸[15-16]缺陷组成的相邻缺陷，为相邻缺陷失效压力研究提供了试验数据库。

近30 年来，人们对腐蚀管道的内压失效机理和失效评估进行了深入的研究，建立了几种腐蚀管道剩余强度的计算方法。经典方法由一级评估方法组成，如ASME B31G 方法[17]、RSTRENG 085dL 方法[18-20]、DNV RP-F101 方法[21]和RPA 方法[22-23]。对于密集相邻缺陷，另一种方法是使用二级评估方法计算相互作用缺陷的失效压力。有两种二级评估方法被普遍采用[24]，其中2a 级评价方法用于评估孤立的复杂形状缺陷，例如RSTRENG 有效面积法[18-20]；2b级评价方法用于评估群腐蚀缺陷，例如用于相互作用缺陷的DNV RP-F101方法[21]和混合类型相互作用方法（MTI）[25]。考虑到缺陷长度、宽度和深度对破裂压力的影响，Chen 和Xin 等[26]提出了一种新的2b 级方法来预测具有相互作用缺陷的管道破裂压力。研究结果表明：对于相互作用的群腐蚀缺陷，2b 级方法提供了更精确的失效压力预测[4,11,25-28]；2b 级失效压力评价方法通过将相互作用缺陷转化为等效的单一腐蚀缺陷，并以分隔纵向间隔缺陷的全壁厚管道长度作为等效缺陷的长度。不同的2b级评估方法的主要区别在于等效深度的取值。

缺陷的排列和分布会影响到2b 级方法的评价结果，因此有必要对腐蚀缺陷排列方式进行分类。九十年代初，Kiefner 和Vieth[20]定义了腐蚀缺陷相互作用的三种基本类型。类型1 为环向分隔相邻且轴向投影重合的相邻缺陷，类型2 为轴向对齐相邻的缺陷，类型3 为由浅腐蚀缺陷和深腐蚀缺陷组成的不规则缺陷。研究表明，三种不同排列方式的相互作用缺陷的失效模式不同[2,6-9]。对于类型1中特殊的缺陷分布——环向对齐相邻缺陷，由于各个缺陷长度相同，相邻缺陷在轴向平面的投影完全重叠。因此，环向相邻缺陷数量的改变并不影响轴向投影和有效长度，现有的2b 级评价方法无法准确评估缺陷间相互作用对失效压力的影响。本文通过对环向对齐相邻缺陷特性和有效深度的研究，提出了一种更精确的该类型相邻缺陷的极限内压评估方法。

1 环向对齐相邻缺陷的评价方法比较

对于图1所示的相互作用缺陷（缺陷n到缺陷m），轴向投影和环向投影的有效深度分别定义为

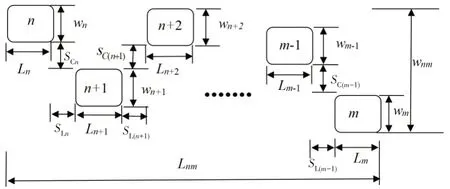
图1 相邻缺陷的几何尺寸Fig.1 Geometric dimensions of adjacent defects

式中：di、Li和wi分别为缺陷i的深度、长度和宽度；Lnm和wnm分别为有效长度和有效宽度；sLi和sCi分别为缺陷i和缺陷i+1的轴向和环向间距。

表1 环向对齐相邻缺陷的不同评价方法的区别Tab.1 Difference of evaluation methods for circumferentially-aligned defects

Leis和Stephens[29]认为缺陷宽度对极限内压载荷的影响不显著，因此大多数规范没有考虑缺陷宽度对失效压力的影响。根据相互作用的环向对齐相邻缺陷的特点，随着缺陷数目的增加，有效宽度增大，但是有效长度保持不变。因此有效深度是环向对齐相邻缺陷失效压力评估的关键因素。由于环向对齐相邻缺陷= maxdi(i=n,…,m) ＞，因此=＜maxdi(i=n,…,m)maxdi)＜maxdi(i=n,…,m)，= maxdi(i=n,…,m)。所有评价方法的有效深度都不大于相邻缺陷中的最大深度，所以失效压力的评估结果都会不小于相邻缺陷中最大深度缺陷的失效压力。这不仅无法评估相邻缺陷之间的相互作用造成的内压承载力的降低，而且高估了管道的承载力，评估结果偏危险，容易引发管道内压失效事故。

2 环向对齐相邻缺陷有效深度的计算

有效深度是环向对齐相邻缺陷失效压力评估的关键因素。根据2b 级评价方法中有效深度的表达式，可知相互影响的群腐蚀的有效深度dnm均为轴向有效深度、环向有效深度和体积有效深度的某一种或者某两种的组合。因此考虑采用、和为自变量的函数作为dnm的表达式。

式中，f()为自变量、和的某种函数表达式。

对于相邻缺陷之间的相互作用，主要受缺陷间距和缺陷尺寸的影响[3]。f(,,)表征了缺陷间距和尺寸对有效深度的影响。为得到有效深度式（3）的具体表达式，需要得到有效深度的真实值，以此确定式（3）中的表达式。根据DNV-RP-F101（Interaction）[21]和MTI[25]，采用DNV-RP-F101（单点）评估方法计算等效缺陷的失效压力，并以此为基础计算相邻缺陷有效深度的真实值。

式中，pf为相邻缺陷的失效压力，σu为工程抗拉强度，p0为完好管道的失效压力，Qnm为等效缺陷的长度修正系数。

由式（4）～（6）可知，知道相邻缺陷的失效压力pf后，可以得到真实有效深度dnm，代入式（3）中可以拟合得到有效深度的表达式。为丰富环向对齐相邻缺陷失效压力数据，决定采用有限元方法对不同尺寸和不同排列方式的环向对齐相邻缺陷的失效压力进行计算。

3 环向对齐相邻缺陷管道数值分析

3.1 有限元模型的建立

为了研究环向间距对环向相邻缺陷的失效压力的影响，建立了含有两个环向对齐相邻缺陷的钢制管道有限元模型。采用通用有限元软件ANSYS 对腐蚀管道的失效行为和极限内压承载力进行了有限元分析。考虑到pf/p0是与钢材强度等级无关的无量纲参数[30-32]，由式（5）可知有效深度dnm与钢材强度等级无关，因此有限元模型仅针对单一的钢材强度进行计算。以Benjamin的试验为参考，管道材料为API-5L-X80[4-14]。真实应力-应变曲线由Ramberg-Osgood模型进行模拟，如式（7）所示：[10-11]

实测得到的材料性能为屈服强度σy=534.1 MPa，真实极限抗拉强度σu,ture=718.2 MPa.。弹性模量（E）为200 000 MPa，泊松比（v）为0.3。X80的真实应力应变曲线如图2所示。

图2 X80 钢材真实应力应变曲线Fig.2 True stress-strain relationship of API X80 pipeline steel

管材模型外径D和壁厚t分别为458.8 mm和8.1 mm。采用20 节点六面体实体单元SOLID 45 建立有限元模型。由于对称性，只有四分之一的钢材模型被建立，如图3所示。缺陷沿厚度方向分为四层，在远离缺陷的地方单元被减小到一层。缺陷环向切分成14 份，轴向切分成12份，单元径向最小厚度为0.6 mm，最大厚度为8.1 mm。管道模型长度为1000 mm≈2.2D，以防止边界条件影响相关区域的应力。为了减小应力集中效应，对缺陷进行了倒角处理。腐蚀缺陷假定为具有光滑边缘的矩形，边缘进行倒角处理，倒角半径为3.5 mm。为了验证有限元模型的网格是否足够精细，进行了网格收敛性研究。

图3 缺陷管道的有限元模型Fig.3 FEM of the corroded pipeline

3.2 计算工况说明

根 据ASME B31G 标 准[33]和Modified B31G 标 准[19-20]，将 缺 陷 长 度 范 围 位 于L/Dt＜ 20Dt、20Dt≤L/Dt＜ 50Dt和L/Dt≥ 50Dt的腐蚀缺陷分别定义为短腐蚀缺陷、长腐蚀缺陷和超长腐蚀缺陷。Colony 1c-Colony 5c 分别由两个环向对齐相邻的Basic 1c-Basic 5c 缺陷组成。表2 列出了基础缺陷工况（Basic 1c-5c）和环向相邻缺陷工况（Colony 1c-5c）的几何参数。基础缺陷工况是仅包含一个缺陷的管道工况，其中Basic 1c-2c为短腐蚀缺陷，Basic 3c-4c为长腐蚀缺陷，Basic 5c为超长腐蚀缺陷。d/t取值0.3、0.5和0.67分别代表浅腐蚀缺陷、中度腐蚀缺陷和重度腐蚀缺陷。分别采用环向宽度为8°（w=31.9 mm）和18°（w=72.1 mm）的缺陷来表示狭窄缺陷和正常缺陷[7]。

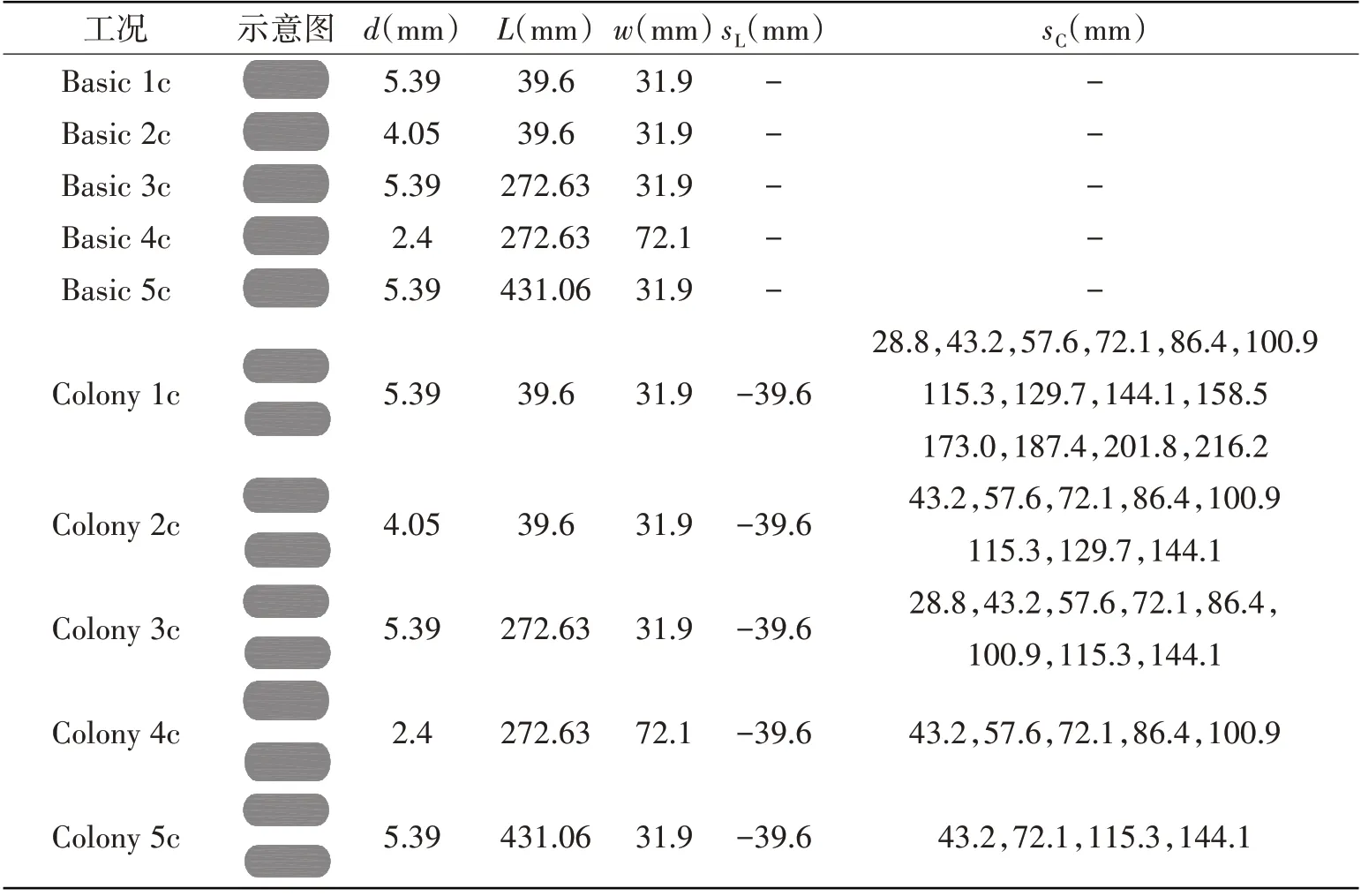
表2 群腐蚀参数Tab.2 Parameters of colonies

必须说明的是，本文模拟的腐蚀缺陷尺寸均在管道实际缺陷的尺寸范围之内。根据AGA/PRCI腐蚀管道试验数据库[2,21]，管道上检测得到的实际腐蚀缺陷的长度范围为19.35～3048.00 mm，最大缺陷深度1.60～17.10 mm，宽度为0.15～304.80 mm[34]。本文计算工况模拟的腐蚀缺陷长度为39.6～431.06 mm，最大缺陷深度为2.4～5.39 mm，宽度为31.9～72.1 mm。

3.3 有限元分析结果

表3 列出了五种基础缺陷下的失效压力。附录A 给出了Colony 1c-Colony 5c 的失效压力以及每种群腐蚀工况的失效压力pf与之相应的基础工况的失效压力（pf）BC之比。基于两者的失效压力比值，可以得到Colony 1c-Colony 5c 内缺陷之间的相互影响程度。这里假定当此比值pf/（pf）BC等于或大于0.99 时，相邻缺陷之间没有相互作用。比较附录A中给出的失效压力可以看出，对于相互作用的双点环向相邻工况（CA21-CA25），影响环向相邻缺陷失效压力和相互作用的主要有两个因素：

表3 基础工况的失效压力Tab.3 Failure pressures of the basic cases

（1）环向间距

对于所有工况，环向间距减小，缺陷高应力区接近，缺陷之间的相互作用增加。

（2）缺陷长度

①对于超长腐蚀缺陷L≥，不存在相互作用。CA25算例无相互作用算例。

（3）缺陷深度

对于短腐蚀缺陷算例（CA21-CA22），CA21 算例（d/t=0.67）环向极限距离为144 mm，远大于CA22算例（d/t=0.5）环向极限距离100 mm。而且对于相同环向距离的相邻缺陷，CA21算例的pf/（pf）BC值均小于CA22 算例。长腐蚀缺陷算例（CA23-CA24）也有相同规律。由此可知，随着缺陷深度的增加，环向相邻缺陷的相互作用程度逐渐增加。

4 环向对齐相邻缺陷有效深度的确定

4.1 环向对齐相邻工况的有效深度

选择有相互作用的环向对齐相邻工况的有效深度，去掉无相互作用的工况。根据表1，三个主要的有效深度基本表达式是、和，这三个参数分别列在附录B 中。有效深度dnm采用式（2）、（4）～（6）进行计算。图4是环向对齐相邻缺陷的不同有效深度的比较。从图4 中可以看出，由于所有工况中只考虑了环向间距的变化，且轴向间距不变，因此在同一类型群腐蚀缺陷中，轴向投影的有效深度不发生变化。对于两个环向对齐相邻缺陷组成的群腐蚀缺陷工况（CA21、CA22、CA23和CA24），环向投影的有效深度和体积有效深度相同，真实有效深度dnm更接近轴向有效深度且大多数情况下大于其它三种评价方法的有效深度、和。因此导致现有评估方法在预测环向对齐相邻群腐蚀缺陷失效压力时结果更为危险。

图4 不同有效深度对比Fig 4 Contrast of different effective depths

4.2 不同有效深度相关性分析及误差分析

为更好地得到真实有效深度的计算方法，需要对各种不同有效深度与真实有效深度dnm的相关性进行研究。选取以下几个参考深度进行相关性分析：（1）；（2）；（3）d1/2=/2+/2;（4）；（5）轴向等效深度和环向等效深度较小值dmin= min(,)；（6）轴向等效深度和环向等效深度较大值dmax= max()。

表4 为不同参考指标与真实有效深度的相关系数对比，以及以式（7）为基础，采用不同参考指标预测环向相邻缺陷失效压力的误差对比。由表4中可以看出，对于环向对齐相邻缺陷，与真实有效深度相关度大于90%的为d1/2、dmax和，误差最小的是和dmax。

表4 不同参考指标与真实有效深度的相关系数和误差对比Tab.4 Comparison of correlation coefficients between reference indexes and true effective depth

4.3 环向对齐相邻缺陷有效深度拟合

由此可见，对于环向对齐相邻群腐蚀情况，有效深度主要与两种参考标准有关：轴向等效腐蚀深度，轴向等效深度和环向等效深度较大值dmax。有效深度与该参数相关性最高，且误差最小。对于环向对齐相邻缺陷，=dmax，因此采用为自变量，即

为了得到有效深度的计算方法，回归拟合方程采用以下标准进行选择：

（1）拟合方程在自变量区间内呈现单调变化。

（2）对于极端上限情况，当自变量为管壁厚度8.1 mm 时，即缺陷穿透整个管壁厚度，实际等效深度也为8.1 mm，故增加（8.1，8.1）个数据点。

（4）为增加拟合公式的适用性，对不同参考指标进行深度归一化处理。归一化后的拟合公式针对不同腐蚀程度的管道都会对应一个等效深度的无量纲化参数，不会因为管道壁厚的改变而造成拟合公式的不适用性。令等效深度的无量纲化参数αeff=，轴向等效深度无量纲化参数αaxi=。

将参考标准归一化之后，表5为两种自变量的拟合结果。

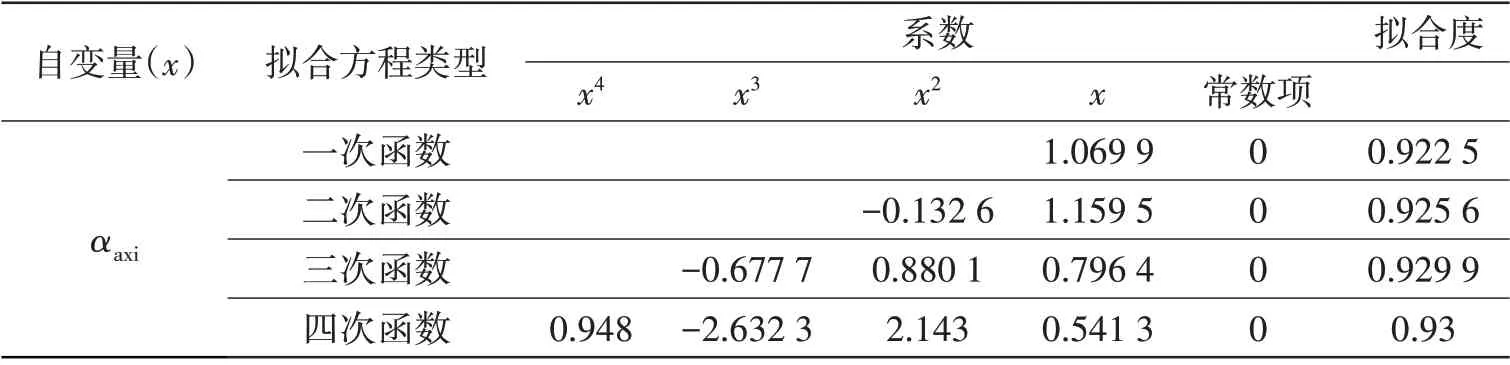
表5 不同自变量的拟合结果Tab.5 Fitting results of different independent variables

表6为采用不同单变量拟合结果进行失效压力预测时误差绝对值的平均值对比。由表中可以看出，以为参考指标拟合得到的回归方程用来预测群腐蚀管道失效压力时，四种方程误差基本相同，说明以为自变量，反演真实等效深度为因变量的函数关系较为稳定，不会因为拟合函数的改变而发生较大变化。

表6 不同拟合结果预测失效压力误差对比Tab.6 Comparison of errors in predicting failure pressure with different fitting results

在单变量回归方程中，考虑到以daxinm为参考指标拟合得到的截距为0 的一次函数回归方程用来预测群腐蚀管道失效压力的误差最小，而且计算简便，决定采用截距为0 的一次函数拟合方程作为最终拟合结果。图5 为拟合曲线，无量纲化参数αeff单变量回归方程的拟合结果如式（9）所示。

图5 等效深度拟合曲线Fig5 Effective depth fitting curve

将式（9）得到的有效深度dnm代入式（4），即可得腐蚀管道的失效压力。

5 评价方法的验证

Chouchaoui 和Pick[9]和Benjamin 等[4,14]分别对环向相邻缺陷的X46 和X80 管道进行了一系列爆破试验。考虑到二者的实验是针对低强度钢（X46）和高强度钢（X80），且环向对齐相邻缺陷中的单个缺陷形状相同。然而，实际管线腐蚀缺陷形状较为复杂，需要对含有不同缺陷尺寸的环向相邻腐蚀缺陷进行研究。大连理工大学结合自主研发的管道复杂荷载试验机对X52钢材进行了不同环向相邻工况的内压爆破试验研究，该试验包括不同尺寸的相邻缺陷内压失效试验[35]。

为了验证环向对齐相邻缺陷有效深度拟合公式的准确性，不同计算方法的计算误差如表7所示。从表中可以看出，不同钢材等级下本文方法的最大误差、最小误差和平均值均最小。在现有的主要评价方法中，以轴向有效深度作为环向对齐相邻缺陷有效深度的DNV-RP-F101 方法最为准确，以体积有效深度或环向有效深度作为有效深度的MTI 方法的误差最大。本文方法的误差仅为DNV-RPF101方法误差的1/3。

表7 不同方法预测失效压力的误差比较Tab.7 Comparison of errors in predicting failure pressure with different methods

6 结 论

本文结合环向对齐相邻缺陷失效压力的有限元计算结果，提出了一种改进的环向对齐相邻缺陷有效深度计算方法，得出以下结论：

（1）环向对齐相邻缺陷之间的相互作用主要取决于环向间距、缺陷长度和缺陷深度。如环向间距和缺陷长度的增加或缺陷深度的减小，则相邻缺陷之间相互作用减弱。

（2）环向对齐相邻缺陷和复杂分布缺陷的失效压力变化规律不同，腐蚀管道应分别考虑缺陷环向对齐相邻和复杂分布情况。对于环向对齐相邻缺陷管道的失效压力评估，DNV-RP-F101是现有三种2b级评估方法中误差最小的方法，而MTI评估方法的误差最大。

（3）与Chen and Li、DNV-RP-F101和MTI等失效压力评估方法相比，本文方法对于环向对齐相邻缺陷失效压力的预测，其精度有大幅度提高。

“CA2120”代表“环向对齐”、“2个腐蚀缺陷”、“基础缺陷为Basic1c”和“SC=20 mm”的工况。

Case 是否有相互作用Colony 1c Colony 2c Colony 3c Colony 4c Colony 5c CA2128 CA2143 CA2157 CA2172 CA2186 CA21100 CA21115 CA21129 CA21144 CA21158 CA21173 CA21187 CA21201 CA21216 CA2243 CA2257 CA2272 CA2286 CA22100 CA22115 CA22129 CA22144 CA2328 CA2343 CA2357 CA2372 CA2386 CA23100 CA23115 CA23144 CA2443 CA2457 CA2472 CA2486 CA24100 CA2543 CA2572 CA25115 CA25144 28.8 43.2 57.6 72.1 86.5 100.9 115.3 129.7 144.1 158.5 173.0 187.4 201.8 216.2 43.2 57.6 72.1 86.5 100.9 115.3 129.7 144.1 28.8 43.2 57.6 72.1 86.5 100.9 115.3 144.1 43.2 57.6 72.1 86.5 100.9 43.2 72.1 115.3 144.1 18.00 18.24 18.49 18.80 19.12 19.39 19.71 20.11 20.39 20.69 20.69 20.70 20.70 20.70 20.14 20.38 20.66 20.96 21.22 21.50 21.67 21.70 8.56 8.78 8.92 9.06 9.14 9.28 9.54 9.63 17.66 17.88 17.98 17.98 17.99 8.8 8.8 8.8 8.8 0.870 0.881 0.893 0.908 0.924 0.937 0.952 0.971 0.985 1.000 1.000 1.000 1.000 1.000 0.928 0.939 0.952 0.966 0.978 0.991 0.999 1.000 0.889 0.912 0.926 0.941 0.949 0.964 0.991 1.000 0.981 0.993 0.999 0.999 1.000 1.000 1.000 1.000 1.000是是是是是是是是是否否否否否是是是是是否否否是是是是是是否否是否否否否否否否否工况sC（mm）pf（MPa）pf/（pf）BC

附录B：环向对齐相邻工况的不同有效深度

工况daxi dcir dMTI Colony 1c Colony 2c Colony 3c Colony 4c CA2128 CA2143 CA2157 CA2172 CA2186 CA21100 CA21115 CA21129 CA21144 CA2243 CA2257 CA2272 CA2286 CA22100 CA2328 CA2343 CA2357 CA2372 CA2386 CA23100 CA2443 dnm(mm)6.51 6.42 6.32 6.18 6.02 5.86 5.64 5.32 5.06 5.08 4.81 4.44 3.96 3.44 5.80 5.73 5.69 5.64 5.62 5.57 2.33 nm(mm)5.39 5.39 5.39 5.39 5.39 5.39 5.39 5.39 5.39 4.05 4.05 4.05 4.05 4.05 5.39 5.39 5.39 5.39 5.39 5.39 2.40 nm(mm)3.71 3.21 2.83 2.53 2.29 2.09 1.92 1.78 1.65 2.41 2.13 1.90 1.72 1.57 3.71 3.21 2.83 2.53 2.29 2.09 1.85 nm(mm)3.71 3.21 2.83 2.53 2.29 2.09 1.92 1.78 1.65 2.41 2.13 1.90 1.72 1.57 3.71 3.21 2.83 2.53 2.29 2.09 1.85