高中生数学抽象素养培养的实践研究

胡昌亮

[摘  要] 抽象素养的第二和第三水平的高低直接影响着学生解决中档题和综合难题的能力. 笔者以自己的课堂教学实践为背景，刍议了抽象素养培养的两个途径：层第性培养学生的抽象素养;利用课堂的生成性发散思维提升抽象素养.

[关键词] 抽象素养;层第性培养;发散思维;阅读素养

新的课程标准中，描述了高中数学核心素养的六个主要方面，即数学抽象、逻辑推理、数学建模、运算能力、直观想象和数据分析，并从概念的界定，及其在数学与生活中的作用和意义方面进行了描述. 在素养之一的数学抽象中，便指出数学抽象是指舍去事物的一切物理属性，得到数学研究对象的思维过程. 给出数学抽象的作用是使得数学成为高度概括、表达准确、结论一般、有序多级的系统.

在现实教学过程中，学生可以根据熟悉的情境直接抽象出数学问题，形成解决问题的思路和方法，可是遇到稍微难的题目，就会出现抽象障碍，这类题目，即新课标中关于抽象素养的三个水平维度的第二和第三水平：联系和创造. 如何高效地培养学生的抽象素养是一线教师需要深究的.

层第性培养学生的数学抽象素养

学生的学习不是一蹴而就的，这需要我们教师在教学过程中循序渐进地引导，形成系统性的解题经验. 下面笔者以导数与函数单调性的关系为背景，从4个水平维度阐述如何层第性培养学生的抽象思维品质.

水平1（导函数可解可作图型）：函数f（x）=（x2+2x）ex（x∈R）的单调递减区间为__________.

评价：这是较简单的一类函数单调性求解题型，求导后解不等式即可. 但直接解不等式得出单调区间毕竟是非区分题，对于压轴题，并不能直接解决. 实际上不等式的解集反映在图像之上，即为x轴的上方或下方部分对应的自变量范围，所以只要能作出导函数中符號可变部分的大致图像，如本题中的y=x2+4x+2，再结合零点，就可求出单调区间. 这样以形助数，抽象思维与形象思维相结合，可以为后面的深度学习打下扎实的基础.

水平2（导函数可猜零点型）：函数f（x）=ex+■x2-（2+ln2）x的增区间为____.

评价：函数求导后，由于不会求导函数的零点，学生可能解不出不等式，但导函数单调性仍可判断，故可引导学生猜出零点. 由于导函数的表达式出现了ex及ln2，根据指数函数与对数函数的关系可猜零点为x=ln2，作出草图，数形结合即可求出单调性.

水平3（导函数零点可设型）：函数f（x）=e2x-alnx. 证明：当a>0时， f（x）≥2a+aln■.

评价：求导后导函数的零点不可求或者不可猜，但能判断其零点存在，考虑设出导函数的零点，并得到函数的最小值，则有f（x）≥f（x0）=e■-alnx0. 教师之后引导学生利用2e■-■=0将e■-alnx0化简为f（x0）=e■-alnx0=2ax0+■+aln■，再利用基本不等式即可得出结果. 经此，学生后面遇到类似问题会有两方面的意识：一是零点不能求仍然可以设出来;二是可以利用零点满足的方程，将最值表达式中的指数、对数式子化简为不含指数、对数背景的表达式.

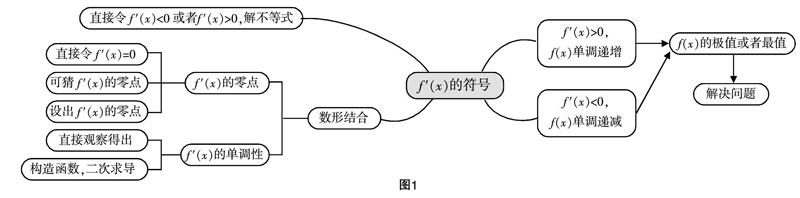
水平4（二次求导型）：若函数f（x）=■，0

评价：本题只要能判断出函数f（x）在（0，π）内的单调性即可. 学生求导后，亦可猜出零点，但由于f ′（x）的单调性无法判断，这是本题的思维障碍点. 此时引导学生为判断f′（x）的单调性，构造函数g（x）=xcosx-sinx并求导，可判断g′（x）为负，即f ′（x）单调递减;由f′（0）=0，可知f ′（x）在（0，π）上恒负，所以函数f（x）在（0，π）内递减，即a>b.

图1是4个水平层次的思维导图，由浅入深螺旋递进，学生层第性解决每个水平上的思维障碍点，获取知识的本质，提高自身的抽象素养.

有效利用课堂上学生的生成性发散思维，因势利导解决问题

众多学者所写的关于发散思维的论文比较集中在“一题多解”上，笔者在此不再赘述，此处笔者想谈一下怎样利用课堂上自然生成的发散思维来达到提升抽象素养的目的.

在函数不等式问题中，经常需要构造函数，由“导”寻“源”，解决问题. 比如下面一道选择题：

（单选）已知函数f（x）是定义在（0，+∞）上的非负可导函数，且满足xf′（x）+f（x）≤0，对于任意正数a，b，若a

A. af（a）≤f（b） B. bf（b）≤f（a）

C. af（b）≤bf（a） D. bf（a）≤af（b）

由“导”寻“源”，学生构造函数g（x）=xf（x），则g′（x）=f（x）+xf′（x）≤0，所以g（x）=xf（x）为（0，+∞）上的减函数. 因为ag（b），即af（a）>bf（b）. 但选项中没有此答案，可学生的解法又没有问题，怎么办？教师此时应该对学生的这种发散思维方式予以肯定，同时因势利导：若此题加上这个答案，就会变成多选题，契合了新高考. 然后可利用这种难得的课堂生成，引导学生思考没找到答案的原因：通过观察选项C和D，若能解决f（x）的单调性进而判断出f（a）与f（b）的大小即可. 此时由条件xf′（x）+f（x）≤0，可知f′（x）≤-■≤0，所以f（x）为（0，+∞）上的减函数，即有f（a）>f（b）≥0，又0

学生课堂生成性的发散思维有多个来源，上面显然就是因为学生思维的起点不同而出现的解题方式. 作为教师，应该利用好课堂上宝贵的生成性资源，理清思路，肯定学生，课堂氛围民主，学习才能高效，抽象素养也才能随之得到培养.

学生的抽象素养并不是依靠口头的传授，更不是通过题海战术获得，它需要我们在平时的教学中，层第性地去启发，同时抓住课堂上的思维闪光点作为我们的教学素材. 最后，希望笔者的一点点教学实践可以给广大教师带去一些思考.