基于多级混合澄清槽的PUREX流程的计算模型

汤 嘉，郭子方，翁汉钦，林铭章,2,*

1.中国科学技术大学 物理学院 工程与应用物理系，安徽 合肥 230026；2.中国科学技术大学 核能安全技术研究院，安徽 合肥 230031

核能作为我国替代石油等不可再生能源的主要能源之一，已成为我国重点发展的能源类型[1]。而核能的发展会产生大量的乏燃料。乏燃料中主要含有U、Pu等可再利用的元素以及少量次锕系元素和裂片元素。其中，若实现对所有Pu的回收和再利用，即可将乏燃料的放射毒性降低10倍[2]。合理处理乏燃料不仅有利于核能的可持续发展，也有助于生态稳定。目前，以磷酸三丁酯(TBP)为萃取剂的PUREX流程已应用于乏燃料后处理过程。PUREX流程由多个循环流程构成，主要包含铀钚共去污分离循环、铀的净化循环和钚的净化循环三个流程。这些流程通过利用萃取剂对不同价态元素的萃取性能的差异，实现元素的分离和纯化。

在PUREX流程中，价态调节是影响最终产品液纯度和回收率的关键因素之一，因此还原剂和支持还原剂的选择和用量直接影响萃取效果。由于金属离子在TBP中的分配系数与酸碱性有关，所以酸度的选择也会影响萃取效率。PUREX流程中产生的辐射以及溶解铀芯的过程均会促使HNO3生成HNO2，而HNO2会改变Pu和Np的价态，影响Pu和Np在萃取流程中走向。此外，流比的选择、料液中待分离组分的浓度均会对萃取造成影响。因此确定合理的流程参数成为提高PUREX流程萃取效率的关键。在工程应用前，以上工艺参数等均需通过热试验获得。由于铀钚分离过程影响因素众多，在热试验前通过采用数值计算方法进行计算机模拟，可为热试验缩小参数的选取范围。对PUREX流程的数值模拟可提高热试验效率，降低热试验成本，因此具有重要意义。

近年来，模拟PUREX流程的计算程序相继被开发出来，如法国原子能和替代能源委员会(CEA)开发的PAREX[3]，德国技术化学所开发的VISCO[4]，日本核燃料循环发展研究所(现JAEA)开发的MIXSET-X[5]，日本原子能机构开发的PARC[6]等。近20年来，我国中国原子能科学研究院(下文简称原子能院)等少数单位在开展相关研究。原子能院目前已经开发了模拟混合澄清槽中U、Pu萃取行为的程序[7-8]，基于该模型，进一步引入Zr、Nb、Ru等裂片元素的萃取模型，即可对PUREX的共去污流程进行数值模拟。后续原子能院又开发了引入一个化学反应的单级混合澄清槽模拟程序[9]。而在实际的PUREX流程中，多个化学反应会同时进行，且各物质的浓度会随着水相和有机相的反向流动在多级串联的混合澄清槽中发生变化。因此原子能院的该程序距实际的PUREX流程模拟还有一定的差距。基于这样的背景下，本工作拟建立多级混合澄清槽模型，并在该模型的基础上建立涉及萃取过程和多个化学反应的计算机模型，用于模拟各级混合澄清槽中物质达到稳态时的浓度。

1 PUREX流程数学建模过程

在PUREX流程中，化学反应的发生、两相浓度未达到萃取平衡以及水相和有机相的动态流动均会使两相中的各物质产生浓度变化。基于以上三点，模拟PUREX流程需要获取各组分的分配比和化学反应数据(反应方程、化学反应速率常数)，并建立分配比模型[5,8,10]、化学反应模型、传质模型。

1.1 化学反应模型和算法

对于反应物为M和N、生成物为P和Q的反应，其通式为：

mM+nN=pP+qQ

(1)

其中，m、n、p、q分别为M、N、P、Q的化学计量系数。

设定该化学反应的反应速率常数为k，则物质M的微分表达式为：

(2)

若系统中物质M参与W个反应，则物质M的微分表达式可表示如下：

(3)

其中：Δi为i反应的各反应物浓度的系数次幂之积；M为反应物时，b为1，M为生成物时，b为0。

可通过式(3)得到反应体系内所有物质的微分方程，通过对时间的积分，即可得任意时刻的物质浓度。但不同反应的化学反应速率存在较大的差异，在数学处理过程中存在难度。如在PUREX流程中的铀钚分离工艺(1B)的初始时刻，存在两个反应速率相差较大的反应：

2Pu(Ⅳ)+2NH3OH+=

2Pu(Ⅲ)+4H++N2+2H2O

(4)

2Pu(Ⅵ)+HNO2+H2O

(5)

以下是常见的常微分方程的初值问题：

(6)

y(x0)=y0

(7)

其中x0≤x≤x1。

用一阶BDF算法(也称向后欧拉法)求解yn+1的表达式为：

yn+1=yn+hf(xn+1，yn+1)

(8)

其中h为单次步长。由以上知，yn+1的表达式中含有yn+1，因此需要通过迭代解此方程。该算法的总体截断误差为O(h)。

用二阶BDF算法(也称梯形公式法)求解yn+1的表达式为：

(9)

(10)

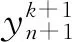
BDF算法最高有五阶，阶数越大，复杂度越高。可通过设置更高的阶数以牺牲计算效率实现截断误差的降低。为了增加计算精度，本工作在计算中使用五阶BDF算法。程序的实际运算时长小于600 s。

1.2 传质模型

1) 单级传质模型

在混合澄清槽的混合室内，水相和有机相中均会有化学反应发生。由于某些关键物质如羟胺(HAN)等，微溶或不溶于有机相，使得有机相中的化学反应比水相中的要少。此外，TBP粘性较大，使得有机相中物质的传质系数降低，化学反应速率下降。对于化学反应：

2Np(Ⅴ)+4H+

(11)

有机相中的化学反应速率常数只有水相中的1/8 000[5]。由于混合澄清槽中存在机械搅拌的物理过程，也促进了物质在两相中的传质速率。基于以上事实，本工作简化计算流程，做出如下假设:

(1) 化学反应仅发生在混合室，且化学反应仅在水相中进行；

(2) 传质是一个非稳态过程。

单级传质模型的示意图示于图1。

方框中红线左侧为水相，红线右侧为有机相，红圆表示氧化性物质，蓝圆表示还原性物质，蓝色双箭头表示化学反应，红色双箭头表示传质过程图1 单级混合澄清槽的传质模型(简化)Fig.1 Mass transfer model of one-stage mixer-settler(simplified)

2) 多级分液漏斗模型

在PUREX流程中，混合澄清槽是由多个单元串联而成。可通过分液漏斗的多次操作来模拟这一过程。两端进料的分液漏斗模型可参考文献[8]，中间进料的分液漏斗模型示于图2。

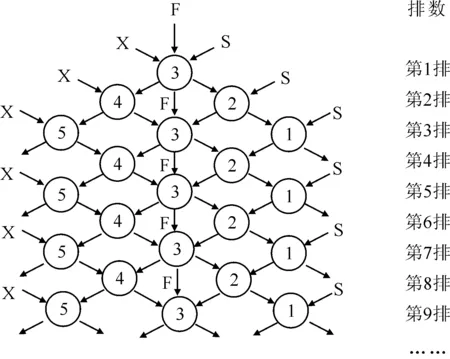
F表示料液，X表示萃取液，S表示洗涤液图2 5级混合澄清槽的中间进料的分液漏斗模型示意图Fig.2 Process of separating funnel model standing for 5-stage mixer-settler feeding at middle stage

中间加料的多级分液漏斗模型与两端加料的多级分液漏斗模型流程略有不同。在每次对中间加料的分液漏斗进行操作时，需要加入包括料液、萃取液和洗涤液在内的三类液体。分液漏斗按图2所示方向加料，振荡，静止分相。两相在分液漏斗里充分混合和反应后，其走向按照图中指向转移到下一个分液漏斗。

从理论上讲，要经过多次多排振荡分离后，才能使得漏斗两相中各物质的浓度达到稳态。大量实践表明，一般操作排数大于或等于混合澄清槽级数的三倍时，就接近稳定的浓度值[17]。

3) 体积膨缩效应模型

溶液中溶质浓度的改变会引起体积的变化，分子量大的物质对溶液体积的影响更为显著。由于乏燃料中的U、Pu、硝酸等浓度较高，因此必须考虑溶液的体积膨缩效应[8]。

典型轻水反应堆(LWR)的高放废液中的裂片元素质量浓度均不超过2 g/L[18]，因此计算水相的体积膨缩效应时，仅考虑U、Pu和硝酸对体积的影响。此外，TBP能溶解水，TBP在有机相中的比例越高，溶解水的能力越强，30%(体积分数，下同)TBP的有机相溶解的水最多可达约0.4 mol/L[19]。在计算有机相的体积膨缩效应时，除考虑U、Pu、硝酸的影响外，还需要考虑水的影响。

需要注意的是，对于中间进料的工艺流程，在料液进料口，料液和洗涤液两种不同离子浓度水相会相互混合。根据体积膨缩效应，水相的混合不会改变总体积，因此该模型仅需应用于水相与有机相之间的离子交换过程。

2 模型可靠性验证

铀钚分离是PUREX流程的关键工艺，Pu的调价是决定这一工艺的关键。此外，Np作为重要性仅次于U、Pu的元素(可用于制造238Pu等)，使得Np的走向控制也是PUREX流程中重点研究方向。因此用以上数学模型建立的计算模型对硝酸羟胺(HAN)还原Pu(Ⅳ)的过程和Np的萃取实验进行验证，实验数据来自于MIXSET-X[5]。以上元素均具有放射性，会使得水溶液体系发生辐解反应[20-21]，但基于单流程时长较短且辐射强度较低，暂不考虑水溶液的辐解。

2.1 HAN还原Pu(Ⅳ)的验证

混合澄清槽为8级串联，含有Pu(Ⅳ)的有机相和含有HAN及肼(HYD)的水相分别从两侧进料，在混合澄清槽中接触并发生反应，最终Pu(Ⅳ)被转化成为Pu(Ⅲ)并进入水相。料液浓度和流程示意图示于图3。

图3 HAN还原Pu(Ⅳ)的两端进料的8级混合澄清槽流程图Fig.3 Reduction process of Pu(Ⅳ) by HAN with 8-stage mixer-settler feeding at end stage

此过程水相中发生的化学反应列于表1[5,21]。

图4(a)和图4(b)分别展示了MIXSET-X和MPMS的计算值与实验数据的对比。在进料端附近，MIXSET-X和MPMS的计算结果均与实验值较为吻合。但在远离进料端时，对比MIXSET-X和MPMS的模拟结果，MIXSET-X的计算值与实验值偏离较大。

表1 HAN还原Pu(Ⅳ)过程中发生的化学反应[5,21]Table 1 Reactions of reduction process of Pu(Ⅳ) by HAN[5,21]

2.2 Np萃取实验的验证

在16级混合澄清槽中，从第8级引入U(Ⅳ)和HYD与Np发生化学反应，改变Np的价态，从而影响Np的萃取状态。料液从中间进料，两侧各自通入有机相和洗涤液。料液浓度和流程示意图示于图5。

图4 MIXSET-X(a)与MPMS(b)的计算值分别与HAN还原Pu(Ⅳ)的实验值的对比Fig.4 Calculated results of MIXSET-X(a) and MPMS(b) compared with experimental values of reduction process of Pu(Ⅳ) by HAN respectively

图5 萃取Np过程的中间进料的16级混合澄清槽流程图Fig.5 Extraction process of Np with 16-stage mixer-settler feeding at middle stage

此过程水相中发生的化学反应列于表2[5]。

表2 Np在萃取过程中发生的化学反应[5]Table 2 Reactions of Np in extraction process[5]

图6(a)和图6(b)分别展示了MIXSET-X和MPMS的计算值与实验数据的对比。MPMS的计算值整体上更加接近实验值，有机相Np的计算值与实验值能较好地匹配。在9—16级单元，MIXSET-X的计算值与实验值偏离较大。

2.3 讨论

从图5和图6可以看出，在混合澄清槽的进料单元附近，Pu和Np的计算值和实验值具有较高的吻合度。在远离进料单元时，计算值均偏离实验值，且误差逐渐扩大。对比MIXSET-X在远离混合澄清槽进料单元处的计算值，MPMS的计算值与实验数据更为吻合。如MPMS和MIXSET-X分别模拟计算HAN还原Pu(Ⅳ)的过程：在第6级混合澄清槽单元中，水相Pu(Ⅲ)质量浓度对应的计算值分别为0.045 g/L(MPMS)和1.60×10-5g/L(MIXSET-X)，相差约280倍。

远离进料单元处的计算误差较大。推测原因为该体系中化学反应的反应速率多是经验或半经验公式，这使得计算过程中产生不可消除的误差。误差在混合澄清槽多级单元中不断累积，最后使得远离进料单元处的误差呈现指数扩大。并推测这是误差产生的主要来源。

图6 MIXSET-X(a)和MPMS(b)的计算值分别与Np萃取的实验值的对比Fig.6 Calculated results of MIXSET-X(a) and MPMS(b) compared with experimental values of Np in extraction process respectively

此外，混合澄清槽的混合室内两相间时刻发生物质交换过程，虽然物理搅拌减小了载体半径和液膜厚度，但相间传质的扩散过程依然存在传质阻力，物料平衡并不能在Δt时间内完成。若计算模型以稳态时的分配比进行模拟物料交换则会产生误差。

MPMS在模型中考虑了传质阻力，将分配比优化为稳态时物料平衡的分配比与某一数值(该值为分配比系数，在0到1之间)之积，从而模拟传质阻力的效果。此过程大大降低了误差，减小了远离进料单元处的计算误差，从而使得计算结果更加符合原始实验数据。

MPMS使用的向后微分的隐式积分算法对刚性计算体系具有更好的适应性，能够在较短时间内精确地计算刚性较大的常微分方程组，适用于多化学反应体系。

以上，MPMS通过模拟传质阻力得到了比MIXSET-X更优的计算结果，计算结果表明该模型相比于MIXSET-X更为有效。但是应该正视模拟结果存在的误差，这可能是由以下原因共同引起的：

(1) 化学反应的反应速率是经验或半经验公式，与真实的反应速率之间存在差异；

(2) 该模型简化了混合和传质过程，认为混合是完全均匀的，传质只发生在混合室；

(3) 由于计算体系的刚性较大，虽然该隐式积分算法可计算刚性体系，但计算过程中可能仍存在计算误差。

下一步本课题组将针对这三个可能的误差来源对反应速率参数进行修正，并优化混合传质的模型和积分算法，以进一步提高该模型的精确性和可用性。

3 结 论

建立了适用于两端加料和中间加料的混合澄清槽的传质模型，并基于该模型基础上引入分配比模型和化学反应模型，构建了一个适用于模拟以混合澄清槽为分离设备的PUREX流程的物料走向的计算机模型MPMS。PUREX流程中的化学反应涉及到刚性方程组的计算。MPMS使用可解决刚性问题的向后微分的隐式积分算法，可在较短的时间内获得较高的计算精度，较好地解决了其他算法复杂度高、精度低的缺陷，降低了计算的误差。此外，MPMS通过减小分配比系数模拟传质阻力，显著地提升了计算的准确度。通过计算机模拟，MPMS得到了两组应用于不同分液漏斗模型下的计算结果。对比原始实验数据，结果表明该计算模型可以较好地匹配实验值，并展示了比MIXSET-X更高的准确度，证明了该计算模型的可行性。这也表明MPMS是一个可以用于设计、优化和评估基于混合澄清槽的溶剂萃取体系的有效工具，具有实际意义。