神经网络模型模拟旋转填充床的有效传质比表面积
2020-07-13刘丽
刘 丽
吕梁学院,山西 吕梁 033001
有效传质比表面积是设计旋转填充床(RPB)的重要参数,其与操作条件、设备尺寸和物料性质密切相关。在高速旋转填料的作用下,液体持续不断地被撕裂成微小的液滴和液膜,使得有效传质比表面积不断更新,从而促进传质过程。因此,高精度和快速准确地预测旋转填充床的有效传质比表面积显得尤为重要。
Munjal 等[1]通过NaOH 吸收CO2来测量有效传质比表面积。陈海辉等[2-3]研究了多级离心雾化旋转填充床中液体流速和转速对有效传质比表面积的影响。胡孝勇等[4]比较了玻璃珠、拉西环和自制打孔碟片3 种填料的有效传质比表面积,发现最后一种填料的性能最佳。杨平等[5]认为旋转填充床的有效传质比表面积为传统填充床的3~7 倍。焦纬洲等[6]构建了不锈钢多孔波纹板填料和聚丙烯多孔板填料的有效传质比表面积经验关联式。Rajan 等[7]发现相邻反向旋转填料的有效传质比表面积大于同向旋转的。Yang 等[8]测量了不同径向厚度、超重力因子、气体和液体流速下有效传质比表面积。姚远[9]证明有效传质比表面积仅仅是流体力学参数。Luo 等[10]在有效传质比表面积的经验关联式中添加了填料特性的影响。宋一凡等[11]优化了超重力因子、气体和液体流率,得到有效传质比表面积为137 m2/m3。罗会娟[12]测量了空腔区域内的有效传质比表面积。Guo 等[13]指出壳区是主要的传质部分。Chu 等[14]研究发现,两段旋转填充床上部区域的有效传质比面积明显大于下部区域的。Tsai 等[15]发现,旋转填充床中添加静态挡板时有效传质比表面积远大于没有添加时。Luo 等[16]采用4 种结构化的不锈钢丝网填料修正了已有的经验关联式。
目前主要采用Onda 等[17]的关联式计算填充床中有效传质比表面积。但旋转填充床与传统填充床的最大差异为碰撞频率(φ),旋转填充床中的填料和液体在离心力作用下发生剧烈碰撞,使得其碰撞频率远大于传统填充床中的物料。Rajan 等[7]提出的关联式中包含了液体雷诺数(ReL)、液体弗劳德数(FrL)和液体韦伯数(WeL)的影响。Luo 等[10,16]在其关联式中又增加了填料特性参数(ψ)和气体雷诺数(ReG)的影响。
上述有效传质比表面积的关联式是在特定的实验条件下得到的,很难将其拓展应用于其他过程,很大程度上限制了其发展。因此,研究人员尝试采用了多种类型的神经网络(ANN)模型对旋转填充床中的单元操作过程进行模拟[18-22]。本工作将采用前馈反向传播神经网络(FFBP)模型、广义回归神经网络(GR)模型、串并联叠层神经网络(CFBP)模型、径向基神经网络(RB)模型和埃尔曼正向反向神经网络(EFBP)模型模拟旋转填充床的有效传质比表面积(a),并通过实验对模型进行验证,进一步预测超重力因子(β)、气体流量(G)和液体流量(L)对有效传质比表面积的影响。
1 神经网络模型
有效传质比表面积的预测在Matlab(R2015a)软件平台中的神经网络/数据管理器中进行。神经网络模型包含3 个部分:输入层、隐含层和输出层,如图1 所示。
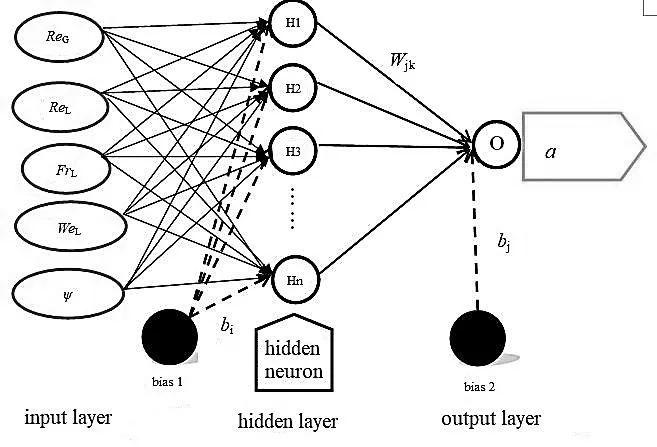
图1 有效传质比表面积的神经网络模型Fig.1 ANN model for effective interfacial area
对实验过程进行深入分析后,选择表征气体流量的参数、表征液体流量的参数、表征转速的参数、表征液体特性的参数和填料特性参数5 个无因次数组作为模型的输入参数,其定义见式(1)~式(5),有效传质比表面积作为模型的输出参数。

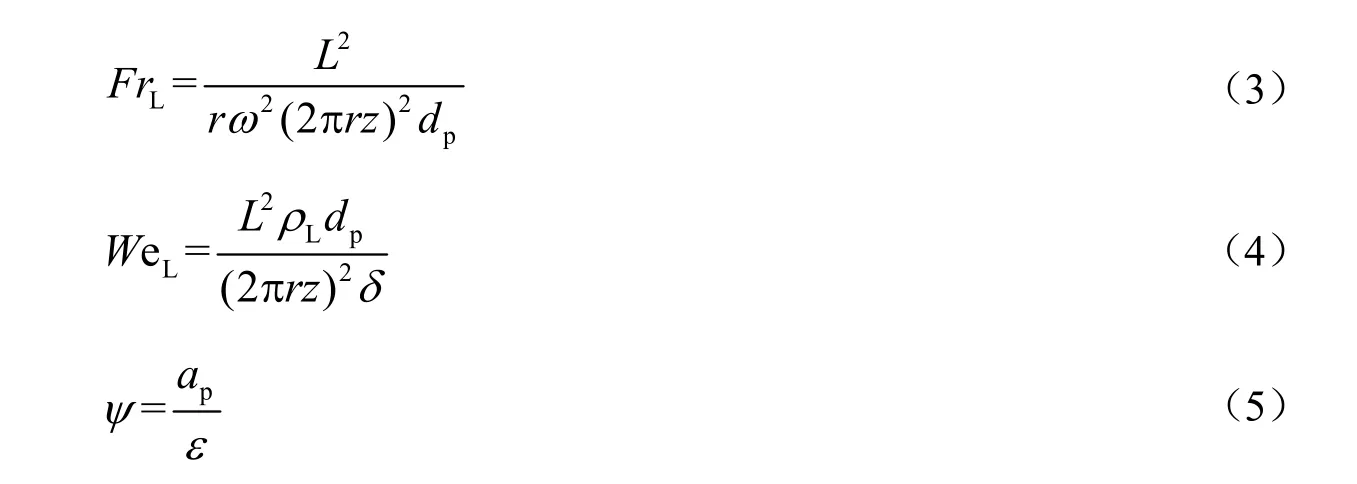
神经网络模型采用的计算数据来自文献[8,10,14-15],实验条件如表1 所示。从表1 可以看出,在不同类型的填料、超重力因子、气体流量和液体流量的条件下,旋转填充床中的有效传质比表面积变化很大(105~750 7 m2/m3)。其中超重力因子采用式(6)进行计算。
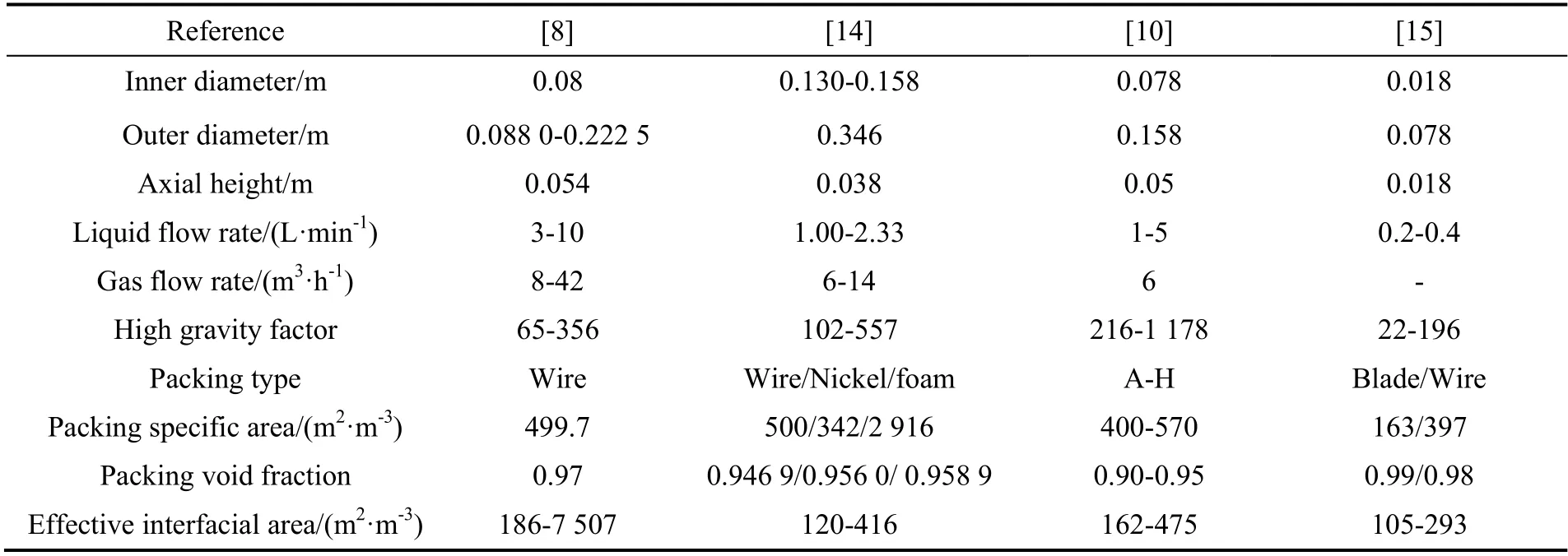
表1 不同旋转填充床有效传质比表面积的实验条件Table 1 The experimental conditions of effective interfacial area for different RPBs
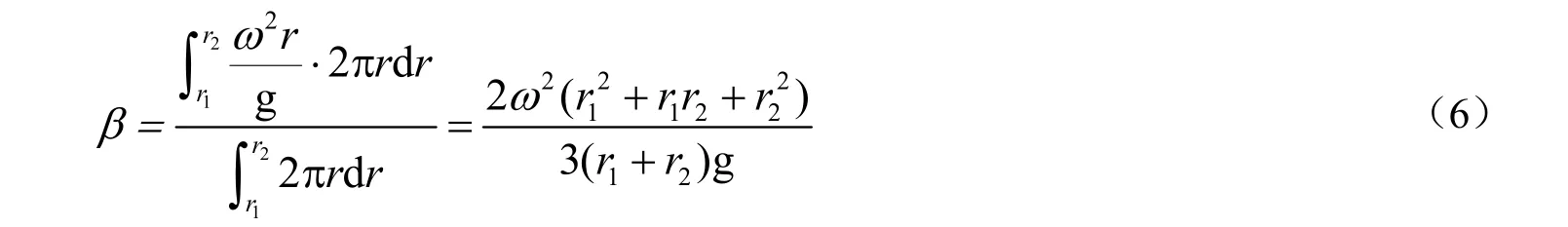
用于计算旋转填充床的有效传质比表面积的5 种神经网络模型,其主要区别在于:FFBP 模型考虑了信息的非直接传递;GR 模型加强了非线性的近似能力;CFBP 模型通过输入和先前的数值进行模型参数的修正;RB 模型采用了高维曲线拟合算法来提高精度;EFBP 模型通过存储信息以及调节前一层的参数来提供时均特性参数。模型的准确性随着隐含神经元数量的增加而增加,但其复杂程度也随之增加。模型采用Levenberge-Marquard 算法和Meta-modeling 算法作为优化算法。Tanh 函数和Sigmoid 函数作为神经元传递函数。为了使模型具有更广泛地的应用和说服力,随机生成模型参数,并对模型进行了验证性检查。根据均方误差(E2)和相关系数(R2)确定神经网络模型的类型和隐含神经元个数。
2 结果与讨论
2.1 不同神经网络模型的比较
不同神经网络模型和隐含神经元数下的有效传质比表面积模拟值(aSim)和实验值(aExp)的比较如图2 所示。由图2 可知,不同神经网络模型的预测值与实验值非常接近,表明神经网络模型可以很好地预测旋转填充床的有效传质比表面积。其E2和R2如表2 所示。

表2 不同神经网络模型的性能Table 2 The performance of different kinds of ANN models
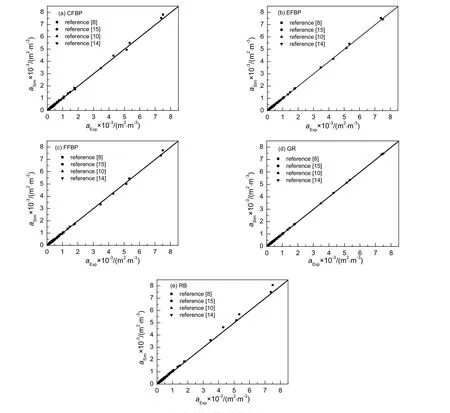
图2 实验值和模拟值的对比Fig.2 Comparison of experimental and simulated results
根据E2和R2结果可知,5 种神经网络模型的预测性能从优到劣依次为GR 模型,EFBP 模型,FFBR模型,CFBP 模型和RB 模型。GR 模型表现良好的性能可能归因Meta-modeling 算法以及加强的非线性近似计算能力。综合考虑E2和R2结果以及隐含神经元的个数,选择GR 模型模拟分析超重力因子、气体流量和液体流量对有效传质比表面积的影响。
2.2 模拟分析
2.2.1 超重力因子对有效传质比表面积的影响
有效传质比表面积越大,其传质速率越高。旋转填充床中最重要的特性是可以通过实时控制超重力因子来控制传质速率。超重力因子对有效传质比表面积的影响如图3 所示。由图3 可知,有效传质比表面积随着超重力因子的增加而增加[8,10,15]。随着超重力因子从21 增加到196[15],模拟的有效传质比表面积从206 m2/m3增加到284 m2/m3。因为随着超重力因子增加,更大的剪切力施加在填料上,从而形成更小的液体传质单元,使得液体更新频率、气液相对速度和碰撞程度增加。此外,液体传质单元厚度减小,使得更多填料被润湿,有助于有效传质比表面积的提高。不同填料之间的有效传质比表面积差异可能是由于填料的直径和开口尺寸不同所致。
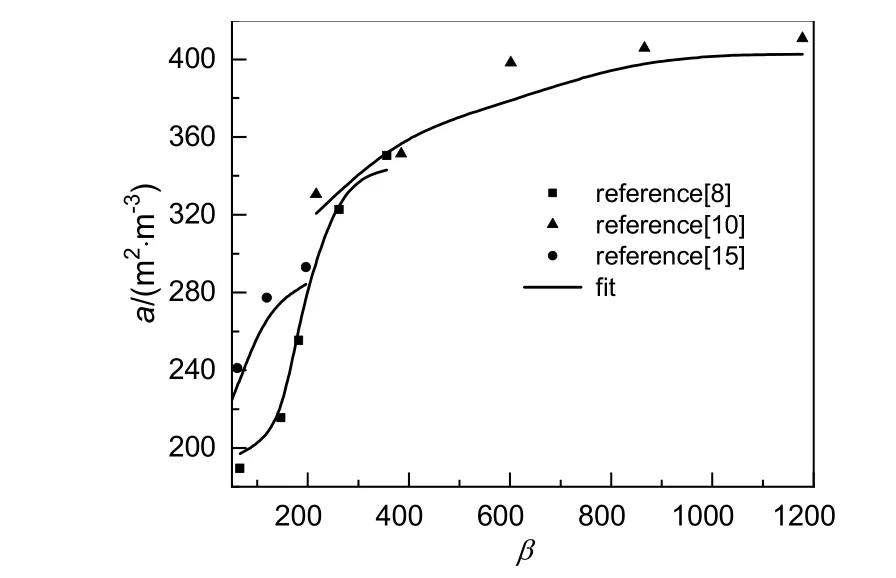
图3 超重力因子对有效传质比表面积的影响Fig.3 Effect of high gravity factor on the effective interfacial area
2.2.2 气体流量对有效传质比表面积的影响
气体流量对有效传质比表面积的影响如图4所示。图4显示,随着气体流量从8 m3/h增加到42 m3/h,模拟的有效传质比表面积从200 m2/m3增加到314 m2/m3,增加了约0.5 倍。这是由于气体流量的增加,气体速度、气液比、湍流程度和液体分散性都随之增加,因此有效传质比表面积增加。

图4 气体流量对有效传质比表面积的影响Fig.4 Effect of gas flow rate on the effective interfacial area
2.2.3 液体流量对有效传质比表面积的影响
液体流量对有效传质比表面积的影响如图5 所示。由图5 可见,对不同的旋转填充床,液体流量对有效传质比表面积的影响程度不同。从3 L/min 增加到8 L/min,模拟的有效传质比表面积从206 m2/m3缓慢增加至281 m2/m3,随后当液体流量再增加时,有效传质比表面积略有下降[8]。相比之下,当液体流量从1 L/min 增加到5 L/min,有效传质比表面积从248 m2/m3迅速增加到480 m2/m3[10]。液体流量较小时,两种情况下的有效传质比表面积都随液体流量的增加而增大,这是因为更多的液体进入到旋转填充床中,形成更小的液体单元,使得更多的填料被润湿;气体和液体之间产生湍流程度增加,使有效传质比表面积增加。但是,随着液体流量的增加,液体停留时间减少,小的液体传质单元之间合并的可能性增加,使得有效传质比表面积下降。当液体流量小于某个临界流量时,有利因素占主导地位,如小的液体传质单元、更多的填料被润湿和气体和液体之间的湍流程度,使得有效传质比表面积随着液体流量的增加而增加;当液体流量大于临界流量时,液体之间的合并占主导地位,使得有效传质比表面积减小。
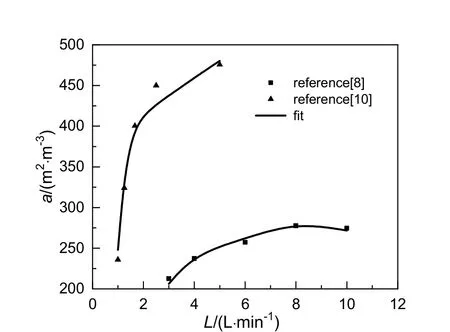
图5 液体流量对有效传质比表面积的影响Fig.5 Effect of liquid flow rate on the effective interfacial area
3 结 论
采用5 种神经网络模型对旋转填充床的有效传质比表面积进行了模拟。考察了气体流量、液体流量、转速、液体性质和填料特性的影响,选择气体雷诺数、液体雷诺数、液体弗洛德数、液体韦伯数和填料特征参数5 个无量纲准数作为模型的输入参数,有效传质比表面积作为模型的输出参数。模型预测结果与文献实验数据的吻合较好,说明神经网络模型可以作为一种快速而精确的方法来估计旋转填充床有效传质比表面积。GR 神经网络模型的模拟预测表明,有效传质比表面积随超重力因子和气体流量的增加而增加,在较低液体流量时,有效传质比表面积随液体流量的增加而增加,超过临界流量后随其增加略有减小。
符号说明
α—— 有效传质比表面积,m2/m3
bj—— 模型参数
dp—— 填料的有效直径,m
FrL—— 液体弗鲁德数
G—— 气体流量,m3/h
L—— 液体流量,L/min
ReG—— 气体雷诺数
ReL—— 液体雷诺数
r—— 填料外径,m
vG—— 气体黏度,Pa·S
vL—— 液体黏度,Pa·S
WeL—— 液体韦伯数
Wjk—— 模型参数
z—— 轴向高度,m
β—— 超重力因子
ψ—— 填料特性参数
ω—— 转速,rad/s
ρL—— 液体密度,kg/m3
δ—— 表面张力,N/m
