具有弹性放大器的双稳态压电俘能器建模及参数影响分析

2020-05-23王建国

计算力学学报 2020年2期

张宇，汪权，王建国

(合肥工业大学土木与水利工程学院，合肥 230009)

1 引言

压电俘能器可以将环境振动转化成电能，为微电子器件自供电提供了一种可行的途径。线性压电俘能器LPH只能在固有频率附近非常有限的带宽内有效，能量转化效率低[1-3]。

为了提高能量俘获的效率，双稳态非线性俘能器越来越受到学者重视[4]。相对于LPH而言，双稳态压电俘能器BPH的输出电压和工作频带都有大幅度改善[5-10]。然而，当外界激励强度较低时，BPH无法产生大幅度阱间运动，仅在单一势阱内产生小幅度阱内运动，因而不能充分发挥BPH的优势，降低了俘能效率。

为了使俘能器在较低的外部激励下获取电能，Aldraihem等[11]提出了带有弹性放大器EM的俘能器，并建立了相应的分析模型。唐礼平等[12]提出了新型弹性放大器，建立了分布参数型运动微分方程，获得了相应的解析解。Wang等[13]研究了具有弹性放大器的双稳态俘能器BPH+EM的非线性动力学特性。弹性放大器的主要功能是放大基底激励的振幅或加速度，使双稳态俘能器在较低基底激励下产生大幅度阱间运动，提高俘能器的工作效率。

本文采用机电耦合的广义Hamilton原理，建立了具有弹性放大器的双稳态压电俘能系统的力学模型，并利用调和平衡法获得了该系统的解析解。研究了弹性放大器刚度质量比对BPH+EM性能的影响，将BPH+EM与BPH的性能进行了分析对比。

2 俘能器的结构模型

图1为BPH+EM结构模型。BPH由悬臂式压电双晶片复合梁和三个永久磁铁组成，梁的左端固定在U型框架的左侧壁，一块磁铁固定在悬臂梁的右端(尖端磁铁)，另两块磁铁固定在U型框架的右侧壁(外部磁铁)，尖端磁铁与外部磁铁间的水平距离为d，两块外部磁铁间的竖向距离为2h，调整磁铁间的距离，可以改变磁力势能的大小。悬臂梁由基层和上下两层厚度相等的压电层组成，每个压电层上下两个表面由薄电极完全覆盖。两个压电层在厚度方向上极化相反，并与外部负载电阻串联电连接。EM包括U框架和弹簧元件，EM位于BPH和基底之间。

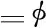
力电耦合的广义Hamilton原理为

(1)

式中δ是变分符号，T为系统动能，UB为压电双晶片复合梁的势能，UM为磁铁相互作用产生的磁力势能，Um为放大器的势能，We为压电片中的电能，W为外力功，分别表示为

(2)

(3)

(4)

(5)

(6)

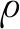
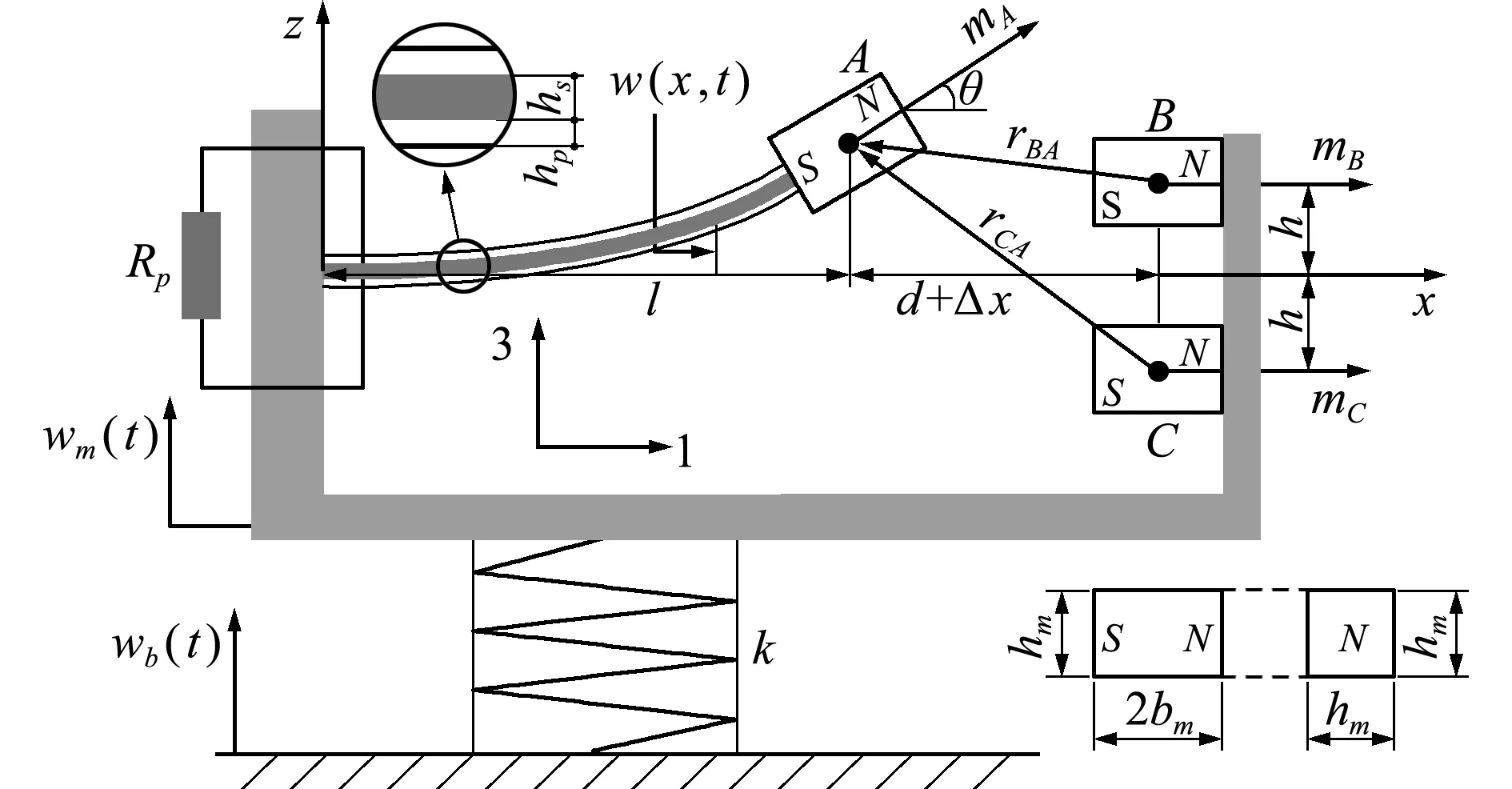
图1 BPH+EM结构模型

Fig.1 Model of bistable piezoelectric energy harvester with elastic magnifier

磁力势能是由A,B和C三块磁铁相互作用产生。利用磁偶极子模型[14]，磁力势能表示为

(7)

式中真空磁导率μ0=4π×10-7H·m-1，mA=[MAVAcosθ，MAVAsinθ]，mB=[MBVB，0]，mC=[MCVC， 0]，MA=MB=MC=M0为磁铁的磁化强度，VA=VB=VC=2bm×hm×hm为磁铁体积。

因bm≪l,θ≈0，则bmsinθ≪w(l,t)，Δx≈0，rB A=[-d，w(l,t)-h]，rC A=[-d，w(l,t)+h]。

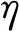
(8)

(9)

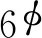
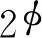
(10)

(4d4-27d2h2+4h4)+

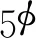
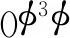
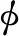
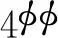
(11)

将方程(2～6,8)代入方程(1)，进行变分运算可得

(12)

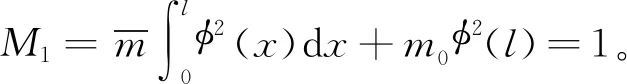
(13)

式中 (·)和(··)分别代表对时间τ的一次和两次导数，其他符号定义如下。

3 调和平衡法

采用调和平衡法，求出BPH+EM系统动力响应的解析解。利用方程(13)第一式与第二式消去变量b，方程(13)简化为

(14)

式中F=-M2Fe/Kl。

假设方程(14)的解可表示为

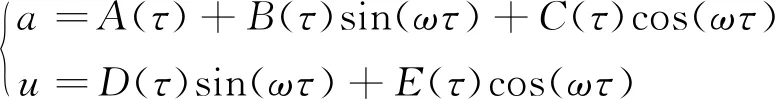
(15)

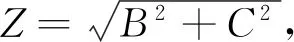
(16)

(17)

(18)

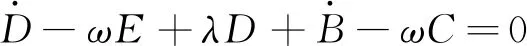
(19)

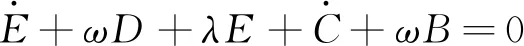
(20)

在方程(16～18)中，

(21)

在稳态情况下，所有对时间的导数均等于0。利用方程(16)可以得到，阱间运动时A=0，阱内运动时A2=-(k1/k2+1.5Z2)。利用方程(17～20)能够求得梁端位移以及电压幅值的解析表达式为

(22)

(23)

方程(22)是变量Z的6次非线性代数方程。由方程(22)求出Z，然后代入方程(23),即可求出V。根据功率与电压的关系，得到功率的表达式为

(24)

4 结果与讨论

利用第3节获得的解析表达式，研究具有弹性放大器的双稳态俘能器BPH+EM的动力性能，讨论弹性放大器的质量刚度比对能量俘获的频带宽度和俘能效率的影响。

当弹性放大器的无量纲刚度km→∞时，方程(14)退化为普通双稳态俘能器BPH的运动方程：

(25)

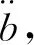
(26)

方程(26)的外部激励为0，故而动力响应为0。因此,可以得到如下推论，当km→0但不等于0时，BPH+EM的俘能效果低于BPH。

分析中采用的物理和几何参数如下[14,15]。

l=71.68 mm,bs p=12.62 mm,hs=0.76 mm

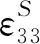
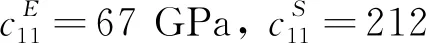
ζ=0.01,e31=-11.6 C/m2,YI=0.2079 N·m2

d=9.5 mm,h=8.5 mm,mm=0.12 kg

k=30 kN/m

取激励强度F=0.001和激励频率ω=1.0，分析BPH+EM与BPH俘能效果的差异。

图2表明BPH的频率响应曲线仅有一个共振峰值，功率峰值P=0.01462 W(ω=1.31);而BPH+EM的频率响应曲线则有两个共振峰值，P1=0.25501 W(ω=1.55)，P2=0.02621 W(ω=1.96)，两个共振峰值之间存在有限的频带宽度。BPH+EM的俘能效率和频带宽度都优于BPH。

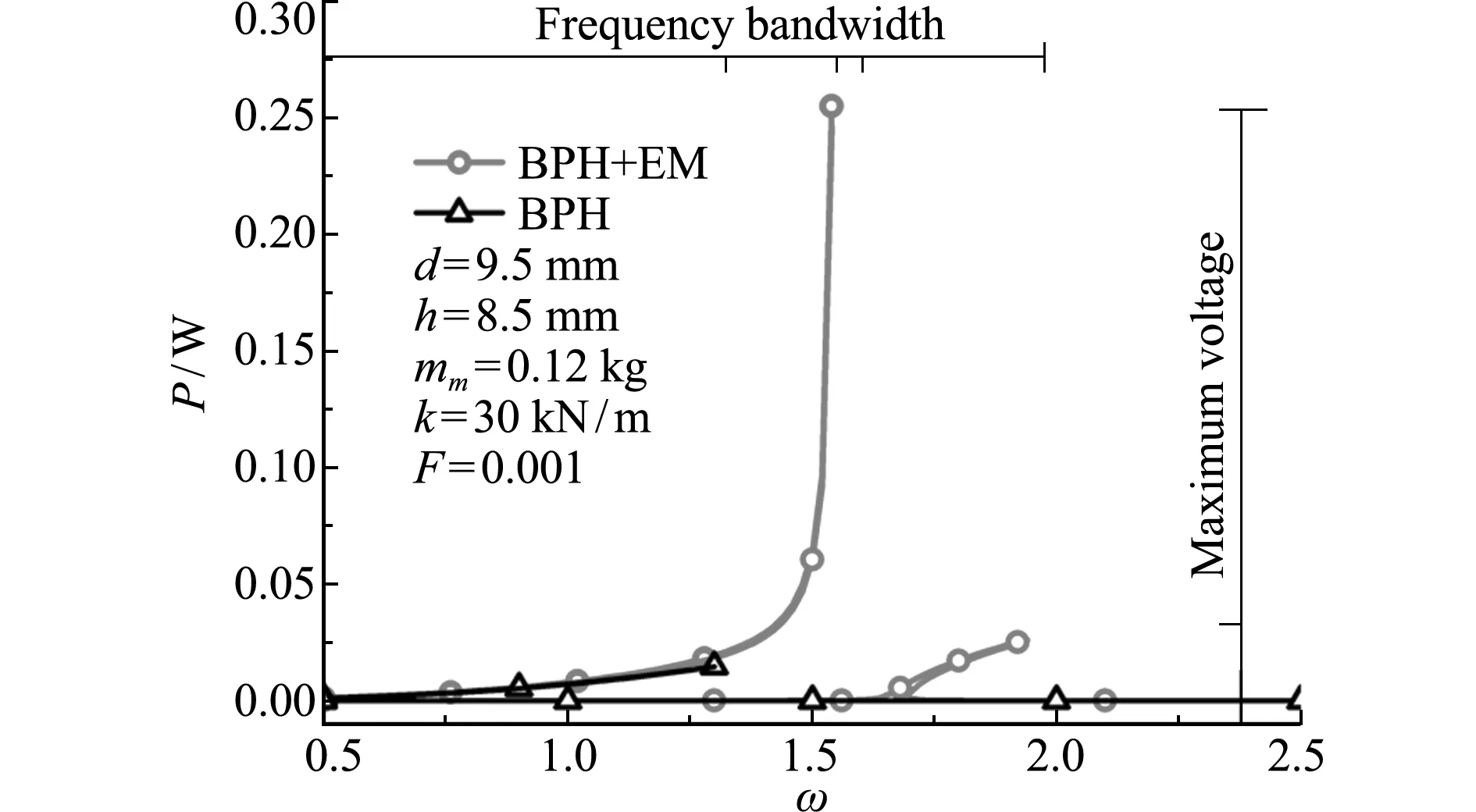
图2 功率-频率响应曲线

Fig.2 Power-frequency response curve

图3表明BPH只有一个功率峰值P= 0.01462 W(ω=1.31)，BPH+EM的第一功率峰值为P1=0.00767 W(ω=0.56)，第二功率峰值为P2=0.00529 W(ω=0.96)。说明在刚度质量比较小时，BPH+EM的功率峰值低于BPH的功率峰值，验证了方程(26)推论的正确性。

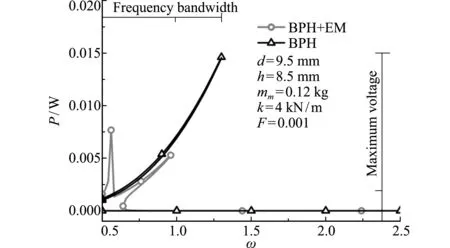
图3 功率-频率响应曲线

Fig.3 Power-frequency response curve

从图4可以看出，BPH+EM在F=0.000378处发生大幅阱间运动，并产生V=0.03223的输出电压，而BPH在F=0.000624时才能产生大幅阱间运动，且输出电压V=0.03106。因此，BPH+EM由阱内运动转换为阱间运动所需要的起始激励阈值低于BPH所需要的起始激励阈值。

图4 电压-激励强度响应曲线

Fig.4 Voltage -excitation response curves

图5表示弹性放大器的刚度质量比rk m=k/mm对BPH+EM系统产生阱间运动所需要的起始激励阈值的影响。随着rk m增加，起始激励阈值快速减小并达到最小值；随着rk m的增加，起始激励阈值缓慢增大并逼近BPH的起始激励阈值。当激励频率ω分别为1.0,1.5和2.0时，最优rk m分别为83.3，250.0和416.7，对应的起始激励阈值分别为0.00011，0.00014和0.00018，因而不同的激励频率所对应的最优rk m是不同的。

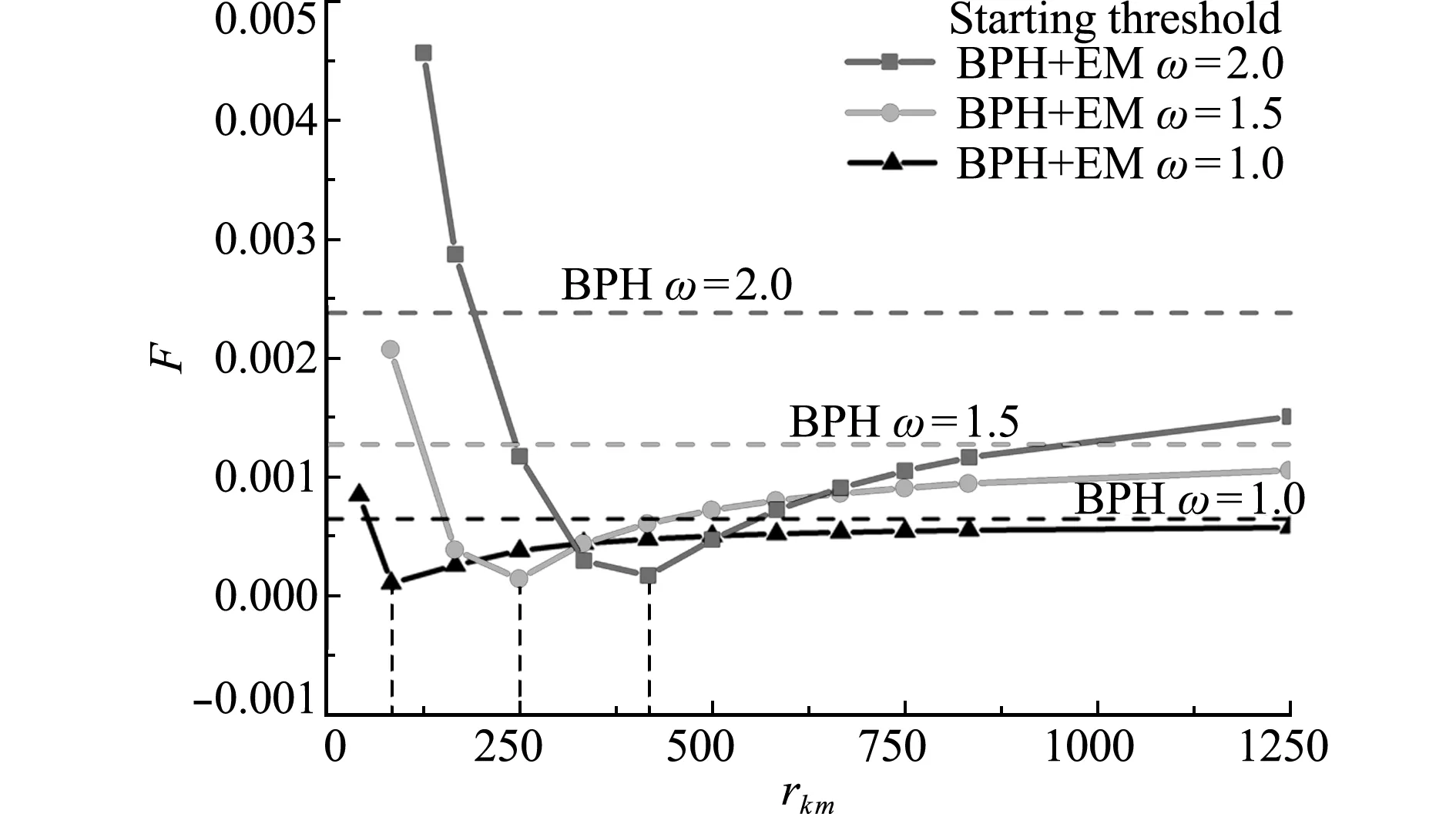
图5rk m对起始阈值的影响

Fig.5 Effect ofrk mon starting threshold

图6表示弹性放大器刚度质量比rk m对功率-频率响应曲线的影响。rk m分别为105.0，235.0，416.7和713.3时,对应的第一功率峰值和频率为P1=0.07146 W(ω=1.00)，P1=0.17989 W(ω=1.50)，P1=0.56204 W(ω=2.00)和P1=0.05412 W(ω=2.00)。

图6 不同rk m时的功率-频率响应曲线

Fig.6 Power-frequency response curve of differentrk m

图7表示随着rk m增大，BPH+EM功率峰值的变化曲线。当激励强度F分别为0.001,0.002和0.003时，功率峰值P的最大值分别为1.20683 W，1.96131 W和3.28103 W，对应的最优rk m分别为625.0，125.0和1875.0。

图7rk m对电压峰值的影响

Fig.7 Effect ofrk mon maximum voltage

图6和图7的结果均表明，随着rk m的增大，BPH+EM的功率峰值增大，rk m达到某一量值时，功率峰值达到最大值；然后，随着rk m的增大，功率峰值逐渐减小，因而弹性放大器存在最优的刚度质量比rk m；随着rk m趋于无限大，BPH+EM功率峰值与BPH功率峰值相同。

图8表示rk m对BPH+EM的频带宽度的影响。激励强度F分别为0.001，0.002和0.003时，最优的rk m分别为625.0，1450.0和2000.0，对应的频带宽度分别为2.62，3.92和4.68。图8表明，在rk m较小时，BPH+EM的频带宽度小于BPH的频带宽度；随着rk m增大，BPH+EM的频带宽度逐步增加并超过BPH的频带宽度，达到极值；然后，随着rk m增大，BPH+EM的频带宽度逐步减小，最终逼近BPH的频带宽度。