求解可压缩流的二维通量分裂格式

胡立军，翟 健，袁 礼

(1.衡阳师范学院 数学与统计学院，衡阳 421002； 2.曙光信息产业(北京)有限公司，北京 100193； 3.中国科学院数学与系统科学研究院 计算数学与科学工程计算研究所，北京 100190)

1 引 言

近几十年，求解可压缩流的Godunov类型黎曼解法器的研究吸引了大量计算流体力学研究人员的关注[1]。中心格式[2]、通量差分裂格式[3]、通量向量分裂格式[4,5]、HLL类格式[6-12]和AUSM-类格式[13]已经广泛地应用于流体力学的数值计算中。这些数值方法都是基于方向分裂的思路来设计的，在计算网格界面数值通量时，只考虑了法向的波系，忽略了横向波系的影响[14]。在求解多维问题时，不仅会降低格式的分辨率，而且稳定性CFL数也会减小，从而影响格式的计算效率[15]。许多研究人员做了大量的研究来克服这些问题，其基本思路是在数值通量的计算中增加横向波的影响，进而设计一种真正多维的数值格式。

一些研究人员尝试对一维黎曼解法器进行复杂的组合来实现多维迎风性。如Rumsey等[16]将多维性引入到一维Roe黎曼解法器中，Colella[17]提出的多维角点输运格式和LeVeque[18]设计的多维波传播算法。尽管这样处理可以增加稳定性CFL数，但是常会以求解大量的一维黎曼问题作为代价。另外一些研究人员尝试去建立更加复杂的多维波传播模型，从而获得一种线性化的多维Roe格式[15,19]。但是该解法器只能用来计算欧拉方程，很难推广到其他的守恒律系统。此外，Wendroff[20]利用HLLE格式适用于任何守恒律系统这一特性来构造一种多维的HLLE格式，但是该格式引入了九个常数状态，形式非常复杂。

Balsara[21]基于一维HLLE格式构造了一种简单高效的真正二维黎曼解法器。与其他多维格式不同，该格式具有简单的封闭形式，其算法很容易实现。为了克服二维HLLE格式无法捕捉接触间断和剪切波的缺陷，引入一个子波系，在HLLC格式的基础上对二维HLLE格式进行了改进。文献[22]的结果表明，真正二维的HLLC格式能够精确分辨接触间断。Balsara等[23]对具有自相似内部结构的多维黎曼问题提出了一种求解策略，并且构造了一种可以用来求解守恒律和非守恒律问题的多维HLLI格式，该格式在数值计算中不需要详细区分接触间断的方向。

采用Balsara的思路，Mandal等[24]利用HLL-CPS格式的优点并且结合Zha-Bilgen分裂方法，构造了一种真正二维的HLL格式。胡立军等[14]基于 Toro -Vázquez 分裂方法，在二维结构网格上构造了一种真正二维的HLL黎曼解法器。Qu等[25]将该黎曼解法器推广到了二维曲线坐标系。结合通量分裂方法设计的多维黎曼解法器，形式简单并且计算代价小，为构造真正多维黎曼解法器提供了一条新的思路。

本文以传统的一维TV格式[26]为基础，构造一种简单的真正二维TV通量分裂格式。

2 Toro -Vázquez 分裂方法

2.1 控制方程组

直角坐标系下的二维欧拉方程组为

(1)

式中

(2)

ρ为密度，u和v为x方向和y方向的流体速度，p为压力，E为总能。状态方程为

(3)

本文比热比γ=1.4。

用守恒型数值方法求解式(1)，

(4)

式中Fi + 1/2,j和Gi,j + 1/2为x和y方向的数值通量。

2.2 对流/压力通量分裂

Toro等[26]将欧拉方程的能量方程分裂成动能项和压力项，从而将通量分裂成对流通量和压力通量。以x方向为例：

F(U)=Ax(U)+Px(U)=

(5)

式中 内能e=p/[(γ-1)ρ]。

对流通量Ax(U)的Jacobian矩阵为

(6)

矩阵B的特征值为

(7)

压力通量Px(U)的Jacobian矩阵为

(8)

矩阵M的特征值为

(9)

3 二维TV通量分裂格式

3.1 界面中点一维通量的计算

根据对流/压力通量分裂式(5)，中点处的一维通量可以分裂成两部分之和。

(10)

3.1.1 中点对流数值通量

使用TV格式[26]来计算网格界面中点处的对流数值通量。以x方向为例

(11)

式中 界面速度

(12)

3.1.2 中点压力数值通量

同样使用TV格式[26]来计算中点处的压力数值通量。将状态方程p=(γ-1)ρe代入压力通量表达式(5)，可以得到压力通量的计算公式为

(13)

界面速度u*的定义见式(12)，界面压力p*的计算公式为

(15)

3.2 界面角点二维通量的计算

根据分裂式(5)，角点处的二维通量可以分裂成两部分之和，即

(16)

3.2.1 角点对流数值通量

使用迎风格式来求解角点处的对流数值通量。通过考虑角点处横向波对数值通量的影响，来实现格式真正二维的特性。其具体的计算公式为

(17)

图1 结构化网格和角点处黎曼问题的四个初态

Fig.1 Structured grid and four initial states at the corner

(18)

迎风方向k1和k2按如下方式来选取。

(19)

3.2.2 角点压力数值通量

为了更好地保留一维TV格式的优点，与文献[14,25]中基于 Toro -Vázquez 分裂方法构造二维HLL格式不同的是，本文压力数值通量使用TV格式而不是HLL格式来求解：

(20)

式中 右端第一项为考虑了影响域面积加权的TV通量，其计算公式为

(21)

(22)

式(20)右端第二项为横向压力通量对角点数值通量的贡献。其中，Py为y方向的压力通量，定义为

(23)

如图1(b)所示，波速SU,SD,SL和SR分别代表沿着上下左右四个方向传播的最快波速，本文按照文献[14]的定义来计算。

3.3 界面数值通量

(24)

4 数值结果

使用本文构造的二维TV通量分裂格式求解几个典型的数值算例来验证格式的精度、鲁棒性和计算效率。

4.1 二维黎曼问题

计算文献[27]的二维黎曼问题来比较三种数值格式，即本文构造的GT-TV格式、一维TV格式[26]和真正二维的GM-TV-HLL格式[14]。计算区域[0,1]×[0,1]划分成400×400的矩形网格，初始条件为

(25)

该算例没有精确解，本文采用HLLC格式在800×800的密网格下所得到的计算结果作为参考解，三种格式的数值解均采用400×400的粗网格来计算。图2展示了计算时间T=0.25时，参考解和三种数值解的密度轮廓。为了更加精细地比较三种数值格式之间的差异，计算数值解与参考解之间的误差，其表达式为

(26)

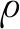
在计算数值通量时，真正二维的数值格式不仅考虑界面法向波系的影响，还考虑了界面横向波系的影响，因此比传统的一维数值格式具有更高的分辨率[15,17]。而GM-TV-HLL格式的压力通量采用耗散较大的HLL格式来计算，从而会带来更大的数值误差。本节数值试验的结果也证明了这 一点。

图2 二维黎曼问题的计算结果

Fig.2 Solutions of two -dimensional Riemann problem

4.2 随机扰动问题

进行数值模拟时，由于各种原因，在初始分布和计算过程中会引入很小的随机扰动。在计算中，随机扰动的发展过程，常用来检验数值格式的鲁棒性。马赫数为10的平面激波从左向右移动，初始物理量上增加10-10倍随机扰动。激波右侧具体的初始分布为

(27)

式中αk(k=1,2,3,4)是(0,1)之间的随机数，计算中由相应的库函数生成。计算区域[0,35]×[0,1]划分成700×20的矩形网格。

图3展示了在计算时间T=3时，使用TV格式和GT-TV格式求解随机扰动问题所得到的计算结果。可以看出，真正二维的GT-TV格式不仅能够精确地捕捉激波的位置(x=30)，而且消除了一维TV格式的波后不稳定现象。在计算中，一维TV格式的稳定性CFL数不能超过0.4，而GT-TV格式的稳定性CFL数最大可以取到0.95。

表1 不同数值格式的误差比较

Tab.1 Comparison of errors between different numerical schemes

SchemeError‖L2(ρ)‖TV4.8325e-5GM-TV-HLL6.3139e-5GT-TV4.0652e-5

图3 随机扰动问题的计算结果

Fig.3 Solutions of random perturbation problem

4.3 后台阶激波衍射问题

后台阶激波衍射问题对于数值格式的鲁棒性要求很高，许多数值格式在计算该算例时都会失效。因此，文献多使用该算例来测试格式的鲁棒性。马赫数为5.09的右行超声速气流绕过90°的角，计算区域[0,1]×[0,1]划分成400×400的矩形网格，角点位置(x,y)=(0.05,0.625)。激波右侧的初始条件为

(28)

图4展示了计算时间T=0.15时，一维TV格式和二维GT-TV格式的计算结果。二维GT-TV格式消除了一维TV格式在区域上边界正激波处的不稳定现象。在计算中，一维 TV格式的稳定性CFL数不能超过0.4，二维GT-TV格式的稳定性CFL数最大可以取到0.9。

文献[11,12]指出，能够精确分辨接触间断的数值格式都会遭受不同程度的激波不稳定现象，并且横向扰动的增长未能得到有效的抑制是造成激波不稳定的根本原因。真正二维的GT-TV格式的数值通量考虑了横向波系的影响，因此横向的数值粘性可以有效地抑制横向扰动的增长，从而消除一维TV格式的激波不稳定性。4.2节和4.3节的数值试验也证明了这一结论。

图4 激波衍射问题的计算结果

Fig.4 Solutions of shock diffraction problem

4.4 计算效率的比较

比较一维TV格式和二维GT-TV格式的计算效率。表2展示了用两种格式计算本文三个数值算例的CPU时间和CFL数取格式允许的最大值。如计算二维黎曼问题时，TV格式的CFL数取0.5，GT-TV格式取0.95。在计算中，GT-TV格式不仅要计算界面中点的数值通量，还需要计算界面角点的数值通量，因此单个时间步的计算量会大于TV格式。但是GT-TV格式可以提高稳定性CFL数[17]，从而增加时间步长，减少CPU计算时间。从表2可以看到，相比于一维TV格式，GT-TV格式的计算效率分别提高了 25.20%，38.62%和36.88%。因此，GT-TV格式具有更高的计算效率。

表2 数值格式计算效率的比较

Tab.2 Comparisons of computational efficiency for numerical schemes

Example1Example2Example3SchemeTime/CFLTime/CFLTime/CFLTV86.58/0.552.17/0.492.64/0.4GT-TV64.76/0.9532.02/0.9558.47/0.9

5 结 论

一维TV通量分裂格式不仅形式简单,而且可以精确捕捉一维激波和膨胀激波。但是,在求解界面数值通量时，只考虑了界面法向的波系，忽视了横向波系的影响。因此,使用一维TV格式求解二维问题时，不仅会减小稳定性CFL数，而且无法保证格式的鲁棒性。本文基于一维TV格式构造的二维TV通量分裂格式,通过求解考虑了横向波系影响的角点数值通量,来克服一维TV格式的缺点。数值结果表明，与一维TV格式相比，本文构造的二维TV格式不仅有更高的分辨率和计算效率，而且有更好的鲁棒性。构造非结构网格上的二维TV通量分裂格式并且将其应用到其他的守恒律系统,可以作为未来的研究工作。