车-轨-桥耦合动力系统影响参数分析
2020-05-23李锦华黎文武管海平李春祥
李锦华,黎文武,管海平,李春祥
(1.华东交通大学 土木建筑学院,南昌 330013; 2.南昌铁路天河建设有限公司,南昌 330026;3.上海大学 土木工程系,上海 200444)
1 引 言

随着我国铁路的不断发展,许多研究者从不同的角度和多种实际因素来分析研究复杂的车-轨-桥耦合系统的动力响应[8-12]。Lin等[13]提出了一种基于2.5D有限/无限单元法的地下隧道地震分析方法。余志武等[14]基于车-桥竖向耦合模型,考虑车辆荷载及一系、二系竖向弹簧刚度与弹簧阻尼的随机性,数值分析了车桥竖向随机振动。张骞等[15]将轨道不平顺作为系统的内部激励,采用自编程序TYWTB建立车桥耦合系统动力学模型,进行了不同风速激励下,不同速度列车通过桥梁时的系统动力响应分析。乔宏等[16]基于子结构方法,将完整的列车-桥梁-桩基础-地基相互作用模型分解为列车-桥梁相互作用子系统和桩基础-地基相互作用子系统,分别建立了两个子系统的运动方程,研究了桩-土动力相互作用对车桥耦合系统动力响应的影响。张鸣祥等[17]在高速铁路桥梁的振动控制方面,通过调谐质量阻尼器来减缓结构承受的巨大冲击。
目前,对于车-轨-桥模型的建立已经较为全面,且列车考虑的角度也更加接近实际,但鲜有学者注意到列车上桥之前的运动状态以及多线列车同时上桥时对耦合系统的动力响应。本文依据高速列车、板式无砟轨道和桥梁相互作用的特点,通过建立该系统的耦合运动方程,重点分析双线列车以不同工况通过高速铁路桥梁时,列车行驶状态(速度和加速度)、列车的悬挂系数和钢轨-轨道-桥梁之间连接参数分别对车-轨-桥耦合系统动力学性能的影响。
2 车-轨-桥系统耦合振动方程
列车-板式无砟轨道-桥梁耦合系统可分为车辆子系统、轨道子系统和桥梁子系统,分别通过轮轨接触关系和桥轨接触关系建立耦合系统的振动方程。列车-板式无砟轨道-桥梁耦合振动模型如图1所示,列车运行的加速度和速度分别为a和v。
2.1 列车子系统
列车子系统模型为10自由度质量-弹簧-阻尼多刚体系。车厢的车体自由度为其质心处的竖向位移uc和转角θc;一系悬挂结构(车体和转向架之间)的弹簧刚度和阻尼系数分别为kc t和cc t;车厢的两个转向架自由度分别为其质心处的竖向位移ut 1和转角θt 1及竖向位移ut 2和转角θt 2;二系悬挂结构(转向架和轮对之间)的弹簧刚度和阻尼系数分别为kt w和ct w;四个轮对自由度为其质心处的竖向位移uw 1,uw 2,uw 3和uw 4。所以每节车厢车体的10自由度分别为
uv=[ucθcut 1θt 1ut 2θt 2uw 1uw 2uw 3uw 4]T
(1)
根据达朗贝尔原理,可建立列车运动方程
(2)

2.2 轨道子系统和桥梁子系统
钢轨、轨道板和桥梁的节点有竖向位移和转角两个自由度。钢轨与轨道板间离散弹性系数和粘滞阻尼系数分别为kd和cd,轨道板与桥梁间连续弹性系数和粘滞阻尼系数分别为kc和cc。
以钢轨欧拉伯努利梁单元为例(轨道板与桥梁欧拉伯努利梁单元类似),得到钢轨欧拉伯努利梁单元的振动方程为
(3)

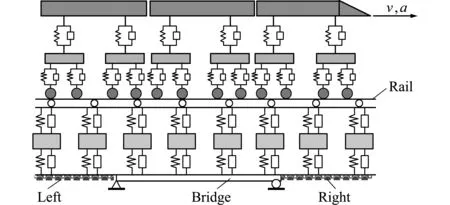
图1 列车-板式无砟轨道-桥梁耦合系统计算模型
Fig.1 Calculation model of train-slab ballastless track-bridge coupling system
ur(x,t)=[N]{ur}e
(4)
[N]=[N1N2N3N4]
(5)
式中 {ur}e表示梁单元节点位移列向量,{ur}e={yn,θn,yn + 1,θn +1}T,其中yn表示n节点竖向位移,θn表示n节点的转角;N表示梁单元形函数,N1=1-3(x/l)2+2(x/l)2,N2=x-2x2/l+x3/l2,N3=3(x/l)2-2(x/l)3,N4=-x2/l+x3/l2,其中x表示从梁单元左节点处开始测量的局部坐标,l表示梁单元长度。
同理,可分别建立轨道板与桥梁的欧拉伯努利梁的振动方程,离散化后,可建立轨道子系统和桥梁子系统的整体运动方程为
(6)

2.3 列车车轮与钢轨接触关系
假定列车车厢每个车轮都与钢轨始终接触,则列车与钢轨之间两点接触的约束方程可写成
uw n(t)=[ur(x,t)]|x = xn=[N]x = xn{ur}e
(7)
(8)
(9)
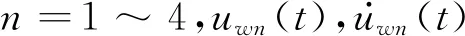
综上所述,列车-轨道-桥梁系统的耦合振动方程可建立为
(10)
3 耦合系统的影响参数分析
首先,需要验证本文耦合系统计算程序的有效性,为此对文献[12]的车桥耦合系统算例进行了数值计算。桥梁的单位质量为2303 kg/m,弹性模量为2.87×109N·m2,惯性矩为2.90 m4,跨径为 25 m;车辆采用弹簧-质量模型,质量块的质量为5750 kg,弹簧刚度系数为1595 kN/m,移动速度为100 km/h。对本文运用的有限元方法进行编程,计算了移动车辆作用下车桥耦合系统的动态响应,如图2所示。可以看出,本文数值计算结果与文献[12]计算结果吻合,从而验证了本文计算方法与程序的正确性。

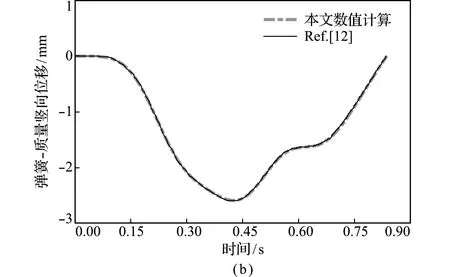
图2 桥梁跨中和弹簧-质量动态响应对比
Fig.2 Comparisons of dynamic response of bridge mid-span and spring -mass
然后,针对耦合系统的影响参数,重点分析列车行驶状态(速度与加速度)、列车的悬挂系统(刚度与阻尼)以及钢轨-轨道板-桥梁的连接刚度和阻尼等分别对列车、轨道和桥梁动力响应的影响。
考虑高速列车为10自由度车辆模型,列车定距之半为8.5 m,转向架轴距之半为1.5 m,双线列车的第一节车厢距离梁桥左端距离均为 10 m,每节车厢之间的间距均为1 m。高速列车车体质量和点头惯量分别为4.2×104kg和2×106kg·m2,高速列车构架质量和点头惯量分别为3×103kg和 4×103kg·m2,高速列车轮对质量均为2×103kg。列车行驶状态(速度与加速度)和列车的悬挂系统(刚度与阻尼)的分析参数列入表1。
表1 列车行驶状态(速度与加速度)和列车的悬挂系统(刚度与阻尼)的分析参数
Tab.1 Analysis parameters of train running state (speed and acceleration) and suspension system (stiffness and damping)

速度/m·s-1加速度/m·s-2刚度/N·m-1阻尼/N·s·m-1一系二系一系二系5025×1051×1069×1044×1046056×1052×1061055×10470107×1053×1061.1×1056×104
钢轨-轨道板-桥梁结构参数如下。简支梁桥跨度为32 m,各阶阻尼比为0.05;钢轨、轨道板和桥梁的弹性模量分别为2×1011N/m2,2×1010N/m2和3×1011N/m2,单位长度质量分别为102kg/m,103kg/m 和9×103kg/m,截面惯性矩分别为4×10-5m4,10-10m4和2.88 m4。不考虑轨道不平顺,钢轨与轨道板的离散连接点间距为0.6 m,轨道板与桥梁的连接为连续支承,钢轨-轨道板-桥梁的连接刚度和阻尼列入表2。
表2 钢轨-轨道板-桥梁的连接刚度和阻尼
Tab.2 Stiffness and damping of rail-slab -bridge connection

钢轨与轨道板的离散连接轨道板与桥梁的连续连接刚度/N·m-1阻尼/N·s·m-1刚度/N·m-1阻尼/N·s·m-110133×1041.5×1096.5×1042×10134×1042.5×1097.5×1043×10135×1043.5×1098.5×104
桥跨位置处的钢轨和轨道板都划分为16个有限元单元,简支梁桥也划分为16个有限元单元,所有单元长度均为2 m。对于建立的列车-轨道-桥梁系统的耦合振动方程,采用Newmark-β平均常加速度积分法对其进行数值求解,耦合系统的影响参数分析如下。
3.1 列车运行状态(速度与加速度)的影响
列车单线三节车厢运行时,分别改变其行驶速度与加速度参数,整个耦合系统结构的位移振动响应结果列入表3。

表3 单线三车厢列车行驶参数改变对耦合系统位移响应的影响(第一节车厢)Tab.3 Influence of the change of train driving parameters on the displacement response of the coupled system in the single -line three -car compartment (the first car)
当列车加速度分别以2 m/s2,5 m/s2和10 m/s2运行时,第一节车厢的车体垂向位移振幅最大百分比为25%,而车体绕质心点头位移振幅的变化在12.71%~16.69%范围内;对于桥梁结构系统,跨中位置处桥梁与钢轨垂向位移振幅变化百分比最大分别达24%和19.23%。
当列车分别以速度50 m/s,60 m/s和70 m/s前行时,第一节车厢的车体垂向位移振幅变化范围为4.08%~10.20%,而车体绕质心点头位移振幅的变化最大达23.18%,跨中位置处桥梁与钢轨垂向位移振幅的变化范围分别为7.69%~15.38% 和7.58%~15.15%。通过表中百分比的正负号代表的意义可知,随着列车速度与加速度在一定范围内的增加,车体自身结构的位移振动响应在逐渐减小,而钢轨和桥梁结构的位移振动响应则在不断增加。
列车行驶加速度和速度对列车车体振动的影响如图3所示。图3(a~c)为列车行驶加速度的影响,当列车分别以2 m/s2,5 m/s2和10 m/s2的加速度行驶过桥时,车体的振动加速度幅值会有所不同,但幅值并无较大改变;前后两节车厢振动加速度明显不同,后一节车体的振动加速度明显小于前一节车体。图3(d~f)为列车行驶速度的影响,当列车分别以50 m/s,60 m/s和70 m/s恒定低速行驶过桥时,车体振动加速度具有类似的变化情况,这说明在一定范围内改变列车行驶速度与加速度对于车体振动加速度的影响是有限的。
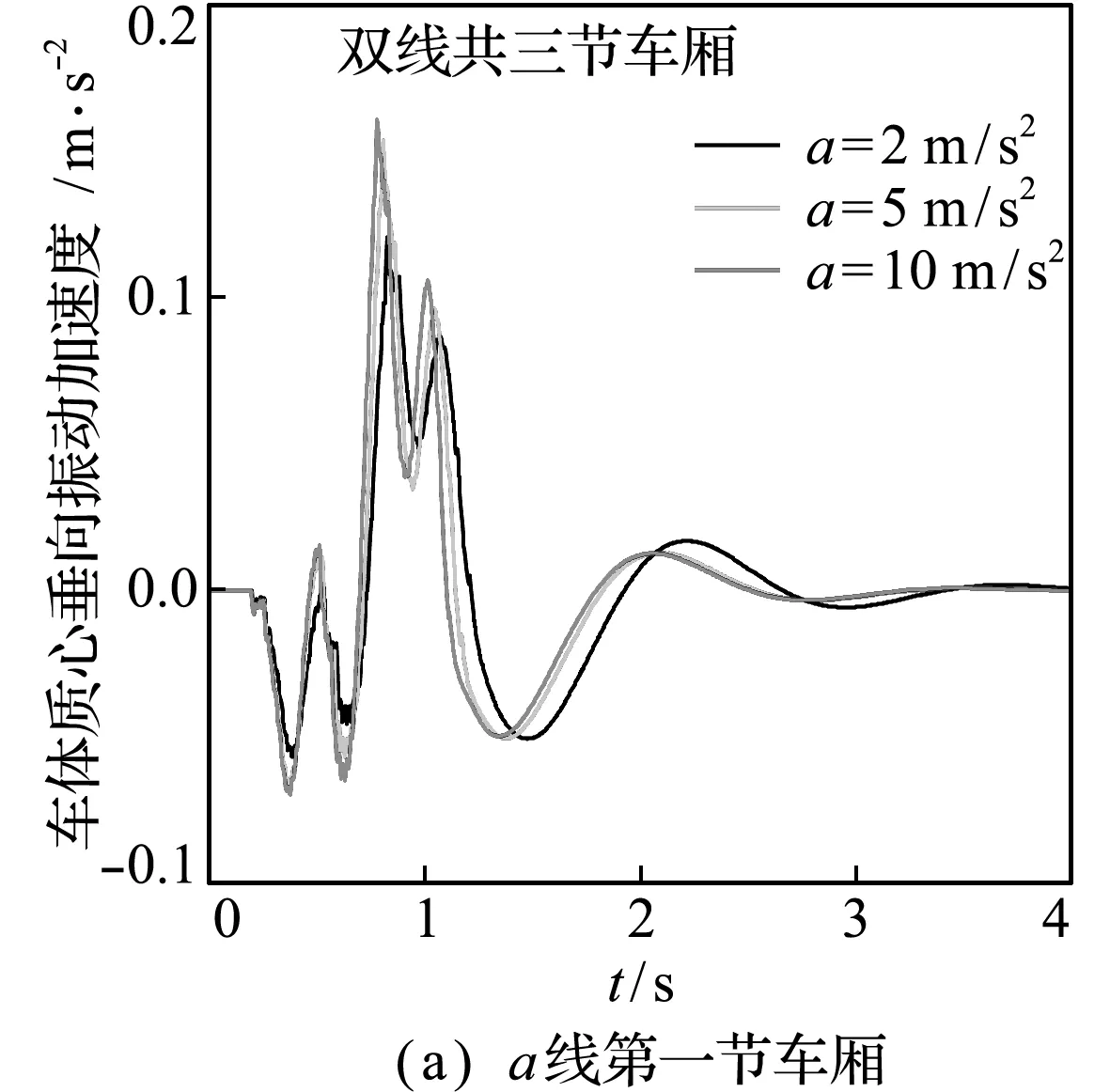
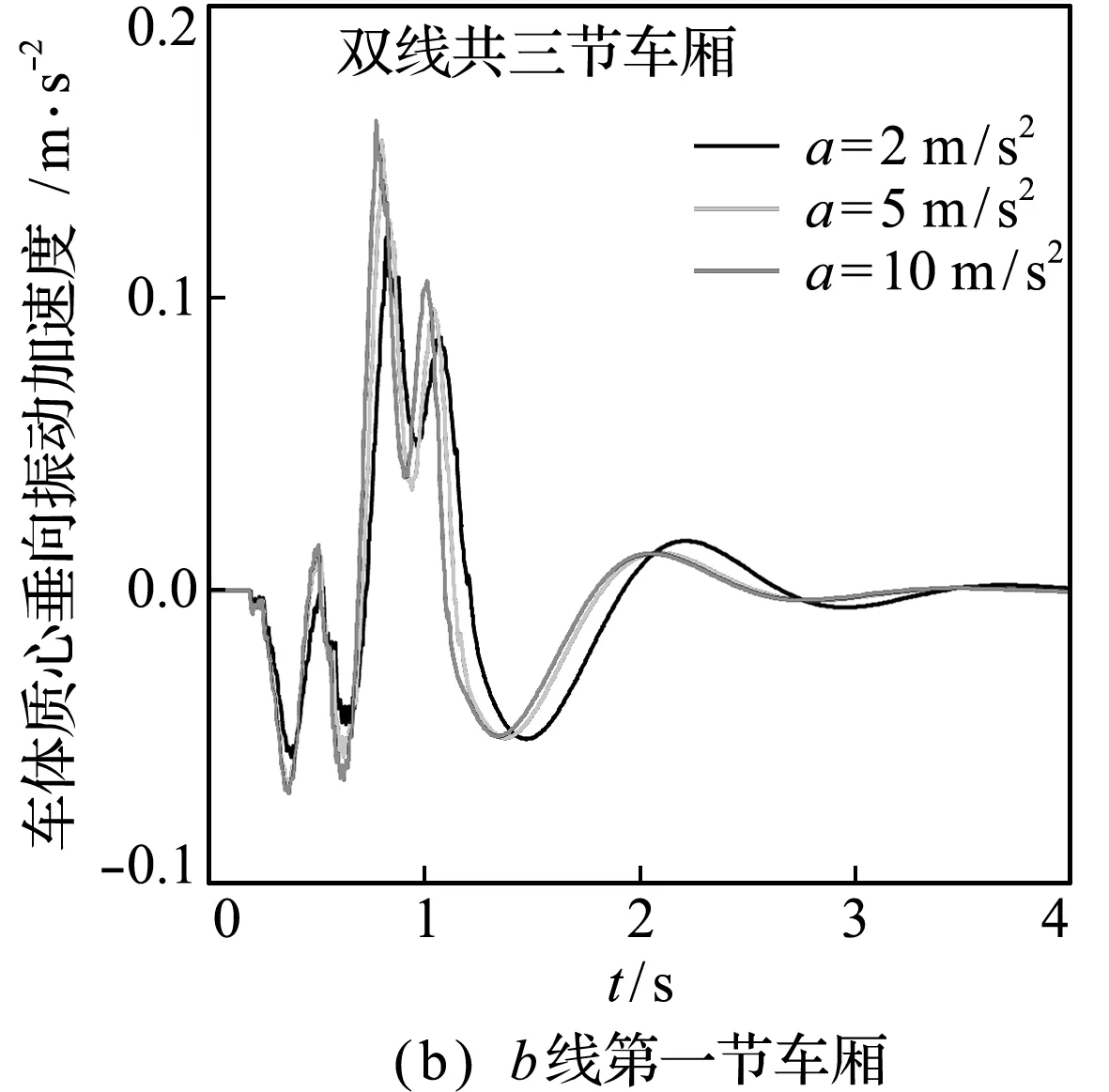
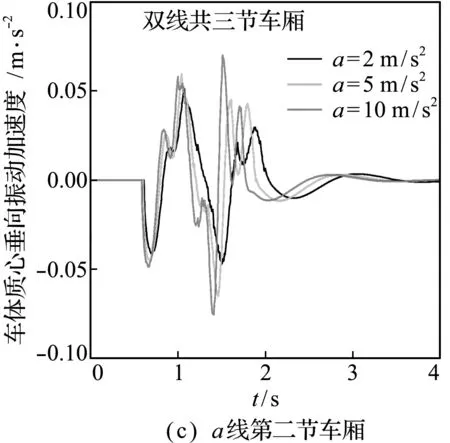
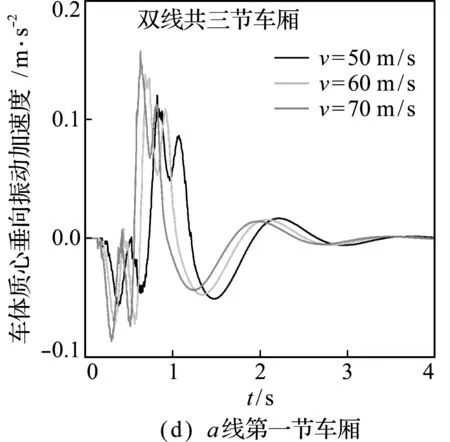
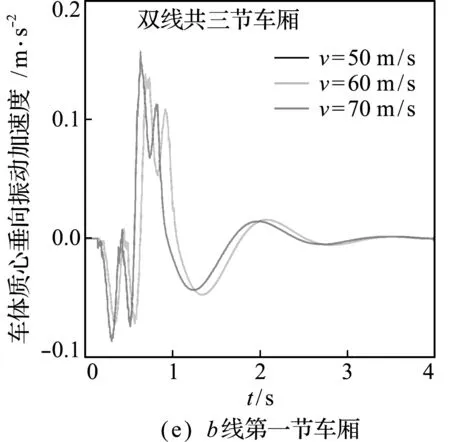
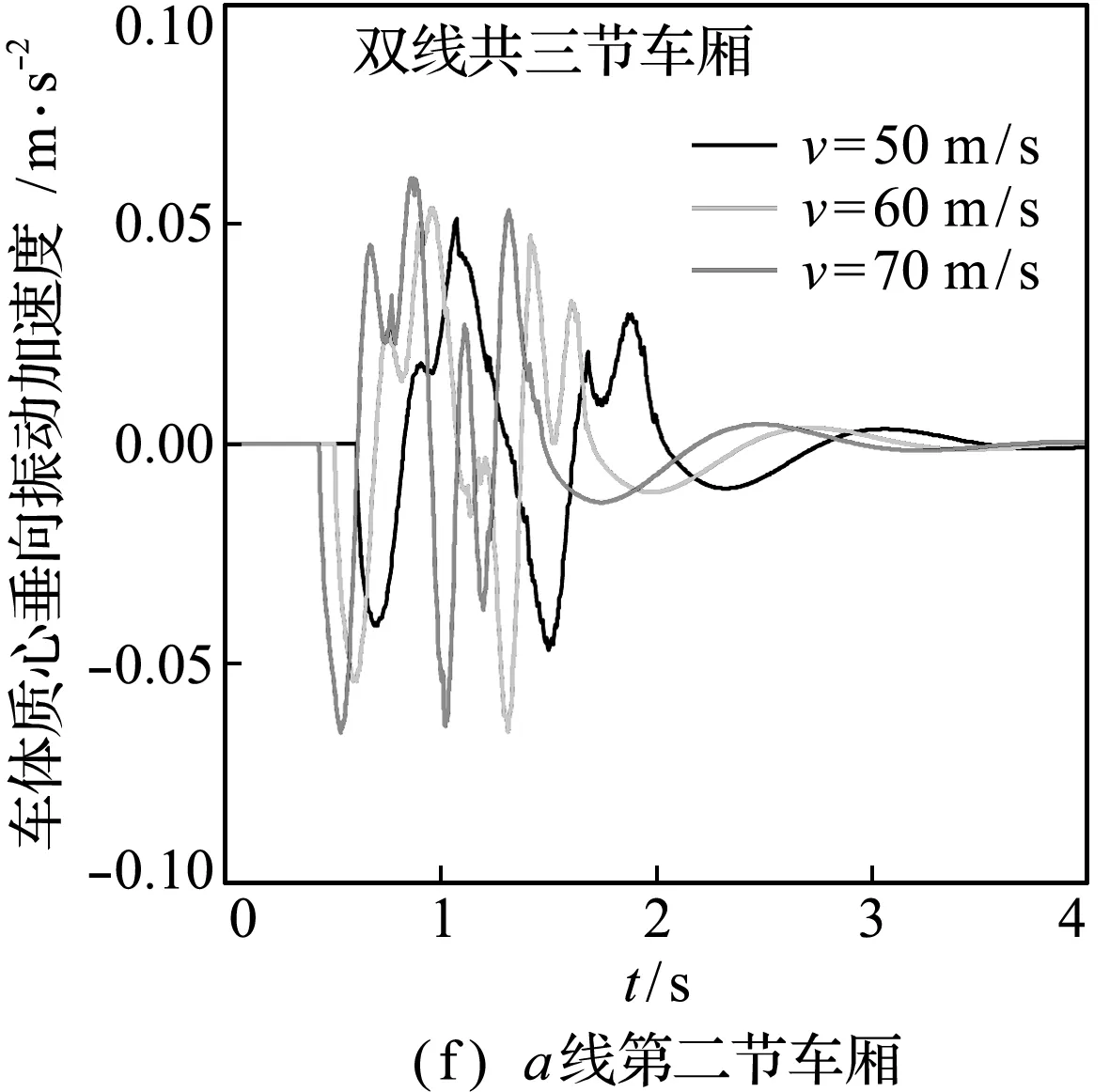
图3 加速度和速度改变时列车车体结构的振动响应
Fig.3 Vibration response of train body structure when acceleration and speed change
3.2 列车悬挂系统(刚度和阻尼)的影响
列车单线三节车厢运行时,改变车体一系和二系刚度系数,整个耦合系统结构的位移振动响应结果列入表4。
当车体一系刚度系数分别为5×105N/m,6×105N/m和7×105N/m时,第一节车厢的车体垂向位移振幅变化在3.85%~7.69%范围内,而车体绕质心点头位移振幅的变化范围为7.48%~14.19%,对于轨桥结构系统,跨中桥梁与钢轨垂向位移均无影响。
当车体二系刚度系数分别为1×106N/m,2×106N/m和3×106N/m时,第一节车厢的车体垂向位移振幅变化范围为18.48%~25.04%,而车体绕质心点头位移振幅的变化最大仅为 8.68%,跨中桥梁与钢轨垂向位移振幅的变化最大也仅为 2.78%。由百分比的正负号代表的意义可知,随着车体一系刚度系数的增加,车体自身结构的振动响应也在不断增加,但车体二系刚度系数的增加却抑制了车体结构的振动响应。
改变车体一系和二系阻尼系数,整个耦合系统结构的位移振动响应结果列入表5。当车体一系阻尼系数分别为9×104N·s/m,1×105N·s/m和1.1×105N·s/m时,第一节车厢的车体垂向位移振幅变化在10.61%~17.35%范围内,而车体绕质心点头位移振幅的变化范围为11.09%~ 20.95%,对于轨桥结构系统,跨中桥梁与钢轨垂向位移均无影响。
当车体二系阻尼系数分别为4×104N·s/m,5×104N·s/m和6×104N·s/m时,第一节车厢的车体垂向位移变化百分比最大仅为3.85%,而车体绕质心点头位移振幅的变化最大仅为 2.70%,跨中桥梁与钢轨垂向位移振幅的变化最大也仅为 2.78%。分析表明,列车一系阻尼系数的改变能够影响车体自身位移振动响应,而列车二系的阻尼系数的改变则会影响轨桥结构位移振动响应。
在列车以单线三车厢的布置通过桥梁时,仅改变列车一系悬挂刚度系数而其他参数不变时,车-轨-桥耦合系统的振动响应如图4所示。对于车体振动加速度响应,从图4(a~c)可以看出,当列车一系悬挂刚度系数分别为5×105N/m,6×105N/m和7×105N/m时,车体振动加速度在峰值处有微小增加,车体振动加速度幅值无较大改变;通过图4(d~e)钢轨和桥梁振动位移响应可知,车体的一系刚度系数改变对钢轨和桥梁几乎无影响。
3.3 钢轨-轨道板-桥梁的连接(刚度和阻尼)影响
图5为在改变钢轨与轨道板和轨道板与桥梁间的连接参数时,列车、钢轨和桥梁的最大振动响应变化关系。从图5(a~d)可以看出,改变钢轨和轨道板间的离散刚度系数与粘滞阻尼系数和轨道板与桥梁间的连续刚度系数与粘滞阻尼系数时,列车、钢轨和桥梁的最大位移几乎无变化,而且钢轨与桥梁的最大位移保持一致,但钢轨与桥梁的加速度却有所不同,如图5(e~h)所示。随着钢轨与桥梁间连接系数值的增加,钢轨结构最大加速度受其影响程度要大于列车和桥梁结构,列车和桥梁结构的最大加速度几乎无影响。因此,除了钢轨的最大加速度随着连续刚度系数增加呈线性递减外,列车、钢轨和桥梁的振动响应并不易受钢轨与桥梁间连接参数的影响。

表4 单线三车厢耦合系统参数改变对结构的影响(第一节车厢)Tab.4 Influence of the parameter change of the coupling system on the structure of the single -line three -car compartment (the first car)

表5 单线三车厢耦合系统参数改变对结构的影响(第一节车厢)Tab.5 Influence of the parameter change of the coupling system on the structure of the single -line three -car compartment (the first car)
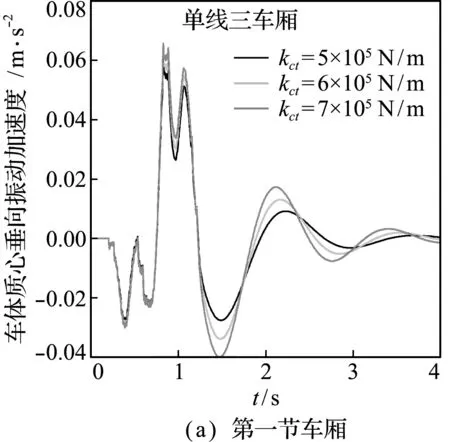
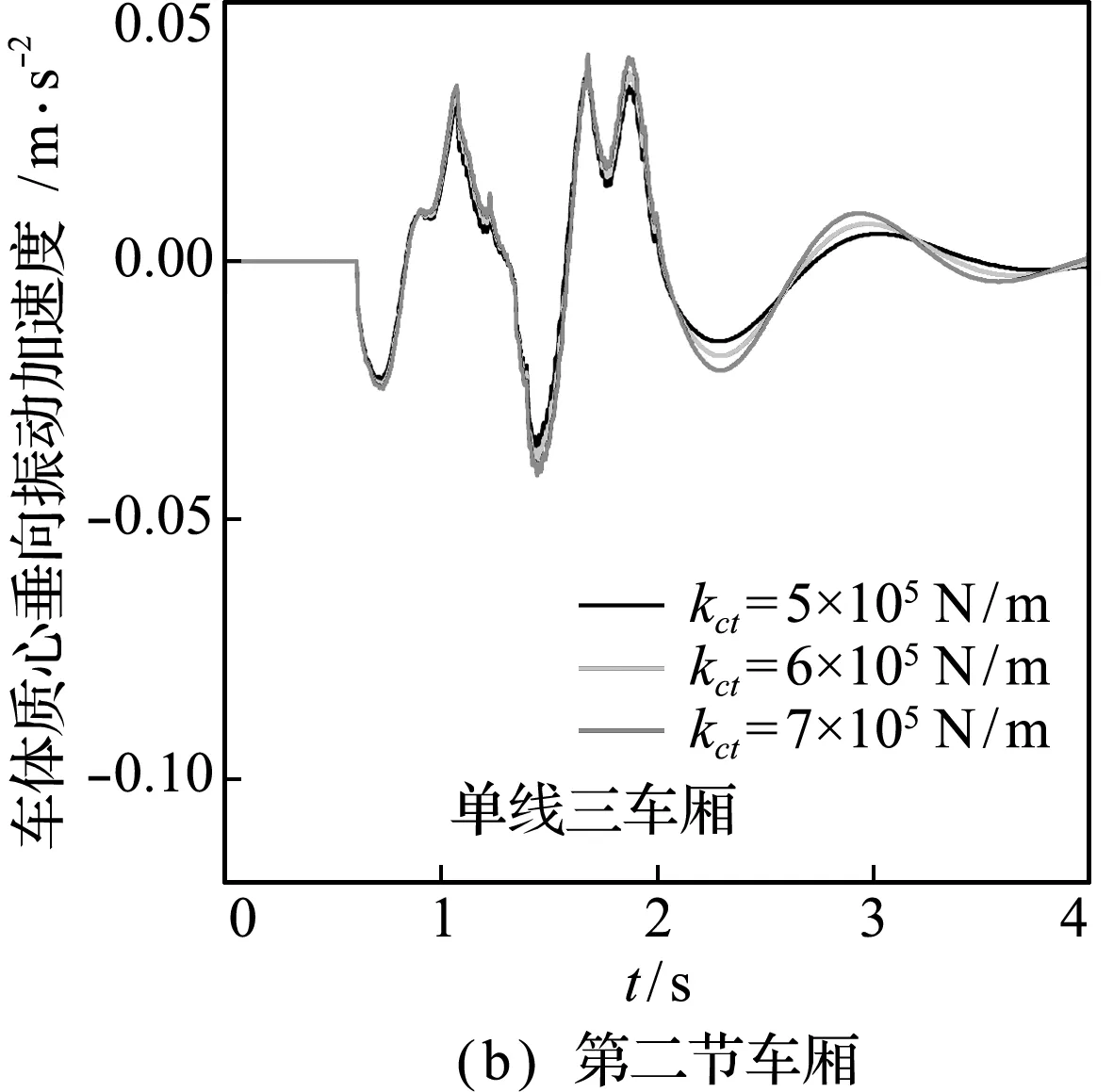
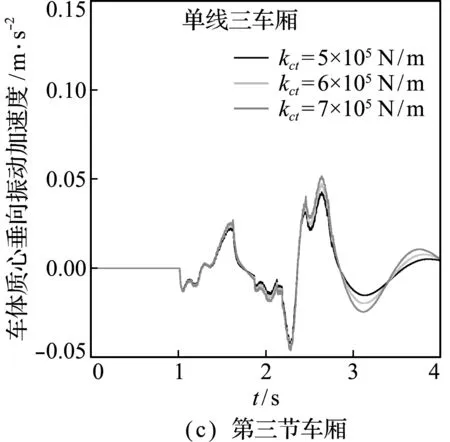
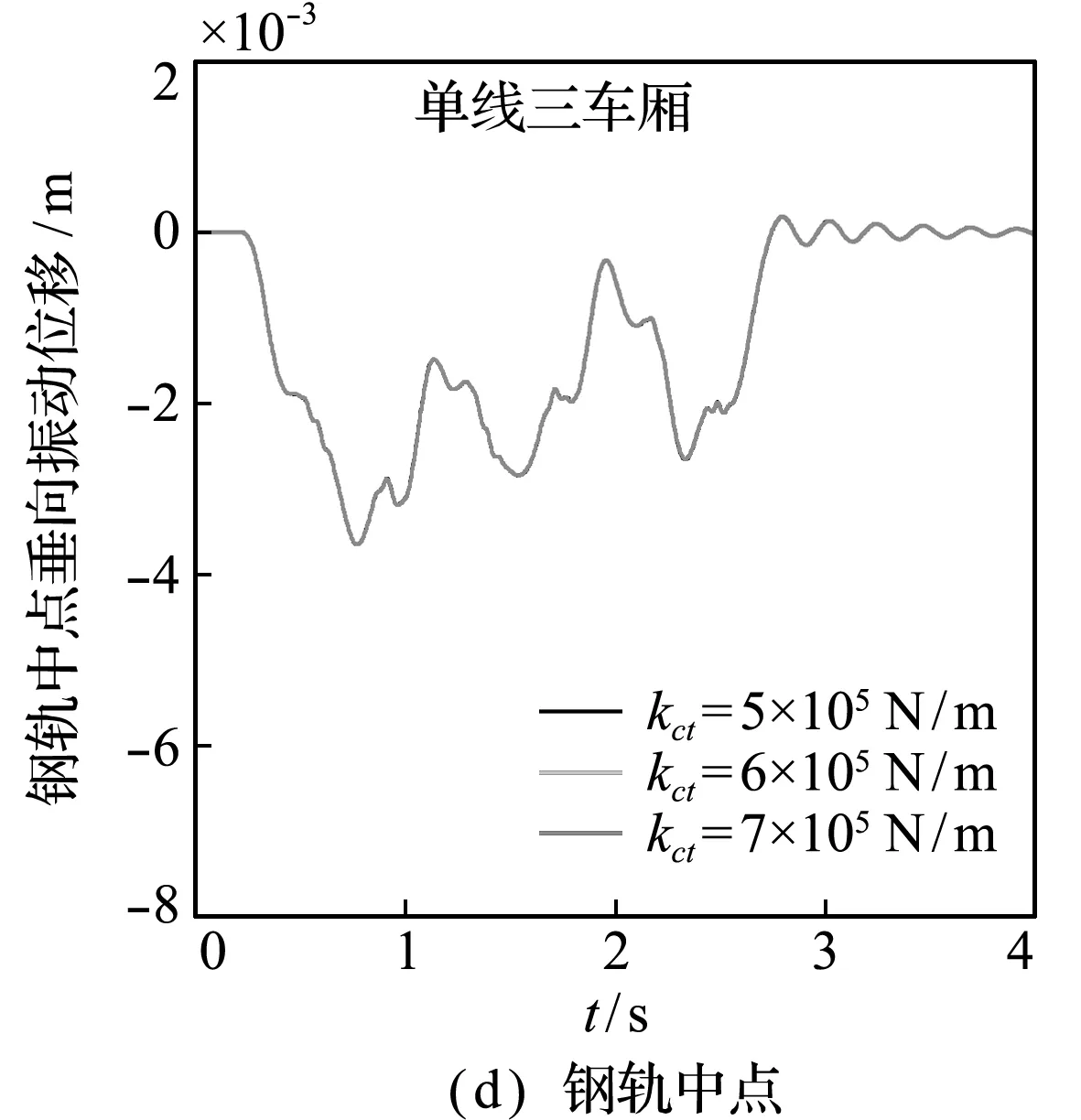

图4 车体一系刚度系数改变时各耦合系统结构的振动响应
Fig.4 Vibration response of each coupling system structure when the primary stiffness coefficient of the car body is changed
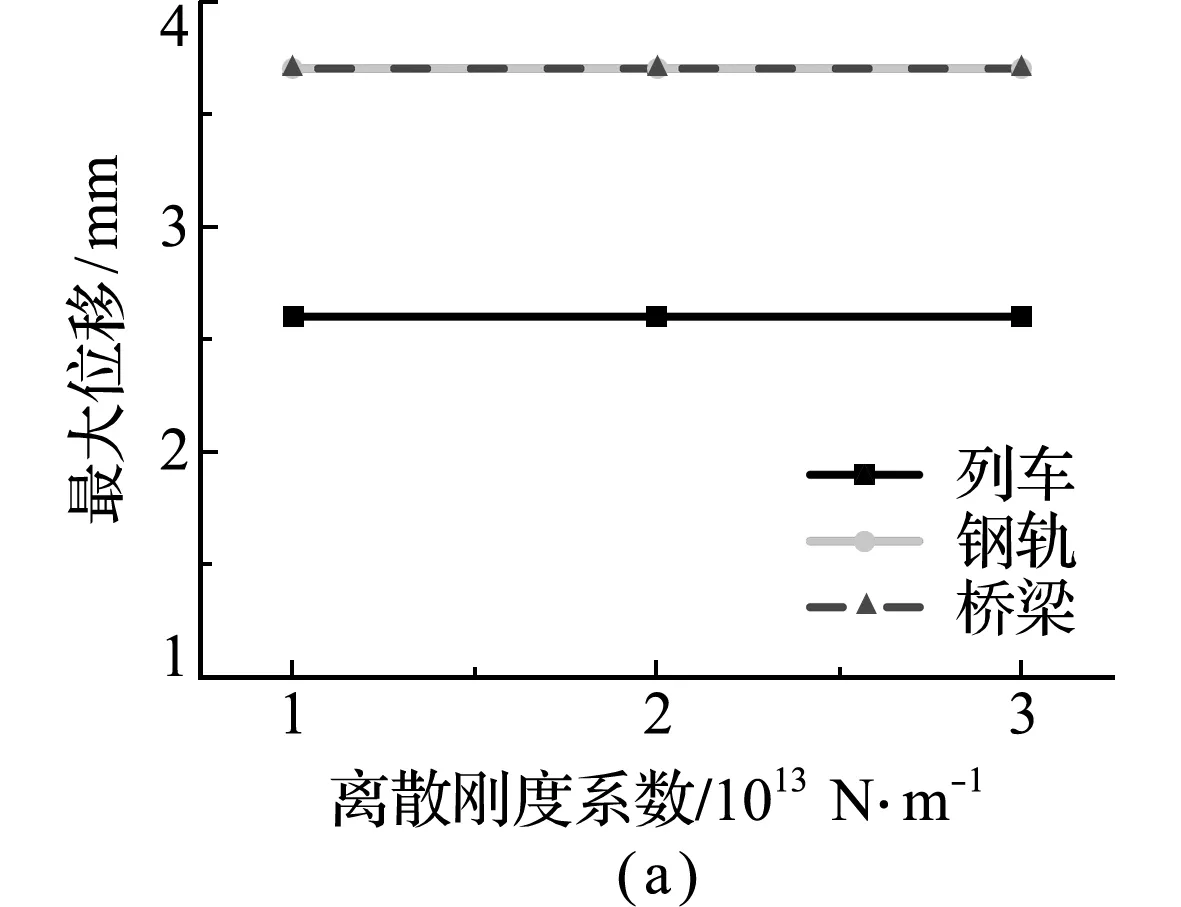
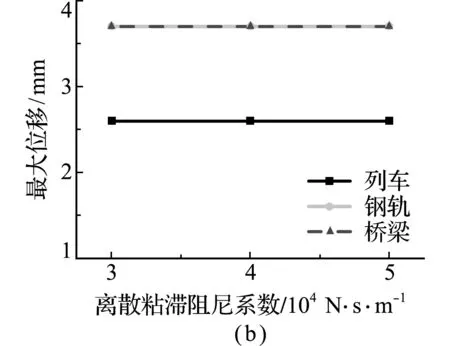

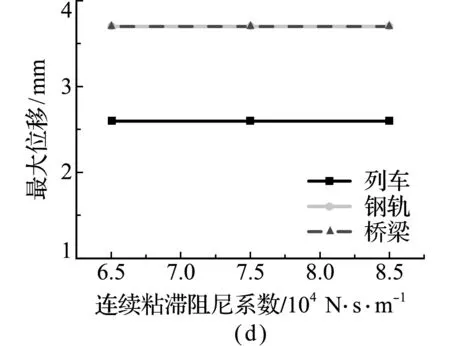
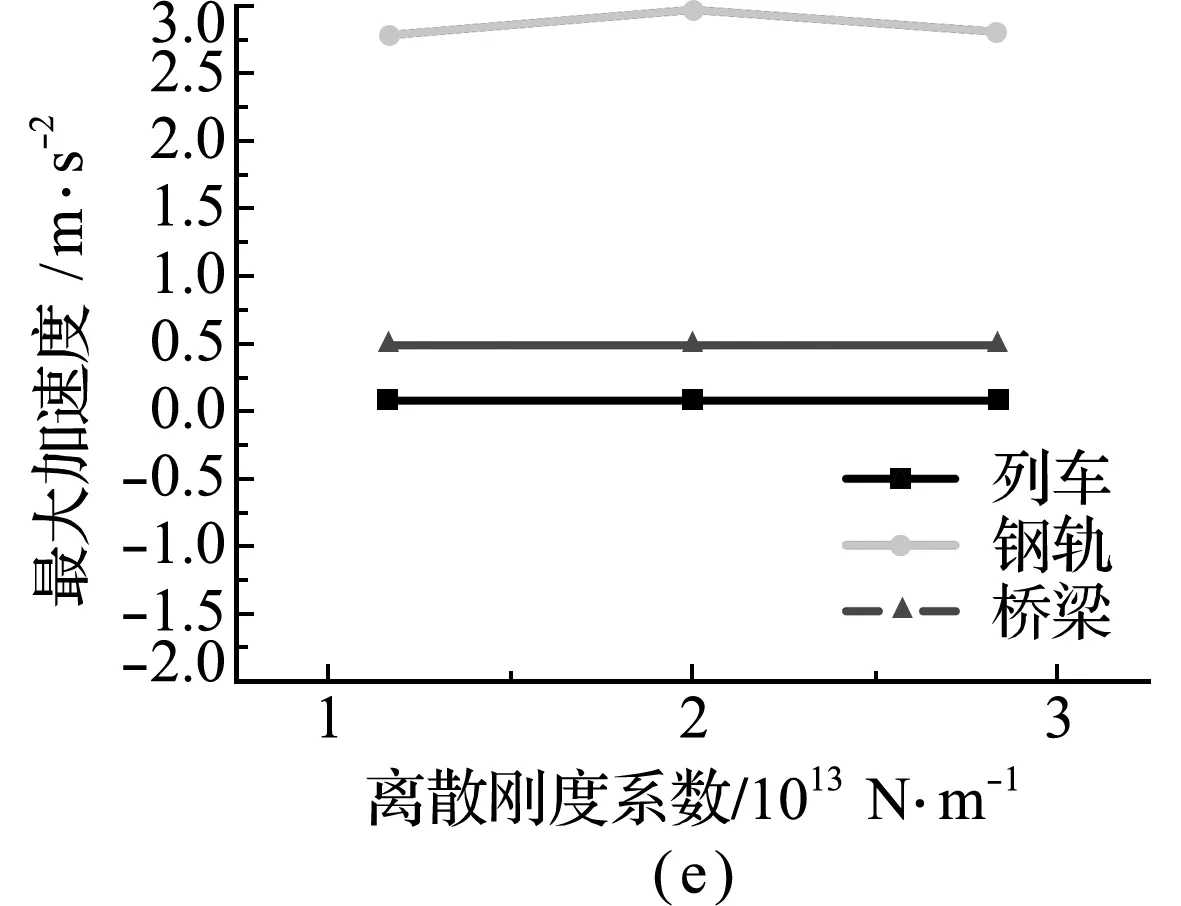
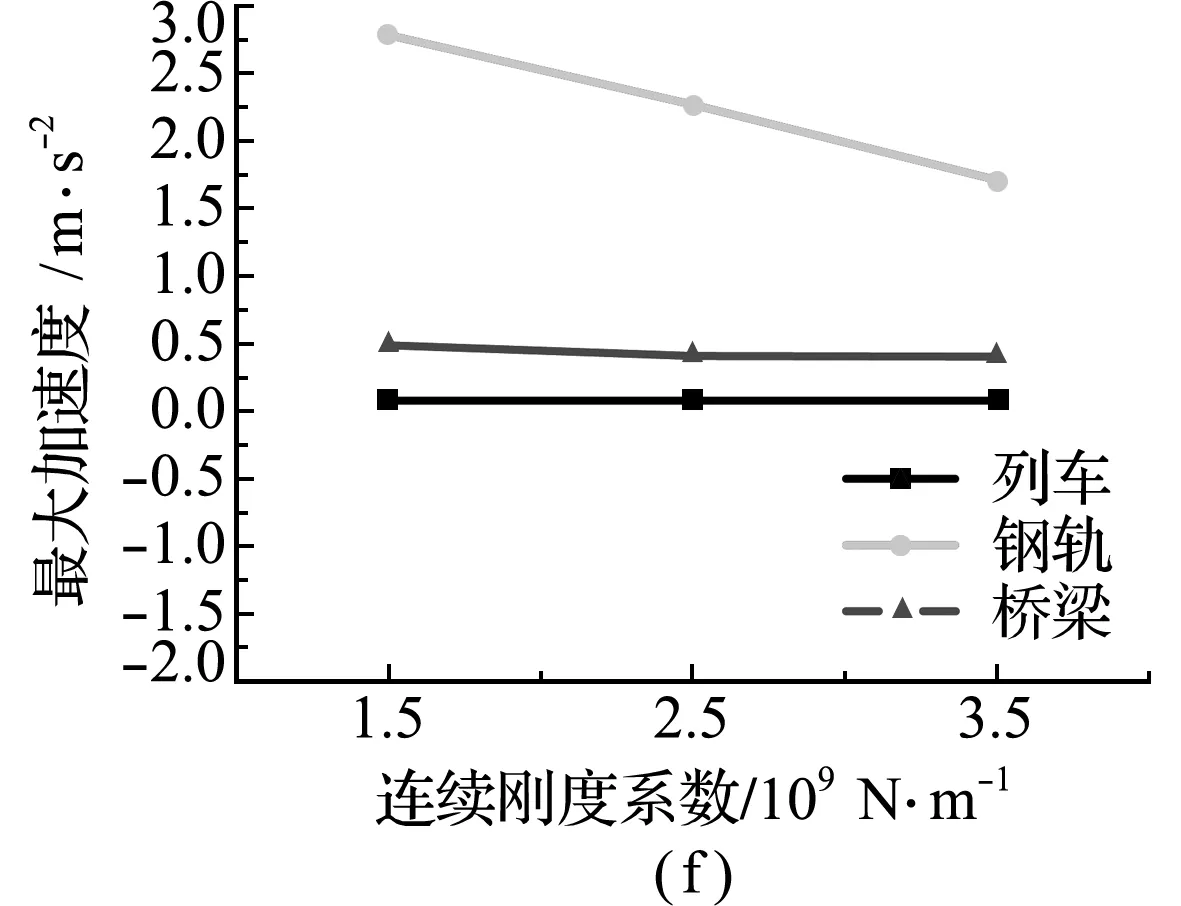
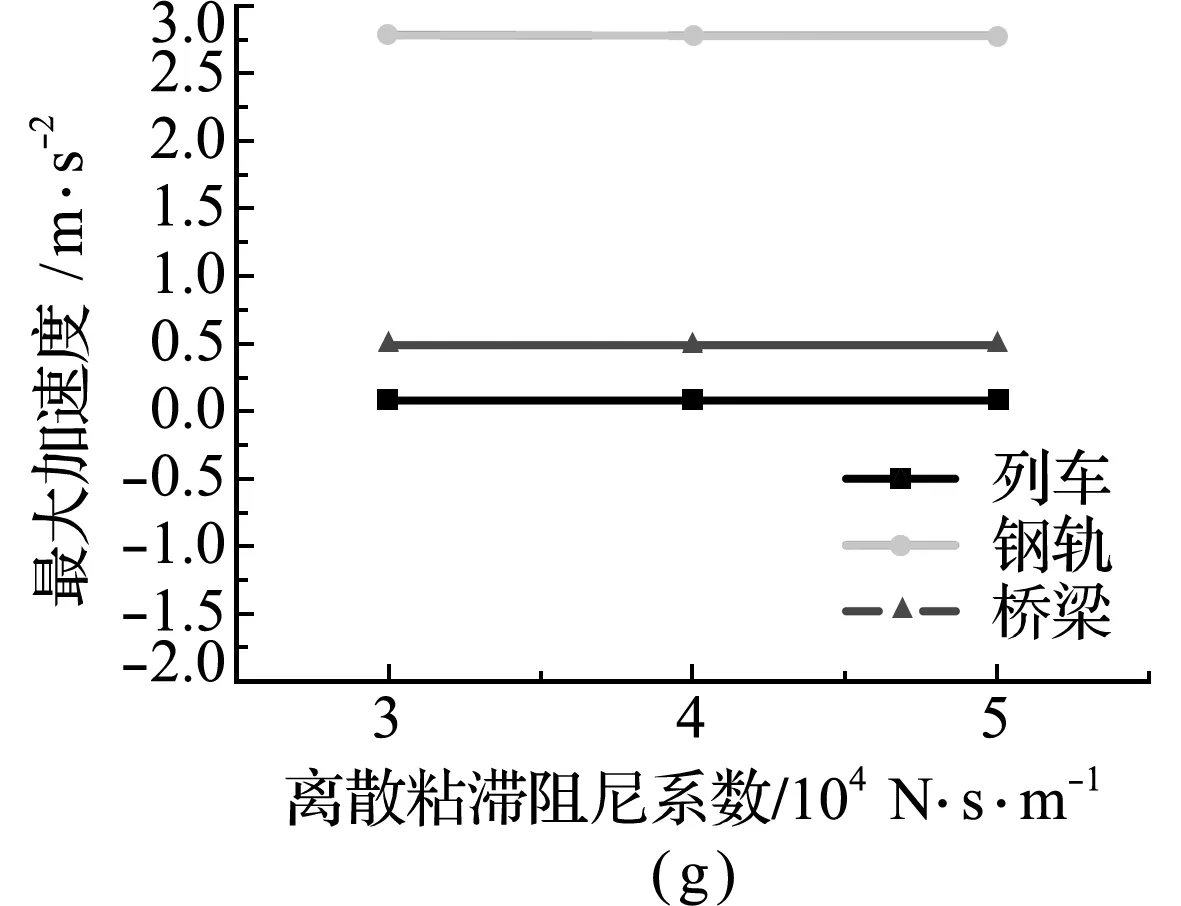
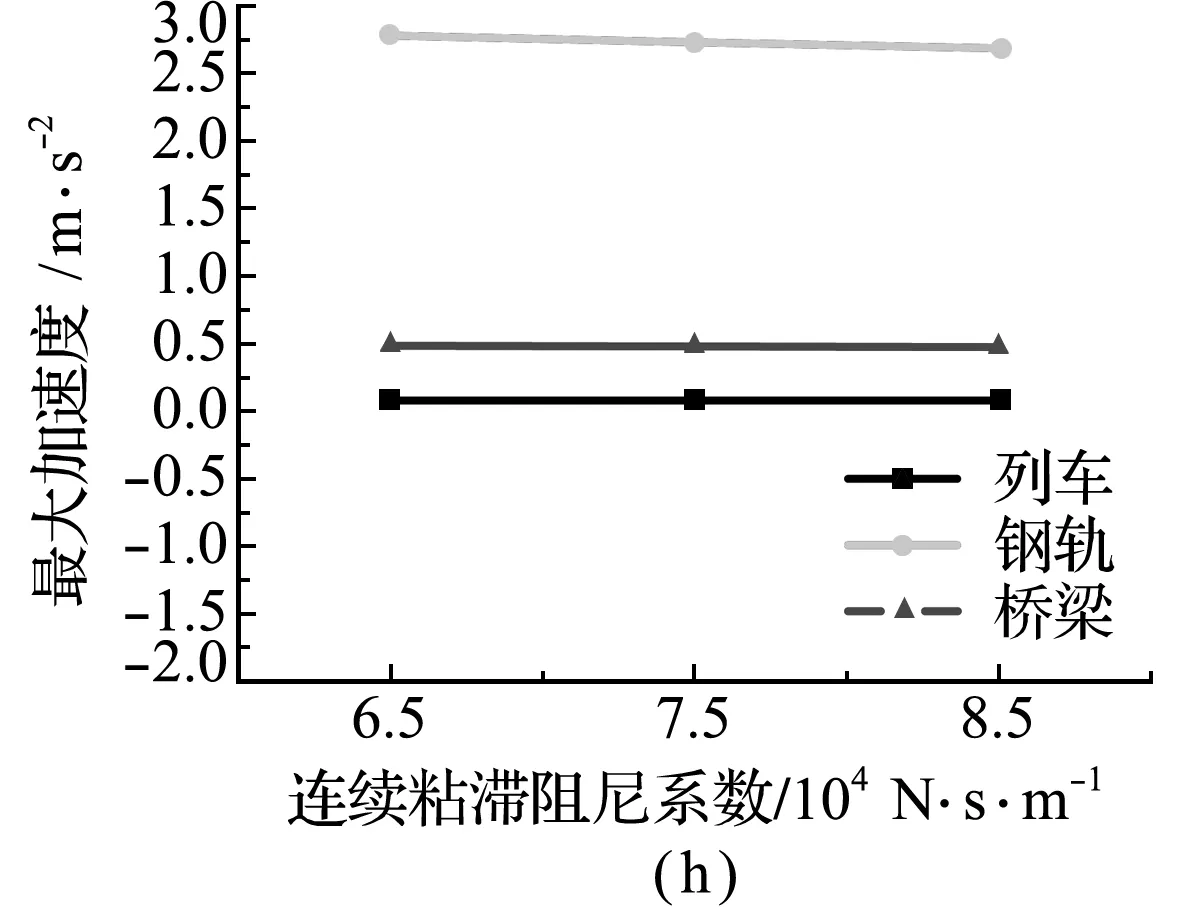
图5 钢轨和桥梁连接系数对耦合系统最大振动响应的影响
Fig.5 Influence of rail and bridge connection coefficient on maximum vibration response of coupling system
4 结 论
本文依据列车、轨道和桥梁间的相互作用关系,建立了列车-钢轨和板式无砟轨道-桥梁耦合系统的运动方程。重点分析了双线列车以不同工况通过高速铁路桥梁时,列车行驶状态(速度和加速度)、列车悬挂系数以及钢轨与桥梁连接参数对列车、轨道和桥梁动力学性能的影响,得出以下结论。
(1) 列车悬挂参数的改变对列车自身结构影响较大,而对钢轨和桥梁结构几乎无影响。
(2) 随着列车速度与加速度在一定范围内的增加,车体自身结构的位移振动响应在逐渐减小,而钢轨和桥梁结构的位移振动响应则在不断增加。
(3) 车体一系刚度系数增大会引起列车系统结构振动响应变大,但车体二系刚度系数的增加却抑制了车体结构的振动响应。
(4) 除了钢轨的最大加速度随着连续刚度系数增加呈线性递减外,列车、钢轨和桥梁的振动响应并不易受钢轨与桥梁间连接参数的影响。
