车辆悬架控制臂液压衬套区间动刚度模型研究

2020-05-23於孝朋郑红梅王海朔张国军

计算力学学报 2020年2期

陈科，於孝朋，郑红梅，王海朔，张国军，吴睿

(合肥工业大学机械工程学院，合肥 230009)

1 引言

车辆悬架控制臂液压衬套主要用于控制臂的减振，对橡胶衬套进行封装液体处理，可变为液压衬套，其结构和原理类似发动机的液压悬置[1-3]。传统的悬架控制臂减振中，常用橡胶衬套；然而，对于低频大振幅的振动，需要大阻尼进行减振，橡胶衬套难以满足要求。因此，液压衬套在悬架控制臂上的应用越来越多。文献[4]开发了一种带有磁铁和线圈的液压衬套模型，可以实现半主动控制，其借鉴了液压减振器与磁铁和线圈结合形成磁流变减振器的方法。文献[5]设计了液压衬套的防漏装置。文献[6]通过理论和实验方法对液压衬套的瞬态响应进行了研究，理论模型获得的瞬态响应曲线与实验曲线基本吻合，验证了理论模型的正确性。文献[7]分别对轴向外部载荷和径向外部载荷作用的液压衬套动态性能进行了集总参数模型的数学建模，并利用实验验证了模型的正确性。文献[8,9]设计了一种具有长短通道的双通道液压衬套，分别对其时域响应和频域响应进行了研究。文献[10]对不同路面的行驶舒适度和液压衬套的相关性进行了分析。文献[11,12]建立了非线性状态下的液压衬套动态响应数学模型，并研究了其动态响应变化规律。文献[13]通过实验结果对非线性状态下的动态响应数学模型进行了验证。基于液压衬套的非线性状态研究成果，文献[14]开发出一种正弦外载和瞬态外载共同作用下的非线性数学模型。文献[15]对设计参数和滞后角损耗之间的关系进行了数学建模，并通过实验数据对理论模型进行了验证。

上述研究中，没有对动刚度的上界限和下界限变化曲线进行研究；且将流体惯性系数和流量阻尼系数作为确定量，获得的动刚度结果与工程实际有一定差异。为了全面和客观地描述动刚度，本文引入区间不确定性理论。流体惯性系数和流量阻尼系数与液压衬套的惯性通道结构、惯性通道材料性能和流体性能等诸多因素相关，非常复杂。因此，本文将流体惯性系数和流量阻尼系数定义为区间变量以获得区间动刚度模型，使用子区间组合法对区间动刚度进行优化。

2 基础理论

2.1 区间不确定性理论

本文的基础理论包括区间数学和液压衬套传统动刚度模型。对于一些信息缺乏程度高的参量，可以将其作为区间变量处理。运用区间数学理论(即区间不确定性理论)对含有区间变量的函数或者方程组进行运算，可以为工程实践提供良好的指导。根据文献[16,17]，可以给出表达式(1～3)。

A为区间数，定义为

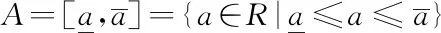
(1)

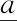
区间数A的中点和宽度为

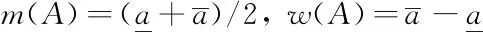
(2)

式中m表示区间数A的中点，w表示区间数A的宽度。

区间数A可以用中点和宽度来表示为

A=[m(A)-w(A)/2,m(A)+w(A)/2]=

[m(A);rad(A)]

(3)

式中 rad(A)=w(A)/2，表示区间半径。

文献[16,17]对区间数的算术运算、逻辑运算、数乘运算、指数运算、对数运算和幂运算等进行了详细论述。区间数间的运算满足加法结合律、乘法结合律、加法交换律和乘法交换律。但是，两个区间运算不一定满足分配律；而且，相同区间数相减不一定等于零区间。区间函数和区间方程组运算可能会出现区间扩张，原因为参数多次参与运算。目前，区间扩张的解决方法主要有运算顺序处理法、截断处理法、子区间摄动处理法和子区间组合处理法等。尤其，当涉及到非线性区间方程组时，区间扩张的处理将相当复杂。

2.2 液压衬套传统动刚度模型

车辆悬架控制臂液压衬套用于控制臂减振，液腔间的压力差产生阻尼力，对流经惯性通道的流体做功从而削减振动。液压衬套主要由外管、内管、金属骨架、限位块、橡胶主簧和液腔等组成，其结构如图1所示。

图2为悬架控制臂液压衬套的简化物理模型，液腔简化为弹簧阻尼系统，橡胶主簧也简化为弹簧阻尼系统。图2中，P1和P2表示液腔压力，S表示等效活塞面积，k1和c1表示橡胶主簧的刚度和阻尼，k2和c2表示上端液腔的刚度和阻尼，k3和c3表示下端液腔的刚度和阻尼，xs表示等效活塞位移，x(t)表示金属内管位移，F(t)表示金属内管受载。

文献[19]给出了单惯性通道液压衬套径向受载动刚度的详细建模过程，所建模型为表达式(4，5)。悬架控制臂液压衬套理论研究一般忽略流经惯性通道流体的非线性状态。

图1 液压衬套结构[18]

Fig.1 Structure of hydraulic bushing

(4)

式中Ka为悬架控制臂液压衬套的存储动刚度，Kb为悬架控制臂液压衬套的损失动刚度，ω为液压衬套振动圆频率，S为封闭液室的等效活塞面积，ke为两个封闭液室的等效体积刚度系数，ce为两个封闭液室的等效体积阻尼系数，i为流经液压衬套惯性通道的流体惯性系数，r为流体线性流动的流量阻尼系数。

悬架控制臂液压衬套的动刚度为

(5)

式中Kd为液压衬套的动刚度。

液压衬套传统动刚度模型仅将流体惯性系数和流量阻尼系数两个输入变量作为确定量。然而，流体惯性系数和流量阻尼系数与液压衬套的惯性通道结构、惯性通道材料性能和流体性能等诸多因素相关，非常复杂；且获取这两个变量数值的信息相当缺乏。仅将两个变量作为确定量，会使得获得的输出量(即动刚度)与工程实际差异较大。因此，需要采用区间变量来描述流体惯性系数和流量阻尼系数，通过建立区间模型来获得区间动刚度，实际动刚度值将处于区间动刚度内。

3 液压衬套区间动刚度模型

3.1 无精度要求时的区间动刚度模型

一般通过工程经验或者实验来辨识流体惯性系数i和线性流动流量阻尼系数r的数值。其中存在诸多难以控制的误差因素，难以保证精确度。获取关于这两个系数数值的精确信息量相当缺乏，如是否为随机变量及能否获知概率分布；所以，采用区间变量来描述较好。

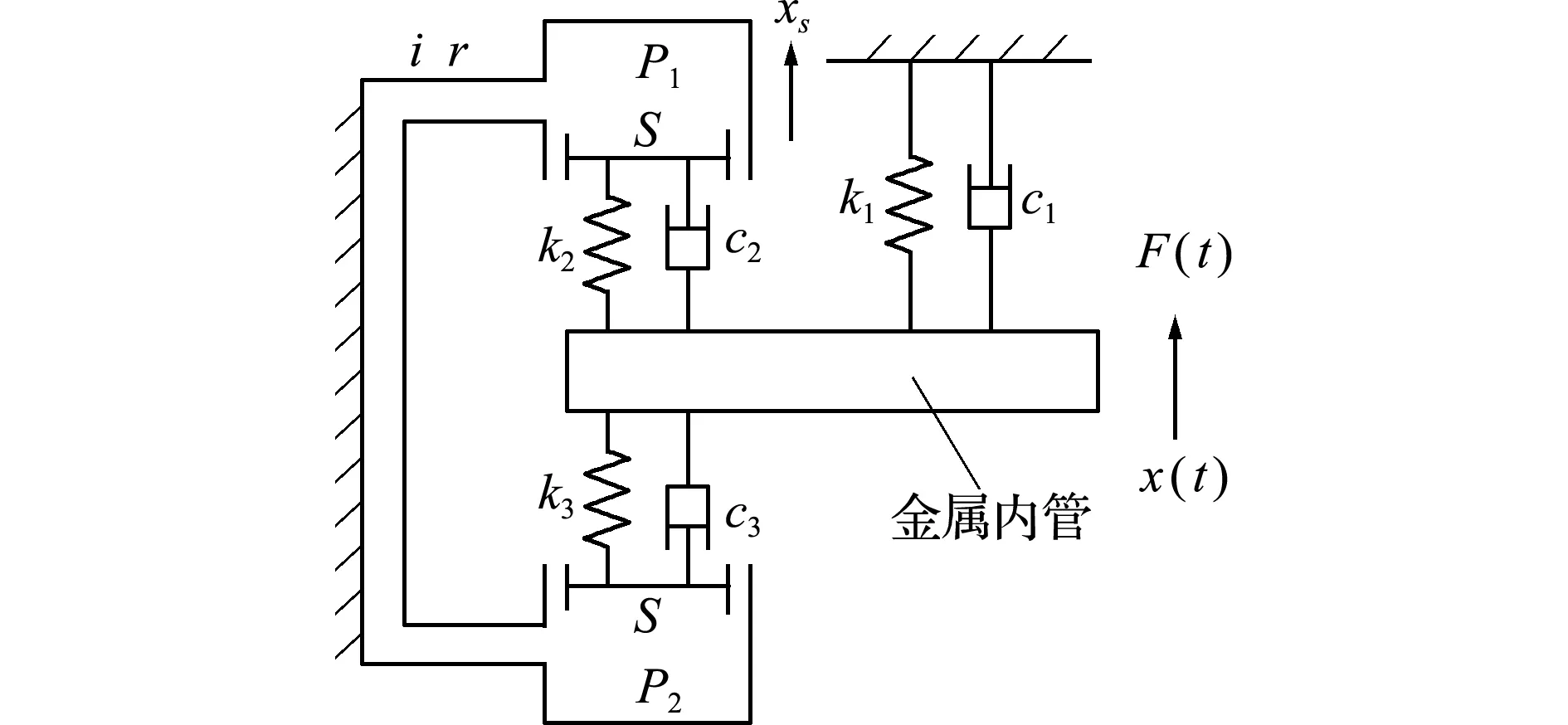
图2 液压衬套物理模型[19]

Fig.2 Physical model of hydraulic bushing

本文将流体惯性系数i和线性流动流量阻尼系数r作为区间变量，运用区间不确定性理论来建立悬架液压衬套动刚度的区间数学模型。

为了便于运算，用h1，h2，h3，h4，h5和h6替换Ka和Kb的部分表达式：

h3=i2ceω4，h4=cer(ce+r)ω2

(6)

用f1，f2，f3和f4替换Ka和Kb的部分表达式得

f1=h1-h2,f2=h3+h4+h5

f3=f1/h6,f4=f2/h6

(7)

式(4)的Ka和Kb可以改为

Ka=k1+S2ω2f3,Kb=c1ω+S2ωf4

(8)

对于区间数A和B，相互间的算术运算为[16,17]

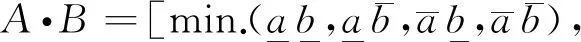
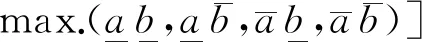
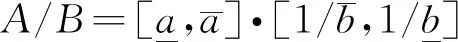
(9)

区间变量iI和rI的表达式为

(10)

根据式(9)，区间变量h1I的运算过程为

(11)

(12)

同理，根据区间数算术运算式(9)，h2I，h3I，h4I，h5I，h6I，f1I，f2I，f3I和f4I的表达式为

(13)

(14)

(15)

(16)

(17)

(18)

(19)

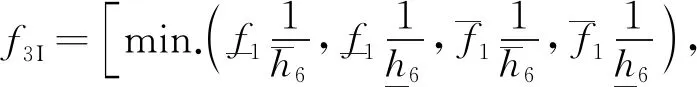
(20)

(21)

因此，KaI和KbI的表达式为

(22)

悬架控制臂液压衬套的区间变量动刚度Kd I为

(23)

区间动刚度Kd I的中点处动刚度为

(24)

3.2 一定精度要求下的区间动刚度优化模型

区间计算常会导致区间扩张，区间扩张对区间动刚度的运算会产生不良影响，区间精度可以用来描述区间扩张。为了获得满足区间精度要求下的区间动刚度，采用文献[17]的子区间组合法来进行研究。区间变量iI和rI分割为多个子区间，可以获得一定精度要求下的区间动刚度Kd I。

区间变量流体惯性系数iI的子区间为

⋮

(1≤n≤N)(25)

式中iIn表示区间变量iI划分的子区间名称，如iI 1表示第一个子区间；w(iI)表示区间变量iI的区间宽度，N表示区间变量iI划分的子区间数目。

区间变量线性流动流量阻尼系数rI的子区间为

⋮

(1≤n≤N)(26)

式中rIn表示区间变量rI划分的子区间名称，如rI 1表示第一个子区间；w(rI)表示区间变量rI的区间宽度，N表示区间变量rI划分的子区间数目。

经过子区间组合法的处理，悬架控制臂液压衬套的区间变量动刚度Kd I的精确表达式为

Kd I(iI,rI)=Kd I1(iI1,rI 1)∪Kd I2(iI 2,rI 2)∪

Kd I 3(iI 3,rI 3)…∪Kd I n(iI n,rI n)

(27)

式中Kd I(iI,rI)表示区间变量iI和rI为区间自变量，Kd I为区间函数；Kd I n(iI n,rI n)表示区间变量iI n和rI n为区间自变量，Kd I n为区间函数。动刚度子区间Kd I n(iI n,rI n)可以通过第3.1节的模型计算。

根据文献[17]对区间精度的定义和证明，悬架控制臂液压衬套的区间动刚度Kd I区间精度表达式为

(28)

式中w(Kd I)表示区间变量Kd I的宽度；N表示区间变量iI和rI划分的子区间数目；w(Kd I)|N表示当区间变量iI和rI划分的子区间数目为N时，区间变量Kd I的宽度。

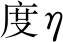
4 区间动刚度模型的验证

4.1 基于实验结果的区间动刚度模型验证

文献[19]进行了动态刚度实验，如图3所示,实验设备为电液振动实验台，型号为MTS831，激励的振动幅度为0.1 mm。图4为实验结果，可以用来验证区间动刚度模型。车辆悬架控制臂液压衬套数学模型的算例变量和数值列入表1[19]。

图3 动刚度实验[19]

Fig.3 Dynamic stiffness experiment

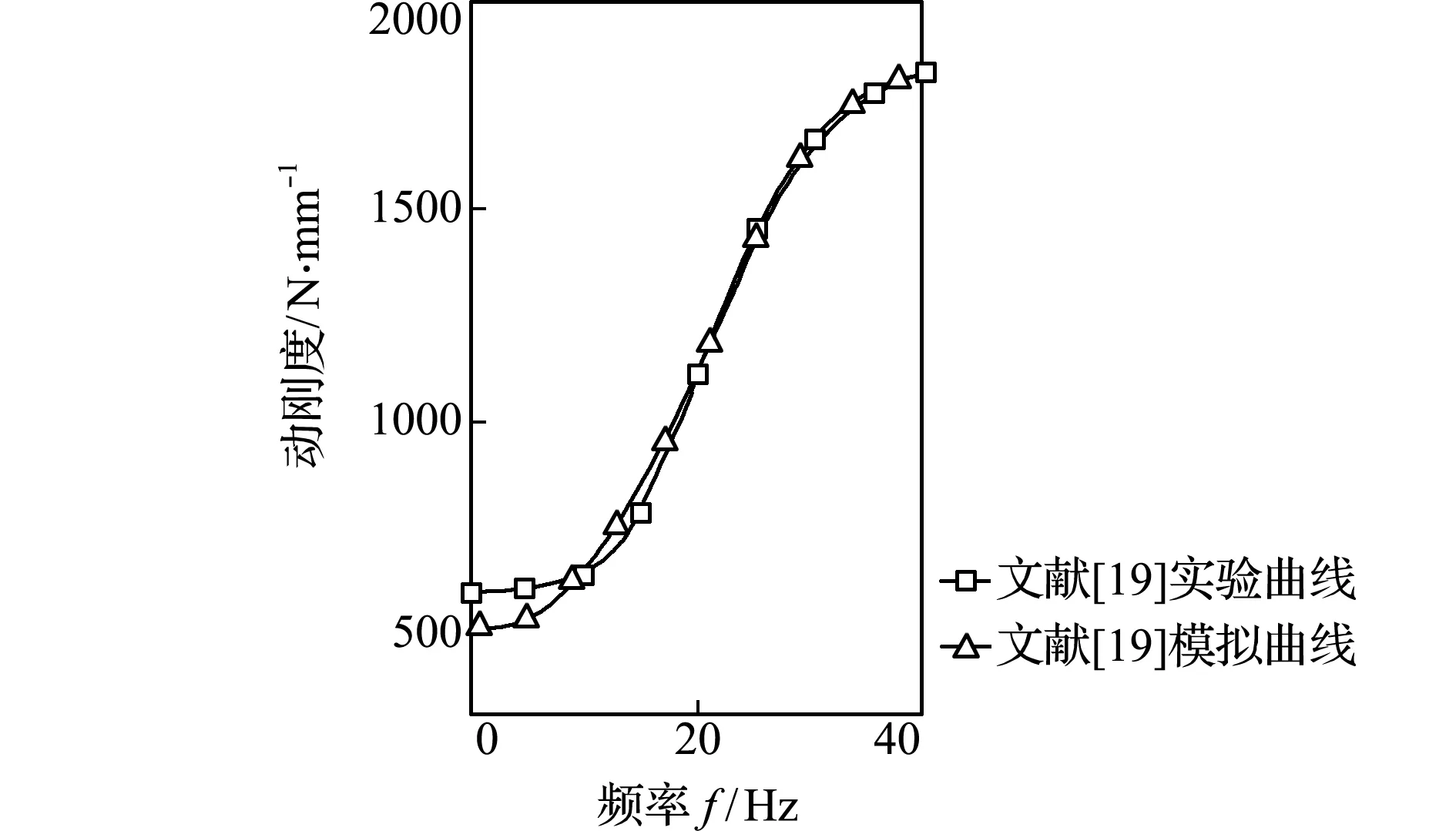
图4 动刚度随频率变化[19]

Fig.4 Variation of dynamic stiffness with vibration frequency

根据建立的区间动刚度数学模型，对表1算例进行运算；频率的变化范围为0 Hz～40 Hz，在Matlab软件中编制程序进行运算，可以获得区间中点的动刚度随振动频率变化规律，如图5所示。区间中点动刚度见式(24)，来源于区间动刚度模型；因此，当区间中点动刚度变化曲线正确时，则区间动刚度模型的推导过程正确。

为了便于比较，将图4和图5的曲线合并到图6。可以看出，区间中点的动刚度曲线非常接近实验曲线。因此，区间中点动刚度是正确的。区间中点动刚度来自区间动刚度模型，故可以确定区间动刚度模型的推导过程是正确的。

4.2 区间动刚度模型的意义

(1) 不考虑区间精度时的区间动刚度曲线

根据未考虑精度的区间动刚度模型，在Matlab中编制程序，可以获得表2结果，即不同频率下的区间动刚度Kd I和区间动刚度宽度w(Kd I)值。根据传统动刚度模型和表2，可以获得图7结果。

表1 算例变量和数值

Tab.1 Variables and values of example

变量数值流体惯性系数名义值E(i)/N·s2·m-51.33×104流体惯性系数下界i0.95E(i)流体惯性系数上界i1.05E(i)流量阻尼系数名义值E(r)/N·s·m-52.46×106流量阻尼系数下界r0.95E(r)流量阻尼系数上界r1.05E(r)橡胶主簧刚度k1/N·m-15×105橡胶主簧阻尼c1/N·s·m-1100液腔等效体积刚度ke/N·m-54.8×108液腔等效体积阻尼ce/N·s·m-52.77×105等效活塞面积S/m24.6×10-2

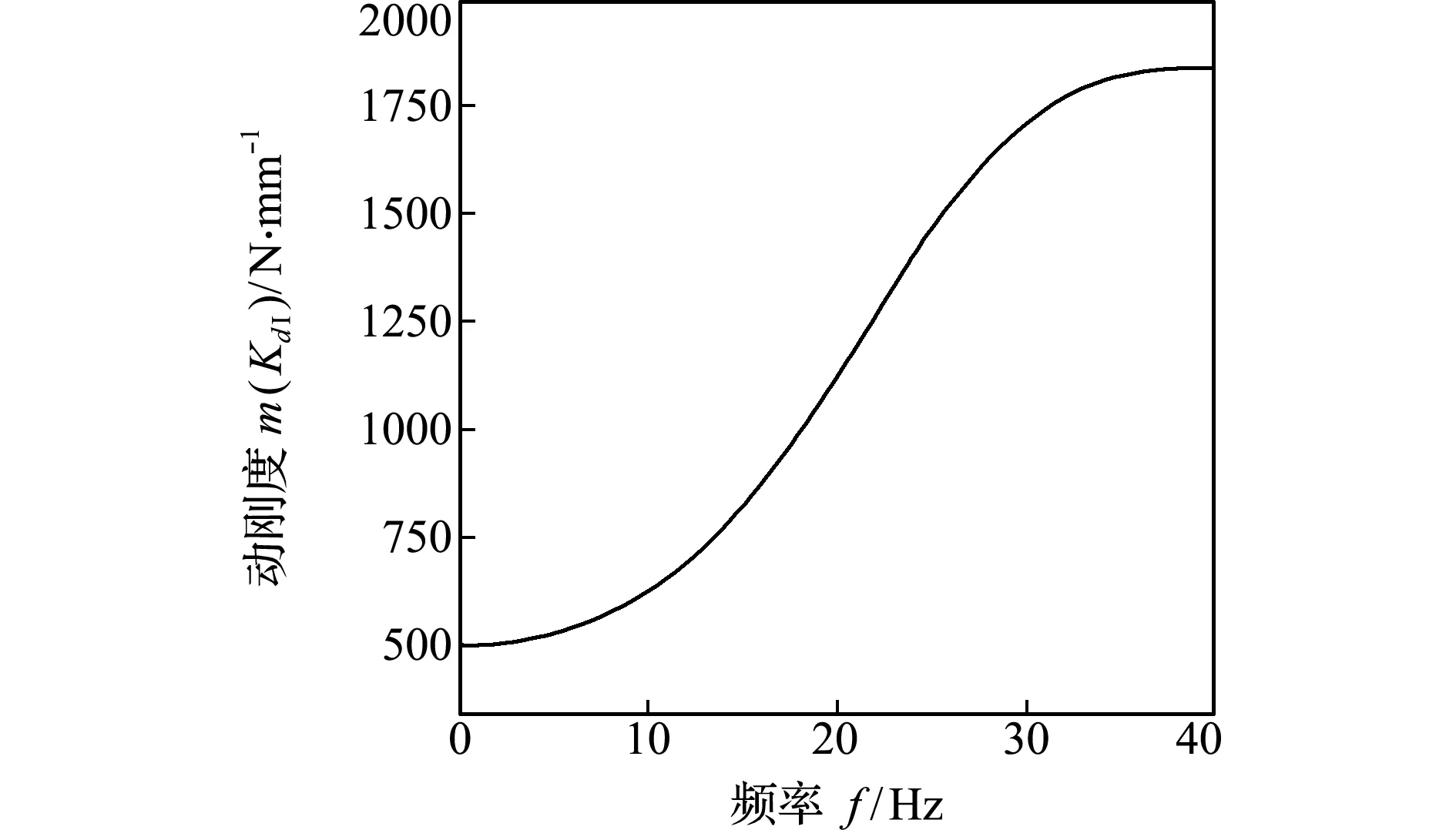
图5 区间中点的动刚度随频率变化

Fig.5 Dynamic stiffness of interval middle point varies with frequency

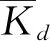
(2) 考虑区间精度时的区间动刚度曲线优化

图6 区间中点动刚度曲线、实验曲线和模拟曲线

Fig.6 Dynamic stiffness curves of the interval middle point,the experiment and the simulation

表2 不考虑精度时的Kd I和w(Kd I)数值

Tab.2 Values ofKd Iandw(Kd I) without precision requirement

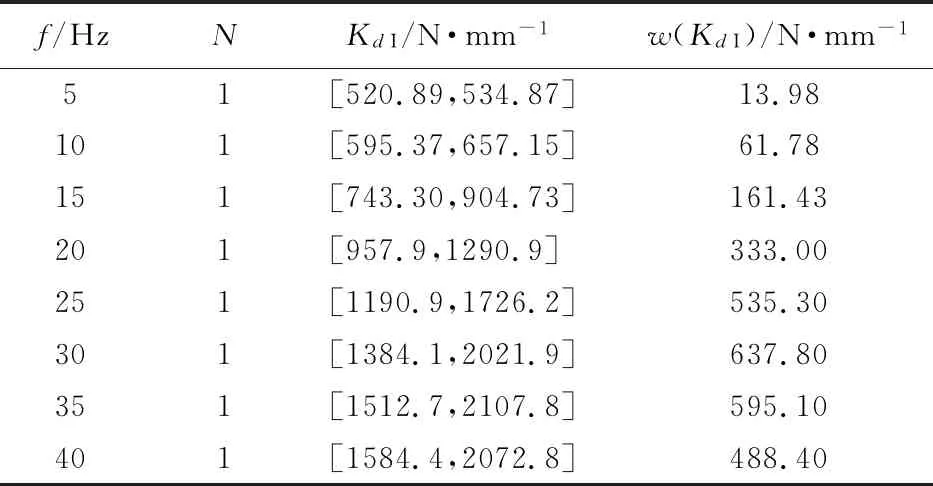
f/HzNKdI/N·mm-1w(KdI)/N·mm-151[520.89,534.87]13.98101[595.37,657.15]61.78151[743.30,904.73]161.43201[957.9,1290.9]333.00251[1190.9,1726.2]535.30301[1384.1,2021.9]637.80351[1512.7,2107.8]595.10401[1584.4,2072.8]488.40

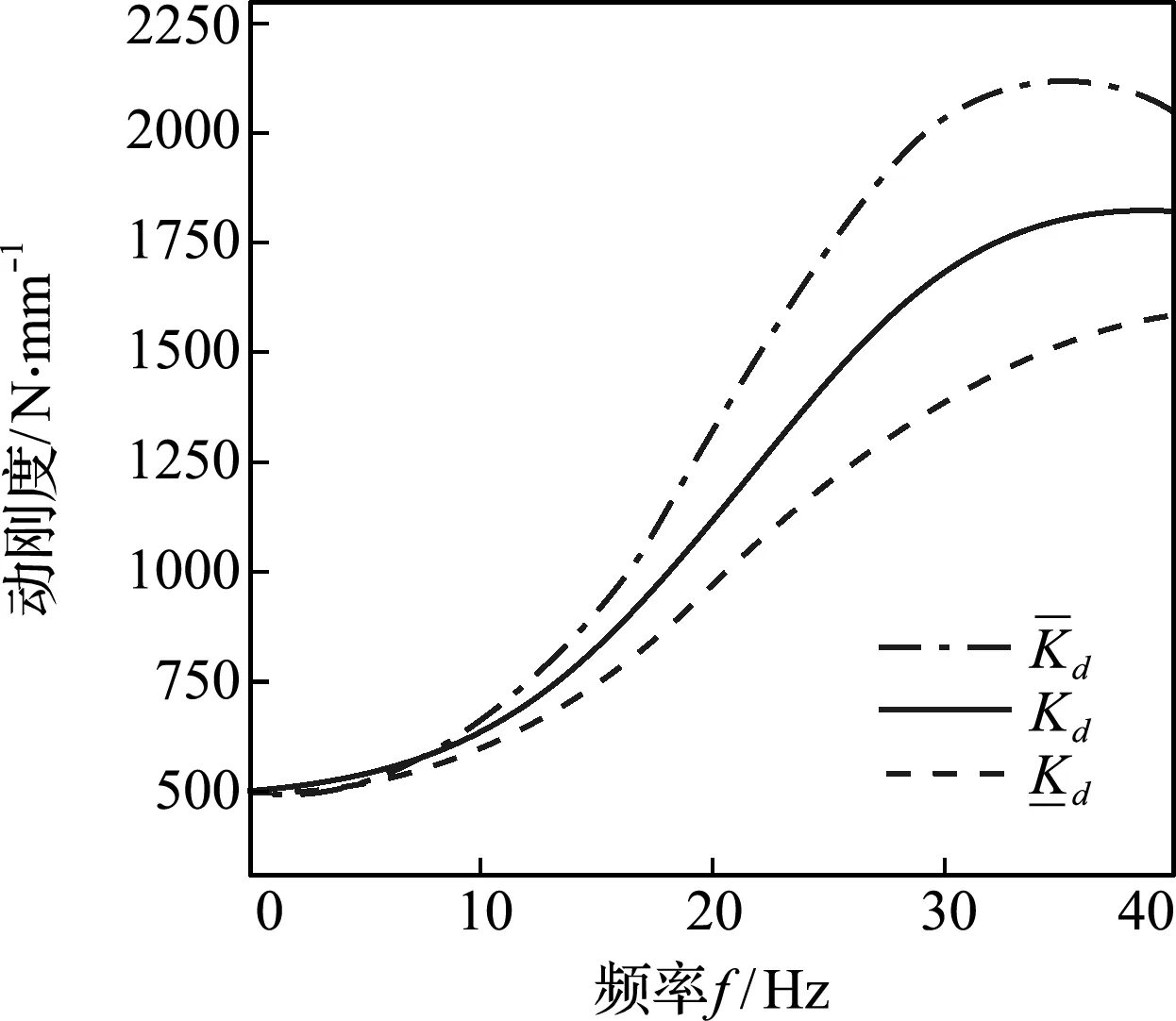
图7 文献[19]的模型和区间模型计算的动刚度随频率变化

Fig.7 Variation of the dynamic stiffness from the model of Ref.[19] and the interval model with frequency

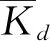
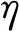
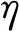
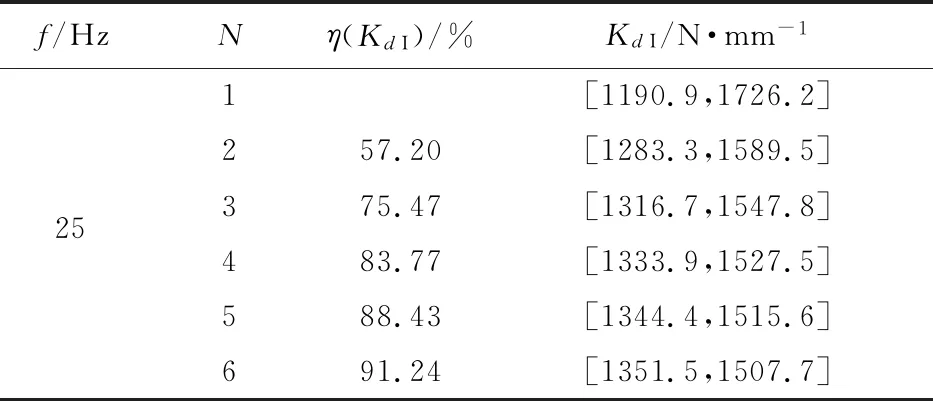
f/HzNη(KdI)/%KdI/N·mm-11[1190.9,1726.2]257.20[1283.3,1589.5]25375.47[1316.7,1547.8]483.77[1333.9,1527.5]588.43[1344.4,1515.6]691.24[1351.5,1507.7]

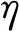
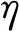
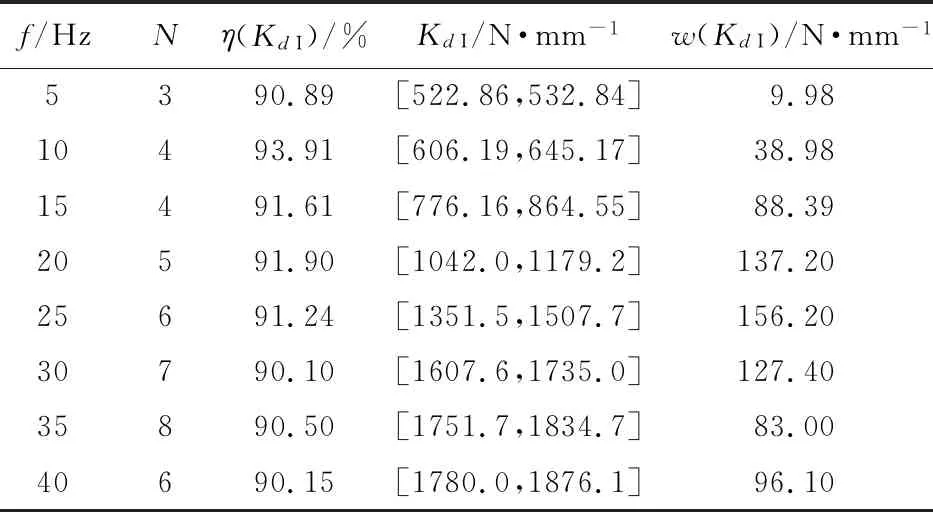
f/HzNη(KdI)/%KdI/N·mm-1w(KdI)/N·mm-15390.89[522.86,532.84]9.9810493.91[606.19,645.17]38.9815491.61[776.16,864.55]88.3920591.90[1042.0,1179.2]137.2025691.24[1351.5,1507.7]156.2030790.10[1607.6,1735.0]127.4035890.50[1751.7,1834.7]83.0040690.15[1780.0,1876.1]96.10