基于塑性铰理论的车身概念设计正碰分析与优化方法

耿富荣，朱晋甫，赵永宏，李健华，侯文彬*

(1.广州汽车集团股份有限公司汽车工程研究院，广州 511434；2.大连理工大学 工业装备结构分析国家重点实验室 汽车工程学院，大连 116024)

1 引 言

近年来，我国汽车工业经历了高速发展的阶段。2017年，全年汽车产销2901.5万辆和2887.9万辆，连续9年蝉联全球第一。随着汽车设计水平的逐步提高，汽车企业迫切需要缩短设计周期,快速推出新车型，以抢占细分市场，获取更大的利润。车身作为汽车四大总成之一，是保证汽车性能的主要载体，是汽车设计的重要组成部分。车身结构设计的初始阶段即概念设计阶段，目标主要为在总体上确定车身的结构布置和各项性能指标，而不考虑细节设计，此阶段将确定汽车成本的70%，设计影响占到汽车总体设计的60%，自由度较大；详细设计中将完成每一部件的完整几何定义，越到设计后期，设计的自由度越小，修改设计的成本越高。因此，研究车身概念设计的关键技术对于提高车身性能和缩短设计周期具有重要意义。结构耐撞性作为评价车身安全性能的重要指标，其设计的难度很大，目前多在详细设计阶段考虑，若出现问题，重复设计的工作成本大幅提高。因此在概念设计阶段考虑车身的耐撞性能，对车身设计的发展有重要 意义。

国外的一些研究院所和大型汽车厂商首先针对概念设计开展了相关研究工作。Reed[1]应用Optistruct优化软件进行白车身概念设计，包括车身拓扑优化、梁单元建立以及梁结构耐撞性优化。Liu等[2-4]系统性研究了多种截面薄壁直梁的耐撞性简化方法，推导了计算溃缩特性和弯曲特性曲线的公式，提出了应用梁单元与非线性弹簧组合模拟塑性铰的方法，并建立了简化的梁单元模型进行碰撞分析，与详细模型对比分析，发现此简化方法有较高的精度。Nishigaki等[5]开发了一种专用于车身概念设计的FOA系统，该系统可用于接头分析、截面性能计算和NVH分析等，对参数化的梁单元进行碰撞分析。

国内对车身概念设计的研究工作较少，主要集中在概念模型的建立和NVH静态性能等方面的研究，对概念模型的碰撞和吸能构件的耐撞性研究分析较少。胡平等[6-8]开发了基于NX的智能车身概念设计工具IVCD，输入车身基本信息即可快速建立参数化车身概念几何模型和有限元模型，之后进行刚度强度分析，实现了CAD 和CAE分析一体化。杨磊等[9]提出了一种基于横截面形状的参数化网格变形方法，以改变薄壁梁构件塑性铰区域的横截面形状，可快速获取局部变形的有限元模型，并采用代理模型技术和多目标遗传算法优化结构耐撞性。李亦文等[10]系统性研究了薄壁梁的弯曲机理，提出了一种改进的弯曲特性研究方法，可以省去繁琐的有限元分析过程，求出薄壁梁的弯曲特性曲线，提升了车身概念设计工作效率。潘星辰等[11]提出一种参数化的简化接头模型，由球铰单元与扭转弹簧单元构成，其弹簧刚度由详细模型解耦计算得到，通过实验研究发现，具有接头单元的概念车身模型的刚度更接近详细车身模型。

针对概念车身基于耐撞性的设计问题，本文以Kecman提出的理论模型为基础，引入塑性铰模型，尝试建立一种适用于概念设计阶段研究正碰耐撞性的框架车身，并在同等条件下与详细车身模型对比分析，最后对框架车身模型进行基于碰撞问题的梁截面优化。结果表明，本文方法建立的框架车身模型能较好满足概念设计的要求，并且能基于碰撞问题做梁截面优化分析，对车身的正向设计有积极意义。

2 塑性铰理论简介

薄壁直梁在弯曲载荷的作用下，当达到溃缩强度时，已无法再承受其他载荷，同时在局部产生褶皱变形，并且抗弯能力大幅下降。由于塑性变形集中在一部分条状区域，称这样一组塑形铰线构成一个塑性铰(plastic hinge)。一般现代的乘用车车身骨架结构由薄壁梁组成，发生碰撞时，大部分能量都由塑性铰吸收。Kecman[12]最先针对这种问题提出了一种理论模型近似描述薄壁梁的溃缩机理，黄贵龙[13]在此基础上，用能量法将截面参数和弯曲载荷下的弯矩与转角关系曲线建立了联系，为预测薄壁梁的弯曲特性和建立简化模型提供了条件。

利用能量法研究薄壁梁弯曲特性时，首先根据塑形铰线在变形过程中长度是否改变分为固定铰线和滚动铰线，如图1所示。

(1) 固定铰线：GH，EF，AC，KN，LM，GK，EL和KL。

(2) 滚动铰线：GA，EA，KA和LA。

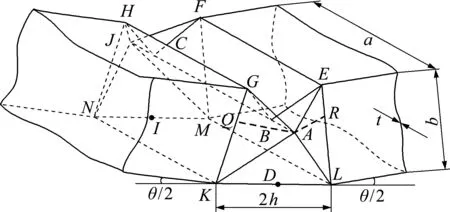
图1 Kecman理论模型[10]

Fig.1 Kecman theoretical model[10]

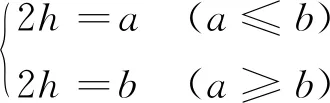
(1)

式中 固定铰线GH和EF处吸收的能量为

(2)

式中M0为单位长度塑性极限弯矩

M0=σ0(t2/4)

(3)

固定铰线BC处吸收的能量为

(4)

固定铰线AB和CJ处吸收的能量为

(5)

式中

(6)

固定铰线BG，BE，CH和CF处吸收的能量为

W4=WB G + B E + C H + C F=2M0hπ

(7)

固定铰线GK,EL,HN和FM处吸收的能量为

W5=WG K + E L + H N + F M=4M0barcsin

(8)

固定铰线KN和LM处吸收的能量为

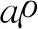
(9)

固定铰线KL和MN处吸收的能量为

W7=WK L + M N=4M0harctan(zA/yA)

(10)

式中

(11)

理论模型固定铰线处吸收的总能量为

(12)

滚动半径r取经验值

r=r(θ)=(0.07-θ/70)h

(13)

滚动铰线GA，AE，JH和JF处吸收的能量为

(14)

滚动铰线KA，LA，JN和JM处吸收的能量为

(15)

理论模型滚动铰线处吸收的总能量为

Wr=W8+W9

(16)

故薄壁梁弯曲塑性铰理论在模拟弯曲的过程中吸收的总能量为

(17)

则弯矩与转角的关系为

(18)

可见，仅需提供箱型梁截面的基本参数，即可得到该梁的弯曲刚度曲线方程，见式(18)。

3 框架车身模型建立

汽车正向设计中，在概念设计阶段，车身的设计细节尚未确定，为了快速得到车身梁截面的基本参数及车身的总体性能，常采用力学等效模型进行研究分析。本文采用梁壳混合的简化模型[14]，采用底板等大面积的板件结构，忽略非关键的细节特征，采用平坦的壳单元模拟，如图2所示。

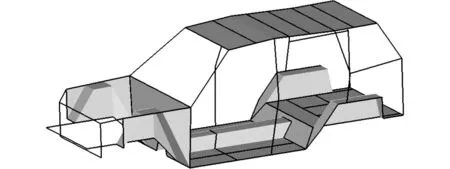
图2 简化模型

Fig.2 Simplified model

车身梁结构采用1D梁单元模拟，由于碰撞问题主要考虑梁结构的溃缩吸能，而截面的具体形状影响较小，故截面选用矩形截面，如图3所示。

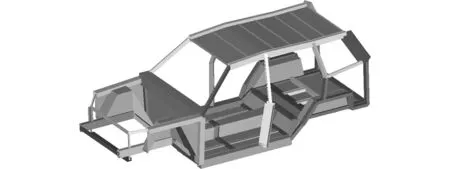
图3 简化模型(梁单元渲染)

Fig.3 Simplified model (beam rendered)

在碰撞仿真中，梁单元溃缩变形主要通过定义刚度特性曲线来描述。本文选用Belytschko -Schwer梁单元公式，LS -DYNA 中提供了一种专用于此公式的MAT29号材料[15]允许通过在点n1和n2 处定义三个方向的弯曲特性来模拟塑形铰，图4 为该梁单元示意图。梁单元之间通过共节点方式连接，且可以通过节点传递力和力矩。与传统的建模方式相比，省去了梁单元之间建立弹簧连接这一繁琐的过程，提高了建模效率，且在研究碰撞这种复杂的问题时，避免了很多不必要的问题出现，显著节省时间。

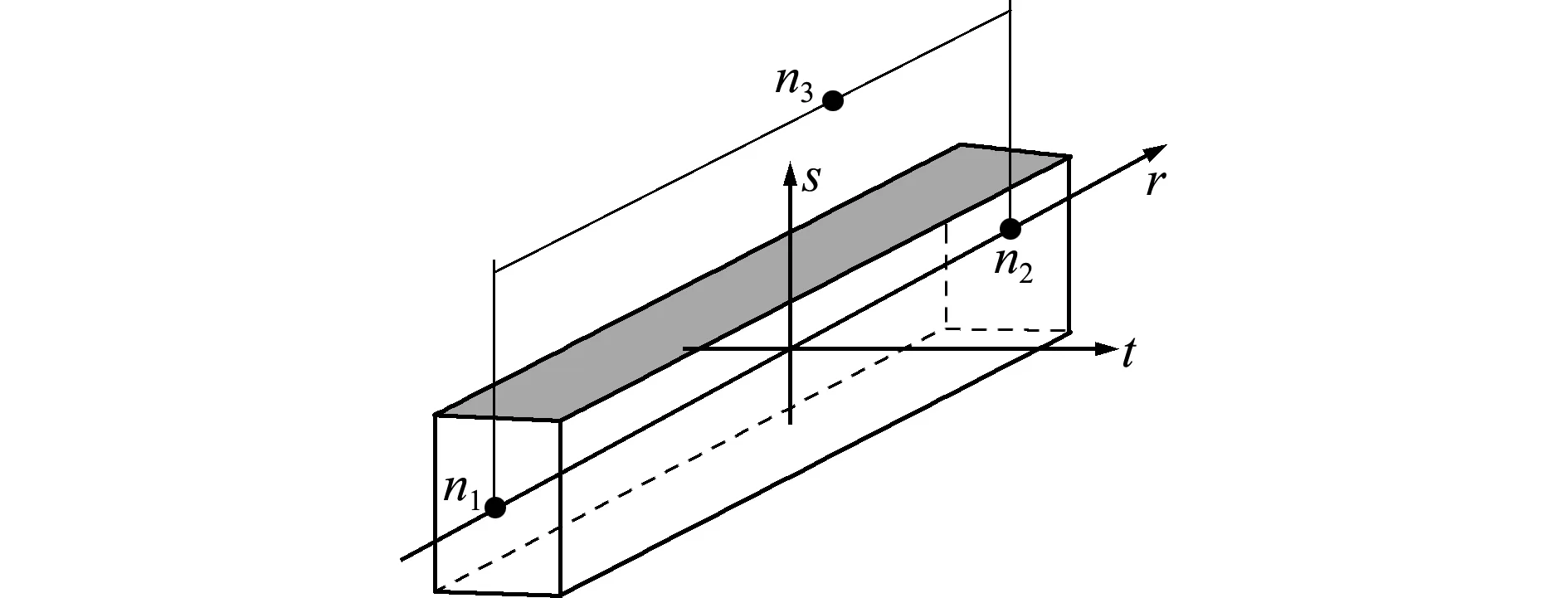
图4 Belytschko -Schwer梁单元

Fig.4 Belytschko -Schwer beam element

传统的刚度特性曲线由详细梁模型计算得到，而在正向设计中没有具体的梁截面参数，这种方法没有意义。若将梁截面简化为薄壁矩形，就可应用前文所述的方法计算得出刚度曲线，即能在正向设计的简化模型中定义塑性铰。

为验证计算方法定义塑性铰的可靠性，建立了如图5所示V-型梁模型，进行详细模型与简化模型的对比分析。

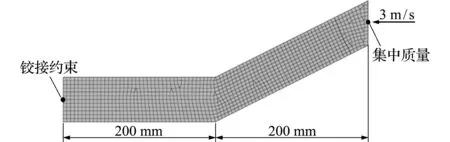
图5 V-型梁详细模型

Fig.5 Detailed model of V-beam

在V-型梁右侧截面设置水平向左3 m/s的初速度，拐角处设置一截面以测量该处弯曲与转角的关系曲线。同时根据式(18)，代入截面的基本参数，计算得到刚度曲线。两种模型得到的曲线对比如图6所示。可以看出，详细模型得到的刚度曲线与简化模型有限元分析得到的结果相比，误差较小，满足概念设计的要求。

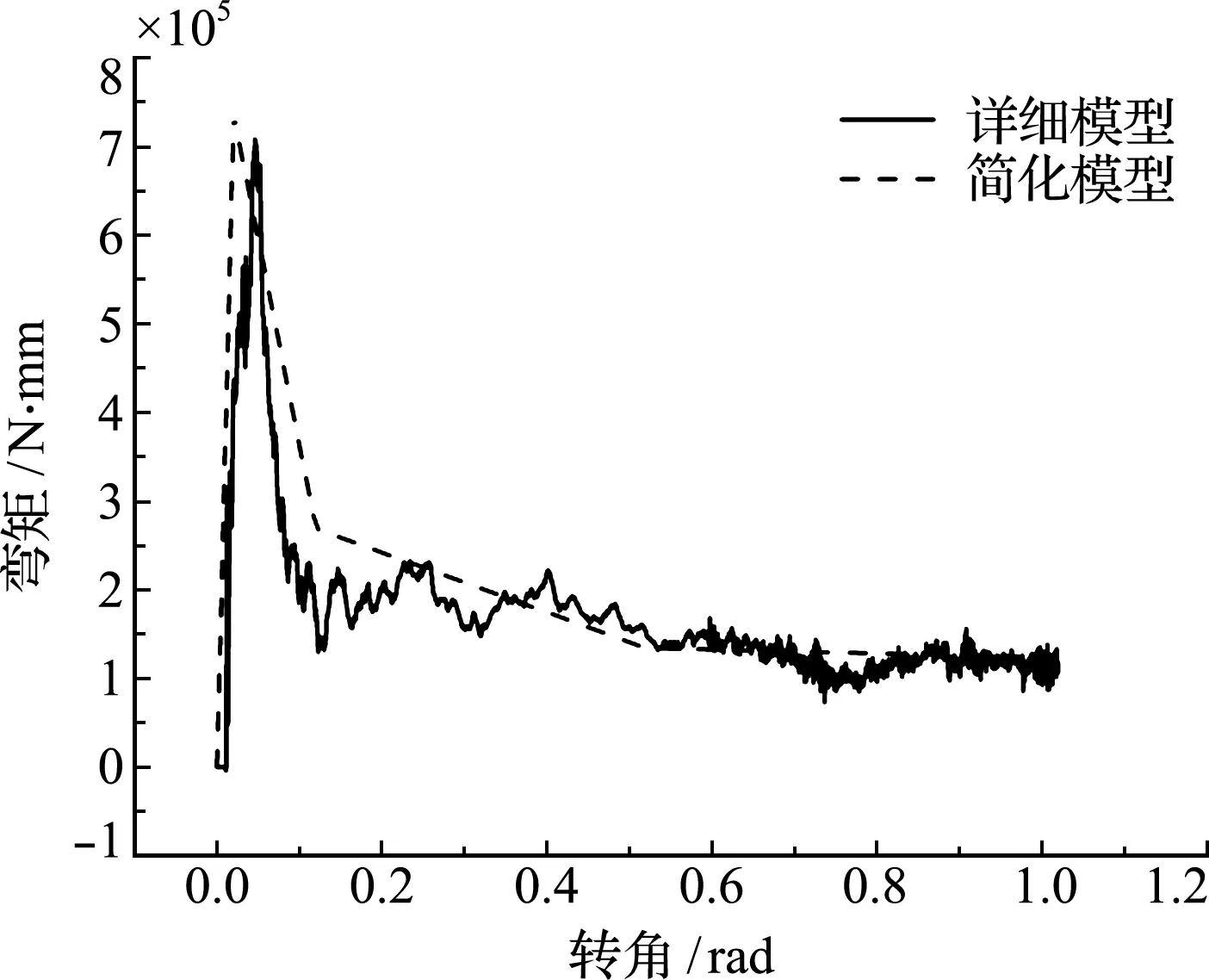
图6 简化模型与详细模型的刚度曲线对比

Fig.6 Comparison of the stiffness curves between theoretical model and detailed model

将理论计算得到的刚度曲线赋予简化的V-型梁拐点处，梁单元节点处即定义了塑性铰。所有外部约束条件均设置为与详细模型相同。两种模型的变形如图7所示。变形过程内能变化对比如 图8 所示。

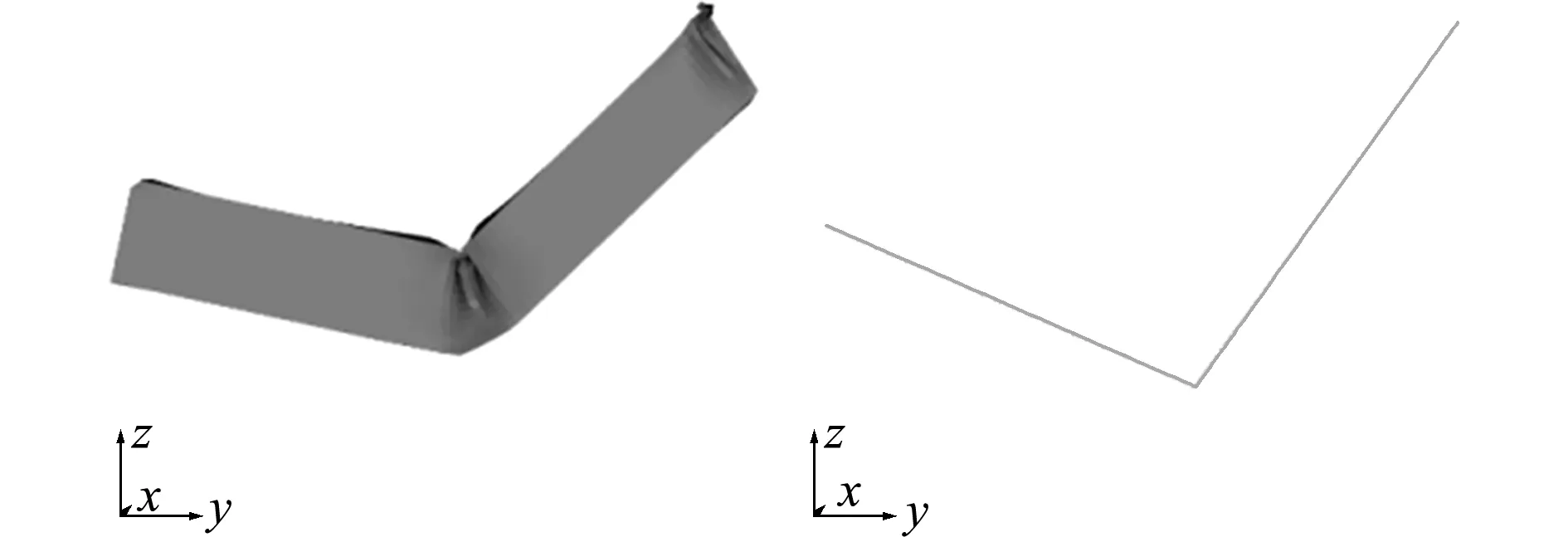
图7 V-型梁变形对比

Fig.7 Comparison of V-beam deformation

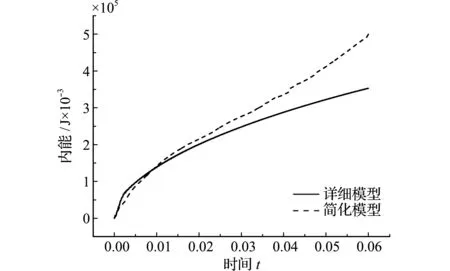
图8 V-型梁内能对比

Fig.8 Comparison of internal energy of V-beam

从变形图和形变过程内能变化对比可以看出，式(18)得到的刚度曲线，以及通过梁单元节点处定义塑性铰的方法，可以在一定程度上描述详细梁结构低速运动的过程。

4 车身碰撞对比分析

4.1 正碰仿真

将前文所述的塑性铰赋予框架车身中前纵梁等吸能构件，具体为将梁的刚度特性曲线添加到对应的材料卡片中，即成为可用于碰撞分析的车身模型，如图9所示。同时在详细模型中设置相同的工况，在车身正前方放置固定的刚性墙，整车赋予 16 km/h 的初速度，分析时间设为100 ms，进行碰撞分析。

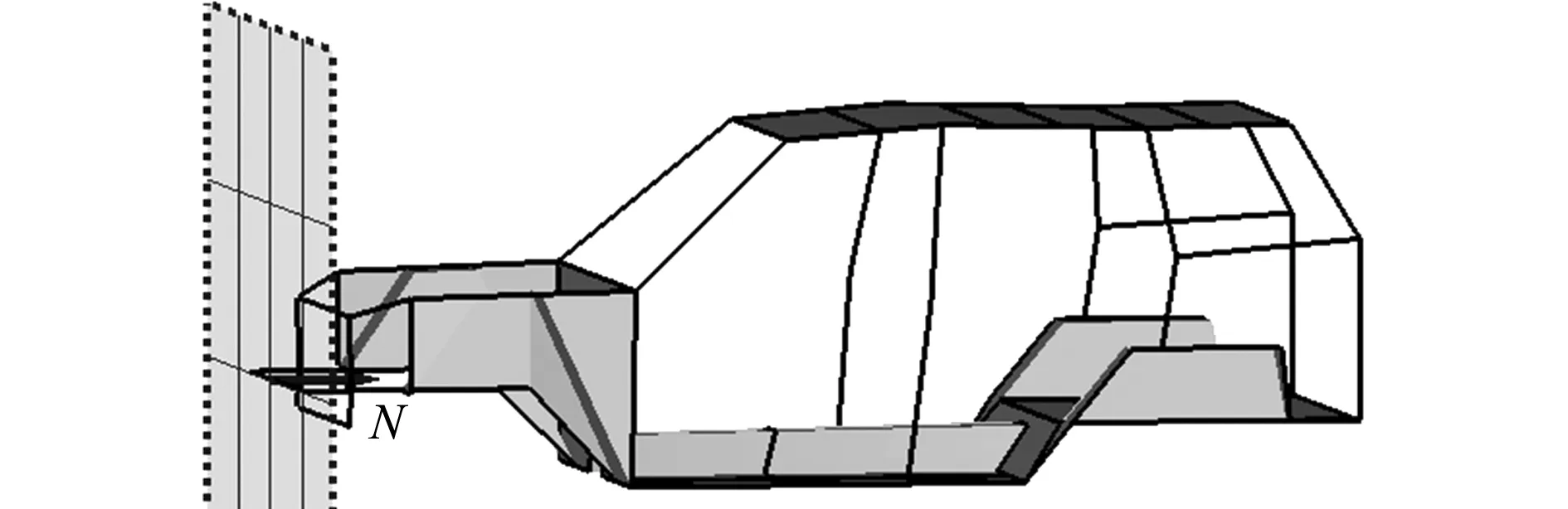
图9 车身碰撞分析模型

Fig.9 Collision analysis body model

(1) 总体数据对比

由表1可知，详细模型和简化模型的初始条件相同，这就保证了有限元分析对比的可行性。由于最大碰撞力是碰撞分析中的一个重要指标，反映了乘员在碰撞发生时受到的伤害，所以有限元分析输出碰撞峰值力作为对比项。由表2可知，简化模型的碰撞反力较低，误差达到了32.93%，但作为概念设计阶段对碰撞的预测考虑，此误差满足要求。最重要的是，简化模型的分析时间较详细模型大幅降低，仅有其0.4%，这也为后续的优化工作提升了效率。所以简化模型的分析是十分有意义的。

(2) 碰撞各时刻变形对比

详细模型和简化模型在碰撞分析中各时刻的对比如图10所示。可以看出，简化模型模拟了车身在碰撞过程中前纵梁和前围结构的弯曲和溃缩现象，各时刻的变形特征基本吻合，这就为概念设计阶段的车身前端吸能结构的分析提供了条件。两者相比，详细模型的溃缩现象更为明显，简化模型的主要变形形式则是弯曲。两者在防火板之后的变形可以忽略。

表2 计算结果

Tab.2 Calculation results

计算时间最大碰撞反力/kN详细模型1h38min58s441.334简化模型24s295.987误差/%—32.93效率/%99.60—注:误差和效率均以详细模型数据为基准。

图10 各时刻变形(侧视)

Fig.10 Deformation at each moment (side view)

(3) 能量对比

详细模型和简化模型的能量曲线如图11和图12所示。可以看出，详细模型和简化模型都很好地满足了能量守恒定律，两者的总能量相同，且两者的沙漏能与界面能都小于总能量的5%，故仿真结果有效。不同之处在于，详细模型能量稳定的时间更晚，这主要是因为详细模型车身前端的复杂吸能结构起到了缓冲的作用。

4.2 误差分析

(1) 在简化建模过程中，省去了许多次要结构，使得初始模型存在误差。

(2) 详细模型的梁结构压溃现象更明显，而简化模型的梁单元主要在节点处发生弯曲，这是受仿真软件中梁单元模型本构关系的影响造成的。

(3) 刚度特性曲线是很复杂的曲线，受计算或提取方法的制约，不能完全真实反映实际的变形情况。且在赋予到简化模型中时，也对曲线进行了一定的简化。

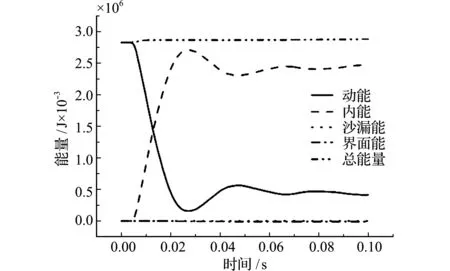
图11 详细模型能量曲线

Fig.11 Energy curves of detailed model

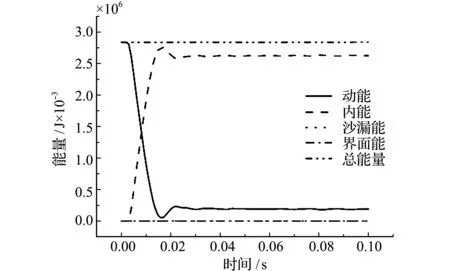
图12 简化模型能量曲线

Fig.12 Energy curves of simplified model

(4) 塑性铰定义在梁单元节点连接位置，故梁单元网格尺寸会影响到塑性铰的数量。

(5) 在简化模型中，塑性铰定义在车身前脸的纵梁处，而详细模型的车身前脸如保险杠等横梁也出现了压溃变形，吸收了部分能量。由于梁单元无法定义径向压溃，故不能模拟这部分变形。

从正碰仿真分析可以看出，简化模型在一些正撞问题的关键指标中能较好地描述详细模型的变形过程，能为概念设计阶段提供正碰情况的预测，为设计工作者提供参考依据。且计算时间大幅减少，提升了设计工作效率。此外，简化模型梁单元的截面参数较少，易于进行优化设计。

5 框架车身耐撞性优化

5.1 优化问题描述

为了满足轻量化的设计要求，优化将车身总质量作为目标函数。在发生碰撞时，最大碰撞力反映了冲击力对成员的影响，这是汽车设计中非常重要的一项指标，故在优化中将车身与刚性墙碰撞的峰值力FMax作为约束条件。框架车身的梁截面均为薄壁矩形截面，设计变量为矩形截面的边长w和h，以及厚度t三个参数。同时，为了保证截面优化不出现无效解，将截面的三个参数值约束在以初始值为基准的一定区间内。这样就把设计变量和目标函数质量M建立了联系，且刚度特性曲线可以由梁截面参数计算得出，在优化迭代过程中，刚度特性曲线可以随梁截面参数变化更新。于是，优化问题可以定义为

优化方法采用移动渐近线法MMA(Method of Moving Asymptotes)，该方法为基于一阶Taylor展开式的凸近似方法，近似函数用原函数在当前设计点处的一阶导数来表示。MMA方法通过引入移动渐近线，将隐式的优化问题转化成一系列显式可分离的严格凸近似子优化问题。每一步迭代中，通过用梯度类算法求解凸近似子问题来更新设计变量。优化流程如图13所示。

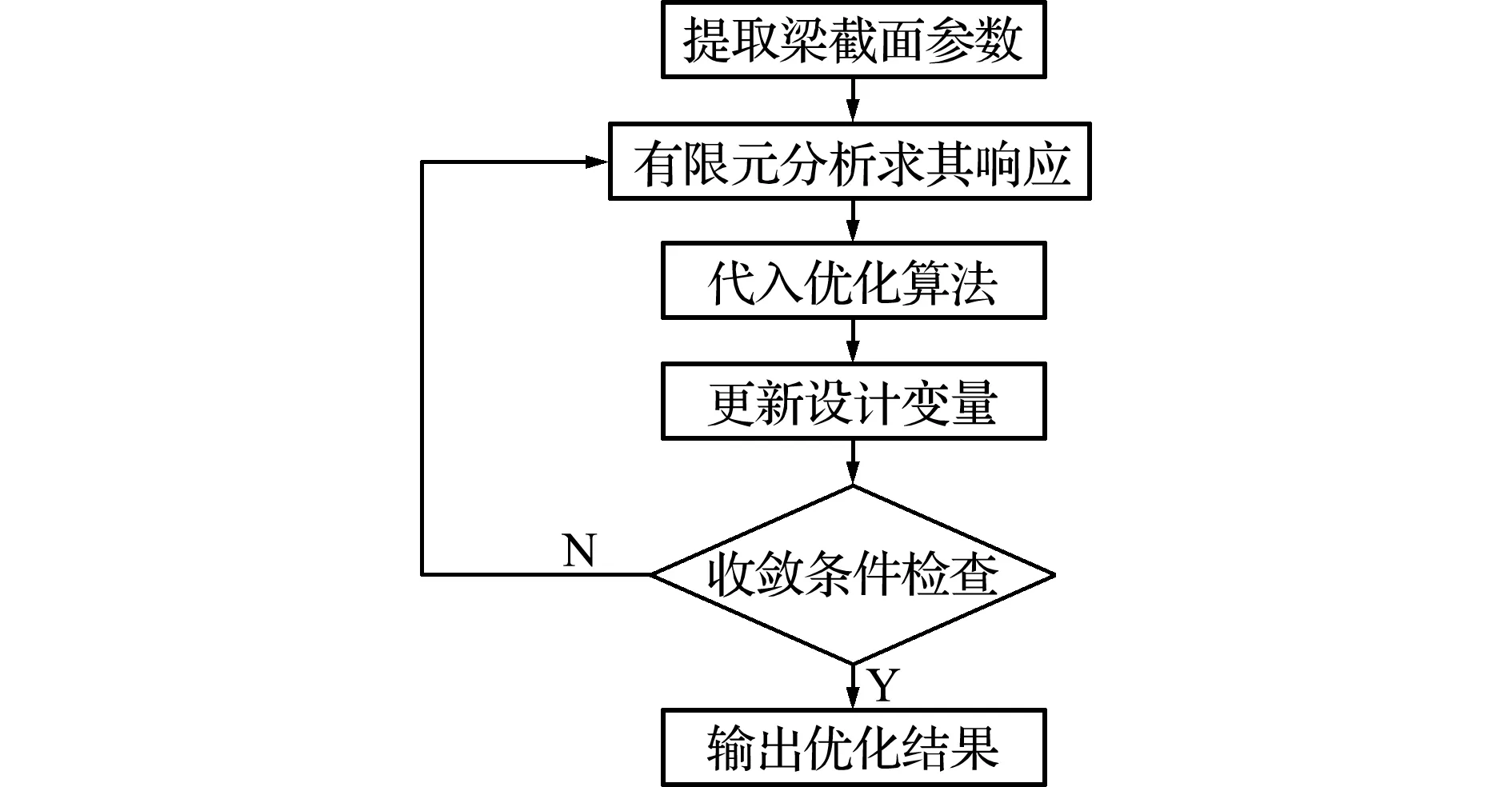
图13 框架车身耐撞性优化流程

Tab.13 Optimization process of frame body crashworthiness

5.2 优化结果

应用MMA算法对上述问题进行优化，经 20次 迭代后，目标函数收敛，如图14所示。

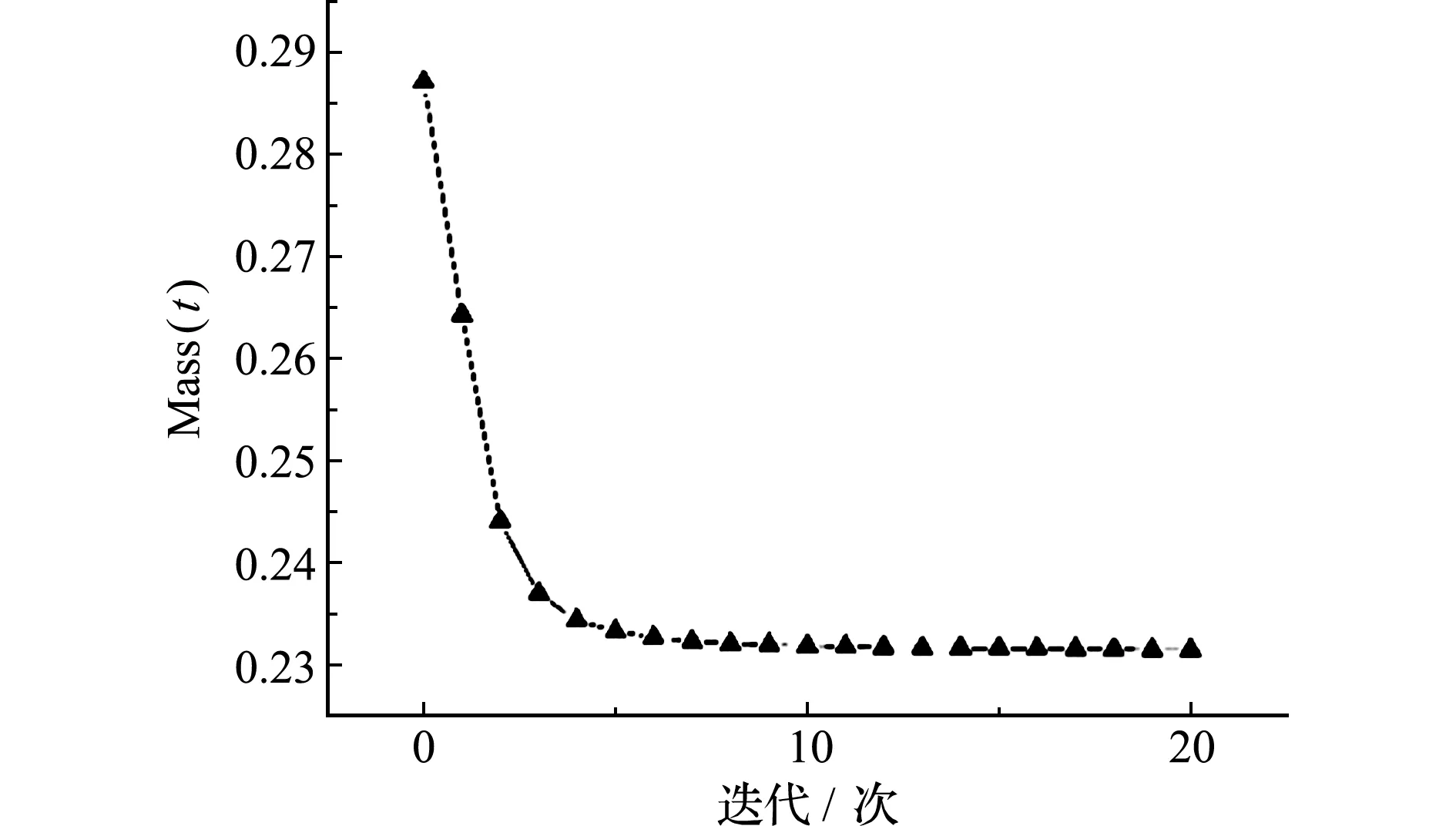
图14 目标函数收敛情况

Fig.14 Target function variation diagram

优化完成后，车身的总质量M=231 kg，与初始值相比，减重为19.60%，减重效果较为明显。最大碰撞力优化前后的对比如图15所示。可以看出，最大碰撞力均保持在规定的范围内，且优化后的碰撞力有所降低，主要原因是整车质量减少。

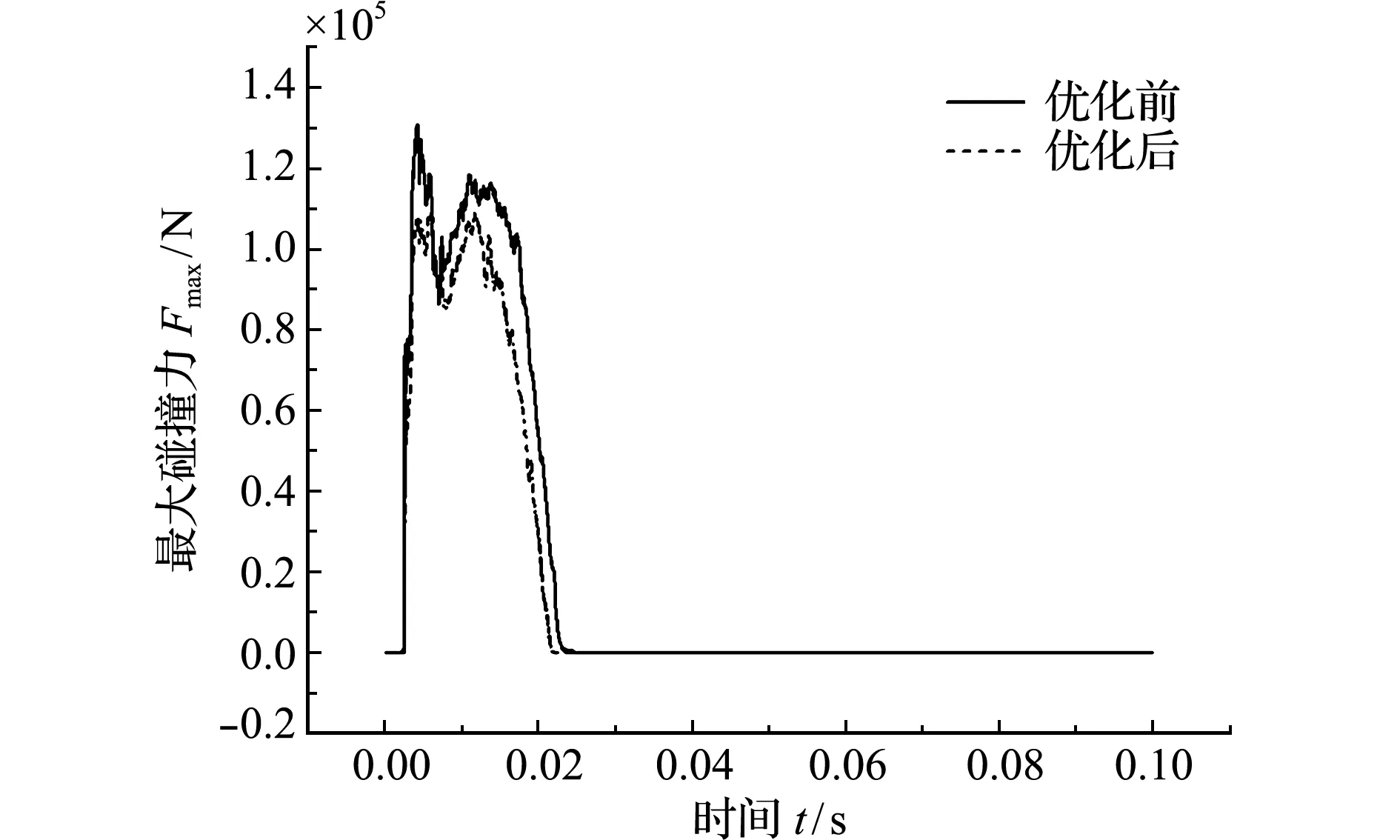
图15 最大碰撞力优化前后对比

Fig.15 Comparison before and after optimization of maximum collision force

梁截面优化前后的截面设计变量变化列入 表3。表3的梁截面数据可为设计者提供详细阶段的参考，进行形状优化等后续设计。优化过程总计运行12 h，对于车身模型而言，优化时间较快，提升了概念设计阶段的设计工作效率。

表3 优化前后梁截面设计变量

Tab.3 Comparison of beam section data before and after optimization

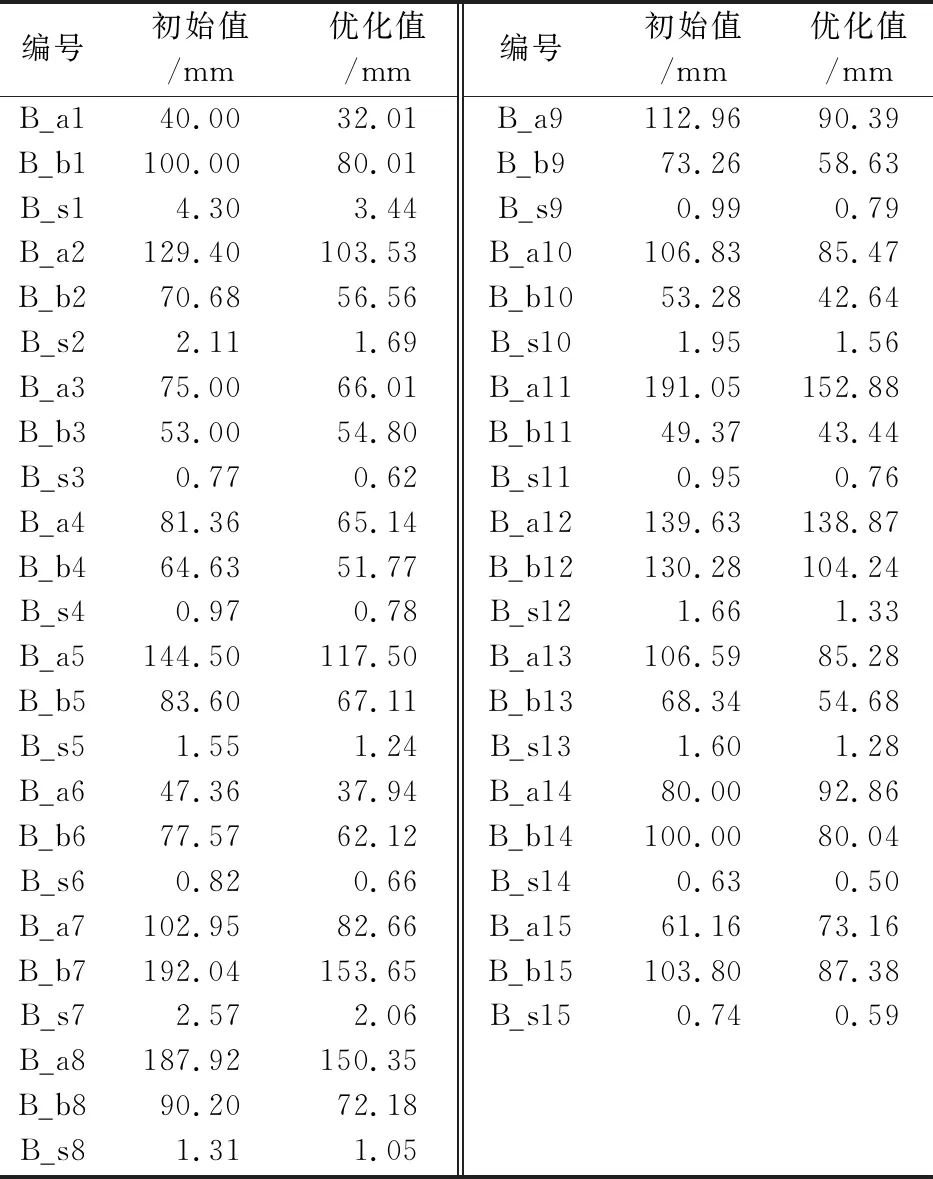
编号初始值/mm优化值/mmB_a140.0032.01B_b1100.0080.01B_s14.303.44B_a2129.40103.53B_b270.6856.56B_s22.111.69B_a375.0066.01B_b353.0054.80B_s30.770.62B_a481.3665.14B_b464.6351.77B_s40.970.78B_a5144.50117.50B_b583.6067.11B_s51.551.24B_a647.3637.94B_b677.5762.12B_s60.820.66B_a7102.9582.66B_b7192.04153.65B_s72.572.06B_a8187.92150.35B_b890.2072.18B_s81.311.05编号初始值/mm优化值/mmB_a9112.9690.39B_b973.2658.63B_s90.990.79B_a10106.8385.47B_b1053.2842.64B_s101.951.56B_a11191.05152.88B_b1149.3743.44B_s110.950.76B_a12139.63138.87B_b12130.28104.24B_s121.661.33B_a13106.5985.28B_b1368.3454.68B_s131.601.28B_a1480.0092.86B_b14100.0080.04B_s140.630.50B_a1561.1673.16B_b15103.8087.38B_s150.740.59

6 结 论

本文使用梁壳混合的模型搭建框架车身，在梁单元节点处赋予弯曲刚度曲线以模拟塑性铰，并赋予其用Kecman理论模型方法计算得到的刚度曲线，之后对框架车身模型进行正碰仿真，与详细车身模型比较，有较高的精度，验证了框架车身的可靠性，同时计算时间仅为详细模型的0.4%，在精度和效率上满足概念设计阶段的要求。在此基础上，进行了框架车身的耐撞性优化设计，车身轻量化效果较为明显，解决了传统概念框架车身不能基于碰撞优化的问题。得到的梁截面数据可为设计者后续工作提供参考。本文方法可应用于汽车结构概念设计阶段的优化设计工作，尤其是在概念设计阶段即考虑了碰撞的影响，对汽车制造企业缩短研发周期，提高设计工作效率有积极意义。