双层石墨烯系统稳态受迫振动问题中的辛方法

范俊海，贾菊芳，赖安迪，周震寰，徐新生

(大连理工大学 工程力学系 工业装备结构分析国家重点实验室，大连116024)

1 引 言

随着科学技术的进步，设备和器件向轻型化和微型化发展，石墨烯和纳米结构得到广泛应用[1]。如纳米转子、光子晶体悬臂传感器和扫描探针原子力学显微镜等[2]。纳米结构作为纳米器件中的关键部件，往往起到不可或缺的作用。石墨烯作为一种纳米结构，其动力响应直接影响到纳米器件的性能，因此对其进行研究是十分必要的。

在小尺度效应下，经典弹性理论已经不能表述纳米结构的问题,因此提出一些新的理论方法来分析纳米结构。Eringen[3]的非局部理论作为一种连续弹性理论已经应用于纳米结构静力学和动力学的分析。基于Navier解法，可以得到镶嵌在粘弹性介质中的单层简支石墨烯受迫振动问题的解析表达式[4]。Navier解法也可以求解板内磁场作用下，简支双层正交各向异性纳米板的受迫振动问题[5]。Navier解法在解决热环境下正交各向异性简支纳米板在移动载荷作用下的动力响应问题时也是有效的[6]，但是局限在解决简支纳米板的动力问题。由于悬臂纳米板振动问题边界条件的特殊性，目前还没有有效的方法进行解析求解。辛方法[7,8]对于非简支板问题有一定的优势[9,10]，可将问题归结为辛本征解展开。在特殊的非简支板动力问题中，采用哈密顿体系的方法可以得到受迫的解析解[11]。本文针对多层悬臂石墨烯系统，采用非局部弹性理论和哈密顿体系相结合的方法以及子问题分解方法，研究了其受迫振动问题的动力特性，并提出一种有效的方法。

2 基本问题

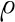
采用非局部理论和正交各向异性板模型，引入线性微分算子L=1-ξ22，式中ξ2为微观非局部参数，2为Laplacian算子。在频域下每一层板的控制方程可以写成统一形式：

图1 基本模型

Fig.1 The model

L(pww+pw′w′+q)=0

(1)

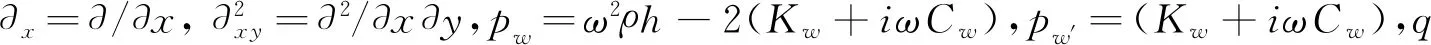
3 边界条件及分解

根据基本模型，两石墨烯板均为悬臂支承，即一边为固支条件(以字母C表示)，另三边为自由边界条件(以字母F表示)，在数学上边界条件[15]表示为

Vx|x = 0=0,Mx|x = 0=0,w|x = a=0

θx|x = a=0,Vy|y = 0,b=0,My|y = 0,b=0

(2)

Vx|x = 0=Vy|y = 0,b=w|x = a=θy|y = 0,b=0

(3)

Vx|x = 0=Vy|y = 0,b=w|x = a=θx|x = 0=Mx|x = a=0

(4)

Vx|x = 0=θx|x = 0=w|x = a=Mx|x = a=Vy|y = 0,b=

θy|y = 0,b=0

(5)

(6)

这样就可以将一个边值问题分解为三个容易求解的边值问题。

4 哈密顿系统表示方法

(7)

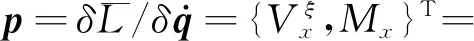
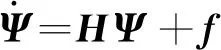
(8)

(9)

在式(8，9)中，f={0,0,-Lq,0}T。对正则方程(8,9)求解，并让其解满足边界条件，即可得到问题的解。

5 哈密顿体系正则方程的求解方法

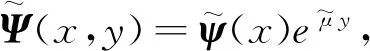
Ψ=[A1a1sinh(λ1y)+A2a1cosh(λ1y)+

A3a2sinh(λ2y)+A4a2cosh(λ2y)]eμ x

(10)

(11)

(12)

式中J为辛单位矩阵[7]，分别存在辛共轭正交关系：

(13)

其他情况全为0。其中α类指本征值实部大于0，或实部等于0且虚部大于0；β类为负的α类本征值。

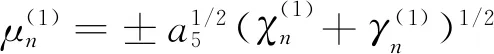
(14)

《著作权法》规定对著作权构成侵犯的以及侵犯著作权的相关权利的，按照实际情况进行赔偿。对于难以计算损失数据的，根据侵权人的违法所得进行赔偿。赔偿数额包括为阻止侵权行为的一切合理合法支出。对损失难以计算或者违法所得不确定的情况，应当按照实际情况，处50万元以下的罚款。总之，侵权数额的赔偿要根据实际损失情况、违法所得的金额进行确定，具体情况具体分析。

(15)

(16)

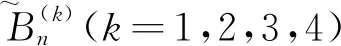
(17)

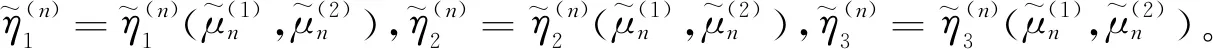
注意第三种边界条件(5)和非齐次方程(8,9)，满足部分边界条件的(8,9)齐次方程通解(14,16)仍成立。非齐次方程(8,9)的特解可通过辛共轭正交关系[7]分别得到。该问题的解由齐次方程通解和非齐次方程特解叠加而成，即

(18)

(19)

(20)

6 双石墨烯板受迫振动问题

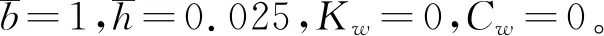
表1 固有频率对比

Tab.1 Comparisons of natural frequencies

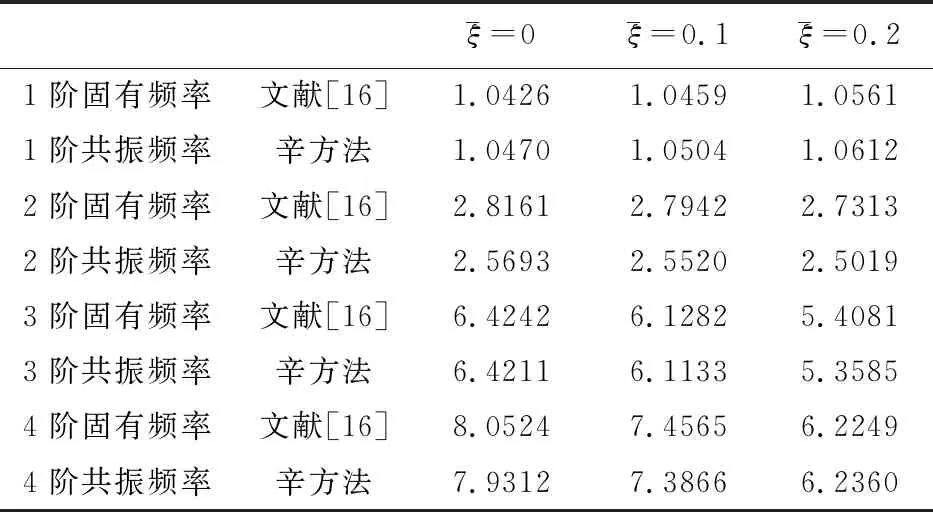
ξ=0ξ=0.1ξ=0.21阶固有频率文献[16]1.04261.04591.05611阶共振频率辛方法1.04701.05041.06122阶固有频率文献[16]2.81612.79422.73132阶共振频率辛方法2.56932.55202.50193阶固有频率文献[16]6.42426.12825.40813阶共振频率辛方法6.42116.11335.35854阶固有频率文献[16]8.05247.45656.22494阶共振频率辛方法7.93127.38666.2360

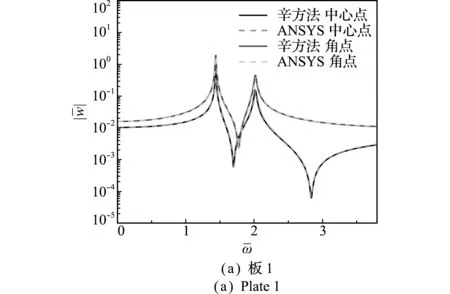
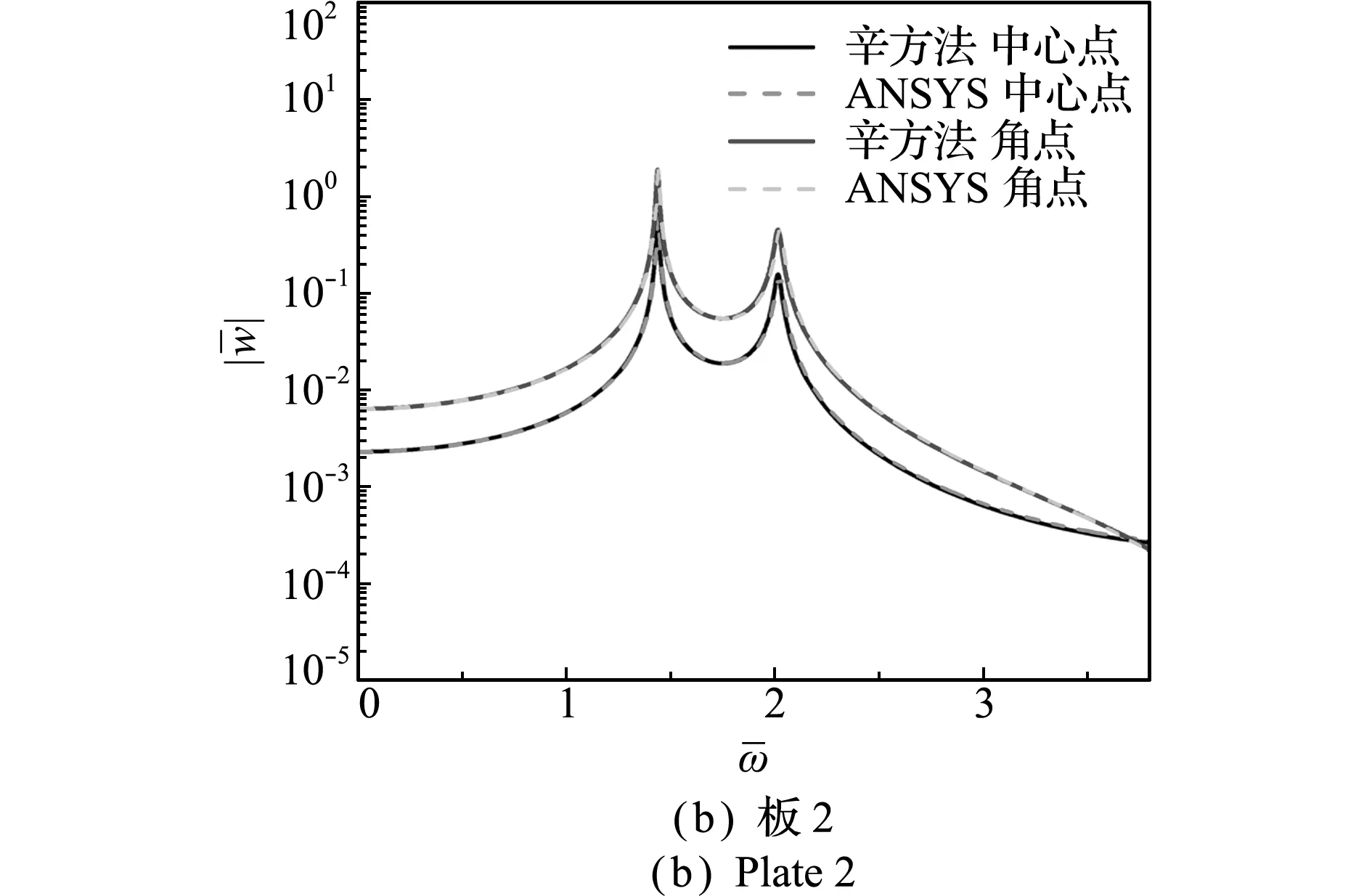
图2 悬臂双层正交各向异性矩形板频响曲线

Fig.2 Frequency-response curve of double -layered cantilever orthotropic rectangular plates

图3 单层与双层石墨烯板频响曲线

Fig.3 Frequency-response of single -layered and double -layered

图5给出了弹性模量比E2/E1和剪切模量比G12/E1对受迫振动的影响，仍选取算例1的参数和外载，计算了在E2/E1=0.5,1.0,1.5,2.0和G12/E1=0.2,0.3,0.4,0.5时板1载荷点的频响曲线。可以看出,E2/E1和G12/E1对第1阶和第2阶共振频率几乎无影响，主要是因为主体弯曲变形是沿x方向所致；但其对高阶共振频率的影响随E2/E1和G12/E1的增加，变化越来越大。事实上，由于两个方向上强度的变化会直接影响固有频率的大小，从而也会改变振动模态所对应固有频率的顺序。

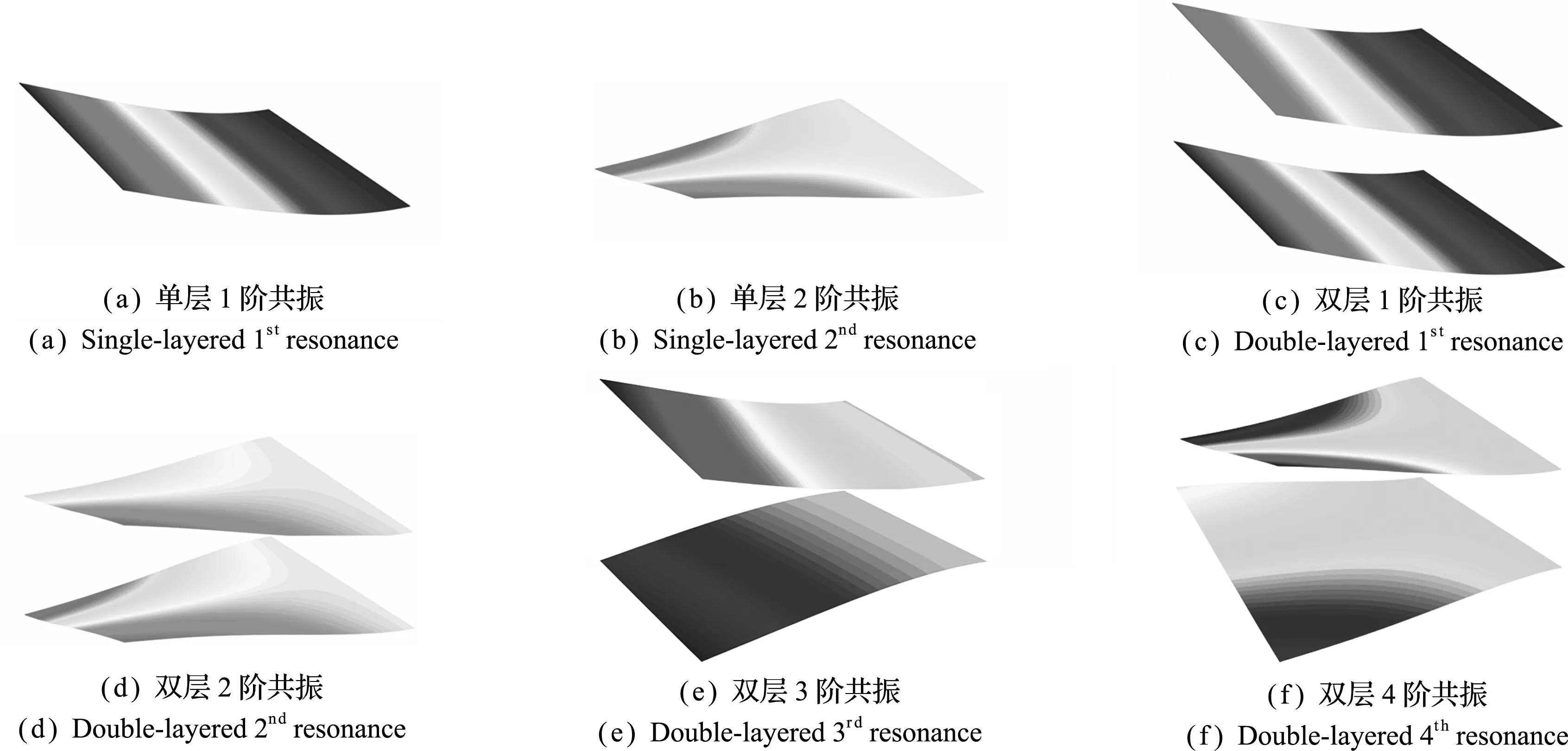
图4 单层和双层石墨烯板系统共振模式响应

Fig.4 Response modes of single -layered nanoplate and double -layered graphene plates

图5 弹性模量比和剪切模量对频响曲线的影响

Fig.5 Frequency-response with different elastic modulus ratio and shear modulus

7 结 论

Eringen非局部理论与哈密顿体系相结合可以表述多层石墨烯受迫振动问题。通过边界条件分解技术和变量组合方法，可以得到由辛本征值和辛本征解表示的双层石墨烯层板受迫振动问题的解析解表达式，对悬臂石墨烯系统特别有效，且辛本征解级数方法具有很好的收敛性和精度。结果表明，弹性模量和剪切模量对高阶共振频率影响较大；双层石墨烯受迫振动的特点在于可发生同向振动模式和反向振动模式。