一种质量块-弹簧自参数共振压电俘能器研究

2020-10-28陈忠成解小东

压电与声光 2020年5期

陈忠成，解小东，谢进

(西南交通大学机械工程学院，四川成都 610031)

0 引言

近年来，收集环境振动能量为微电子设备提供电能的俘能器研究越来越多[1-3]。其中，压电俘能器因其结构简单、能量密度高而备受关注[4-5]。

目前多数压电俘能器是以直接激励方式工作。但有研究表明，参数激励比直接激励更能产生高的响应幅值[6]。Daqaq等[7]建立了参数激励压电俘能器的集中参数模型，并在该模型中考虑了几何非线性和惯性非线性。Abdelkef等[8]建立了参数激励压电俘能器的分布参数模型。Lan等[9]研究了带末端质量块的参数激励俘能器的内共振特性。

参数激励压电俘能器存在的主要问题是激励阈值高及工作带宽窄。为了克服存在的问题， Jia等[10-12]通过引入一个两端固支的水平梁作为直接激励，提出了一种自参数共振的参数激励俘能器，实验证明，与传统俘能器相比，该俘能器激励阈值低，工作带宽宽。Yan等[13-14]推导了自参数共振参数激励俘能器的理论模型，进一步揭示了其工作特性及其原理。Yang等[15]引入了一个水平梁，通过直接激励的水平梁和参数激励的竖直梁间的磁耦合来实现降低激励阈值及提高工作带宽的功能。这些新型的自参数共振参数激励压电俘能器的结构设计均增加一个水平梁作为直接激励，以此对激励起放大作用，进而降低了参数的激励阈值，提高俘能带宽。实际上，水平梁的增加是为系统增加了一个新的自由度，但加大了俘能器的结构尺寸。

本文借鉴自参数共振的参数激励压电俘能器增加一个自由度以降低激励阈值及增加俘能带宽的思路，提出在压电梁末端增加质量块-弹簧的二自由度参数激励俘能器，并对该俘能器发生参数共振时的激励阈值与俘能带宽进行分析和讨论。

1 质量块-弹簧压电俘能器的结构及数学模型

1.1 质量块-弹簧压电俘能器的结构及其动力学方程

本文提出的质量块-弹簧压电俘能器的结构如图1所示。该俘能器在参数激励俘能器压电梁的末端加装一个弹簧和质量块。当俘能器受到外界沿z方向上的振动激励时，压电梁在末端质量块及弹簧的共同作用下发生参数共振。图中，h为弹簧的高度，m0为末端质量块质量，l1为压电片距离地面的距离，ls为梁长度，bs为梁的宽度，hs为梁的厚度，lp为压电片长度，bp为压电片宽度，hp为压电片厚度，z(t)为外界激励位移。

图1 质量块-弹簧压电俘能器的结构

图1所示结构与现有的一些参数激励俘能器的主要区别是：本文提出的结构是在质量块与压电梁之间增加一个弹簧，相当于系统增加了一个自由度。本文假设压电梁末端的滑动平台的质量和弹簧质量都很小，可忽略不计，且弹簧为线性弹簧。

采用扩展哈密顿原理推导出俘能器的机电耦合数学模型。扩展哈密顿原理的表达式为

(1)

式中：q为压电梁的广义位移;s为末端质量块相对于压电梁末端的广义位移;V为压电片的电压;t为运动时间;L=T-U-W为拉格朗日函数,T为系统的动能,U为系统的势能;W为压电片电势能；δw为非保守力所做虚功的变分，且:

(2)

俘能器的动能为压电梁的动能和末端质量块的动能之和，即:

(3)

当梁足够细长，假设梁不可伸展，梁的横向位移和轴向位移间的关系为

(4)

俘能器的机械势能包括梁应变的势能、梁的重力势能、末端质量块的重力势能及弹性势能，则总机械势能为

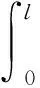
z(t)]dx+m0g[s(t)+z(t)+u(l,t)]+

(5)

式中：(′)为对位移求导;k为弹簧的刚度;s(t)为末端质量块与压电梁末端的间距;u(l,t)为压电梁末端与地面的轴向间距;z(t)为地面上下振动位移;EI为梁抗弯刚度。

压电片电势能为

(6)

式中：θp为压电片的机电耦合系数；Cp为压电片的压电电容。

为了得到系统的离散模型，假设一阶振型占主导，压电梁的横向位移w(x,t)为

w(x,t)=φ(x)q(t)

(7)

式中：q(t)为只与时间相关的广义位移；φ(x)为该系统的模态函数。对于两端固支的边界条件，模态函数为

(8)

将式(3)、(5)、(6)代入式(1)可得到质量块-弹簧压电俘能器的机电耦合方程：

(9)

为了对比分析质量块-弹簧对压电俘能器俘能特性的影响，式(9)中令k=0，可得无弹簧的压电俘能器，即现有的一些压电俘能器的动力学方程为

(10)

1.2 质量块-弹簧压电俘能器的系统参数及动力学性能

本文中取压电俘能器的系统参数及几何尺寸如表1所示。表中，Es、Ep为杨氏模量,ρs、ρp为梁的密度，d31为压电常数，ε33为介电常数。

表1 压电俘能器的系统参数及几何尺寸

k2q+k4q3=0

(11)

当k2>0时，压电梁不屈曲，系统仅一个稳定平衡点(0,0)；当k2<0时，压电梁发生屈曲，此时系统有3个平衡点, 其中1个为不稳定平衡点(0,0)，另外两个为稳定平衡点，即

(12)

k2=0为压电梁屈曲与不屈曲的分界点，对应的末端临界质量用Mc表示。当m0

(13)

当m0>Mc时，压电梁的固有频率为

(14)

由表1中的系统参数和几何尺寸及式(12)～(14)可得到系统的平衡点和压电梁的f1随m0的变化规律，如图2所示。

图2 压电梁的平衡点和固有频率

由图2可知，Mc≈0.033 kg。当m0Mc时，系统有3个平衡点，其中2个为稳定平衡点，用实线表示，一个为不稳定平衡点，用虚线表示(见图2(a))；当m0Mc时，随着m0的增加f1增大(见图2(b))。

弹簧-质量块的固有频率为

(15)

当m0

2 质量块-弹簧压电俘能器俘能特性分析

根据文献[17],系统的输出功率与均方根电压(Vrms)的平方成正比。本文以Vrms作为俘能器的评价指标，则有：

(16)

本文主要研究压电梁在未发生屈曲时的自参数共振系统的俘能性能。根据1.2节的分析，选取m0=0.003 5 kg

本文采用数值分析法进行分析，在未特别说明的情况下，其仿真的初始值均取为0，R取为5 MΩ。

图3为有、无弹簧时Vrms和压电梁的位移随着激励幅值(A)变化的关系曲线。由图可知，无论是否有弹簧，该系统都存在一个激励阈值，只有A大于激励阈值时，压电梁才会发生参数共振。有弹簧时激励阈值为0.5 m/s2，无弹簧时激励阈值为4.2 m/s2。由此可知，在质量块与压电梁之间加装弹簧能够大幅降低俘能器的激励阈值。

图3 Vrms和位移随A变化的关系曲线

为了进一步分析质量块-弹簧的直接共振与梁的参数共振，取A=0.3 m/s2<0.5 m/s2，梁的初始位移取5 mm，作出质量块和压电梁时域图，如图4所示。

图4 A=0.3 m/s2时压电俘能器的时域图

由图4(a)可知，弹簧的振幅在1 s内先快速增大，然后又减小到一定值，这是因为弹簧将一部分能量传递给了压电梁。由图4 (b)可知，梁的振幅经历了缓慢减小的过程，由于有弹簧的作用，减小的速率较慢。

当A=1.2 m/s2>0.5 m/s2，梁的初始位移为5 mm，作出质量块和压电梁时域图，如图5所示。

图5 A=1.2 m/s2时压电俘能器的时域图

由图5可知，质量块-弹簧发生直接共振，而压电梁发生了参数共振。质量块-弹簧与压电梁之间能量转换过程为：刚开始激励时，弹簧首先发生直接共振，经过一段时间后，将能量传递给压电梁，促使压电梁发生参数共振，再经过一段时间，弹簧的位移减小为一定值。由此可知，压电梁的参数共振是外部激励和弹簧共同作用的结果。

当A=5 m/s2时，俘能器的Vrms对于不同Ω的频率响应如图6所示。

图6 A=5 m/s2时压电俘能器频率响应

由图6(a)可知，无弹簧时，俘能器的正、反向扫频有微小差别,俘能带宽为20.70 Hz-19.95 Hz =0.75 Hz，均方根电压峰值为1.2 V。由图6(b)可知，有弹簧的俘能器的正、反向扫频差异较明显，说明加装弹簧后系统表现出较强的软化和硬化相结合的特性，增强了参数共振，俘能带宽为22.4 Hz-17.4 Hz=5 Hz，带宽提高了6倍以上，均方根电压峰值为2.4 V，提高了近2倍。

如果进一步增大激励幅值，差别会更明显，图7为A=8 m/s2时压电俘能器频率响应。此时，俘能带宽从5 Hz增加到6 Hz，均方根电压峰值从2.4 V 增加到3.4 V。