非齐次动力学方程的一种精细积分单步方法

王 永，马 骏，李靖翔，陈汝斯，许 杨，郝跃东，胡 鹏

(1.国网上海市电力公司特高压换流站分公司，上海 201413; 2.国网湖北省电力有限公司，武汉 430070;3.南方电网超高压公司广州局，广州 510000; 4.国网湖北省电力有限公司电力科学研究院，武汉 430070)

1 引 言

目前，针对非齐次动力学方程数值解的研究成果十分丰富。常用的数值积分方法，如中心差分法、Wilson类方法、Houbolt法、Newmark类方法以及四阶经典Runge-Kutta法等，虽然应用十分广泛，但是在长时间的积分过程中会表现出能量耗散和相位误差[1]。

钟万勰[2]提出的精细积分法，由于其具有高精度和强稳定性的特点，为非齐次动力方程的时程积分提供了一种新的技术途径。对于齐次动力方程，精细积分法可以得到计算机精度的解；而对于非齐次方程，由于需要求解Duhamel积分项的数值解从而会引入数值误差[3]。针对Duhamel积分项的数值计算问题，研究人员提出了不同的技术途径[4]。(1) 近似处理，采用一般多项式、正余弦函数、指数函数及其组合形式近似代替非齐次项，并且推导出相应精细积分的递推格式； (2) 增维处理，将非齐次项也视为结构动力方程的状态变量，化非齐次为齐次，从而在源头上避免Duhamel积分项的数值误差； (3) 数值积分，采用常见的数值积分公式近似计算Duhamel积分项，从而衍生出多种精细积分格式，其中比较典型的有高斯精细法[5]、精细库塔法[6]以及高精度直接积分法[7]； (4)响应矩阵法，将Duhamel积分项转化为一系列响应矩阵的精细积分，无需进行矩阵求逆，也适用于非线性问题[8]。

近似处理法要求非齐次项本身具有特定的形式，且需要对系统矩阵进行求逆运算，因此具有很大的局限性和数值不稳定风险[3]。增维精细积分法[9]对于当Duhamel积分项为非线性和时变时的计算精度不高[10]。高斯精细法虽然计算精度较高，但是需要计算每个积分节点上的矩阵指数[8]，计算效率不高。响应矩阵法针对Duhamel积分项为非多项式和非正余弦函数也存在精度不高的问题[10]。此外，富明慧等[11]提出的广义精细积分能够得到Duhamel积分项计算机上的精确解，但是对于其形式有限制且对非线性问题无法直接使用。为此，王海波等[12]采用拉格朗日插值公式提出了对于非线性动力学分析的广义精细积分，但是计算中需要进行预估-校正；为长时间保持系统辛结构，学者将辛算法与精细积分法相结合提出了辛精细积分法[13]，但是该算法额外地增加了大量矩阵求逆运算。为减少矩阵求逆计算量，都琳等[14]提出将非齐次方程按凑微分的思想近似化为齐次形式，从而减小了矩阵求逆运算量。

本文从数值积分的角度出发，采用微分求积法计算Duhamel积分项的数值解，并采用与微分求积法同阶的显式 Runge -Kutta 法计算单步积分中的内点近似值，从而将微分求积法显式化，避免了状态矩阵求逆。算例计算结果表明，该方法继承了精细积分法和微分求积法各自的高精度和强稳定性，计算效率高，比较适用于非线性结构动力学方程的数值计算。

2 精细积分单步法

结构动力学方程的一般形式可表达为

(1)

式中M，C和K分别表示n维方阵，分别代表该系统的质量矩阵、阻尼矩阵和刚度矩阵，n表示系统的自由度数，f(t)表示施加于系统的外力项，n维向量x表示质点的位移。

(2)

式中H为n阶常数矩阵，r为非线性广义外力项。

(3)

在一个积分步长[tk,tk + 1]内，非齐次动力方程(2)的解可表达为同解积分方程(4)

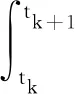
(4)

式中 等式右边第一项中的指数矩阵T=eHΔt可以采用加法定理精细积分得到，第二项积分与系统特征有关，称为Duhamel积分项。由于第一项的计算可以由精细积分达到计算机精度，因此数值误差主要来源于Duhamel积分项的数值计算误差。本文采用时域微分求积法计算Duhamel积分项。

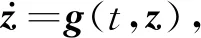
(i=1，2，…，s) (5)

式中 Δt是积分步长；cj表示网格点；ai j和bj是与网格点相关的积分系数[16]。

(6)

式中ti=tk+i×Δt/s。

(7)

式中S1=Hvk+r(tk,vk)

(8)

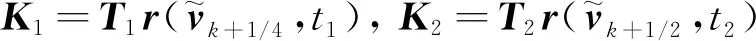
T1=eH 3Δ t/4,T2=eH Δ t/2,T3=eH Δ t /4

且有T2=T3×T3，T1=T2×T3，T=T1×T3

(9)

注意，对于线性动力学方程，预估计算可以省略，从而可以极大地提高计算效率。

3 算例分析

线性的二自由度动力学方程：

(10)

其解析解如下,

式中x1(0)=x2(0)=x3(0)=x4(0)=0。

取仿真步长Δt=0.2 s，积分时程为12 s，分别采用本文方法(s=4，简记为DQM4)和精细库塔法(简记为RK4)求解，结果相对于解析解的绝对误差的绝对值(记为R(·))曲线如图1所示。

可以看出，对于线性、非刚性的非齐次动力方程，本文方法在精度上略高于精细库塔法。尽管经典四阶RK方法是条件稳定的，而s级时域微分求积法是无条件稳定的，但是长时间的数值积分后二者都可以精确刻画系统的位移变化轨迹。这说明对于非刚性系统，同阶的本文方法与精细库塔法的计算特性相似。

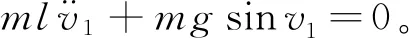
式中 初值v1(0)=1.0472,v2(0)=0。

以椭圆积分得到该问题的解析解为基准，分别采用本文方法(DQM4)和精细库塔法计算幅角v1，计算步长Δt取0.1 s和0.01 s，并与文献[1]的预估校正-辛时间子域法、文献[4]的基于精细积分的Taylor级数单步法(T-PIM)和文献[17]的高效单步法做对比。相应的计算结果列入表1和表2。图2是精细库塔法和本文方法计算的幅角v1的变化曲线。可以看出，精细库塔法的数值解已经发散，而本文方法可以稳定地长时间计算。这是因为计算Duhamel积分项的经典四阶RK方法是条件收敛的，当计算误差积累到一定程度时，积分结果将严重偏离系统真实解。相反，由于s阶时域微分求积法是无条件稳定的，因此可以采用大步长计算Duhamel积分项，而不会发生数值发散现象。

图1 精细库塔法与本文方法的精度比较

Fig.1 Accuracy comparison between precise -Kutta method and this method

从表1和表2可知，本文方法的计算精度要明显高于预估校正-辛时间子域法、T-PIM和文献[17]的方法，与椭圆积分解保持高度一致。并且随着计算时间的积累，这种现象越明显。计算步长取Δt=0.1 s，本文方法长时间计算结果的局部与椭圆积分解的对比如图3所示。可以看出，本文方法可以长时间跟踪单摆的运动轨迹，说明本文方法具有高精度和良好的稳定性。

算例3受迫Duffing方程为

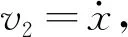
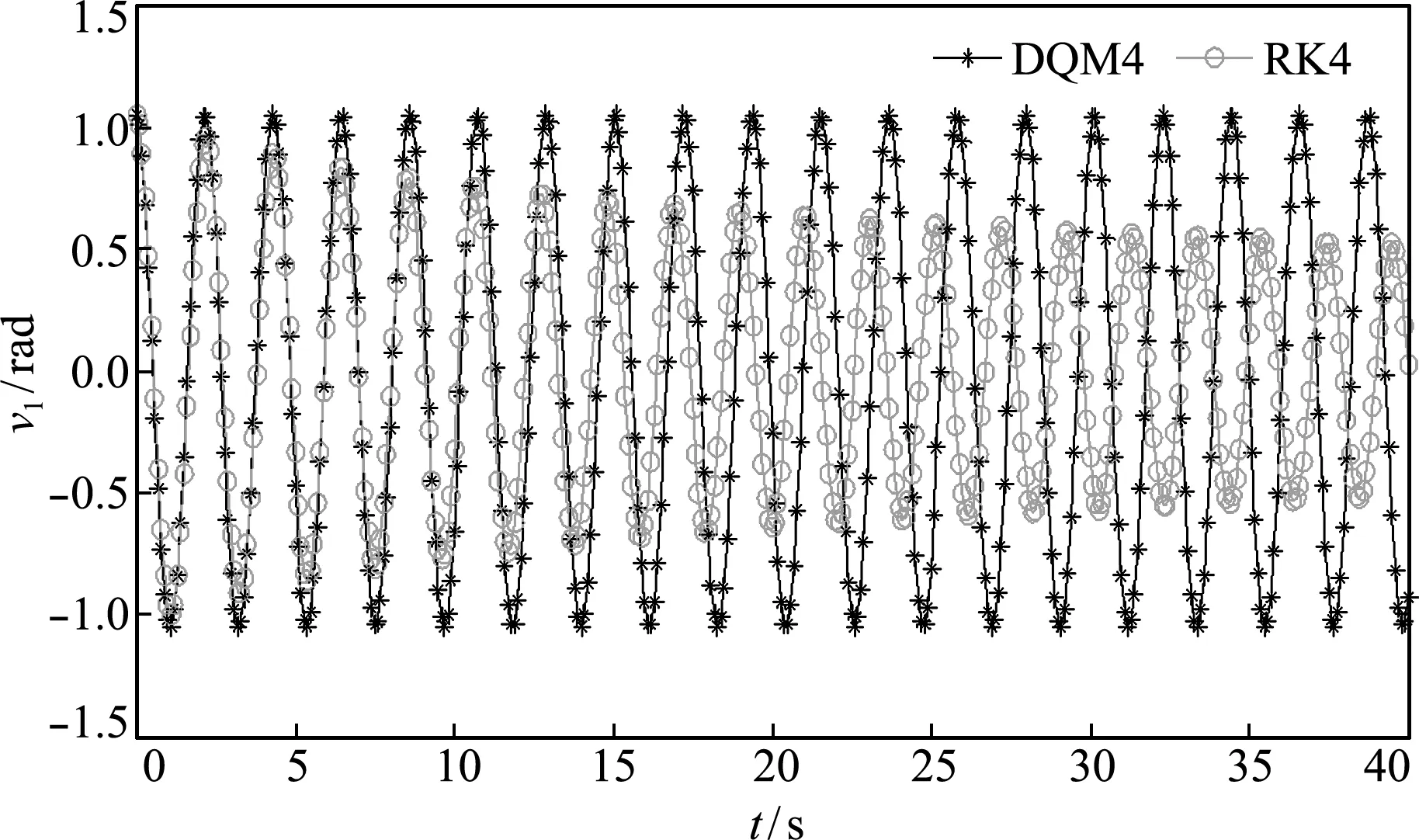
图2 幅角时程曲线

Fig.2 Time history curve of pendulum angle

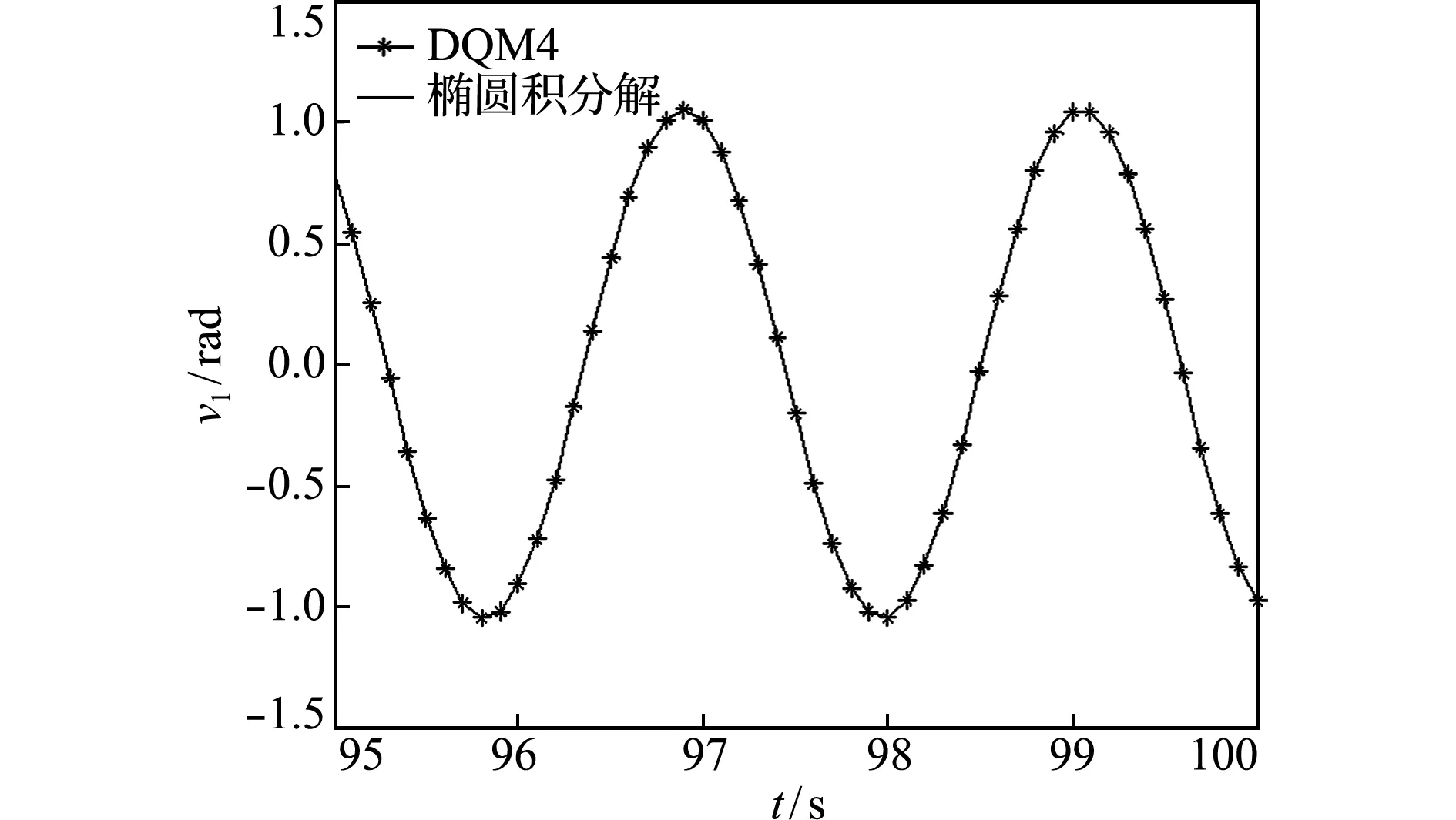
图3 长时间计算结果对比

Fig.3 Long -term calculation results comparison

在α=0.4,k=-1,β=1和ω=1.3的条件下，取时间步长Δt=0.1 s，振幅f依次取0.35和 0.41，系统的初始值为[v1,v2]=(2.0,0.0)。采用本文方法计算该方程的数值解，绘制出相应的相图(局部)如图4和图5所示，计算到400 s为止。

可以看出，振幅f取0.35和0.41时分别对应于系统的一周期和四周期响应。相应的计算结果与其他方法对比情况列入表3，其中四阶显式 Runge -Kutta 的计算步长为Δt=1.0 ms，本文方法和预估校正-辛时间子域法的计算步长为Δt=0.1 s。由表3可知，本文方法的大步长计算结果与小步长的四阶RK方法吻合得非常好，且比预估校正-辛时间子域法的计算精度高，说明本文方法具有较高计算精度和良好的数值稳定性。

表2 幅角v1的数值结果对比(Δt=0.01 s)Tab.2 Comparison of pendulum angle (Δt=0.01 s)

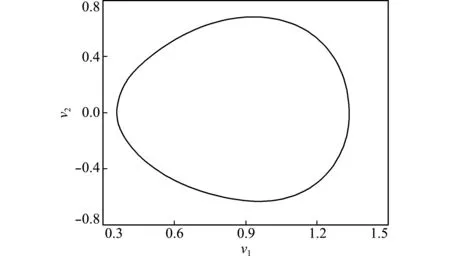
图4f=0.35的周期响应

Fig.4 Period response forf=0.35

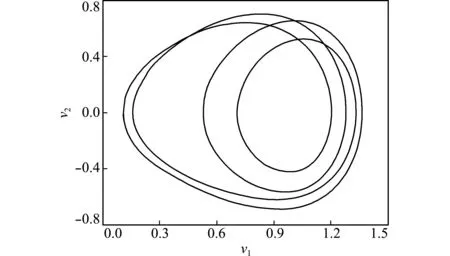
图5f=0.41的四周期响应

Fig.5 Period response forf=0.41

表3 受迫Duffing方程x计算结果对比

Tab.3 Comparison ofxfor Duffing equation

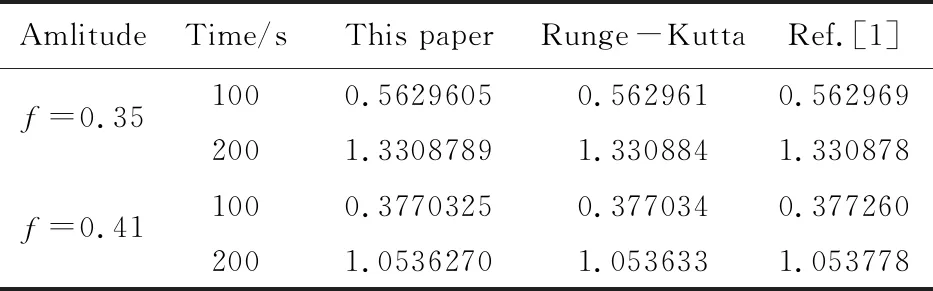
AmlitudeTime/sThispaperRunge-KuttaRef.[1]f=0.351000.56296050.5629610.5629692001.33087891.3308841.330878f=0.411000.37703250.3770340.3772602001.05362701.0536331.053778

4 结 论

本文将结构动力学方程转化为非齐次动力方程，通过对未知量的显式预估，建立了求解非齐次动力方程精细积分-微分求积法PIDQM(precise integration-differential quadrature method)，并给出了通用的计算公式。不仅解决了微分求积法求解非线性常微分方程存在的巨大计算量问题，而且为精细求积法应用于求解非线性动力系统提供了一种新的思路。本文方法可以避免状态矩阵求逆，无需对非线性项求导数，计算格式紧致，便于编程实现。对两自由度的线性微分动力系统、非线性单摆和Duffing方程的计算分析表明，本文方法具有较好适应性，且计算精度比现有的单步法和预估校正-辛时间子域法高，即使采用大步长积分，经历长时间的积分过程仍能保持较好的计算精度和数值收敛性。因此，本文建立的精细积分-微分求积法是多自由度结构体系的非线性动力学分析的一种有效方法。