多激励下结构反共振频率的计算和配置
2023-11-20史英沙
史英沙,黎 胜
(1.大连理工大学工业装备结构分析国家重点实验室,辽宁 大连 116024;2.大连理工大学船舶工程学院,辽宁 大连 116024)
引言
在结构动力学中,反共振是指系统的某个自由度在特定频率下的稳态振动幅值为零[1]。因此反共振在结构的局部振动控制中具有重要的应用价值。目前反共振主要应用于结构的隔振系统[2-5]。反共振是系统的局部现象,不仅与结构的质量和刚度相关,还与激励位置和响应输出位置相关,不同的激励位置和响应输出位置存在不同的反共振频率。目前对反共振的研究主要是考虑单个激励的作用,而在实际工程应用中,结构受力较为复杂,有时会受到多个激励力甚至是分布力的作用,此时结构某个自由度的振动响应与所有的激励力大小及其位置相关。因此在多个激励力,甚至是分布力作用时,分析和研究结构某一位置的振动响应为零的频率具有重要意义。目前的文献主要是针对单输入单输出时的反共振频率的计算和灵敏度分析[6-8]。对单输入单输出时的反共振频率的计算方法主要有两种:划去质量阵和刚度阵的相关行和列来构造子矩阵方法,以及Wang 等[6]使用的零空间构造矩阵方法。前者无法应用于多个激励作用下的反共振频率的计算,后者虽可以计算多个激励作用下的反共振频率,但构造出的矩阵没有明确的物理意义,难以应用于对反共振频率的配置中。
在结构的动力学控制中,根据不同需求使用主动方法或被动方法对结构的反共振频率进行配置,以达到在稳态激励下某一位置振动响应为零的目的。Mottershead[9]使用测量导纳方法对原点导纳或跨点导纳的反共振频率进行配置。Kyprianou 等[10]证明通过附加质量弹簧简单振子可以实现对任意反共振频率的配置。Mottershead 等[11]使用主动振动控制对反共振频率进行配置。Tsai 等[12]使用逆结构修改方法同时配置一个导纳函数的两个反共振频率。但是上述文献主要关注于单激励系统的反共振频率配置,而对多个激励力作用时的反共振频率配置研究较少。Shi 等[13]基于测量导纳的结构修改方法提出了在结构受到多个力作用时的反共振频率的配置,但该方法局限于对一个反共振频率的配置,并且不能直接计算得到反共振频率。目前通过部分特征结构配置的方法可实现对多个共振频率的配置[14-17],而对多个反共振频率的配置研究较少。若部分特征结构配置方法可应用于反共振频率的配置,将对结构的局部振动控制具有重要的意义。
本文主要计算和配置了结构受到多个激励力时的反共振频率,通过构造矩阵,使得矩阵的特征值为多激励作用下的反共振频率,从而实现对复杂激励下反共振频率的直接计算。并且基于上述反共振频率的计算方法可把部分特征结构配置方法应用于对多个反共振频率的配置中,从而实现对多激励作用下反共振频率的配置。本文分别利用了质量阵/刚度阵修改以及附加一个自由度的简单振子的修改方法,对多激励作用下结构的一个或两个反共振频率进行配置。以线性面载荷激励下的矩形钢板为例研究了分布力下反共振频率的计算和配置,并以多个力激励下的六自由度质量弹簧系统为例研究了多激励下的反共振频率的计算和配置。
1 理 论
1.1 多激励作用下反共振频率的计算
无阻尼结构受迫振动时,系统的运动方程为:
式中M和K分别为结构的质量阵和刚度阵;ω为激励力频率;x为位移向量;F为节点激励力向量。
当结构受到分布力作用时,可将分布力转换为等效节点力F进行计算。系统的位移响应为:
式中Z-1(ω)=H(ω)为结构的导纳矩阵,矩阵元素hpq的求解公式为:
式(3)中分母为零的频率为结构的共振频率。当分子adj(K-ω2M)pq=0 时,所求频率即为激励力作用在q自由度时,p自由度的响应输出为零的反共振频率。
结构受到多个激励作用时,p自由度处的振动位移响应为:
当位移xp=0,式(4)可写为:
根据行列式性质,式(5)可转化为用激励力向量转置FT来替换阻抗矩阵Z的p行元素的行列式,即为:
式中zij=kij-ω2mij,其中i,j=1,…,n;F为实向量。
因此在求解式(6)时可将系统的刚度阵、质量阵中p行元素 分别替换为kpr=fr,mpr=0,其中r=1,…,n,从而形成新的矩阵和,并且式(6)可转化为广义特征值问题的形式:
式(7)求得的特征值即为多激励作用下p自由度的反共振频率,特征向量没有具体的物理意义。结构仅有部分自由度受到激励力时,其他自由度的激励力为零,利用上述方法依旧可求解此时的振动位移响应为零的频率。
1.2 多激励作用下反共振频率的配置
1.2.1 基于结构修改的多激励下反共振频率配置
无阻尼结构自由振动时的运动方程为:
公式(8)的广义特征值为结构共振频率的平方ω2,而公式(6)和(7)的特征值为多个激励力作用下结构反共振频率的平方。目前相关文献可通过对结构特征值进行配置实现对共振频率的配置。参考Mottershead 等[18]对共振频率和振型节点的配置方法,可实现多个激励力甚至分布力作用下结构反共振频率的配置。
根据文献[18]中的配置方法,在对多激励作用下的结构反共振频率ωa配置时,公式(7)左乘,可得到如下等式:
式中I为单位阵;kg为g自由度的刚度修改量,且修改位置与响应输出位置不相同,即p≠g。
根据公式(9)可以得到在位移响应位置p处和结构修改位置g处的等式分别为:
同理,对结构进行质量修改时,在响应输出位置和修改位置的等式分别如下:
令xp=0,可得到质量修改量为:
在构造广义特征值时用激励力向量替换了结构阻抗矩阵中响应位置的相关元素,因此该结构修改方法仅适用于配置一个响应输出位置的反共振频率,而无法同时配置多个位置的反共振频率。目前已有相关文献通过对特征值的配置实现对多个共振频率的配置。因此基于相关计算方法也通过对构造特征值的配置实现多激励作用下多个反共振频率的配置。
1.2.2 附加一个自由度的简单振子的反共振频率配置
Kyprianou 等[10]通过对系统附加一个质量弹簧系统来配置共振频率的方法可扩展应用于反共振频率的配置。其配置共振频率的方法如下文所述,在配置多激励作用下的反共振频率时仅需将文献[10]中的刚度阵K和质量阵M分别替换为公式(7)中的Kˉ和Mˉ。
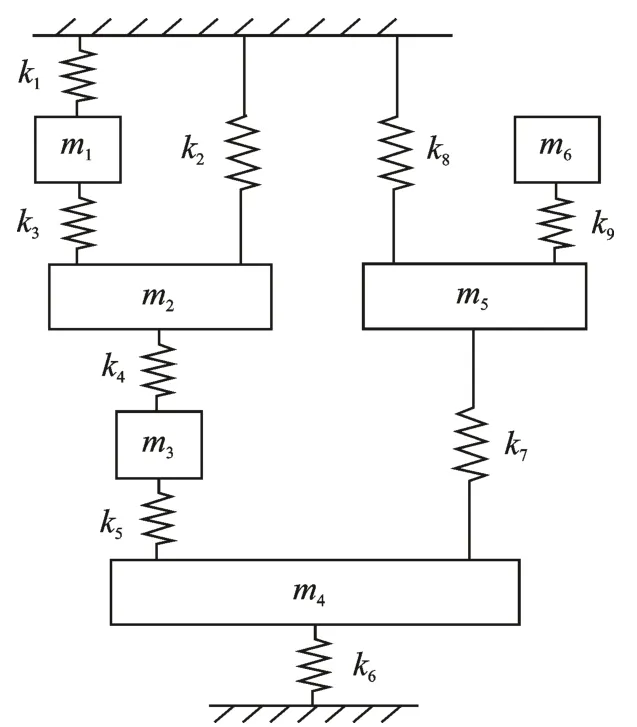
假设结构有n个自由度,并且在第n个自由度处增加一个简单振子,如图1 所示。简单振子连接的自由度n与反共振响应输出自由度p不同,即n≠p。
1.2.1 对照组 采用胃肠动力药+氟哌噻吨美利曲辛片+双倍PPI[3]。给予枸橼酸莫沙必利分散片(成都大西南制药有限公司,国药准字:H20031110)5mg,3次/d,饭前服用,氟哌噻吨美利曲辛片(黛力新,丹麦,深圳市康哲药品有限公司,进口药品注册证号:H20080175)1粒,2次/d,于早、晚餐后服用,艾司奥美拉唑镁肠溶片 (阿斯利康制药有限公司,国药准字:H20046379)40mg,2 次/d,共服 8 周。

图1 连接在第n 个自由度上的简单振子Fig.1 Simple oscillator connected to the nth degree of freedom
简单振子的质量和刚度分别为dm和 dk。此时结构的运动方程为[10]:
式中 等式左侧zij=kij-ω2mij,其中i,j=1,…,n,是求解特征值的系统阻抗阵。
根据文献[10]公式推导,求解系统特征值的等式为:dk-ω2dm-ω2dmdkhnn=0。在式(14)中存在两个未知量dk和dm。
当配置一个特征值频率ωi时,简单振子的刚度为[10]:
式中hnn(ωi)为连接简单振子的结构自由度n的原点导纳频响函数。为了令dk>0,质量和特征频率应满足不等式[10]:
当同时配置两个特征频率ωi和ωj时,振子的质量为[10]:
为了使得dm>0,特征频率及连接位置的自由度的导纳函数需要满足以下不等式[10]:
2 数值算例
2.1 矩形板反共振频率的计算和配置
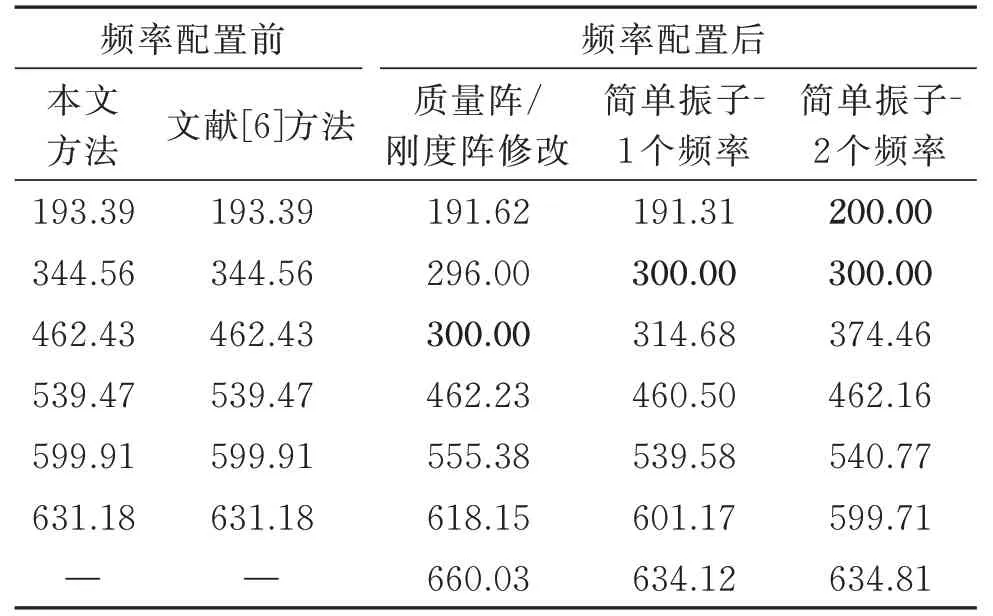
表1 节点a 的反共振频率(单位:Hz)Tab.1 Antiresonant frequency of node a(Unit:Hz)

图2 受线性面载荷的矩形板Fig.2 The rectangular plate subjected to a linear surface load
首先通过对结构质量阵/刚度阵修改的方法将300 Hz 配置为节点a 的反共振频率,选择修改的位置为节点b,通过质量阵/刚度阵修改方法得到需要的修改量为:Δk=-2.992×106Nm 或Δm=0.842 kg。在节点b 增加质量后,节点a 的反共振频率见表1(质量阵/刚度阵修改),并且节点a 的频响曲线如图3 所示。结构修改后节点a 在300 Hz 的振动响应为零,即通过结构修改把300 Hz 配置为节点a 的反共振频率。
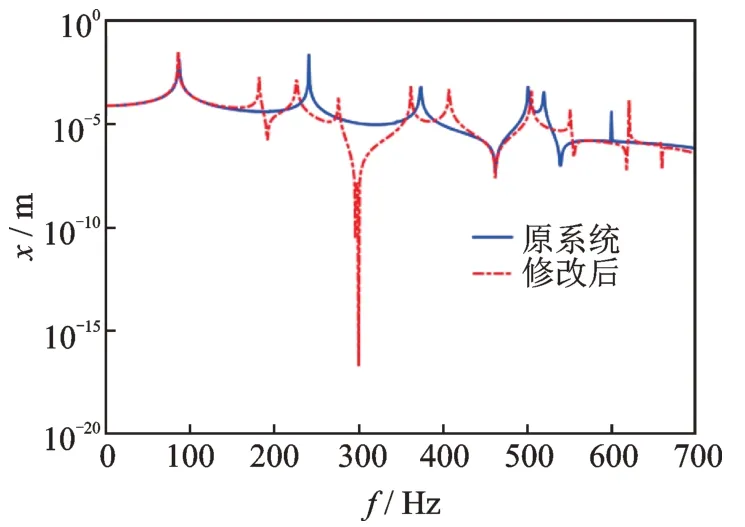
图3 质量修改后节点a 的频响曲线Fig.3 Frequency response curves of node a after mass modification
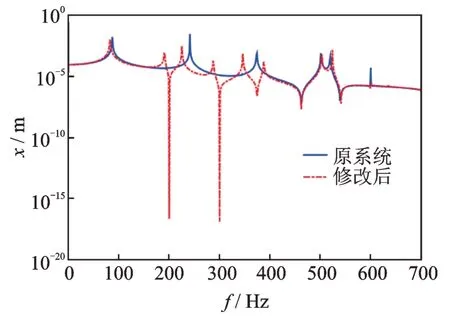
此外也可通过附加简单振子的方法将300 Hz配置为节点a 的反共振频率。在实际工程中可根据已知约束选择符合要求的简单振子的连接位置、质量和刚度。在本算例中要求简单振子的质量和刚度都较小。选择振子的质量和刚度时,首先根据不等式(16)计算连接在不同节点时振子质量的取值范围,然后选取令不等式(16)在各个节点时均成立的振子质量dm,再通过公式(15)计算连接在各节点时振子的刚度dk,最后选取最小dk为振子刚度,它的节点为简单振子的连接位置。在本算例中振子连接在不同节点时不等式(16)均成立的质量范围为0 图4 简单振子-1 个频率节点a 的频响曲线Fig.4 Frequency response curves of node a attached to simple oscillator after assigning one frequency 当使用简单振子将200 和300 Hz 同时配置为节点a 的反共振频率,在选取振子附连的位置时需要满足不等式(18),并且要求振子的质量和刚度都较小。在本算例中根据公式(17)振子附加在节点d 时振子质量最小为dm=0.1187 kg,此时振子的刚度为dk=3.5186×105N/m。附加后的节点a 的反共振频率见表1(简单振子-2 个频率),频响函数曲线如图5 所示。配置后200 和300 Hz 已是节点a 的反共振频率,见表1 和图5。 图5 简单振子-2 个频率节点a 的频响曲线Fig.5 Frequency response curves of node a attached to simple oscillator after assigning two frequencies 以六个自由度的质量弹簧系统为例[18],如图6 所示,质量块1~6 的激励力向量为FT=[1 2 3 4 5 6]T,此时分别使用本文方法和文献[6]中方法计算得到质量块1 的反共振频率,如表2 所示。 表2 质量块1 的反共振频率(单位:Hz)Tab.2 Antiresonant frequency of mass block 1(Unit:Hz) 图6 六自由度质量弹簧系统Fig.6 The mass-spring system of six degrees of freedom 若使用质量阵/刚度阵修改方法将1.5 rad/s 配置为跨点导纳h45的零点时,在第3 自由度处进行刚度修改,通过公式(11)计算得到刚度的修改量为=0.4605 N/m,与文献[9]中的刚度修改计算结果相同。 质量弹簧系统受到多个激励时,根据表2 中质量块1 的反共振频率,要求将0.15 Hz 配置为质量块1 的反共振频率。使用质量阵/刚度阵修改方法对第6 自由度处进行结构修改,计算可得Δk6==0.1707 N/m。修改后质量块1 的反共振频率见表2,且质量块1 处的位移频响曲线如图7 所示。由表2 和图7 可知,在多个激励力作用下,质量块1 在0.15 Hz 的振动位移响应为零。 图7 结构修改前后质量块1 处的位移响应曲线Fig.7 Displacement response curves of mass block 1 before and after structural modification 通过对结构附加简单振子来配置质量块1 在多个激励下的反共振频率0.15 Hz,此时通过和构造的矩阵的原点导纳分别为h=[0.1516 0.2459 1.5117 1.0699 -0.3278 -5.8597]。可计算得到简单振子连接在各自由度时均满足不等式(16)的振子质量dm的范围,即当0 图8 附加简单振子前后质量块1 处的位移响应曲线Fig.8 Displacement response curves of mass block 1 before and after attaching a simple oscillator 通过附加简单振子同时配置2 个反共振频率时,假设质量块1 分别在0.15 和0.25 Hz 的振动位移响应为零。计算发现只有将简单振子连接在质量块2 或3时,dm>0,dk>0,以及不等式(18)才得以满足,此时它们的质量和刚度分别为dm2=1.0562 kg,dk2=1.2195 N/m;dm3=0.3824 kg,dk3=0.6983 N/m。以连接的简单振子的质量和刚度小为原则,选取将简单振子连接在位置3 处。结构修改后使得质量块1的位移为零的频率见表2(2 个频率),附加前后的位移频响曲线如图9 所示。数值结果显示使用附加简单振子后质量块1 在两个配置频率0.15 和0.25 Hz处的振动位移为零。 图9 配置2 个频率时质量块1 处的位移响应曲线Fig.9 Displacement response curves of mass block 1 at after assigning two frequencies 本文提出了一种计算结构在多激励作用下某自由度振动位移为零的频率的方法。该方法通过结合激励力向量与质量阵和刚度阵从而构造出新的线性矩阵,使得矩阵的广义特征值为多激励作用下结构的反共振频率,并使用部分特征值配置方法实现了多激励作用下结构的反共振频率的配置。在本文中分别计算和配置了线性面载荷激励的矩形板和多个激励下的六自由度系统的反共振频率。数值结果表明,结构在多激励或分布力作用下的计算方法和配置方法的有效性,为结构复杂受力下的反共振频率的研究提供了参考。
2.2 六自由度质量弹簧系统反共振频率的计算和配置




3 结论
