幂律型浆液扩散压力环向分布模型
2020-05-22杨双锁
黄 轩,杨双锁
(太原理工大学 矿业工程学院 地下工程系,太原 030024)
1 引 言
盾构开挖施工过程中,盾尾壳体脱离管片以后,由于盾构壳体内径大于管片直径、盾壳本身厚度以及超限开挖等因素,开挖掘进过程中会留下盾尾间隙。若不有效处理盾尾间隙,会造成地表变形对地面道路和构筑物产生破环影响[1]。施工一般采取壁后注浆的方法来及时填充形成的空隙。而注浆压力作为壁后注浆中的一项重要施工参数,首先影响浆液的充填、扩散和分布等情况,并最终影响注浆效果。
长期以来,学者致力于研究壁后注浆浆液扩散模型,并提出多种理论。杨秀竹等[2]基于广义达西定律,对幂律型浆液及其渗透范围进行了研究。苟长飞等[3]利用流体力学理论,研究了浆液扩散环形模型,并推导了理论计算公式。叶飞等[4,5]利用毛细管组理论,提出了注浆时渗透扩散模型,并用工程实际数据进行验证。Baker[6]运用裂隙注浆理论,研究牛顿型流体浆液扩散半径,得出了扩散范围的最大值。张庆松等[7]基于浆液粘度随时间的变化,分析了注浆时间、注浆压力及注浆扩散半径三者之间的关系。杨志全等[8-10]基于柱型扩散和球形扩散两种模型,对宾汉姆流体和幂律型流体扩散半径进行了推导。袁小会等[11]研究硬性浆液扩散半径,完成了相应的计算公式推导。周佳媚等[12,13]考虑浆液稠度变化因素来研究盾构壁后注浆扩散模型,并建立恒定注浆速率条件下盾构隧道壁后注浆渗透扩散模型。
结合前面学者的众多研究,目前对于浆液扩散模型以及注浆压力和半径的研究取得很多成果。但是在研究推导过程中,均只考虑浆液扩散过程中管片表面以及扩散土体边界面为阻力作用面,忽略了在注浆过程中盾尾断面新注入浆液与已注入浆液间的阻碍作用[14,15]。本文考虑盾尾断面新注入浆液与已注入浆液间阻碍作用,利用环向分布模型,对幂律型浆液扩散压力环向分布计算式进行了推导,并结合工程实例进行验算。
2 浆液扩散压力环向分布模型
2.1 扩散机理
盾尾间隙采用同步注浆的方法进行浆液填充时,浆液从注浆孔流至两孔间最远距离需要的时间很短,较盾构机推进速度来说,可以认为此时在盾尾空隙处,存在一个三维环形将其填充如图1所示,且三维环形厚度(图1中δ,数量级可认为是10-2m)远小于三维环形宽度(图1中b,数量级可认为是10-1m)。所以在环向分布模型中,只考虑浆液环向流动。本文研究六孔注浆,如图2所示。
2.2 基本假定
为建立浆液扩散压力环向分布模型,做以下假定。
(1) 浆液为不可压缩各项同性均质流体,扩散过程中一直符合幂律型流体特性,不考虑浆液粘度时变性。
(2) 浆液与土体及管片之间均为不透水边界,流体力学连续性方程恒成立。
(3) 充填过程中浆液只沿环向流动,三维环形厚度与相同时间内盾构机掘进距离相等。浆液流动过程中不发生堵塞和稀释等现象。
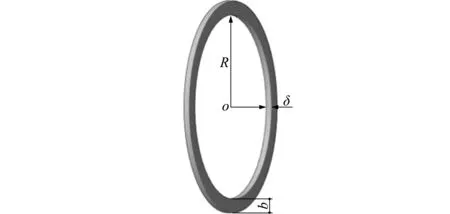
图1 三维环形充填模型
Fig.1 Three -dimensional annular filling model
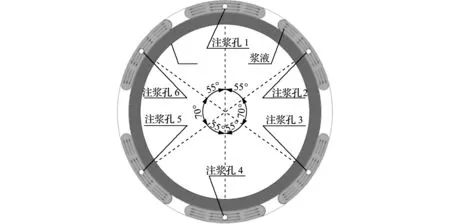
图2 六孔注浆横断面
Fig.2 Six hole grouting cross section
3 理论推导
3.1 公式推导
根据以上基本假定,以三维环形厚度及巷道轴线方向为z轴,水平方向为x轴,竖直方向为y轴建立坐标系,如图3所示。图3中R为管片半径,δ为三维环形厚度,α为偏离注浆孔的角度,b为三维环形宽度也就是尾部孔隙宽度。在充填过程中任取一单元体,对其进行受力分析,如图3所示。
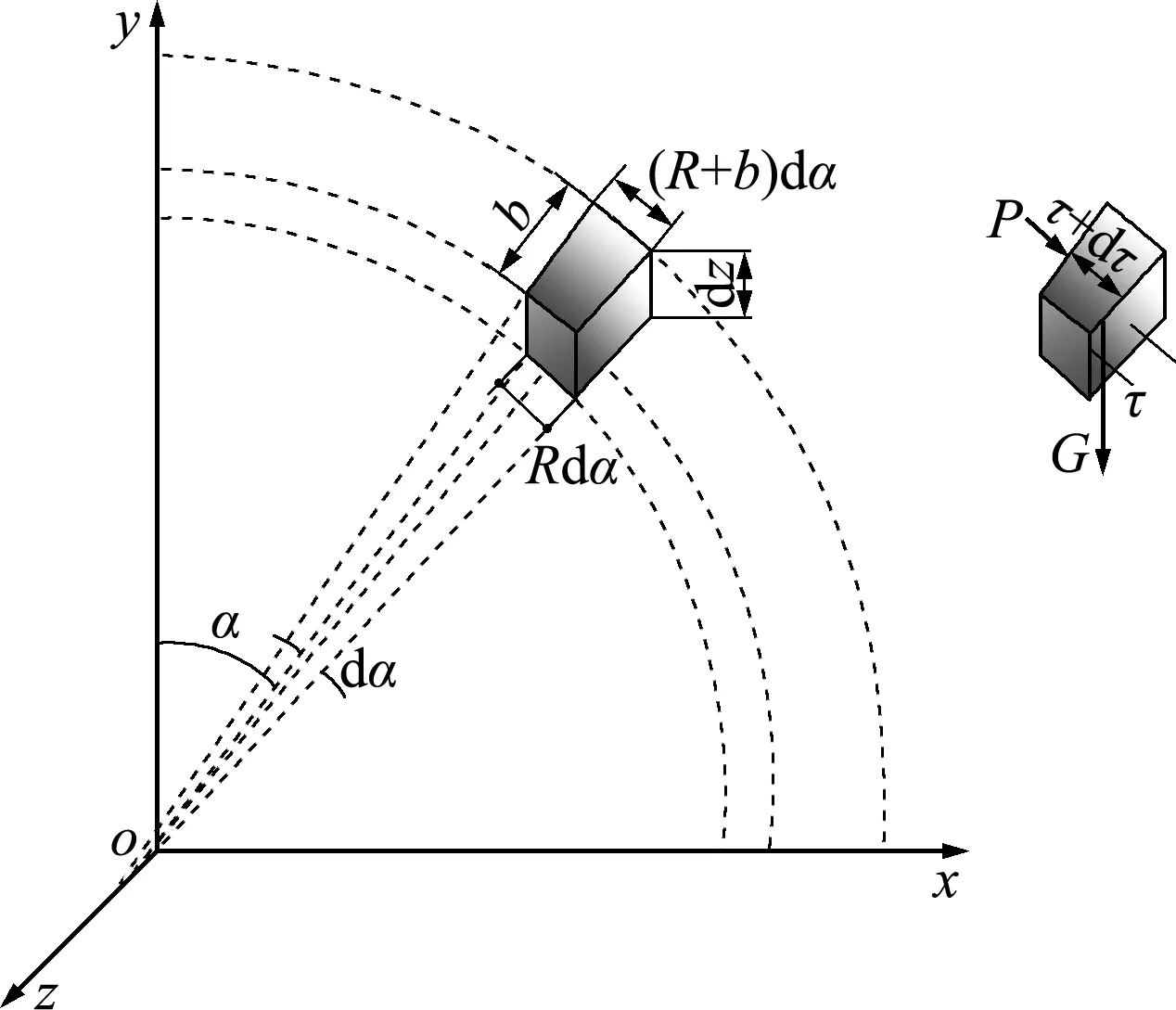
图3 坐标系建立及受力分析
Fig.3 Coordinate system establishment and force analysis
通过应力平衡可得
Pbdz-(P+dP)bdz+ρgsinα·b·
(R+b/2)dα·dz+τb(R+b/2)dα-
(τ+dτ)b(R+b/2)dα=0
(1)
式中P是注浆压力,τ是单元体切应力,g是重力加速度。因为b≪R,所以R≈R+b/2,化简可得
(2)
沿Z方向积分,利用边界条件,z=0时,τ=0,得
(3)
记ρgRsinα-dP/dα=B
(4)
将式(3)化简为
τ=Bz/R
(5)
壁后注浆一般为水泥基浆液,当水灰比W/C=0.5~0.7时,浆液是幂律型流体[16]。此时,幂律型流体流变方程为
τ=μγn
(6)
μ为稠度系数,n为流变指数,γ为剪切速率,γ=-dv/dz,即
τ=-μ(dv/dz)n
(7)
将式(7)代入式(5),得
dv=[-B/(Rμ)]1/nz1/ndz
(8)
式(8)沿z方向积分,利用边界条件z=δ/2时,v=0,得到浆液速率扩散分布为
v=[Bn/Rμ(n+1)][(δ/2)(n + 1)/n-z(n + 1)/n]
(9)
幂律型浆液流速分布如图4所示。可得截面流量
{n2/[Rμ(n+1)(2n+1)]}·
(10)
由式(10)可得
{n2/[Rμ(n+1)(2n+1)]}·
(11)
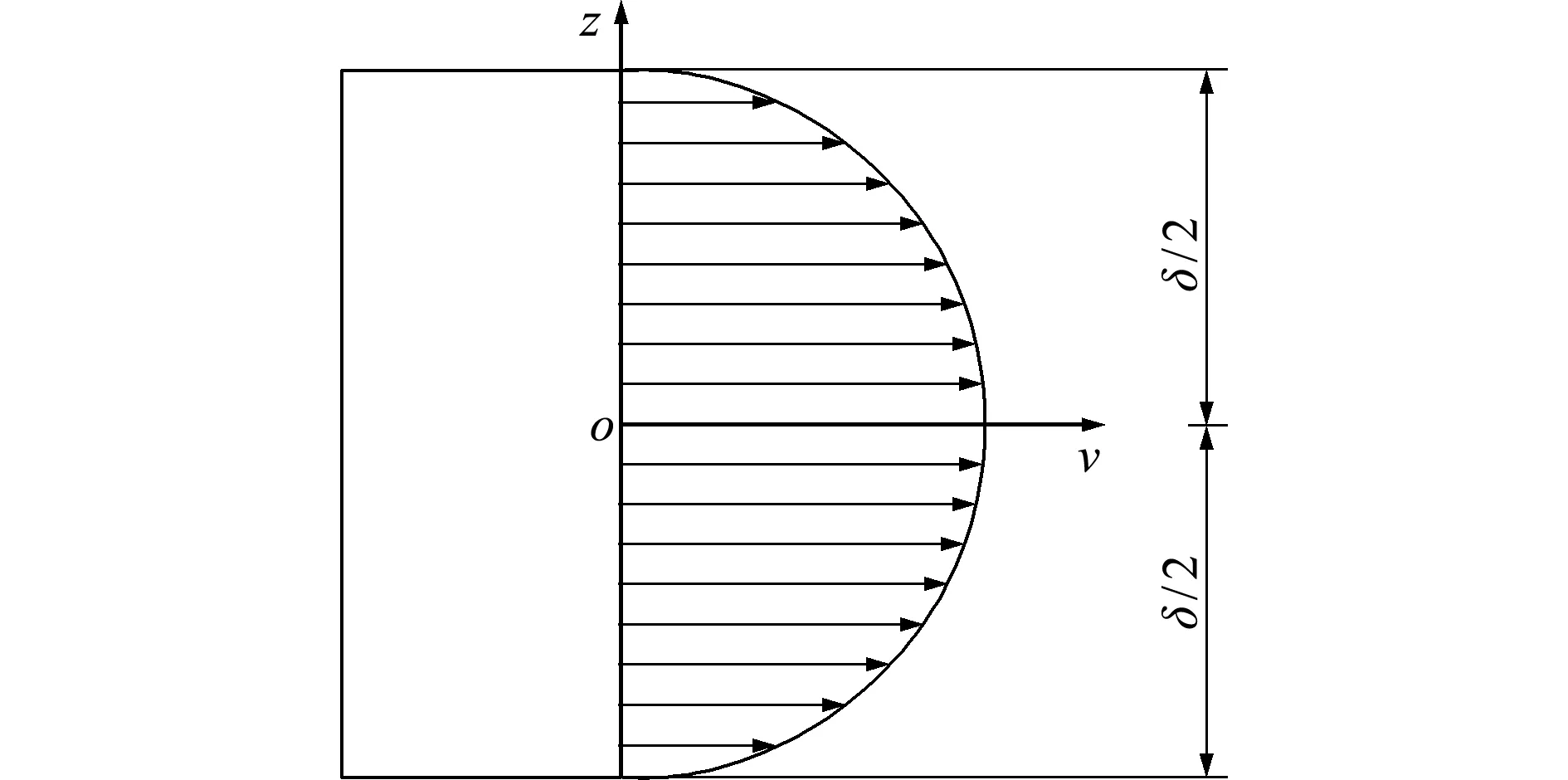
图4 幂律型流体速度分布
Fig.4 Power law fluid velocity distribution

通过复习课,学生具备了相对稳固的知识体系,具备了一定的科学探究能力与问题解决能力。教师可以引导学生结合本地资源开展多种形式的科学实践活动,尝试解决现实生活中与生物学息息相关的问题,进行社会责任的渗透。
{n2/[Rμ(n+1)(2n+1)]}·
[(δ/2)(2n + 1)/n-(-δ/2)(2n + 1)/n]
(12)
式(11)化简为
B=q/(bK)
(13)
将式(13)代入式(4)得
dp=[ρgsinα-q/(bK)]dα
(14)
式(14)沿α方向积分,利用边界条件α=α1,P=P1(P1为孔位1的注浆压力,α1为孔位1偏离竖直中线的角度),得到孔位1向下方注浆时,浆液扩散压力分布计算式为
P=P1+ρgR(cosα1-cosα)+[q/(bK)](α1-α)
(15)
同理可得,孔位1向上注浆时的扩散压力分布计算式为
P=P1+ρgR(cosα1-cosα)-[q/(bK)](α1-α)
(16)
P=Ps+ρgR(cosαs-cosα)±[q/(bK)](αs-α)
(17)
式中S为注浆孔序号,+代表该孔位向下注浆,-代表该孔位向上注浆。
式(17)的截面流量q,由式(18)来确定,
(18)
v盾为盾构机推进速度,β为浆液注入率,l为注浆孔个数。
3.2 适用范围
同步注浆按注浆孔所在位置的不同可以分为盾尾注浆以及管片注浆。式(17)适用于壁后注浆中盾尾注浆,而不适用于壁后注浆,因为管片注浆时注浆位置位于管片,并没有直接填充盾尾孔隙。注浆孔个数一般为4孔或者6孔,此公式皆适用。
4 实例计算
4.1 工程概况
某矿为盾构机掘进,注浆孔布置和注浆压力列入表1。浆液水灰比W/C=0.5,稠度系数μ= 10.5,流变指数n=0.2,浆液密度ρ=2190 kg/m3,重力加速度g=9.8 m/s2。管片外半径R=4.725 m,盾尾间隙b=0.16 m,三维环形厚度δ=0.0216 m。盾构机推进速度取0.0008 m/s,浆液注入率取150%。
4.2 实测与计算结果
截面流量为
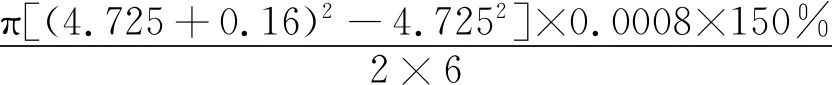
4.8305×10-4m3/s
将以上参数代入式(17),得到幂律型浆液扩散压力环向分布计算结果。计算偏离1号注浆孔30°处注浆压力(即α1=30°),此时K=3.09×10-6,其余各处计算方法同理,计算过程如下。
P=P1+ρgR(cosα1-cosα)+q/(bK)(α1-α)=
200×103+2190×9.8×4.725(cos60°-cos0)+
对比计算得到的注浆压力与实测数据,如图5所示。可以看出,由于受浆液自重影响,注浆孔向上注浆时注浆压力小于向下时注浆压力。幂律型浆液计算值略小于现场实测值,且实测值曲线较计算值光滑。但两者压力分布均呈现出圆环状分布,整体误差不大,证明了幂律型浆液扩散压力环向分布计算式的可实用性。计算结果可为相关工程提供理论借鉴。
表1 注浆孔压力
Tab.1 Grouting hole pressure

注浆孔编号角度α/(°)注浆压力/kPa102002552303125340418037052353406305230

图5 计算结果与实测值对比
Fig.5 Calculated results are compared with the measured values
4.3 牛顿浆液与幂律型浆液比较
由流体力学理论可知,当稠度系数n=1时,即为牛顿浆液。故n=1时,式(17)即为牛顿浆液扩散压力的环向分布计算式。此时取水灰比W/C=2,稠度系数μ=2,代入式(17)得到牛顿流体扩散压力的环向分布。从图6可以看出,牛顿流体计算值略大于幂律型流体计算值。因为幂律型浆液流动阻力大于牛顿流体浆液,在扩散过程中,压力损失较牛顿流体多,所以环向扩散压力小于牛顿流体浆液。
4.4 水灰比对环向扩散压力的影响
浆液水灰比发生变化时,流体的流变方程也会相应改变。 本文研究不同水灰比对浆液扩散压力环向分布模型的影响,为比较其差异,分别取不同水灰比下扩散压力的最大值和最小值比较(即底部注浆孔和顶部注浆孔对应值),注浆孔压力按 表1 计算。水灰比对应的C和n值列入表2,比较结果如图7所示。
当水灰比从0.5增加至0.7时,顶部和底部注浆孔扩散压力均呈现减小趋势,但减小速度较为缓慢。调整幂律型浆液水灰比可以适当调节浆液扩散压力,但顶部注浆孔与底部注浆孔注浆压力差值较大,说明注浆孔的注浆压力在浆液压力扩散中起主导作用。
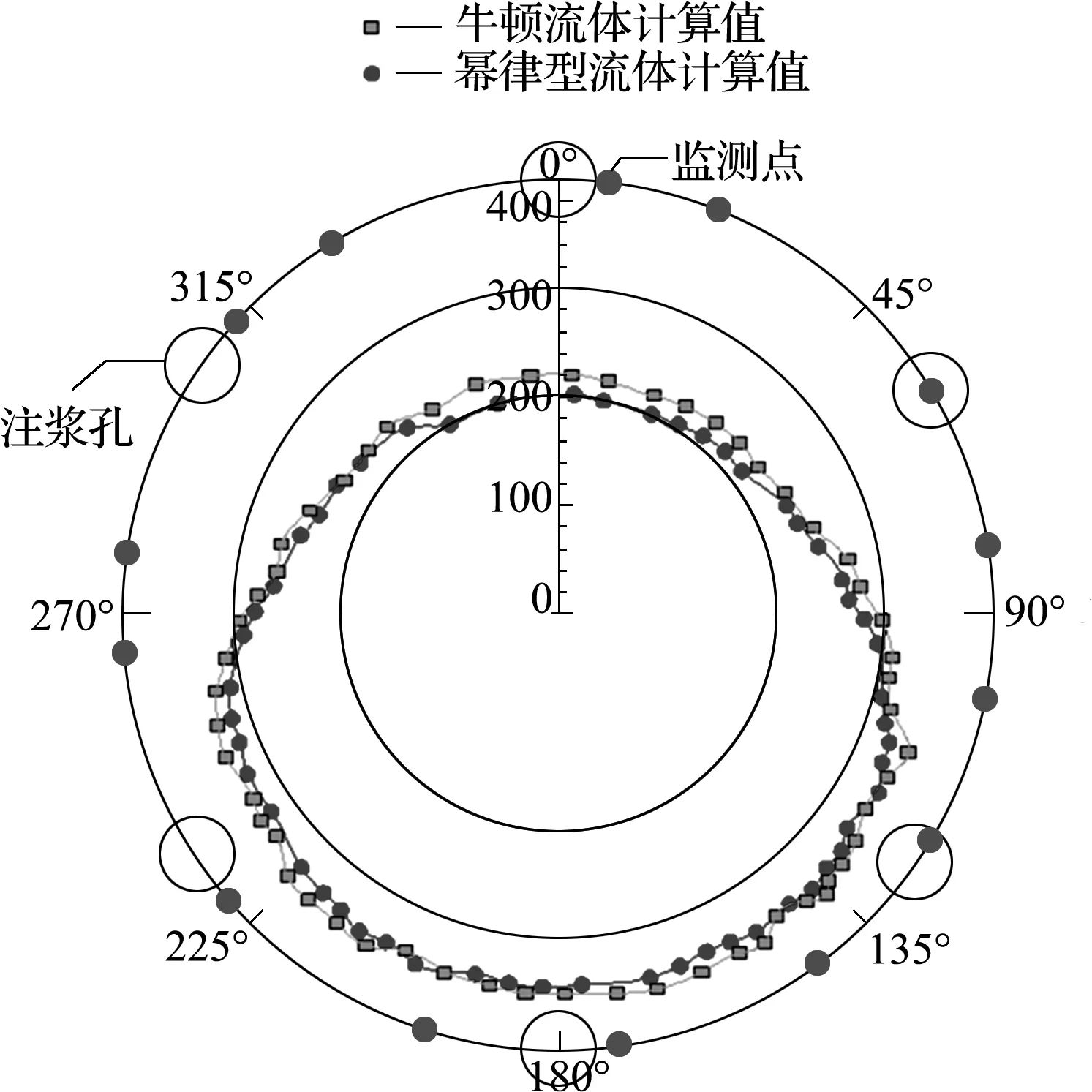
图6 牛顿浆液与幂律型浆液计算值对比
Fig.6 Comparison of calculated values between Newtonian and power-law grout
表2 不同水灰比的C和n值
Tab.2Candnvalues for different water-cement ratios

水灰比(W/C)稠度系数C流变系数n0.68.5320.1250.75.7320.100

图7 水灰比对扩散压力的影响
Fig.7 Influence of water-cement ratio on diffusion pressure
5 结 论
(1) 基于幂律型浆液扩散压力分布模型可反映盾尾注浆各个位置压力分布情况,得到相应的注浆压力计算式,并说明了参数意义及适用范围。
(2) 幂律型流体作为牛顿流体的推广,当稠度系数n=1时即为牛顿流体。环向压力扩散分布模型同样适用于牛顿流体;由于幂律型流体流动阻力大于牛顿流体,所以其环向扩散压力受流动阻力影响小于牛顿流体。
(3) 由于浆液自重,环形分布模型注浆孔向上注浆时表现为减压作用,向下注浆时表现为加压作用;压力环向分布断面呈现出上窄下宽的不规则环形;同一注浆孔幂律型浆液水灰比越大,浆液扩散压力越小,但其对浆液扩散压力影响不明显,注浆孔的注浆压力为主要影响因素。
