力-热载荷下双金属复合管的屈曲失效研究

郭奕蓉,张建勋,谭丁森,徐自力,秦庆华*

(1.西安交通大学 航天航空学院 机械结构强度与振动国家重点实验室，西安 710049；2.上海电气风电集团有限公司，上海 200235)

1 引 言

海洋油气管道工程是海洋石油开发中不可缺少的环节，在海上和海底的生产系统安装及运行过程中，由于深水超高压环境、输送压力和温度等复杂载荷的联合作用，复杂载荷下管道的力学研究显得尤为重要[1]。

使用双金属复合管是解决海洋高腐蚀环境相对安全和经济的途径之一。双金属复合管由外基管和内衬管组成，外基管一般为碳钢或低合金钢管，内衬管一般为不锈钢或耐蚀合金管。海底管道在服役使用过程中，会受到力-热载荷的联合作用，如埋地海底管道输送高温高压油气时，会受到不同程度轴向压力、内压及热载荷的联合作用；长悬跨段海底管道输送高温高压油气时，会受到弯曲载荷、内压及热载荷的联合作用。而且管道的工作压力越来越高，其设计温度接近100 ℃，有的甚至达到了150 ℃的高温[2]。长悬跨段海底复合管道会产生局部屈曲，最终导致整个管道失效。

双金属复合管有多种成型方法，最常用的是液压法。Vedeld等[3]对双金属复合管液压成型过程进行了理论分析和实验研究，得出外基管与内衬管的应力应变状态、液压力与两管间残余应力的计算公式。Yuan等[4]采用数值模拟，研究了双金属复合管的液压成型过程，得到复合管所受内压、残余环向应力与径向位移的关系。双金属复合管在服役使用过程中会受到多种荷载的联合作用而发生屈曲失效。Focke等[5]研究了双金属复合管在轴向压力作用下的屈曲失效，并分析了内衬管局部屈曲的影响因素。Di Vito等[6]通过实验和数值模拟研究了弯曲载荷作用下双金属复合管的屈曲，并分析了内压对内衬管屈曲的影响。文献[4,7-9]在考虑管道制造过程中残余应力及过盈接触应力影响的情况下，给内衬管引入初始几何缺陷和扰动，研究了弯曲载荷下双金属复合管的塑性分叉问题及弯曲和轴向压缩载荷下内衬管的屈曲失效。Vedeld等[10]采用理论分析方法对机械载荷-热载荷联合作用下双金属复合管的应力分布进行了研究，忽略制造过程中初始应力和应变的影响，得到了其应力场分布的解析表达式。

综上所述，目前大多数的研究是以双金属复合管的成型过程及单一力载荷下的变形和屈曲失效为主，对力-热载荷下双金属复合管的屈曲失效研究未见公开报道。因此，本文采用有限元方法对力-热载荷下双金属复合管的屈曲失效进行研究，对内衬管的初始几何缺陷进行了敏感性分析，同时研究了温度及内压两个参数对双金属复合管屈曲失效及变形的影响。

2 有限元模型

海底管道在输送高温高压油气的过程中会受到多种外部载荷的联合作用，如轴向压力、弯矩、内压及热载荷等。本文利用有限元软件ABAQUS(Version 6.13)，采用非线性屈曲分析方法分别对双金属复合管在轴向压力、内压和热载荷作用下及弯矩、内压和热载荷作用下的屈曲失效及变形机理进行分析。双金属复合管的有限元模型由外基管和内衬管两部分组成。考虑到复合管沿轴向和径向的对称性，为了减少计算量，仅建立整体复合管的1/4模型进行计算，如图1所示。

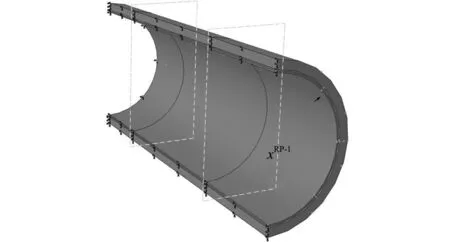
图1 有限元模型(1/4模型)

Fig.1 Finite element model (1/4 model)

选取双金属复合管的管长L=1412 mm，外基管的材料一般为X-65钢或X-75钢，本文选用X-75钢，内衬管的材料选用SS -304不锈钢。材料本构模型采用龙伯格奥斯古德(Ramberg-Osgood)模型：

(1)

式中E为材料的初始弹性模量，σy为屈服强度，n为应力指数。具体的几何及材料参数设置列入 表1[4]。

热载荷作用下两种材料的弹性模量E、屈服强度σy、热传导系数TC和热膨胀系数TE均随温度变化，对应数值分别列入表2～表5[11]。

为了考虑内衬管初始几何缺陷的影响，假定内衬管初始几何缺陷是轴对称与非轴对称缺陷的混合模式，其表达式为[4]

(2)

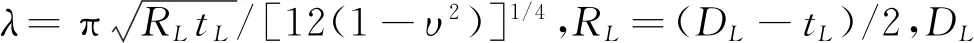
内外管均采用ABAQUS/Standard的C3D8T单元进行计算，且内外管网格划分均一致。沿径向有4个单元，沿环向有140个单元，沿轴向网格的疏密不同,在0 mm ≤x≤146 mm范围内，有22个单元；在146 mm ≤x≤496 mm范围内，有 27个 单元；在496 mm ≤x≤706 mm范围内，有11个单元。经过验证，网格类型和数量均符合要求，无异常网格。模型的网格划分如图3所示。内外管之间的接触属性为自动面面接触，采用有限滑移方式，未考虑内外两管之间摩擦力的影响，热传导系数为 1220 W/(mm2℃)。

图2 含初始几何缺陷的内衬管

Fig.2 Liner with initial geometric imperfection

表1 复合管几何及材料参数Tab.1 Geometric and material parameters of lined pipe

表2 弹性模量随温度的变化

Tab.2 Elasticity modulus by temperature

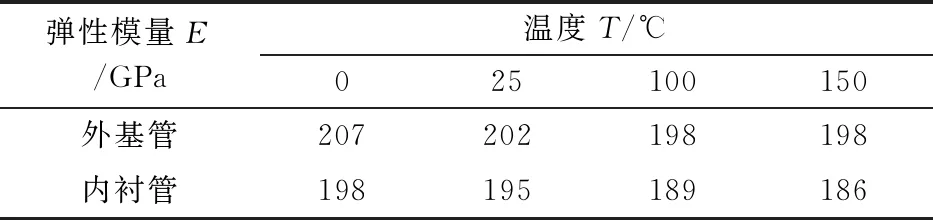
弹性模量E/GPa温度T/℃025100150外基管207202198198内衬管198195189186

表3 屈服强度随温度的变化

Tab.3 Yield strength by temperature

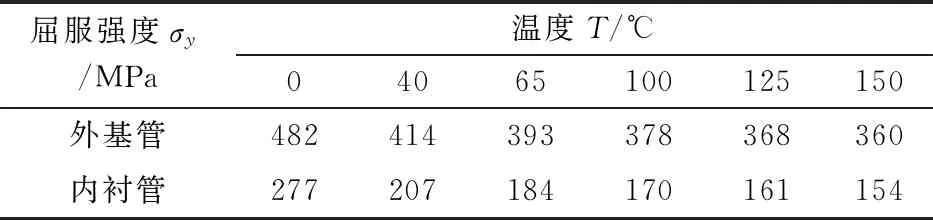
屈服强度σy/MPa温度T/℃04065100125150外基管482414393378368360内衬管277207184170161154

表4 热传导系数随温度的变化

Tab.4 Thermal conductivity by temperature

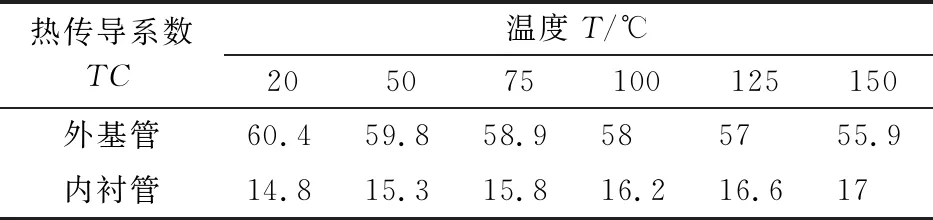
热传导系数TC温度T/℃205075100125150外基管60.459.858.9585755.9内衬管14.815.315.816.216.617

表5 热膨胀系数随温度的变化

Tab.5 Thermal expansion coefficient by temperature

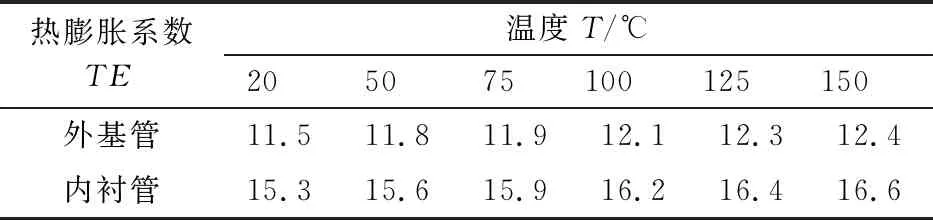
热膨胀系数TE温度T/℃205075100 125 150 外基管11.511.811.912.112.312.4内衬管15.315.615.916.216.416.6

在双金属复合管的制造过程中，外基管仅发生弹性变形，而内衬管发生一定程度的塑性变形，卸载后通过机械结合形成双金属复合管，但内外两管均有残余应力存在。本文选取双金属复合管液压复合成型过程进行数值模拟[4]，如图4所示。在内衬管的内壁施加均布压力，使内衬管沿径向向外扩张，直到与外基管的内壁接触，并随外基管继续扩张，直至均布压力卸载，最终得到通过机械复合的双金属复合管。

海底双金属复合管在输送高温高压油气的过程中会受到轴向压力、弯矩、内压及热载荷等作用，本文主要针对海底双金属复合管在输送高温高压油气过程中的两种工况进行分析。一是轴向压力、内压和热载荷作用；二是弯矩、内压和热载荷作用。

计算模型的边界条件的设置如图5所示。工况1涉及轴向压力F的加载，通过控制复合管端面节点的轴向位移δx来实现；工况2涉及弯矩M的加载,选择复合管端面圆心作为一参考点，同时与端面上的节点形成动态耦合约束，通过对该参考点施加转角θ来实现。

图3 网格划分

Fig.3 Meshing

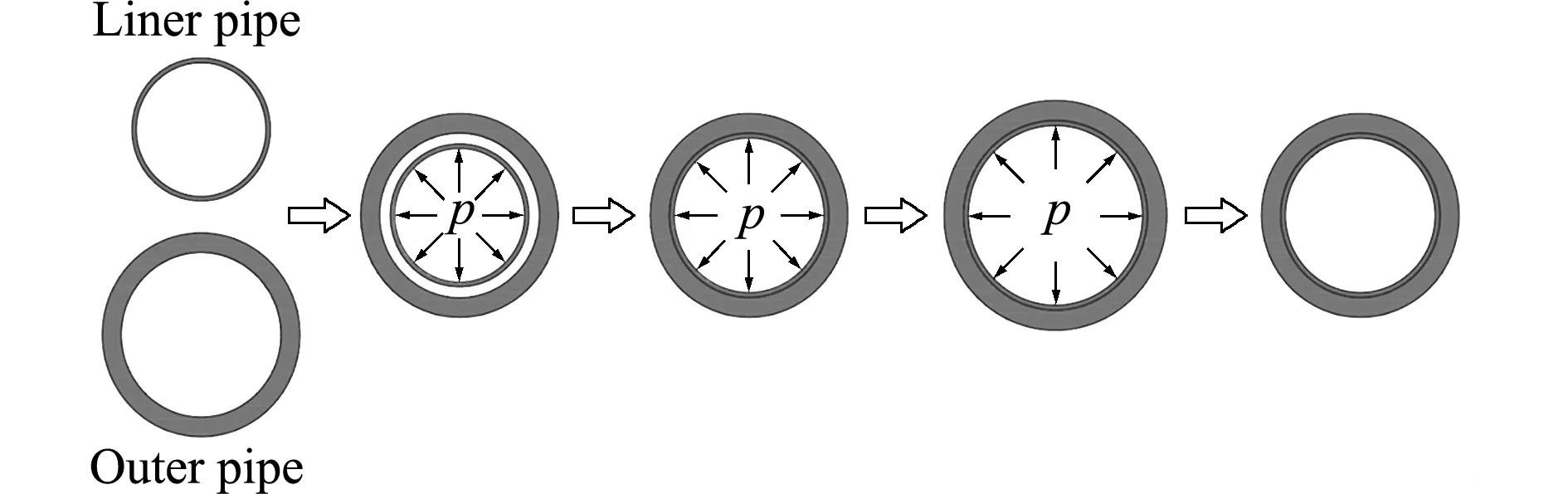
图4 液压成型法

Fig.4 Hydro -forming of lined pipe

通过对内衬管内壁施加均布载荷pi实现内压的加载；通过设置复合管的外环境温度TS和复合管内运输的油气温度TL实现热载荷的加载,且两种工况的载荷均同时加载。一般内充压力介质的范围是0 MPa～5.8 MPa[12]，本文取pi= 0.5 MPa，复合管外环境温度的范围是-2 ℃～30 ℃，本文取TS=10 ℃，复合管内运输的油气温度的范围是100 ℃～150 ℃[13]，除非特别说明，内充介质的温度选取TL=150 ℃。对于工况1，轴向位移δx=40 mm，如图6所示；对于工况2，转角θ=0.25 rad，如图7所示。

由于双金属复合管的液压成型过程导致外基管与内衬管形成过盈配合，两管间出现了残余应力，而残余应力的存在对双金属复合管的力学行为有重要影响。因此，需要通过定义一个初始状态场，将双金属复合管液压成型后的状态和网格一并导入，如图8所示，即可完成复合管液压成型与复合管加载过程的数据传递。

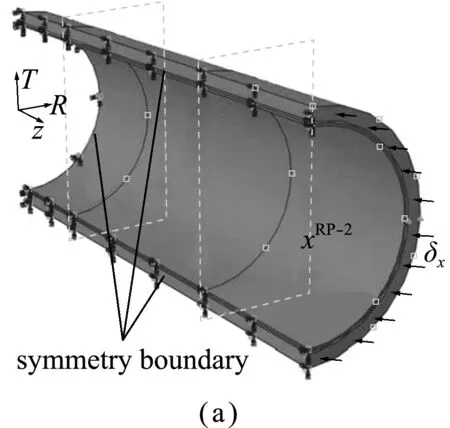
图5 两种载荷下边界条件

Fig.5 Boundary conditions under two loading cases

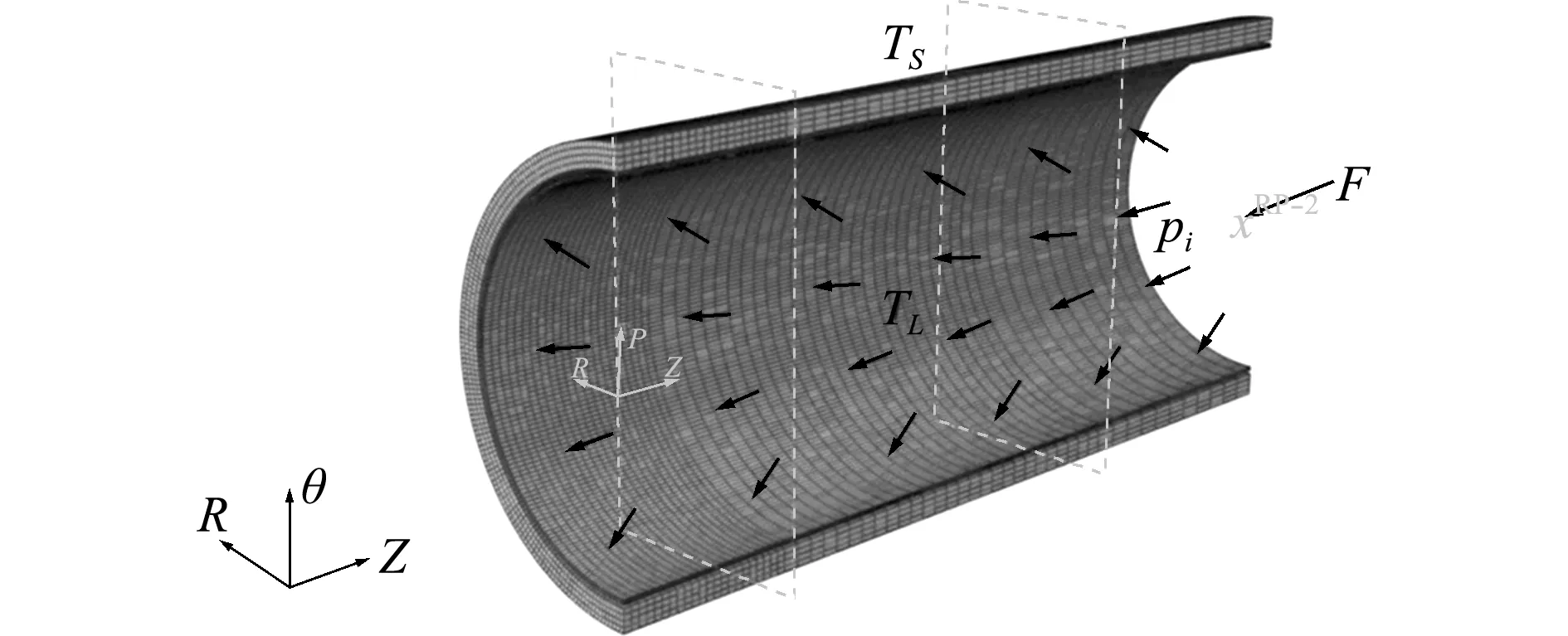
图6 轴向压力、内压及热载荷作用

Fig.6 Combined axial pressure,internal pressure and thermal loadings

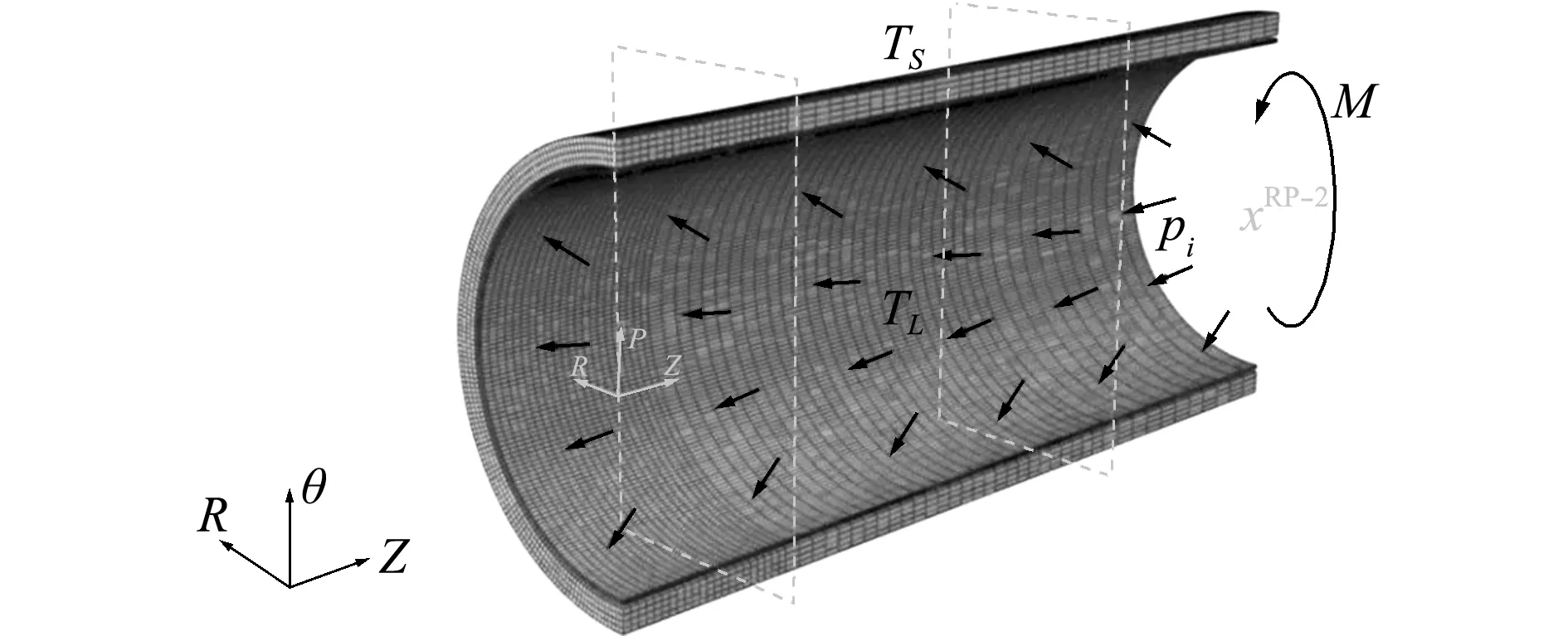
图7 弯矩、内压及热载荷作用

Fig.7 Combined bending,internal pressure and thermal loadings

3 结果与讨论

3.1 轴向压力、内压及热载荷联合作用

图9所示为内外管受到的轴向压力与轴向位移关系对比曲线，其中，Fo=σoA为外基管受到的轴向屈服压力，其中σo为外基管屈服强度，A为外基管横截面积。可以看出，当复合管受到轴向压力、内压及热载荷作用时，初始段的轴向压力均随着轴向位移近似呈线性增加，对应的复合管发生了弹性变形。随着压缩变形的增加，复合管发生塑性屈服，外基管的轴向压力随着轴向位移近似呈线性增加，而内衬管的轴向压力几乎保持不变，说明复合管未发生明显屈曲。

图10为内衬管变形过程的应力云纹图。可以看出，内衬管同样只沿轴向发生了压缩，并未出现明显的局部屈曲。

为了研究热载荷对双金属复合管的影响，进一步对复合管在轴向压力及内压联合作用下的屈曲进行数值模拟，并将计算结果与上述考虑热载荷作用的结果进行了比较，如图11所示。可以看出，对于复合管仅受轴向压力及内压作用，当内衬管受到的轴向压力达到峰值时，随着轴向位移的增加，内衬管受到的轴向压力开始减小，内衬管的刚度急剧降低，说明此时内衬管发生了屈曲。当热载荷存在时，内衬管的轴向压力基本没有变化，说明内衬管未发生明显的屈曲，这可能是热载荷的存在使得材料发生软化，从而抑制了内衬管屈曲的发生。

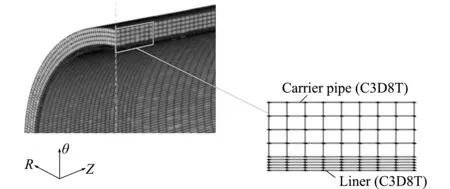
图8 初始状态导入时的单元分布

Fig.8 Element distribution imported at the initial state

图9 内外管受到的轴向压力-轴向位移关系对比

Fig.9 Comparison of axial pressure -axial displacement curves of steel and liner pipes

3.2 弯矩、内压及热载荷联合作用

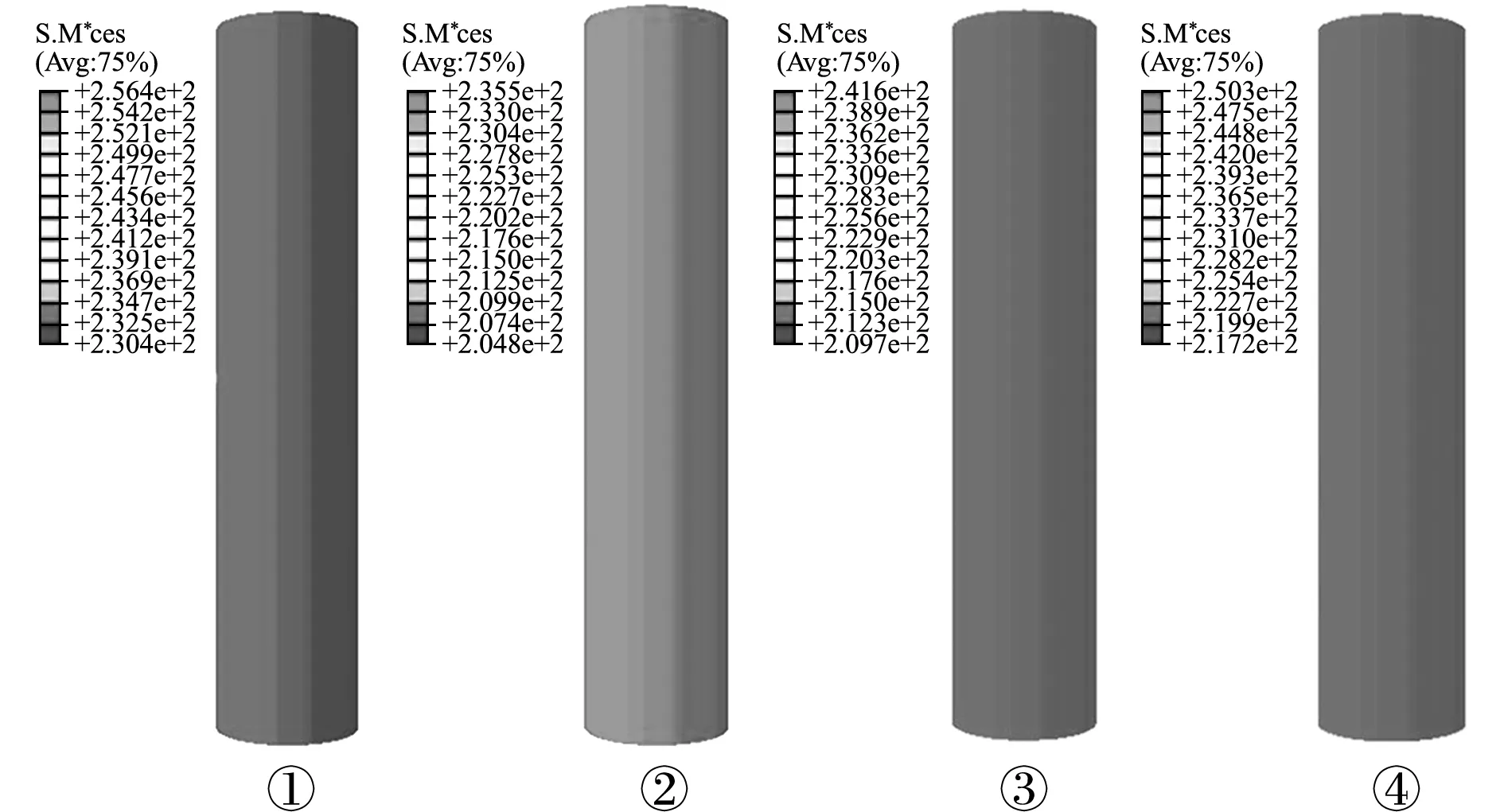
图10 内衬管变形过程的应力云纹图

Fig.10 Sequences of liner deformed configurations

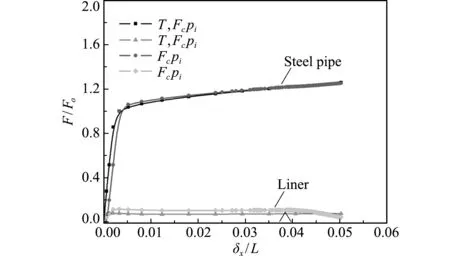
图11 热载荷的影响

Fig.11 Effect of thermal loading

4 缺陷敏感性

为了分析缺陷对复合管屈曲失效的影响，假定保持环向波数m不变，改变轴对称缺陷幅值ωo和非轴对称缺陷幅值ωm，其中，环向波数m=8。缺陷幅值取2组值，分别为ωo=0.01 mm和ωm=0.06 mm；ωo=0.1 mm和ωm=0.1 mm。

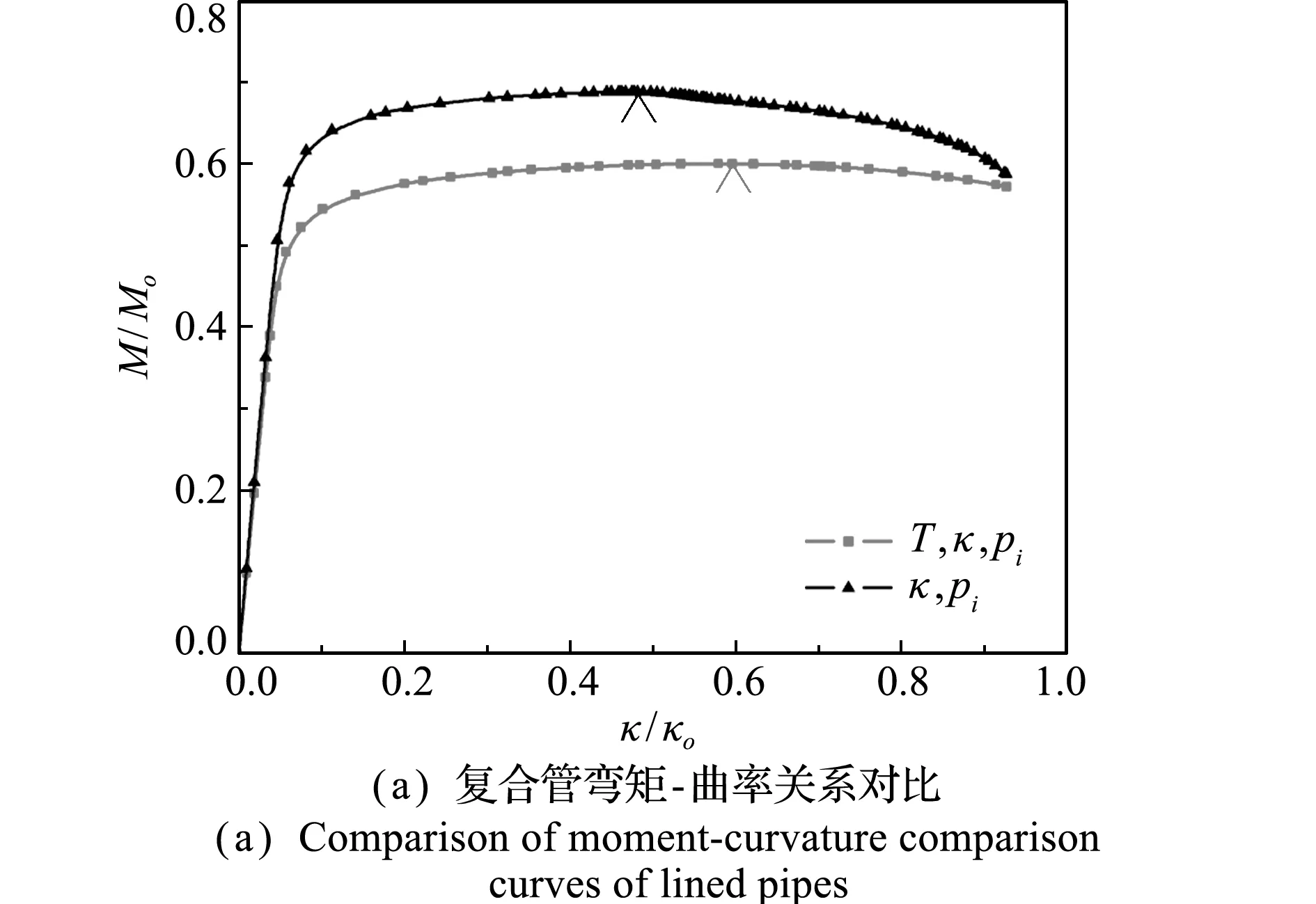
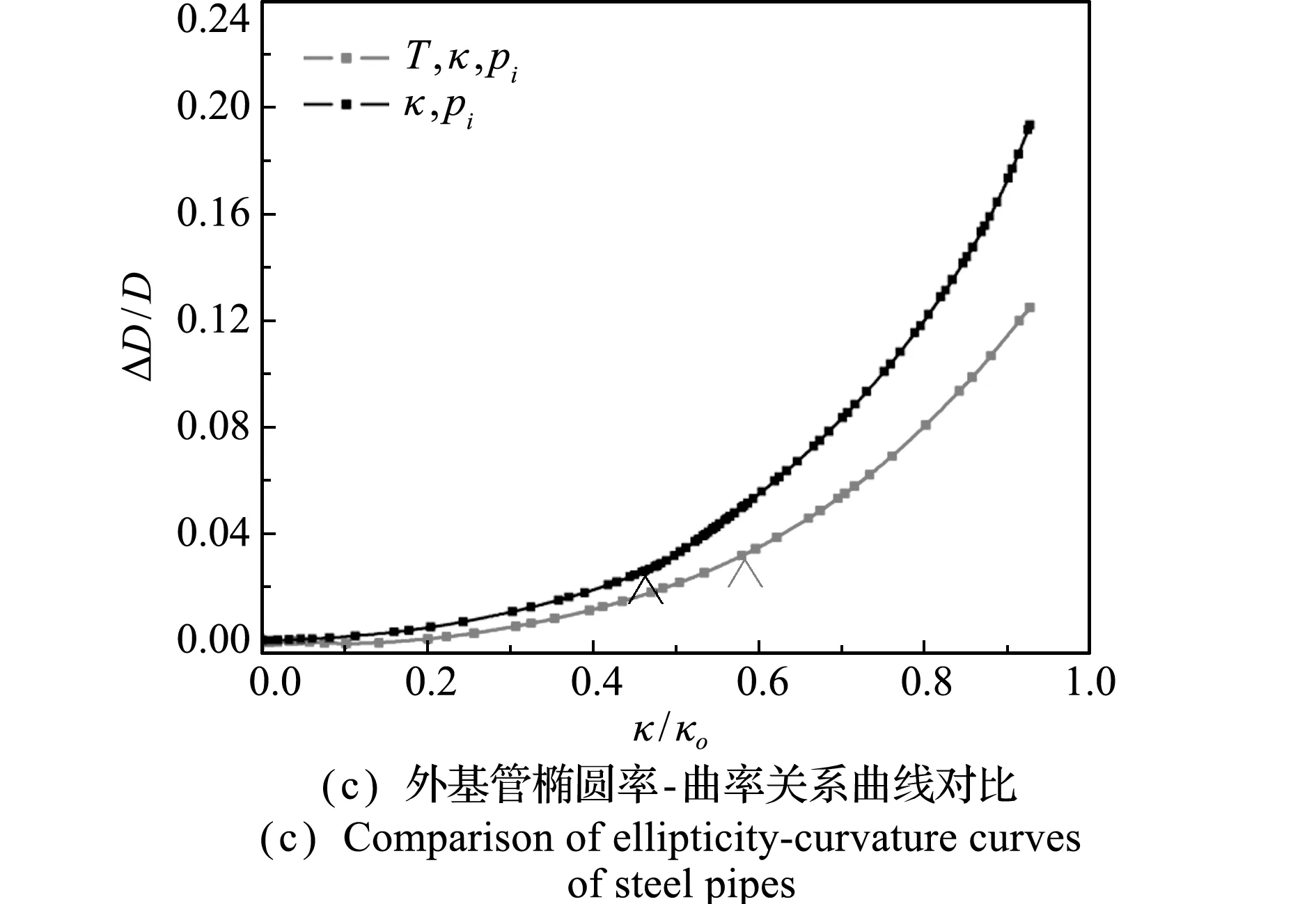
图12 热载荷的影响

Fig.12 Effect of thermal loading

4.1 轴向压力、内压及热载荷联合作用

图14给出了缺陷幅值对轴向压力、内压及热载荷联合作用下双金属复合管轴向力的影响。可以看出，增大内衬管的缺陷幅值，对内衬管和外基管受到的轴向压力影响很小。

4.2 弯矩、内压及热载荷联合作用

图15给出了缺陷幅值对弯矩、内压及热载荷联合作用下双金属复合管弯矩、褶皱幅值和椭圆率的影响。可以看出，内衬管的缺陷幅值增大，复合管弯矩达到最大值对应的曲率减小，外基管的椭圆率增大。

5 参数分析

5.1 轴向压力、内压及热载荷联合作用

5.1.1 温度影响

假定管外环境温度TS和内压pi保持不变，改变管内介质温度TL，其中，管外环境温度TS=10 ℃，内压pi=0.5 MPa，管内介质温度TL分别取80 ℃和150 ℃。从图16可以看出，在轴向压力、内压及温度联合作用下，管内介质温度的变化对内衬管和外基管承载能力影响不大，且内衬管的轴向压力基本没有变化。说明两种温度工况下内衬管均未发生明显屈曲。

图13 内衬管变形过程的应力云纹图

Fig.13 Sequences of liner deformed configurations

图14 缺陷幅值的影响

Fig.14 Effect of imperfection amplitude

5.1.2 内压影响

假定管外环境温度TS和管内介质温度TL保持不变，改变内压pi，其中，管外环境温度TS=10 ℃，管内介质温度TL=150 ℃，内压pi分别取0.25 MPa和0.5 MPa。从图17可以看出，在轴向压力、内压及温度联合作用下，减小内压对内衬管和外基管承载能力影响不大，且内衬管的轴向压力基本没有变化。说明两种内压工况下内衬管均未发生明显屈曲。

5.2 弯矩、内压及热载荷联合作用

5.2.1 温度影响

温度及内压设定同5.1.1节。图18结果表明，在弯矩、内压及热载荷联合作用下，复合管内介质温度降低，复合管弯矩达到最大值对应的曲率减小，弯曲承载能力增大，外基管的椭圆率也增大。

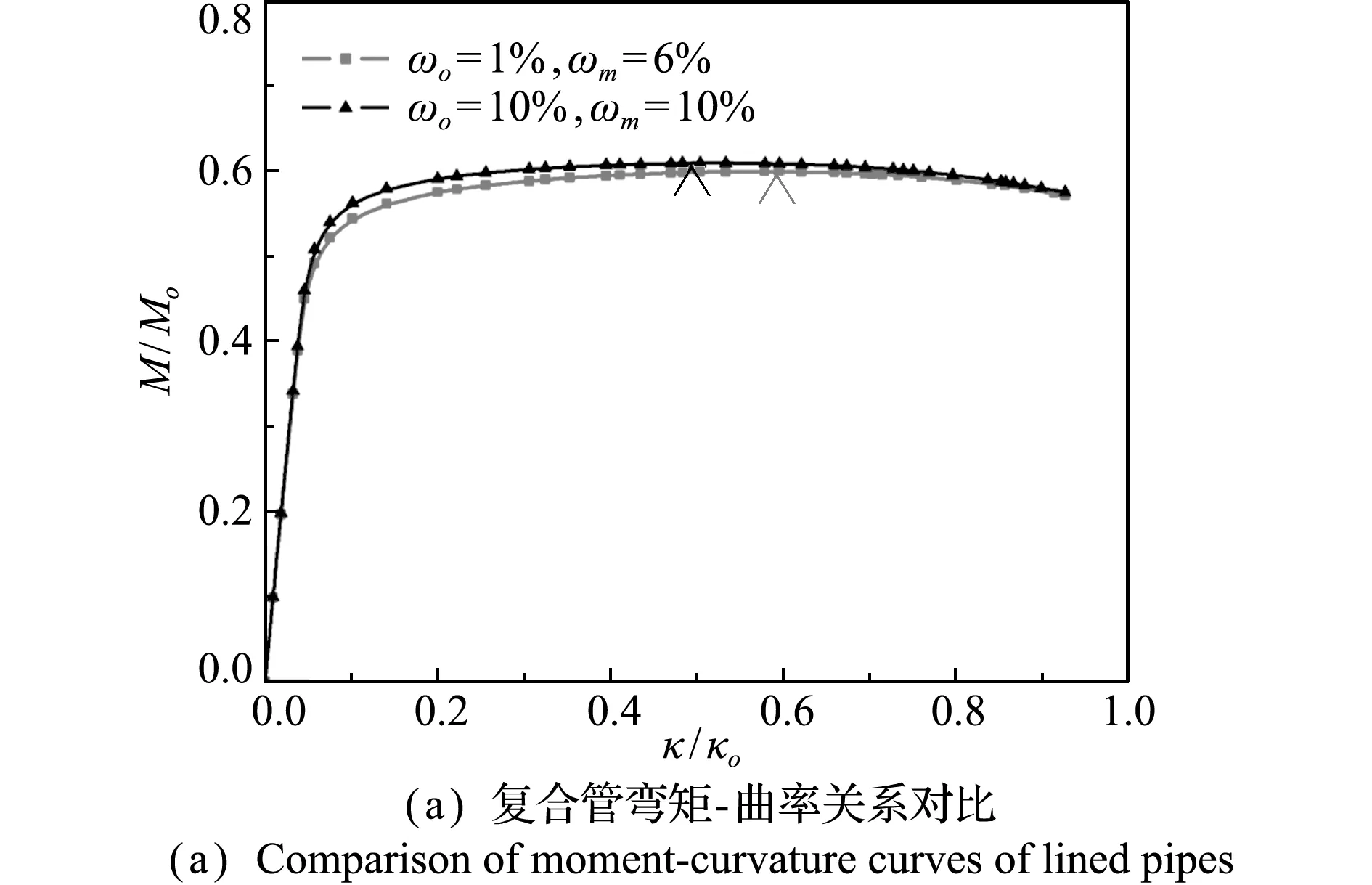
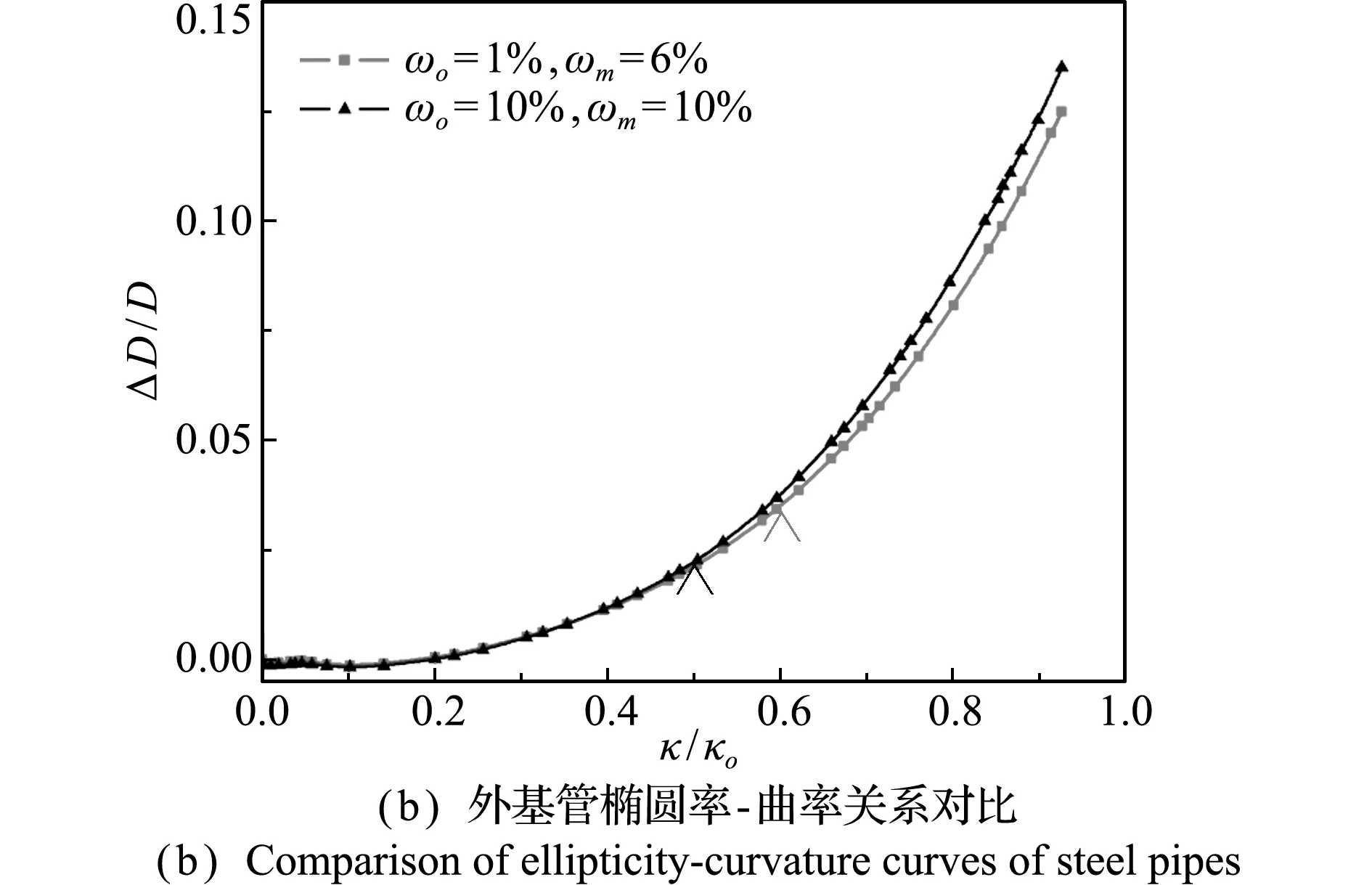
图15 缺陷幅值的影响

Fig.15 Effect of imperfection amplitude

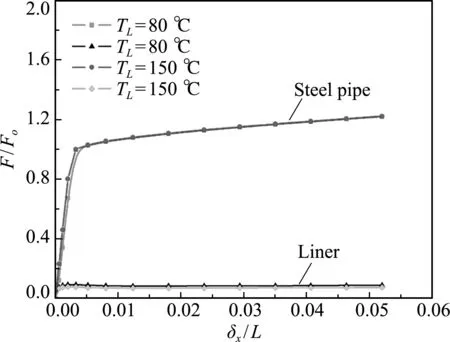
图16 温度的影响

Fig.16 Effect of temperature

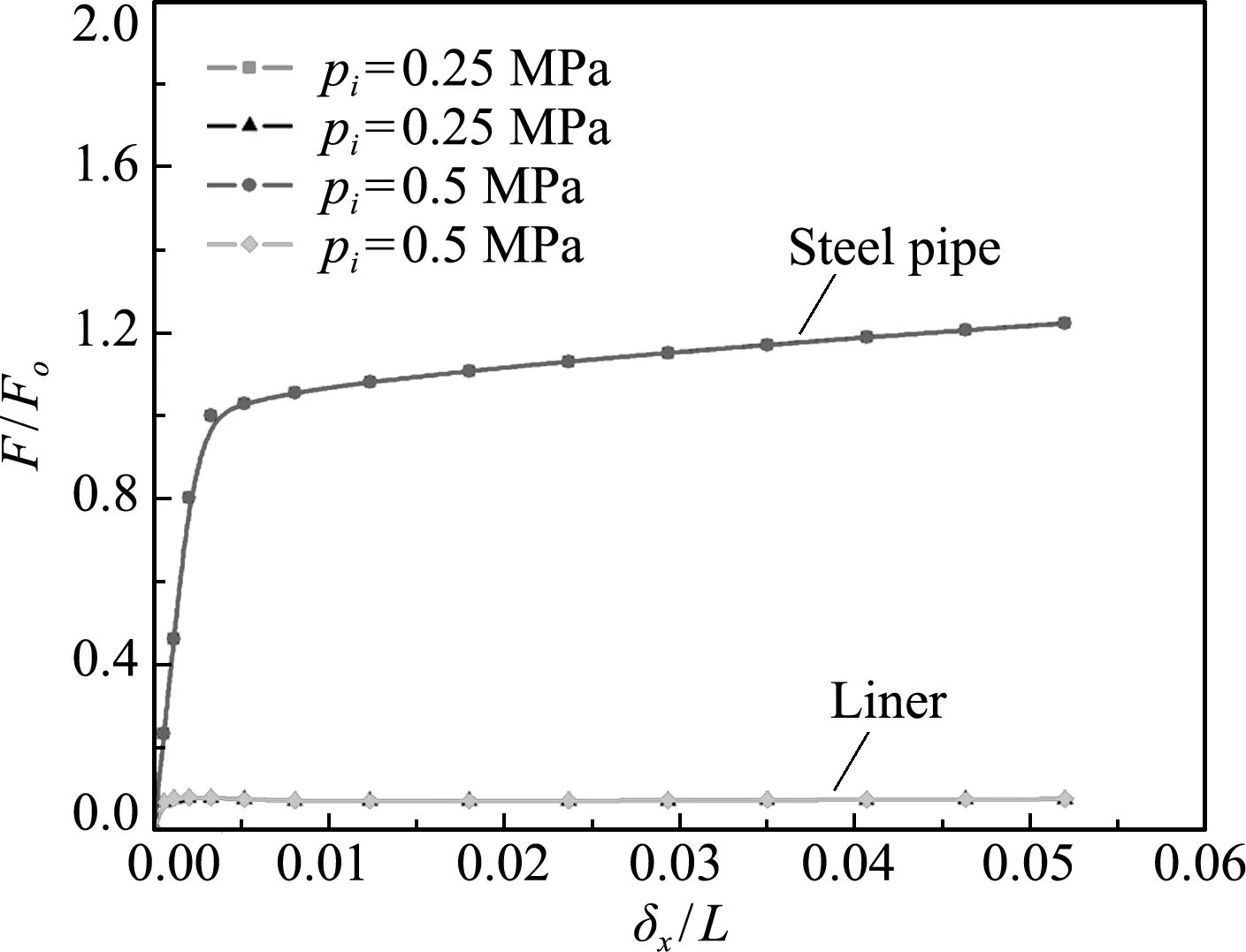
图17 内压的影响

Fig.17 Effect of internal pressures

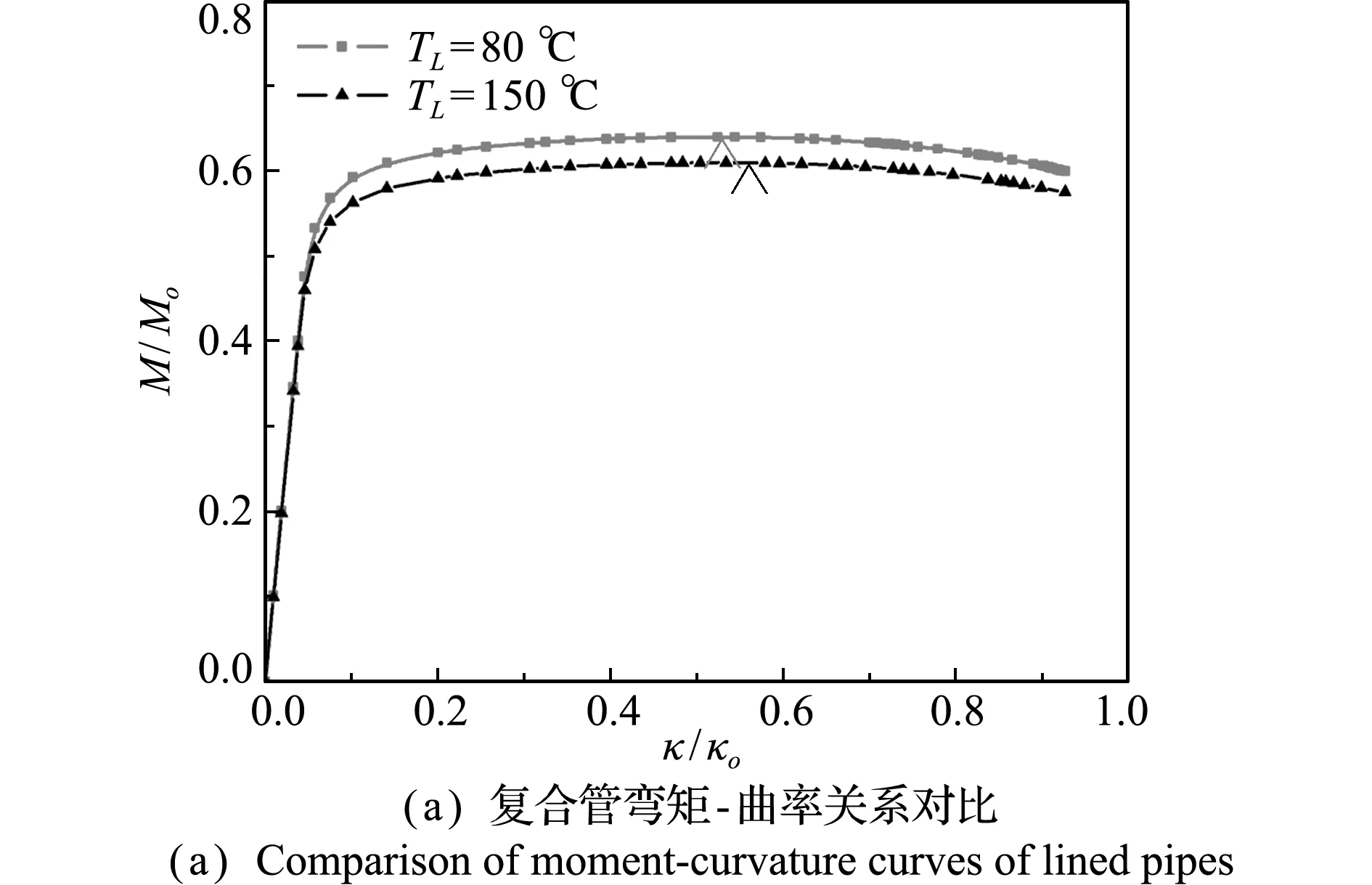
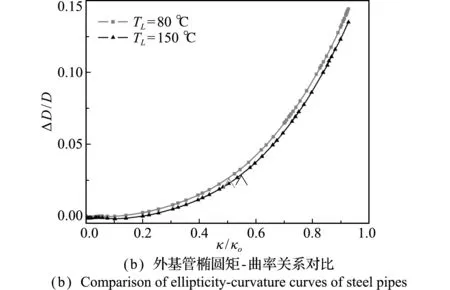
图18 温度的影响

Fig.18 Effect of temperature

5.2.2 内压影响

温度及内压设定同5.1.2节。图19结果表明，在弯矩、内压及热载荷联合作用下，内压变化对复合管的弯曲承载能力和外基管的椭圆率影响较小。

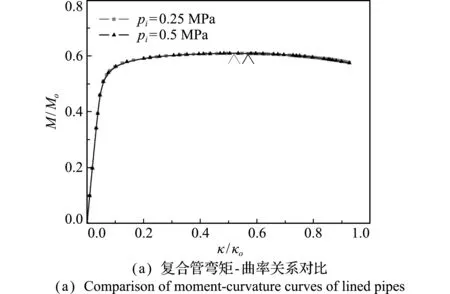
图19 内压的影响

Fig.19 Effect of internal pressures

6 结 论

(1) 复合管在受到轴压、内压及热载荷作用时，内衬管未发生明显屈曲，这可能是由于双金属复合管受到热载荷作用时材料发生软化，抑制了内衬管的屈曲。

(2) 复合管在受到弯矩、内压及热载荷作用时，热载荷致使材料发生软化，抑制了内衬管的屈曲，但降低了复合管的弯曲承载能力；内衬管的缺陷幅值增大，复合管弯矩达到最大值对应的曲率减小，外基管的椭圆率增大；复合管内介质温度降低，复合管弯矩达到最大值对应的曲率减小，弯曲承载能力增大，外基管的椭圆率也增大；内压变化对复合管的弯曲承载能力和外基管的椭圆率影响较小。