利用重叠分离机构进行纸张分离的纸张动态分析
2020-05-22柴德望
柴德望,丁 千*,张 泉
(1.天津大学 力学系,天津 300350;2.恒银金融科技股份有限公司博士后科研工作站,天津 300308)
1 引 言
在印刷和金融自助类设备中(如打印机、复印机和自动存取款机等),纸张类媒介传输系统作为关键的子系统,通常由滚轮系统组成,在各个模块通道中完成对纸张媒介的传输[1]。在ATM机中,重叠分离机构用于纸张的快速准确分离,是设备运行的重要步骤。当纸张进入重叠夹缝,变形力和摩擦力作用在纸张接触表面使其分离,但由于摩擦条件的变化和纸张处于不同的情形(折角、缺角和褶皱等),传送失效和重张的现象在分离设备中时有发生[2-4]。
在对纸张变形力的分析中,纸张受到交错轮压力作用,通常简化为弹性梁模型[2,4,5];一些学者[6-8]把纸张简化成弹簧-梁-质量块模型分析纸张行进过程出现的卷曲变形和堆叠卡纸等现象;陈雪峰等[9]利用不同的有限元法计算纸张的静态特性,对比发现等参元模型相对计算量少且精度高;鲍照等[10]考虑了送纸胶轮的形变,推导出纸张运动方程,并利用Recurdyn软件分析送纸机构,分析卡纸现象及影响因素;还有一些研究[11-14]采用库伦摩擦力的修正模型,分析结构参数对纸张运动的影响。这些分析方法都能有效指导设计,但鲜有考虑纸张在通过重叠分离机构过程中变形力的变化因素。
本文采用弹性梁模型计算纸币所受变形力,考虑了纸币通过重叠分离机构时变形力的变化,利用修正的摩擦力模型计算纸币通过分离机构的动态特性,并分析了影响因素,可为结构设计提供参考。
2 重叠分离机构原理
纸张存储形式可以是水平形式或竖直形式[15]。竖直存储的重叠分离机构如图1所示,包括3组轮(挖钞轮、送钞轮和剥离轮)和推板。送钞轮和剥离轮在轴向排列上有偏移,在径向方向上有重叠。当推板移动时,压力首先产生于固定挖钞轮机构的弹簧。托板与重叠机构的竖向距离为一个挖钞冲程h0,挖钞轮高摩钞区部分A的弧长大于挖钞冲程,使得钞票受摩擦力的作用能够顺利到达重叠分离机构。当高摩擦部分A接触第一张纸时,纸张开始通过挖钞轮和送钞轮的旋转陆续带出,一旦纸张进入重叠夹缝,就会产生波变形,产生变形力。在夹缝区纸张的有效变形宽度为b。在挖钞轮和送钞轮的传输力与固定的剥离轮抵抗力的共同作用下,实现纸张间的分离[4]。
3 纸币剥离模型分析
纸币在挖钞轮的作用下经过挖钞冲程进入重叠分离区,此时纸币的受力如图2所示,其中图2(a)为单张纸币情形,图2(b)为两张纸币的情形(连张情形)。在纸币的分离过程中,假设纸币之间产生的运动为刚体之间的滑动,忽略摩擦变形。为了简化纸张与滚轮的接触变形问题,由于重叠分离机构中送钞轮与剥离轮的错位,橡胶层的变形量相对较小,本文未考虑橡胶层变形量对纸币运动的影响。
为分析纸币分离过程,首先根据图2建立分离机构的力学模型。其中,送钞轮和剥离轮与纸币之间的压力由纸币所受变形力提供,并随着纸币进入分离机构位移的大小而发生变化。假设纸币之间产生的运动为刚体之间的滑动,忽略摩擦变形,对分离机构的力学模型进行受力分析,建立单张纸币传送过程中纸币的动力学方程:
(1)
摩擦力采用修正的库伦摩擦力模型[16,17],式中各个接触表面的摩擦力为
(2)
各接触表面的相对滑动速度为
(3)
令纸币的质量为m,则可得
(4)
式中Jf和Jg分别是送钞轮和剥离轮的转动惯量;v是纸币的前进速度;m为纸币的质量;ωf和ωg分别为送钞轮和剥离轮的角速度;ff s和fg s分别为送钞轮和剥离轮与纸币的摩擦力,本文选择常数C= 10 m/s;W为纸币所受变形力;μf s和μg s分别为送钞轮和剥离轮与纸币之间的动摩擦系数;Rf和Rg分别为送钞轮和剥离轮的半径;M和T分别是送钞轮和剥离轮的转矩。
由式(3,4)计算可得纸币加速度为
(5)
根据式(1)可知,送钞轮和剥离轮的角速度分别为
(6)
代入各参数,可算出t时刻纸币的加速度为
(7)
速度和位移为
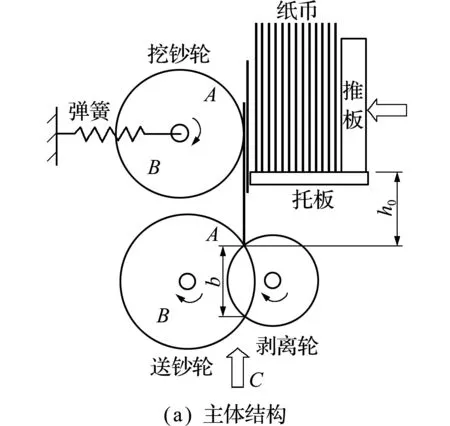
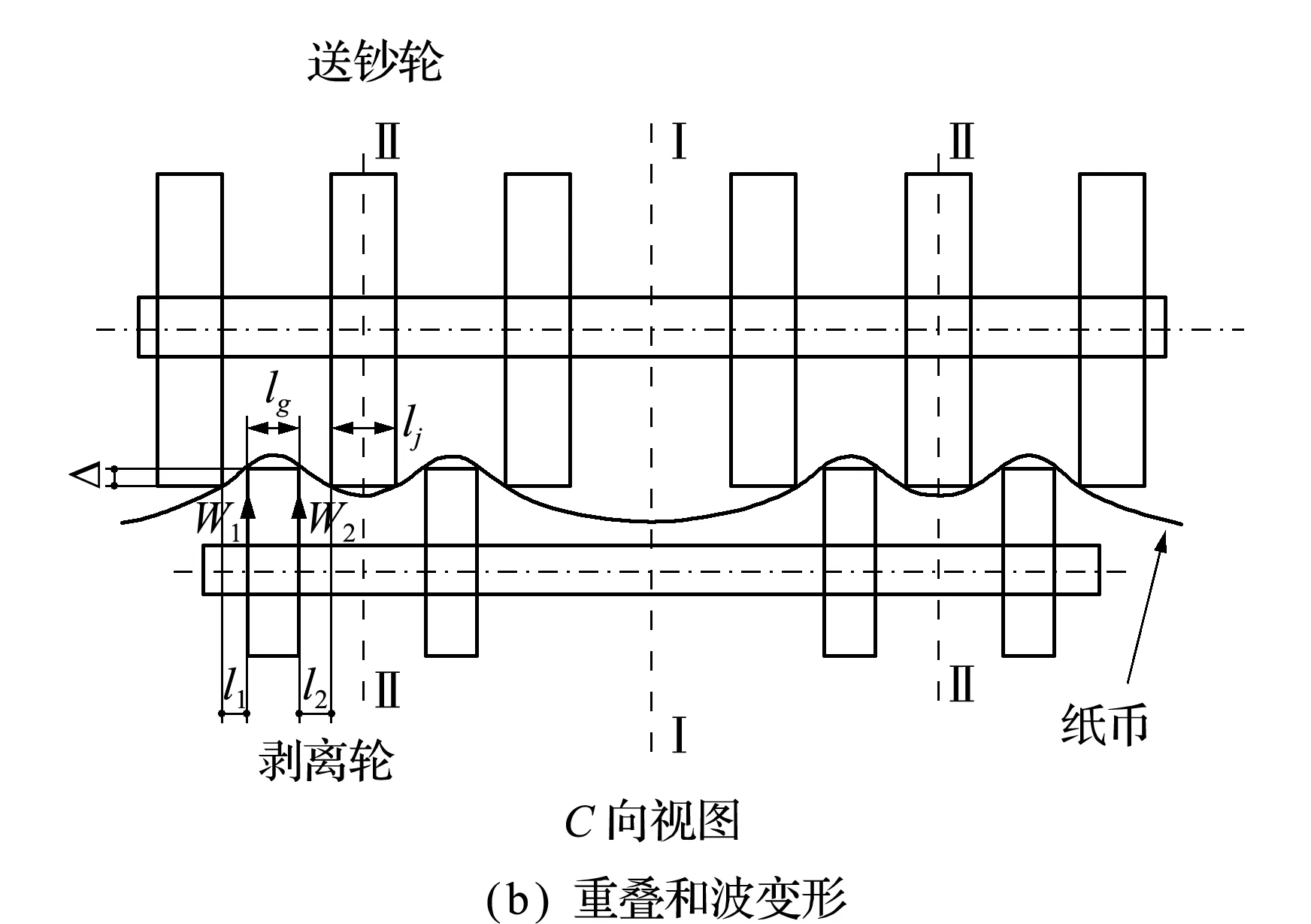
图1 分离机理
Fig.1 Separation mechanism
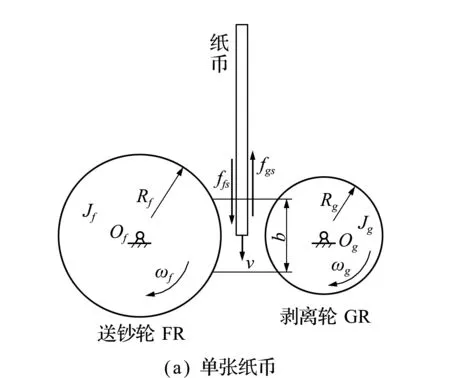
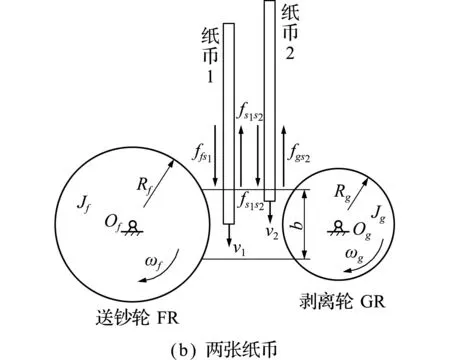
图2 分离力分析
Fig.2 Analysis of separation forces
(8)
(9)
同理,根据图2(b),建立两张纸币分离过程中纸币的动力学方程为
(10)
(11)
式(10,11)的各摩擦力亦采用修正的库伦摩擦力模型,各个接触表面的摩擦力为
(12)
各个接触表面的相对滑动速度为
(13)
式中Jf和Jg分别是送钞轮和剥离轮的转动惯量;v1和v2是第一张和第二张纸币的前进速度;m为纸币的质量;ωf和ωg分别为送钞轮和剥离轮的角速度;ffs 1,fs 1s 2和fg s2为各接触表面的摩擦力;μf s,μs 1s 2和μg s分别为送钞轮与纸币之间、纸币之间以及纸币与剥离轮之间的动摩擦系数;Rf和Rg分别为送钞轮和剥离轮的半径;M和T分别是送钞轮和剥离轮的转矩。
同理可得第一张和第二张纸币的加速度表达式为
(14)
则第一张纸币和第二张纸币t时刻的速度分别为
(15)
第一张和第二张纸币t时刻的位移分别为
(16)
4 纸币所受变形力随时间的变化
滑移在纸币传输中受多种因素影响,包括滚轮与纸币的摩擦系数、滚轮的角速度以及滚轮之间与纸币的正向力。重叠分离机构滚轮对与纸币的正向力由纸币变形力提供。根据三弯矩定理及结构对称性可以求出重叠分离机构中纸币变形力为[2,4]
W=4(W1+W2)
(17)
式中W1和W2为剥离轮对纸币的压力,分别为
(18)
(19)
其中,E为纸币弹性模量,I=bh3/12为纸币的几何惯性矩,b为纸币的有效变形宽度,h为纸币的厚度,l1和l2为送钞轮与剥离轮的左右轮间距,lf和lg为送钞轮和剥离轮的厚度。纸币受挖钞轮的作用开始从o点进入重叠分离机构至完全脱离重叠机构的过程中,纸币受到实际影响的有效变形宽度b和重叠量Δ随着纸币位移而变化,其几何关系如图3所示。
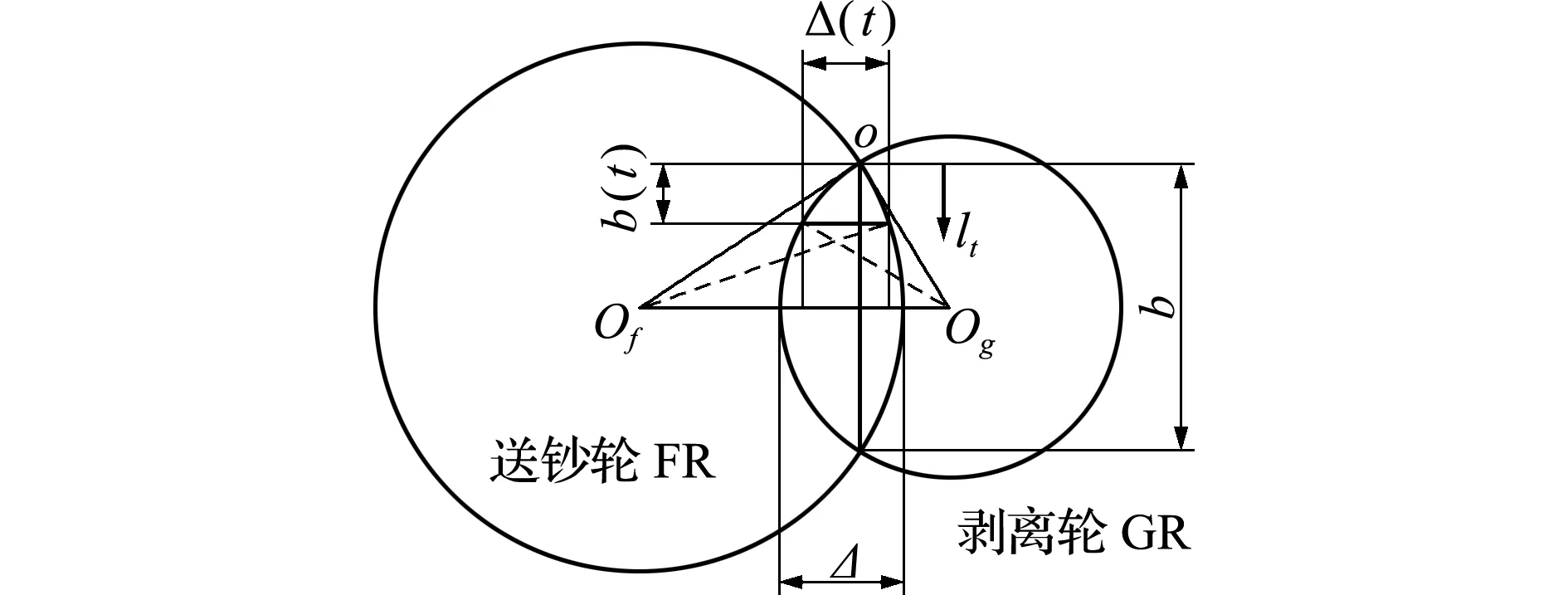
图3 纸币进入分离机构的几何关系
Fig.3 Geometrical relationship while the paper is being separated
随着纸币进入重叠分离机构位移lt的变化,在求式(17)变形力时,纸币受到实际影响的b和Δ用式(20,21)进行计算,
(20)
Δ(t)=
(21)
式中bs为纸币宽度,dfg为送钞轮与剥离轮的圆心距,若重叠分离机构的交叠量Δ固定,df g可由式(22)确定,重叠分离机构的有效宽度b可由式(23)确定。
df g=Rf+Rg-Δ
(22)
(23)
5 主要结构参数的影响
参考图1(b),某ATM机重叠分离机构的主要参数为[4]l1=1.24 mm,l2=1.08 mm,lg=3.88 mm,lf=2.2 mm,Δ=0.5 mm;挖钞轮、送钞轮和剥离轮的半径分别为Rp=Rf=20 mm,Rg=12 mm;送钞轮和剥离轮都是包胶轮结构,内层是铝合金,外圈是聚氨酯材料,在proE模型中可直接获得mf=95.8 g,mg=11.38 g,转动惯量Jf=17.22 kg·mm2,Jg=9.1 kg·mm2,剥离轮的转矩T=2 N·mm;有效变形宽度b可根据式(22,23)得到b=5.4 mm;纸币的弹性模量E=2250 N/mm2,长度l=155 mm,宽度bs=77 mm,厚度h=0.1 mm,质量m=1.15 g;摩擦系数分别为μf s=0.9,μs 1s 2=0.2,μg s=0.4。
初始条件为纸币到达重叠分离机构的速度略小于挖钞速度,令其为v0=1.79 m/s,纸币的初始加速度为a0=0 m/s2,送钞轮的线速度为vf=1.8 m/s。
当单张纸币通过分离机构时,变形力W(t),b(t)和Δ(t)随时间t的变化如图4所示。纸币开始进入重叠分离机构,b(t)逐渐增大,增大至重叠分离机构有效宽度b时纸币受完全夹持,此时b(t)为最大值5.4 mm,并保持到纸币尾端到达起始点o,再随着纸币的进一步离开逐渐减小至0;Δ(t)也逐渐增大,当对应纸币位移为b/2时达到最大值0.5 mm,并保持到纸币尾端到达重叠分离机构的b/2处时再逐渐减小至0;变形力W(t)也随着纸币的进入而先增大后减小,当纸币受完全夹持时变形力最大。此结果符合纸币通过重叠分离机构的运动规律,并在b(t)=5.4 mm,Δ(t)=0.5 mm时,W(t)=0.9 N,与文献[4]数据吻合,可用于纸币运动分析计算。
5.1 交叠量Δ对进纸阶段动态特性的影响(单/双张)
若重叠分离机构相关轮的尺寸固定,可微调送钞轮和剥离轮的交叠量Δ来控制送纸效果,当交叠量Δ变化时,重叠分离机构形成的有效变形宽度b也随着变化,会影响纸币通过分离机构的时间,结果如图5所示。
当只有单张纸通过时,交叠量越大,纸币受到的最大变形力越大,最大变形力分别为0.43 N,0.66 N,0.92 N,1.20N和1.51 N;纸币初始阶段由于剥离轮作用,加速度会先减小而后增大并趋于稳定至0,交叠量越大,加速度变化越剧烈,初始阶段速度减小越快,通过分离机构时趋于1.72 m/s;由于机构有效变形宽度变大,纸币通过分离机构的时间也变大,通过时间分别为 47.1 ms,47.5 ms,47.7 ms,48.2 ms和48.5 ms。
当两张纸币以相同的初始速度进入重叠分离机构时,由于初始阶段纸币2主要受到剥离轮的作用,对纸币1的影响不明显;随着交叠量的增大,纸币2的加速度先减小后增大,速度单调递减;交叠量越大,纸币2速度减小得越快,当纸币1完全通过分离机构时,纸币2的位移也最小,有利于两张纸币的分离。
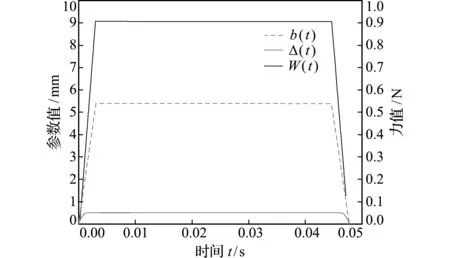
图4W(t),b(t)和Δ(t)随纸币进入重叠机构时间t的变化
Fig.4 Change ofW(t),b(t) and Δ(t) as the paper passing through the overlap separation mechanism
5.2 剥离轮转矩T对进纸阶段动态特性的影响(单/双张)
剥离轮的转矩变化如图6所示。可以看出,当单张纸币通过时,随着剥离轮转矩的增大,纸币通过分离机构的速度会降低,通过时间会略有增大。
当双张纸币通过分离机构时,对纸币2的影响较大,随着剥离轮转矩的增大,纸币2的加速度先减小后增大,速度单调递减。剥离轮转矩越大,纸币2速度减小越快,纸币1完全通过分离机构时纸币2的位移也最小,位移分别为58.9 mm,58.3 mm,57.7 mm,57.1 mm和56.5 mm。有利于两张纸币的分离,但是变化不明显。
5.3 剥离轮摩擦系数μg s对进纸阶段动态特性的影响(单/双张)
剥离轮的摩擦系数也是决定分纸效果的主要参数,剥离轮对纸币的摩擦系数要大于纸币之间的摩擦系数才能达到纸币分离的效果。
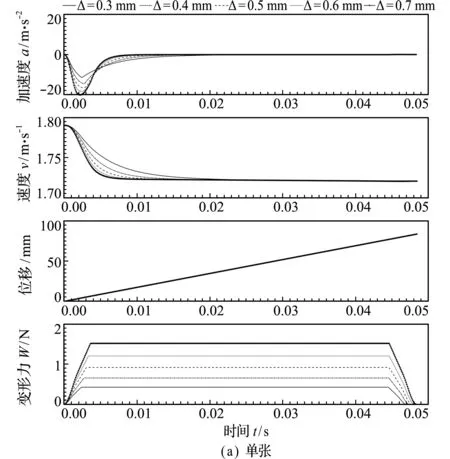
图5 交叠量Δ对单双张进纸的影响
Fig.5 Effect of overlap amount on single -sheet and double -sheet paper feeding
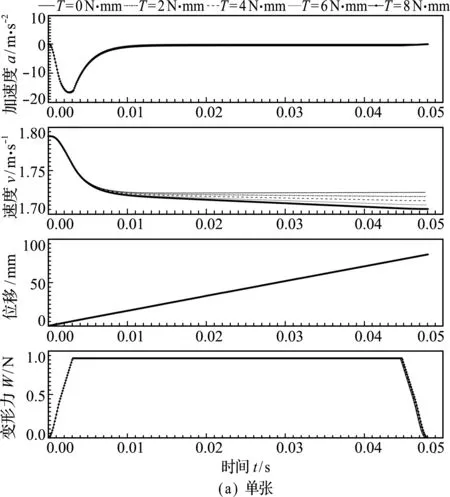
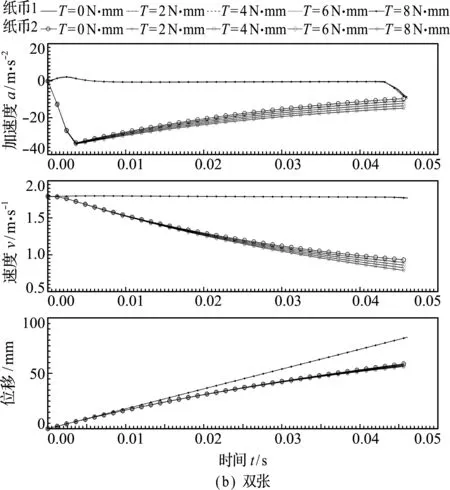
图6 剥离轮转矩T对单双张进纸的影响
Fig.6 Effect of torque of separating wheel on single -sheet and double -sheet paper feeding
剥离轮摩擦系数μg s变化结果如图7所示。可以看出,当单张纸币通过时,随着剥离轮摩擦系数的增大,纸币通过分离机构的速度降低,速度分别降为 1.74 m/s,1.72 m/s,1.70 m/s,1.68 m/s和1.67 m/s;通过时间会增大,分别为 47.4 ms,47.9 ms,48.4 ms,48.8 ms和49.3 ms。
当两张纸币通过分离机构时,纸币1通过的时间分别为46.08 ms,46.14 ms,46.2 ms,46.26 ms和46.32 ms,略微增加;纸币2所受影响较大,随着剥离轮摩擦系数的增大,纸币2速度下降较多,分别降为1.04 m/s,0.88 m/s,0.75 m/s,0.63 m/s 和0.54 m/s;纸币2位移变小,分别为63.2 mm,58.3 mm,53.9 mm,50.1 mm和 46.7 mm。
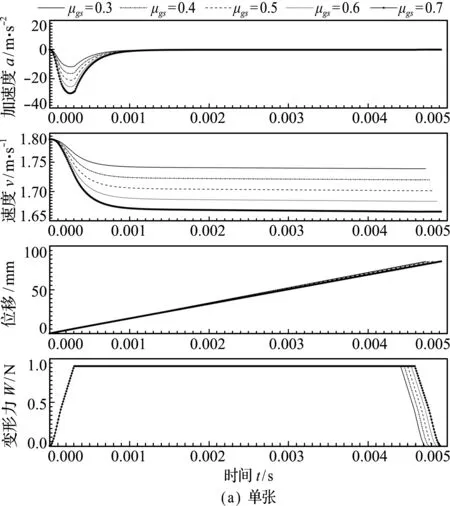
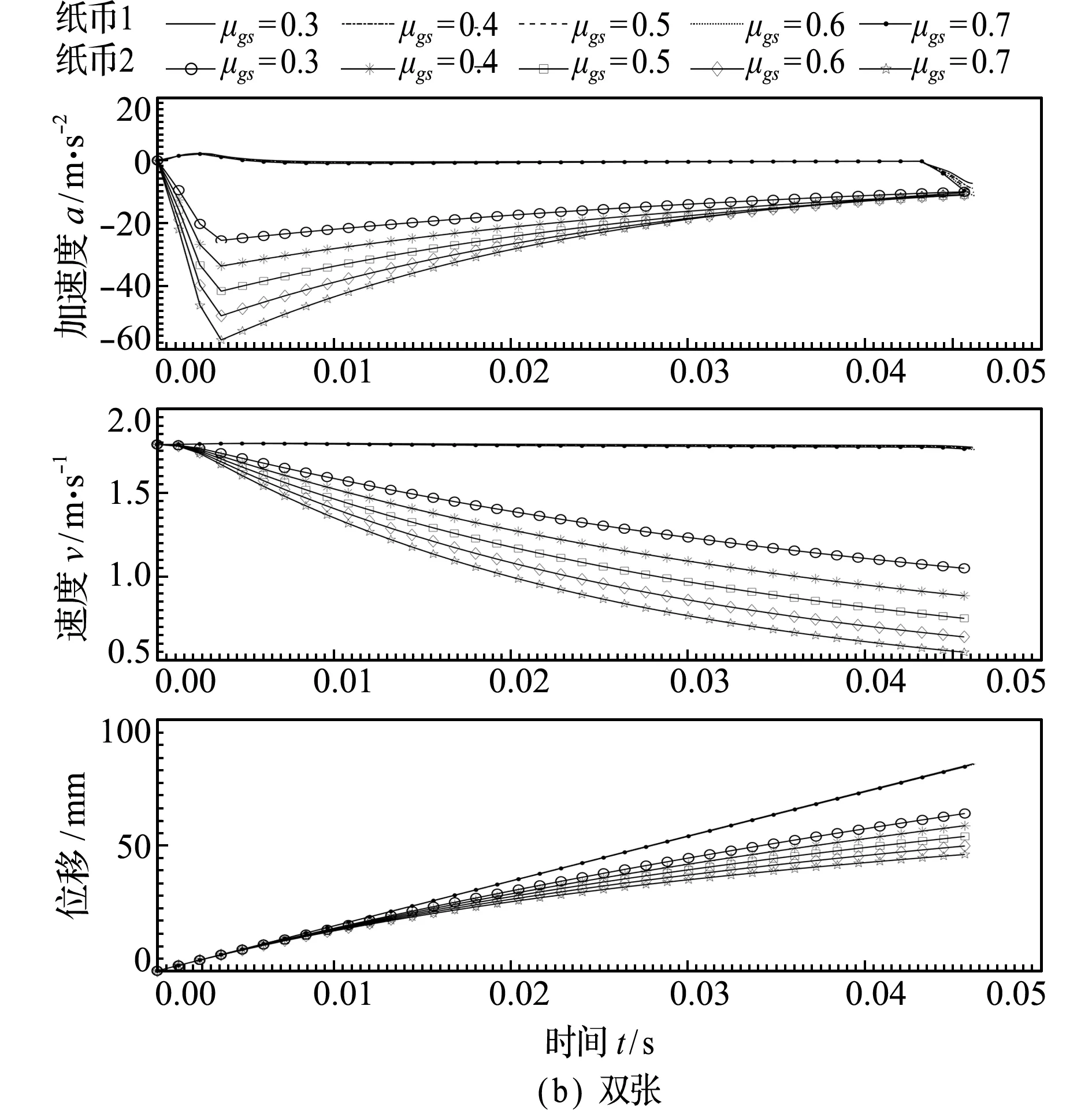
图7 剥离轮摩擦系数μg s对单双张进纸的影响
Fig.7 Effect of friction coefficient of separating wheel on single -sheet and double -sheet paper feeding
6 结 论
在建立纸币通过重叠分离机构的动力学模型中采用了修正的库伦摩擦力模型,并考虑了进纸过程中变形力的变化,通过分析重叠分离机构交叠量、剥离轮转矩和剥离轮摩擦系数对单双张纸币通过的影响,得到如下结论。
(1) 重叠分离机构的交叠量越大,单张通过时初始阶段加速度和速度变化越剧烈,通过分离机构的时间增加;双张通过时,较大的交叠量会迅速降低纸币2(连张纸币)的速度,减小其通过位移,有利于纸币分离。
(2) 剥离轮转矩越大,单张纸币通过时的速度略有降低,时间也会略长;当双张通过时,纸币2的速度和位移均略有降低,对纸币分离有利,但是影响不显著。
(3) 剥离轮摩擦系数越大,单张纸币通过时的速度降低越大,通过分离机构的时间也会增加;双张通过时,纸币2速度降低且位移也降低,可以提高纸币分离的效果。
