大数据时代下幂律分布在医学领域中的应用价值

王晓楠，刘 蕾，张 佳，王健生(西安交通大学医学部，陕西 西安 7006；陕西中医药大学第二附属医院，陕西 咸阳 7000；西安交通大学第一附属医院，陕西 西安 7006)

自Gauss提出统计概率模型以来，正态分布一直被认为是一种基本的概率模型[1]，其概率密度函数可表示为：

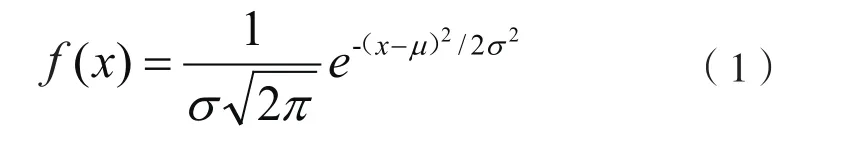
身高、学校成绩、天气预报和人类生活的其他不同方面都被认为遵循正态分布。因此，该模型被用于医学、人文科学、社会科学以及测量等多学科领域中。然而，并不是所有的自然现象都发生在平均水平或其附近，例如，社会财富的分布和城市地区的规模往往表现出极端的两极分化，规模较小的事件发生的概率很大，而规模较大的事件很少发生，这样的特征很难用一般的值或均值来表征，而幂律分布对于发生频率较低的事件仍能用“长尾”累计分布曲线来表示。此外，其他的大小事件也可以用幂律分布来描述，从而解释自组织的临界状态或复杂性的存在[2]。随着大数据时代及全球化和社交媒体等因素造成了更多的相互关联和复杂性，幂律行为已成为一种趋势。在医学领域中也陆续发现在神经元构成的小世界网络及食管pH值的频率分布、脉络膜毛细血管层的流量大小等方面均存在幂律现象，因而在医学领域中应用幂律分布具有深远的意义。国外对幂律分布在医学领域中的应用已开始研究并应用，而国内却极少。该文对幂律分布的概念、相关模型、形成机制以及幂律分布的普适性进行综述，从而思考幂律分布在我国医学领域中的应用，以期为幂律分布在医疗护理领域中更深入、更广泛的应用提供借鉴和参考。

1 幂律分布的概念、相关模型以及形成机制

1.1 幂律分布的概念

幂律分布[3]是由意大利经济学家Vilfredo Pareto于1896年关于社会财富收入分配不均的研究中第一次定量发现。它是一个概率分布函数，用数学公式定义为：

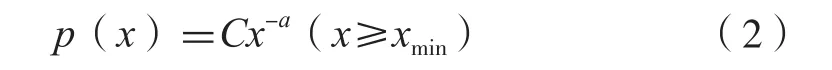
其中，x为正的随机变量，p(x)为对应的概率，a为幂律指数，c为常数，xmin为x满足幂律的最小值。幂律分布最经典的模型如图1所示，其长长的尾巴由Chris Anderson命名为“长尾”。Kumamoto等[4]指出幂律是惟一满足无标度性质的函数，对公式(2)两边取对数，得：

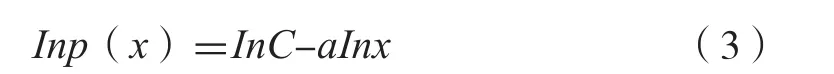
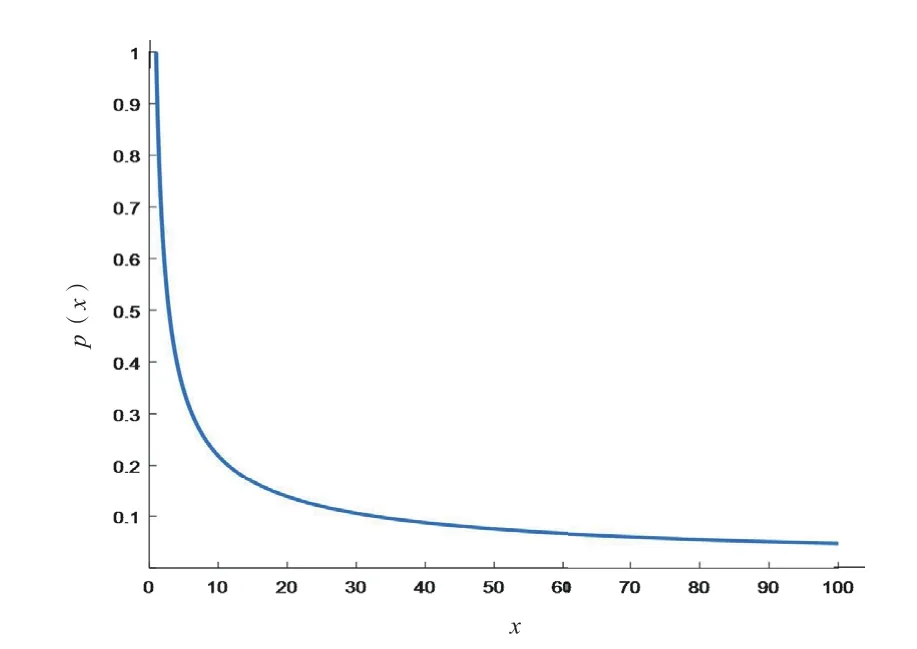
图1 幂律分布经典模型

与满足线性关系。在双对数直角坐标系下，幂律分布表现为斜率为幂指数负数的一条直线，这一线性关系是判断实例中给定的随机变量是否满足幂律的依据。

1.2 幂律分布常见模型

1.2.1 Pareto定律 Pareto定律由Vilfredo Pareto发现，并且提出了著名的80/20原则，即20%的人口占据了80%的社会财富。用公式可表示为：

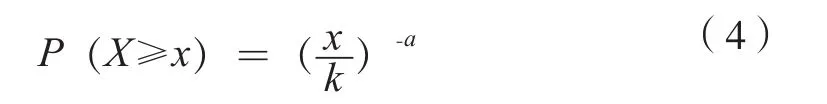
对公式(4)求导转化而得Pareto分布的密度函数，即：

式(4)、(5)中，a为Pareto指数，且a＞0，k为尺度参数，k＞0，x为随机变量，x≥k，P（X≥x）是大于等于x的概率。

1.2.2 Zipf定律 Zipf定律是1932年哈佛大学的语言学专家Zipf发现，用公式表示为：

其中，r表示一个单词出现频率在语料库中的排名，P(r)表示排名为r的单词的出现频率，a为幂指数，且为常数。r与P(r)之间为反比关系。该定律表明人们在动态过程中总能找到能量消耗最少的途径，即符合“最小努力原则”。

1.2.3 Gutenberg-Richter定律[5]Charles Francis Richter和Beno Gutenberg于1956发表的一篇论文中首次提出的地震震级和频率之间的关系，用公式表示为：

或可对公式(7)进行对数转化得：

式(7)和式(8)中：N为震级≥M发生的次数，a，b均为常数。

1.3 幂律分布的形成机制

1.3.1 增长与优先连接 增长以及优先连接的含义即为其字面意思，符合“马太效应”[4]。Barabási与Albert[6]针对复杂网络中普遍存在的幂律分布现象，提出了网络动态演化的B-A模型。他们认为增长和优先连接性是无标度网络度分布呈现幂律的两个最根本的原因。

1.3.2 基于几何布朗运动的随机模型 许多表现出幂律行为现象的时间演化通常被认为是涉及一个变化的，但大小独立的比例增长率，从数学上可以用几何布朗运动(Geometric Brownian Motion，GBM)来建模，即：

其中，X为随机变量，μdt为系统成分，σdw为随机成分。GBM可以看作是简单指数增长的随机版本。

1.3.3 自组织临界理论 自组织临界理论一直被认为是产生幂律分布的动力学原因。它认为，由大量相互作用的成分组成的系统会自然地向自组织临界态发展，当系统达到这种状态时，即使是很小的干扰也可能引起系统一系列灾变。其中，Bak等的“沙堆模型”便形象地解释了自组织临界理论的形成，“临界”是指流沙崩落能发生在任何长度的标尺上，“自组织”表示系统自己将自己调到了临界状态[7]。

1.3.4 HOT理论 HOT理论[8]是由加州大学圣巴巴拉分校的Jean Carlson以及加州理工学院的John Doyle提出，即当一个系统处于稳定状态时，外部因素的一个小小的干扰都能引起系统巨大的变化。当一个系统处于HOT状态时，该系统满足幂律分布。

2 幂律分布的普适性及其在医学领域中应用

2.1 幂律分布在自然、社会等学科中的应用

幂律分布广泛存在于自然、社会等多个学科之中，且其表现形式多种多样。包括进出口波动对产业产出的影响[9]、学术期刊影响力的分布[10]、供应链网络中结点连接度的概率分布、社交网络上用户行为数据的分布[11]、复杂网络等都是服从幂律分布的典型现象。且有更多的领域也在尝试利用幂律分布的方法对该领域进行更加深入的研究。在对电动汽车的研究中，王岱等[12]利用人类个体的移动距离良好地符合截断幂律分布，从而推测车辆的移动也符合类似的定律，并采用柯尔莫格洛夫—斯米尔诺夫(Kolmogorov-Smirnov，KS)拟合优度检验来验证，结果表明幂律分布可良好地表示实际数据分布情况。在风电场出力场景中，利用风速廓线模型即大气边界层内风速大小随高度变化的切边定律计算风机轮毂高度处的风速[13]。幂律衰减可定量地衡量意见领袖在微博消息传播中所表现出的影响力[14]。在复杂电力系统中也可能存在着幂律分布[15]。

2.2 幂律分布在医学领域中应用现状

2.2.1 基础医学 在基础医学中，细胞几乎贯穿于基础医学的各方面。且活细胞的数千个成分是动态相互连接的，细胞的功能特性最终被编码成复杂的细胞内分子相互作用网络。鉴于幂律分布在互联网中的发现与应用，Wagner等[16]对大肠杆菌代谢网络进行了图论分析，发现该网络是一种有别于规则网络和随机网络的图形，其遵循幂律分布。随后，有学者更是将网络细分化，其团队将43个不同生物体，包括细菌(大肠杆菌)、真核生物(酿酒酵母)等组成的代谢网络被组织成许多小的、高度连接的拓扑模块，它们以分层的方式组合成更大、更不凝聚的单元，其数目和聚类程度遵循幂指数为2.2的幂律分布[17]。随着时代的发展，幂律分布在医学领域被逐步地发现，在神经元领域中，Klaus等[18]利用KS统计量和极大似然方法将神经元雪崩的幂律模型与指数分布和基于KS距离的各种重尾分布进行了比较，发现幂律分布与指数、对数正态分布和伽马分布相比较更适合神经元雪崩中的团簇大小分布，其斜率接近于-1.5。其后，2012年Samura等[19]利用CA3切片培养模型再现了CA3切片培养中同步的幂律尺度。在模型中，每个神经元都与其他神经元连接，形成小世界网络。结果表明，当突触权重为对数正态分布和抑制平衡时，切片模型中的幂律标度具有高鲁棒性，即幂律尺度在小世界网络中得到了有力的再现。Karmeshu等[20]于2014年基于超统计的框架提出当多个神经元聚集在一起并一起发射时，会产生穗间隔分布中的幂律行为，且在亚阈值区内，大量神经元上的膜电位也出现幂律行为。

2.2.2 临床医学 幂律分布在基础医学被发现后，临床医学的研究也开始逐渐发现幂律分布。例如，Decena等[21]证明胎儿心率变异性在功率谱中表现为逆幂律关系。Gardner等[22]对57例胃食管反流性疾病患者和26例正常人进行食管pH值测定以观察两者不同食管pH值的频率的研究结果，发现在两组之间，食管pH值的频率均是具有幂律分布特征的。近年来，幂律分布在临床医学中被发现的频率也一直在增加。其中，在研究脑活动领域中，Jonathan等[23]将脑活动的多位点局域场电位(local field potential，LFP)记录进行了分析，结果表明，被定义为负LFP峰的事件大小分布可以接近幂律分布。从离体切片电生理学到人体功能性磁共振成像，各种体外和体内记录都有神经系统活动动力学的迹象。然而，对于大脑究竟是在临界状态下运作，还是在另一种控制状态下(如随机或振荡动力学)，并没有一致性的意见，而对神经系统数据的临界性检验的工具之一便是幂律分布，Tinker等[24]在2014年应用幂律分布来检验自闭症儿童和非自闭症儿童在执行功能任务时，脑磁图记录所得的相位同步的分布是否存在幂律行为的研究发现，相同步指数分布中的幂律标度在对照组和孤独症组中并不常见，其发生频率也是相似的。此外，幂律尺度往往随着认知负荷的增加而减小(难度或参与任务)。2016年，Spaide[25]在使用光学相干断层扫描血管造影术调查脉络膜毛细血管层的流量特性时，对收集到的80例患者数据进行分析时，发现流动空隙的分布与大小也遵循幂律分布。在用于治疗肿瘤放疗用的正电子发射断层扫描(positron emission tomography，PET)也发现利用幂律函数，可以计算滤波函数，从而可以确定PET信号的远端落区，确定质子束的射程[26]。

2.2.3 其他 在关于医学的其他方面，幂律分布也有被发现，例如医学网络的数据分布频率、基因之间、蛋白质之间的距离分布等。在基因方面，2014年，Polychronopoulos等[27]通过研究连续保守非编码元素(conserved noncoding elements，CNE)之间的距离的统计特性来研究CNE的染色体分布时，发现CNE的距离为幂律分布。另有学者发现CGIs的基因组以及人类基因组中Alu和LINE 1元素的空间排列中以及距离上满足幂律分布[28-29]。在2016年，Gouda等[30]分析了人类单核苷酸多态性(single-nucleotide polymorphisms，SNP)在全基因组范围内的分布，研究结果表示SNP之间的距离分布也近似幂律分布。可见，大多数基因在空间距离上满足幂律分布。随着大数据以及数字健康社会网络(digital health social networks，DHSN)的兴起成为医学领域的研究热点，2015年，有学者指出，幂律分布是解决大数据最常用的统计学分析方法，且幂律可看作是从社会媒体、网络活动和人口普查数据等来源收集的人类产生的大数据的基本模型[31]。Van Mierlo等[32]对DHSN的数据分布频率进行研究后发现尽管在主题、内容和存在时间上存在着巨大的差异，但DHSN遵循幂律的性质。

3 幂律分布在我国医学领域中应用的不足

幂律分布现象广泛存在于众多领域，包括医学领域，但其之所以在医学领域开展缓慢，可能与幂律分布被关注的时间相对于正态分布等其他统计学方法较晚，而且更多属于统计物理、数学范畴领域，且幂律分布种类繁多，产生机制复杂，其模型就有上千种，深入理解较为困难。此外，随机过程可以在不存在潜在的自组织临界性的情况下产生伪幂律缩放[27]。因此，在应用幂函数对数据进行处理时选择性会较大，困难性也较大。

我国大多应用幂律分布的领域为计算机、物理、金融学等，而在医学领域中应用幂律来分析数据的研究较少，而国外已经有学者从基础医学、临床医学以及医学网络等方面着手采用幂函数分析数据，得出幂律分布，解释未能解释的现象，为医学现象提供更加合理化的解释。我国也应借鉴国外经验，在对数据进行分析时，可考虑采用合适的幂函数的方式，以更好地发现幂律分布，从而解释医学界中存在的一些现象。

4 结语与展望

幂律分布自19世纪发现以来，已为多学科中的现象提供了可解释的依据，该统计方法并不是目前医学学者所习惯采用的分析数据的方法，但其对数据的要求度低，能够很大程度地利用数据，且对于不经常发生的事件，用幂律解释的风险比用正态分布解释的风险分析更为重要，在对不能使用正态分布的事件中发挥着重要的作用。

近年来，应用其研究的领域一直在逐步扩大，医学卫生领域作为一个大模块，也越来越受到关注，其弥补了正态分布所不能解释的数据规律，大大提高了对数据的多重分析。且由于全球化和社交媒体等因素，幂律也会越来越被重视，在医学领域中逐步发现幂律分布也会成为一种趋势。未来中国可先从基础医学方面发现此规律，以此为基础推动其在医学领域的应用，丰富统计学方法以及医学规律的发现。