基于离散-连续耦合方法的隧道压力拱特性研究
2020-05-22谭绪凯陈晓宇丁其乐
高 峰,谭绪凯*,陈晓宇,丁其乐,李 星
(1.重庆交通大学 土木工程学院,重庆 400074; 2.中机中联工程有限公司,重庆 400039;3.林同棪国际工程咨询(中国)有限公司,重庆 401121)
1 引 言
隧道压力拱理论是隧道深浅埋界限划分的基础,对隧道工程计算及设计具有重要作用。自Kovari[1]首次提出隧道开挖过程中的成拱效应以来,相关学者就隧道压力拱问题展开了大量的研究。在压力拱的定义上,目前普遍认为隧道压力拱的形成为力的传递路径的改变所致,认为压力拱是指洞室开挖后的卸荷效应破坏了初始应力场的平衡,导致围岩不均匀变形和应力重分布,围岩体系的荷载传递路线发生偏移,主应力大小和方向随着荷载释放逐渐发生改变,最终在洞室周边形成类似拱形的围岩保护圈[2-6]。
目前,针对隧道压力拱问题的研究主要集中在压力拱成拱机理、压力拱演化规律及压力拱范围等方面[7-9],其研究手段主要为模型试验方法和数值模拟方法,而模型试验手段易受研究成本、边界效应、模型尺寸、试验周期及人为因素等影响,数值模拟手段成为最为普遍的研究方法。目前,常用的数值方法主要分为连续介质数值方法[10-12](如有限元法和有限差分法等)和非连续介质数值方法(如离散元法等)。从研究成果发现,连续介质方法无法从微观角度直观分析和观察隧道压力拱的形成机理及发展特性。
随着离散元理论的发展,其广泛应用于岩土工程的微观力学行为研究,在压力拱研究方面也有初步尝试。如扈世民等[13]采用颗粒流程序PFC2D研究了大断面黄土隧道的塌落拱和压力拱的发展过程,直观得出了黄土隧道破坏演化过程,并从应力场角度推出了压力拱的外边界。但是地下工程为半无限体,进行研究时需要选取较大的模型降低人工边界对计算结果的影响,此时采用离散元程序计算时需要成千上万的颗粒,需要大量的计算机存储空间和计算时间,对于计算机水平要求太高。
耦合算法自20世纪80年代初期由Felippa等[14]提出以来,得到了长足的发展。有限元法能很好地反应连续介质力学性能,且对计算机存储空间和计算时间要求较低;离散元法能很好地模拟非连续介质力学性能。因此,连续-离散耦合模型能充分发挥两种方法的优势,且能直观反映隧道开挖后的围岩受力发展机理。目前,其已成为国内外研究的一个重点方向。严琼等[15]分别采用FLAC和PFC建立了连续模型和离散模型,从连续-离散模型的数据一致性实现耦合,研究了边坡工程的稳定性;徐国文等[16]基于离散元-有限差分耦合算法,研究了层状软岩隧道开挖后的围岩破坏机理;金炜枫等[17]基于改进后的离散-连续耦合模型对地下结构地震过程中的破坏过程进行了模拟。目前,隧道及地下工程的离散-连续耦合模型研究已经取得了一些进展,但其准确性及适用性依然值得进一步研究。
离散-连续耦合的关键在于交界处的模拟方法及模拟效果。周健等[18,19]通过保证外围连续单元和内部离散颗粒在耦合过渡区的力或速度的一致,实现了离散-连续模型的耦合。张锐等[20]通过编程,基于离散-连续模型耦合过渡区的动量传递的连续性及空间-时间的双耦合,实现了离散-连续模型的耦合。张铎等[21]从两个方面实现了离散-连续模型的耦合,一方面通过速度实现连续单元向离散颗粒的过渡(耦合过渡区连续单元的节点速度通过形函数分配到离散颗粒),另一方面通过力的传递实现离散颗粒向连续单元的过渡(耦合过渡区离散颗粒的平均应力施加在连续单元上)。
本文采用二维颗粒流程序PFC2D,基于离散-连续耦合方法对隧道施工的压力拱进行了研究。在距离隧道洞室较远区域,通过连续模型模拟总体的受力及位移;在洞室周边围岩,采用离散元模型研究了隧道施工过程中周边围岩力的传递路径的变化,进而直观展现了隧道开挖后压力拱的成拱过程及成拱范围。
2 离散-连续耦合计算方法确定
2.1 离散-连续耦合程序的实现思路
基于现有离散-连续耦合思路,本文提出以下优化思路。离散-连续耦合模型的关键是离散元模型与连续介质模型之间的边界处理和过渡方式,离散颗粒和有限单元之间存在接触,两者间的接触力可通过接触点的位移进行计算。该接触力可通过荷载形式施加在离散颗粒上,也可以外荷载形式施加在有限单元上,进而实现交界面上相互作用的连续性。考虑到有限单元的受力特点,本文对于施加在有限单元上的荷载进行一定处理,取一定范围离散颗粒的平均应力。基于上述耦合思路,通过力的传递,编写连续单元算法和耦合算法嵌入到PFC2D程序中,实现耦合计算。
2.2 平均应力计算方法
在离散-连续模型交界面上,一侧是有限单元,一侧是离散单元,如图1所示。
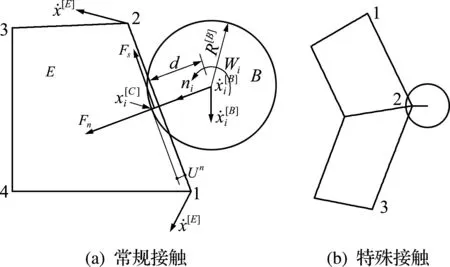
图1 颗粒与单元接触示意图
Fig.1 Contact geometry between ball and continuum element
目前,颗粒与连续单元间的力及重叠厚度求解方法已有成熟的研究成果。颗粒与连续单元是否接触通过颗粒圆心到临近单元边界距离与颗粒半径之间的大小来确定。图1(b)为颗粒与连续单元之间接触的一种特例,颗粒接触到两个单元的交点处,该情况通过颗粒圆心与交点间的距离进行接触与否的判定,接触力的方向为结点2到颗粒圆心的方向。为了避免此种情况计算多次接触力,规定此种情况下,颗粒只与边界的起点相接触,而与边界的终点不算接触,即图1只与2-3段接触,与1-2段不算接触。接触力只要2-3段与颗粒计算,方向为结点2指向颗粒圆心。
考虑到连续单元的应力是单元面积内内力的均值,因此,接触单元的应力应是耦合过渡区域一定范围内离散颗粒的接触力的平均值。一个体积为V的区域的平均应力可由式(1)求得[22],
(1)
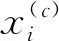
一定区域的孔隙比为
n=1-Aball/Aregion
(2)

(3)
2.3 平均应力计算区域面积的确定
耦合过渡区域的合理区域的选定对力的传递准确性至关重要。本文对比了如下3种方案。
(1) 按照过渡区域连续模型单元大小确定区域面积,遍历该面积内的颗粒,计算其平均应力,孔隙率近似采用初始孔隙率。该方案不能保证该区域内颗粒与单元的质量相等。
(2) 在接触单元的相邻位置放置测量圆,其直径按照该单元的最大边长取值,由测量圆获取该区域的平均应力。该方案可保证孔隙率的准确性。
(3) 方案3近似于方案2,但其主要通过测量圆获取该区域的平均应变,进而通过本构方程得出平均应力。
为了选取最佳区域确定方法,对上述3种方案与全连续模型进行对比计算。平面模型计算范围取10 m×10 m,在模型正中间区域的2 m×2 m范围建立离散元模型,如图2所示。
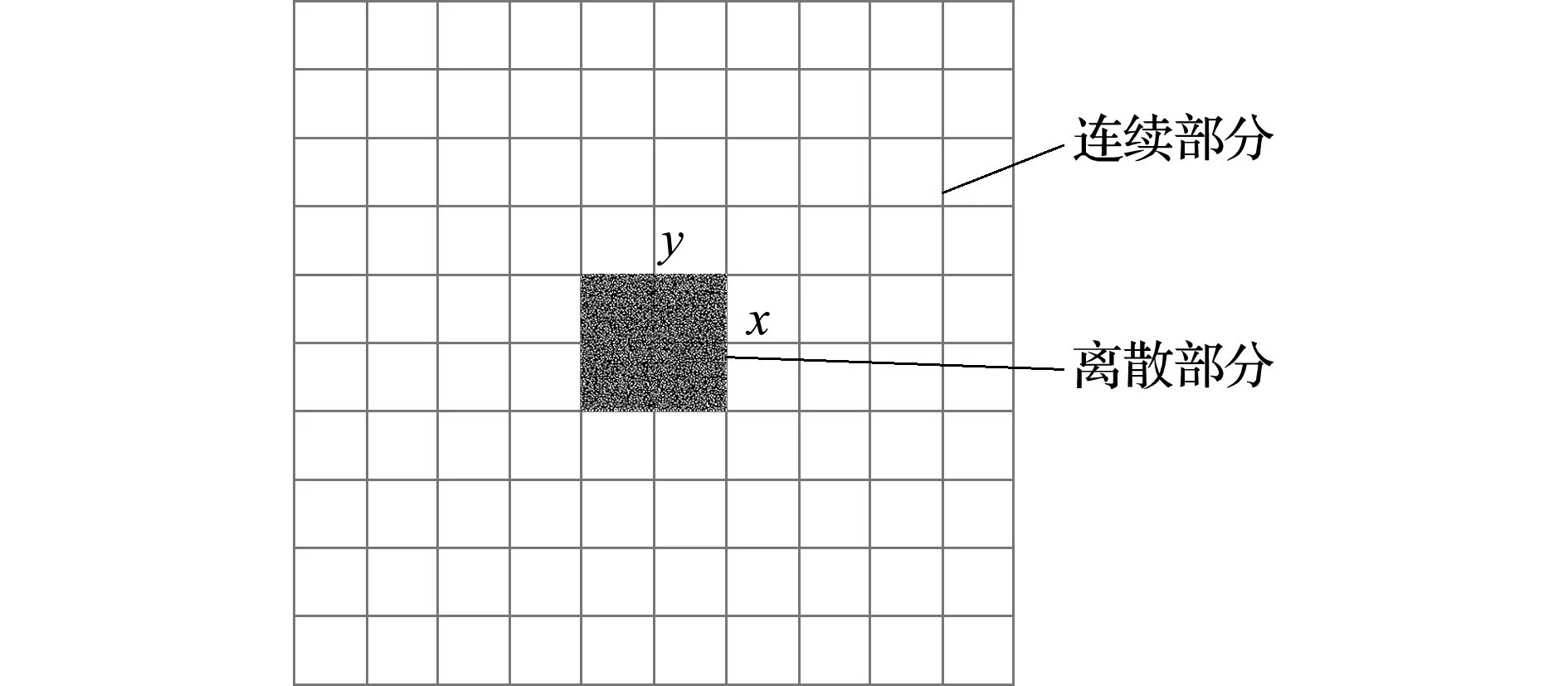
图2 耦合计算模型
Fig.2 Model of coupling calculation
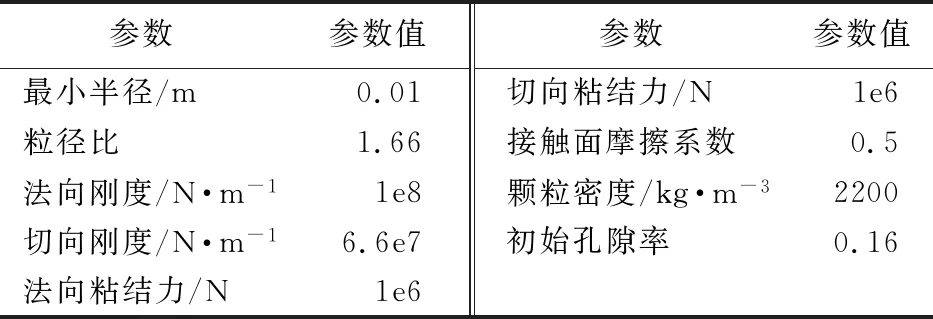
计算采用contact-bond模型,目前微观参数主要通过试凑方法获得,由于本文主要验证程序的有效性,所以参数设定思路是给定确定的微观参数,然后利用FISHTank的模拟室内压缩试验的程序计算弹性模量和泊松比。给定的微观计算参数列入表1。
表1 耦合模型微观参数
Tab.1 Microcosmic parameter of coupling calculation
参数参数值参数参数值最小半径/m0.01切向粘结力/N1e6粒径比1.66接触面摩擦系数0.5法向刚度/N·m-11e8颗粒密度/kg·m-32200切向刚度/N·m-16.6e7初始孔隙率0.16法向粘结力/N1e6
由FISHTank程序模拟无侧限单轴压缩试验,得到模拟压缩曲线,如图3所示。可以看出,颗粒模型的宏观参数为弹性模量Es=44 MPa,泊松比υ=0.14,平均密度ρ=1848 kg/m3。
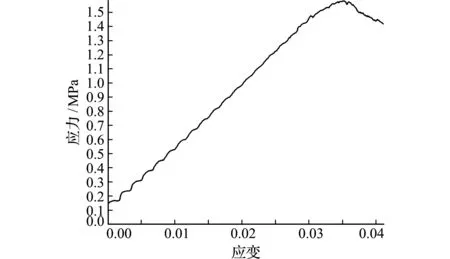
图3 应力-应变曲线
Fig.3 Stress -strain curve
模型计算荷载选取自重荷载,得到重力作用下体系的应力场和位移场,并与FLAC计算结果进行对比。各方案计算结果相对于FLAC计算结果的相对误差列入表2。
表2 3种方案相对误差最大值对比
Tab.2 Maximum relative error comparison of three kinds of solution
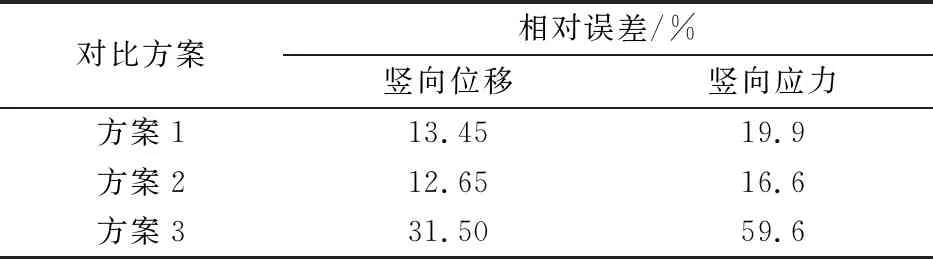
对比方案相对误差/%竖向位移竖向应力方案113.4519.9方案212.6516.6方案331.5059.6
由表2可知,方案3误差最大,这是由于在计算应力时,颗粒间隙的应力为0,而在颗粒间隙间的速度不为0。利用测量圆的平均应变计算得到的应力值较小,与对应的连续单元的应力相差很大,导致误差较大。方案1和方案2的误差几乎相当,方案2的误差略小。故最终通过方案2确定平均应力计算区域的面积。
由表2可知,耦合软件计算结果与FLAC2D程序计算结果存在一定的误差,将两者沉降量和应力值的相对误差整理得出误差等值线,如图4所示。可以看出,耦合程序的沉降结果普遍大于FLAC2D程序计算结果。其中,空单元附近误差值最大,远离空单元的位置误差相对较小。由于保证了总体围岩的受力特性,并且通过调整内部离散元颗粒的微观参数保证内部离散颗粒计算精度,因此,耦合程序的交界面处的误差对后续研究影响较小。
2.4 耦合程序遍历颗粒方法的确定
在计算连续单元的交界面上接触力时,耦合程序需要遍历所有的颗粒,确定与连续单元存在接触的颗粒,通过其接触点的力求解边界平均应力。程序如果每次都需遍历所有的离散颗粒,将耗费大量的计算时间。本文考虑到隧道开挖过程中,远离隧道开挖区域的围岩稳定性较好,其内部颗粒一般不会窜跑到离散-连续模型的交界面。因此,提出遍历的离散颗粒只包含模型交界面向内的三层颗粒,如图5所示。
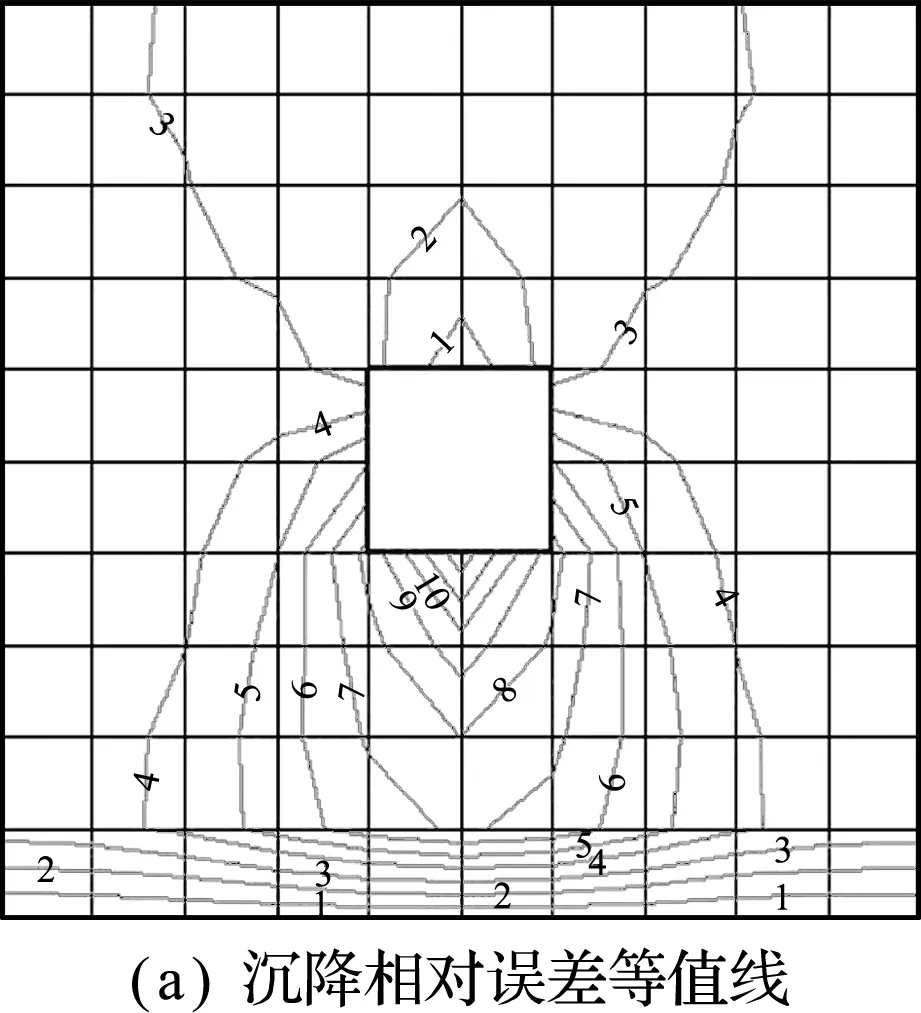

图4 相对误差等值线
Fig.4 Contour map of relative error
3 程序执行过程
离散-连续耦合模型计算流程如图6所示,计算流程中的主要程序函数如下。
(1) FP_startup函数。 通过该函数程序实现连续单元程序拟FLAC2D和离散元程序PFC2D的初始化设置。
(2) FP_flacstatic函数。 在离散元程序PFC2D计算完成后运行该函数,提取PFC2D中颗粒接触应力,并将应力结果作为边界条件施加到连续单元上,通过拟FLAC2D程序进行motion计算。进而进行连续单元程序的计算。
(3) FP_flacdyn函数。 该函数与FP_flacstatic函数属于一个计算过程,主要负责拟FLAC2D中的动力计算模块。
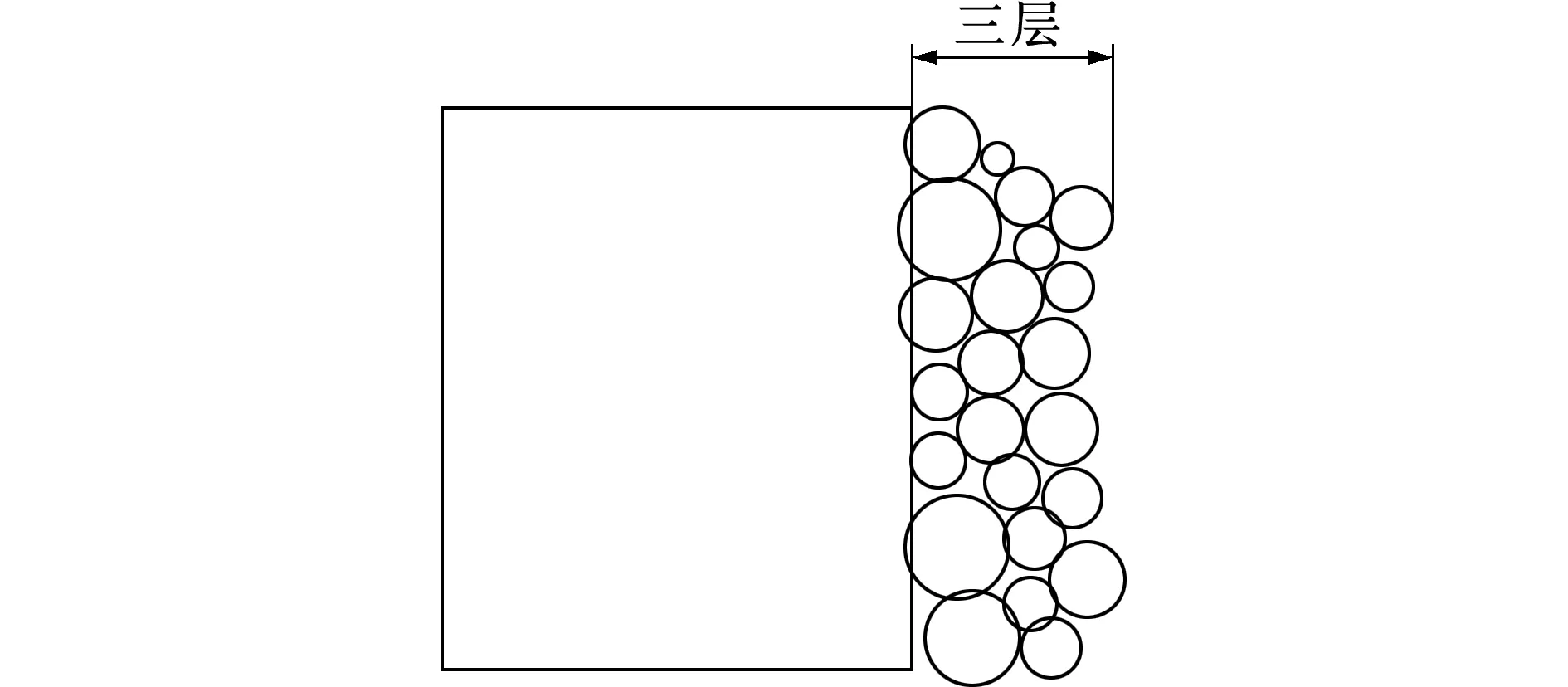
图5 耦合算法中遍历颗粒示意
Fig.5 Sketch of ball needed to ergodic in coupling algorithm
(4) FP_scanball函数。该函数主要是计算连续单元的交界面(本文称之为段)上的接触力,并将其施加到相应的颗粒上,其计算方法是通过连续单元交界面节点位移计算出相应位置的离散颗粒的等效力,将该等效力施加到相应离散颗粒上。进而进行离散单元程序的计算。
离散-连续耦合模型计算中,时间步设置对程序正常运行影响较大,主要根据以下几点进行设置。① 初步应满足同时小于FLAC和PFC的临界时间步; ② 隧道开挖模型中假定颗粒与接触面之间不承受拉力,如果时间步设置过大,会由于重力加速度的作用,单个颗粒的速度过大,导致隧道顶部颗粒与接触面出现分离,因此,需要通过试算调整合理的时间步,直到颗粒与接触面不出现分离现象为止。
4 压力拱的形成过程及原理分析
4.1 模型及参数
通过离散-连续耦合程序模拟计算了隧道开挖过程。模型范围取60 m×60 m,隧道取半径为 2 m 的圆形隧道,隧道埋深取18 m。隧道区域及隧道附近的20 m×20 m区域建立离散模型,其他区域建立连续模型。计算模型如图7所示。通过FISHTank程序模拟无侧限压缩试验得到离散颗粒的宏观压缩模量为E=4.0e8 Pa,泊松比为 0.14。其宏观密度为1848 kg/m3。离散模型计算参数列入表3。
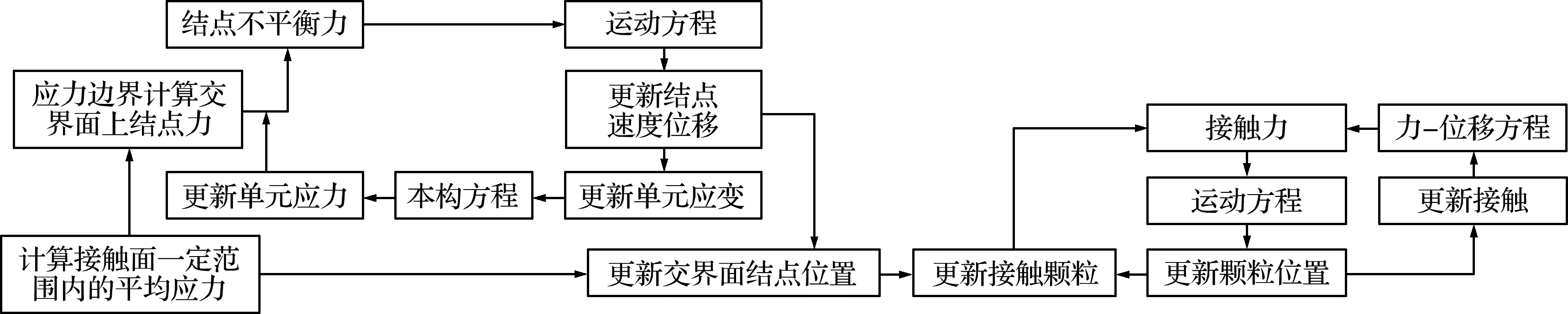
图6 离散-连续耦合计算流程
Fig.6 Flowchart of discontinuum-continuum coupling calculation
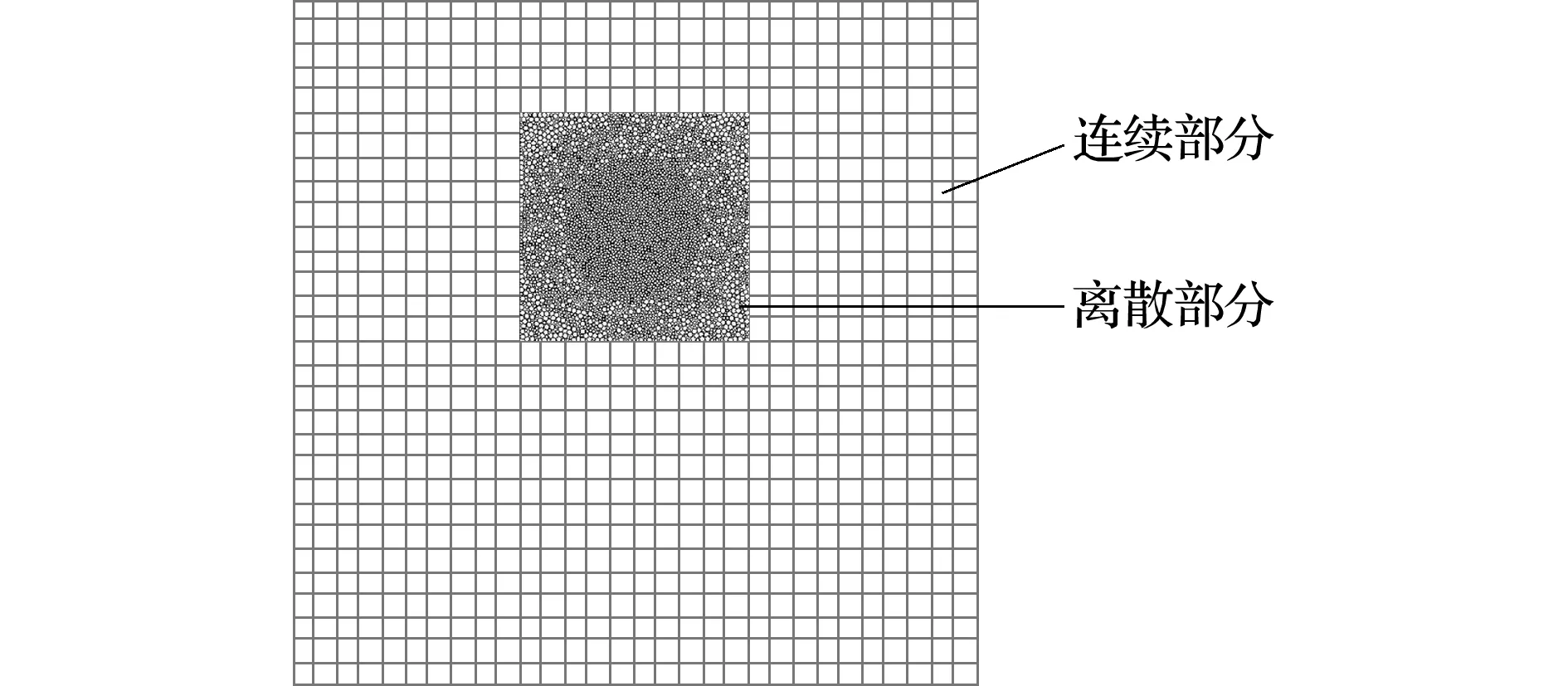
图7 数值模型
Fig.7 Numerical model
表3 离散颗粒的微观参数
Tab.3 Microcosmic parameter of discrete particle
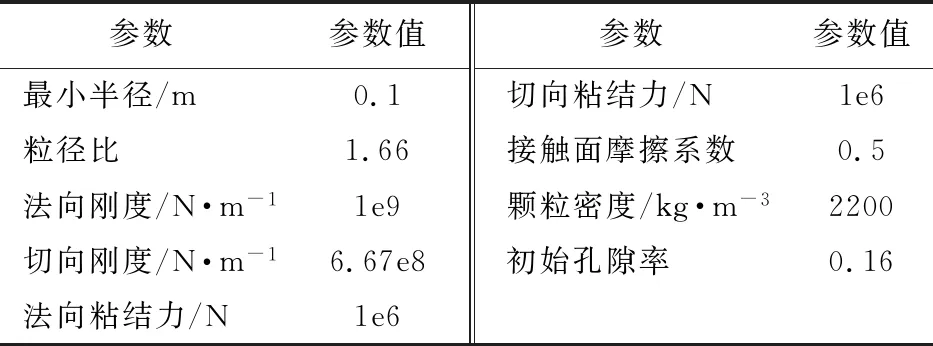
参数参数值参数参数值最小半径/m0.1切向粘结力/N1e6粒径比1.66接触面摩擦系数0.5法向刚度/N·m-11e9颗粒密度/kg·m-32200切向刚度/N·m-16.67e8初始孔隙率0.16法向粘结力/N1e6
4.2 压力拱计算结果分析
隧道体系在自重作用下,最大为竖向应力,隧道开挖后压力拱效应也主要表现在拱顶区域竖向应力的变化。因此,分析时主要调取竖向应力分析压力拱效应,如图8所示。可以看出,隧道开挖后,在拱顶和仰拱底附近应力很小。这是由于该处围岩发生塑性变形或者开裂,荷载由深部围岩承担。
图8呈现了隧道开挖后,围岩最终的应力状态,在拱顶和仰拱底形成了拱形的小应力区,体现出压力拱效应。为了更形象地呈现压力拱的形成过程,将图8中显示的应力最终状态减去开挖前的初始应力状态,绘制出隧道开挖过程中的应力变化,如图9所示。可以看出,隧道开挖后,拱顶和仰拱底附近的围岩应力急剧减小,边墙附近围岩应力升高,承载拱圈逐渐形成。
隧道施工后的压力拱形成的主要原因是围岩力的传递路径的变化。在PFC2D程序中,可通过颗粒间接触力的大小和方向的变化分析隧道开挖的压力拱效应,如图10所示。图中,深色为压力,浅色为拉力,线宽表示力的大小。可以看出,隧道开挖后,隧道周边围岩的力的传递方向发生偏转,以隧道上方围岩为例,力传递向了拱腰区域。从总体来看,隧道开挖后,拱顶区域力链很稀疏且线宽很细,表明该区域围岩对于围岩承载能力的贡献很小,拱顶区域出现压力拱现象。
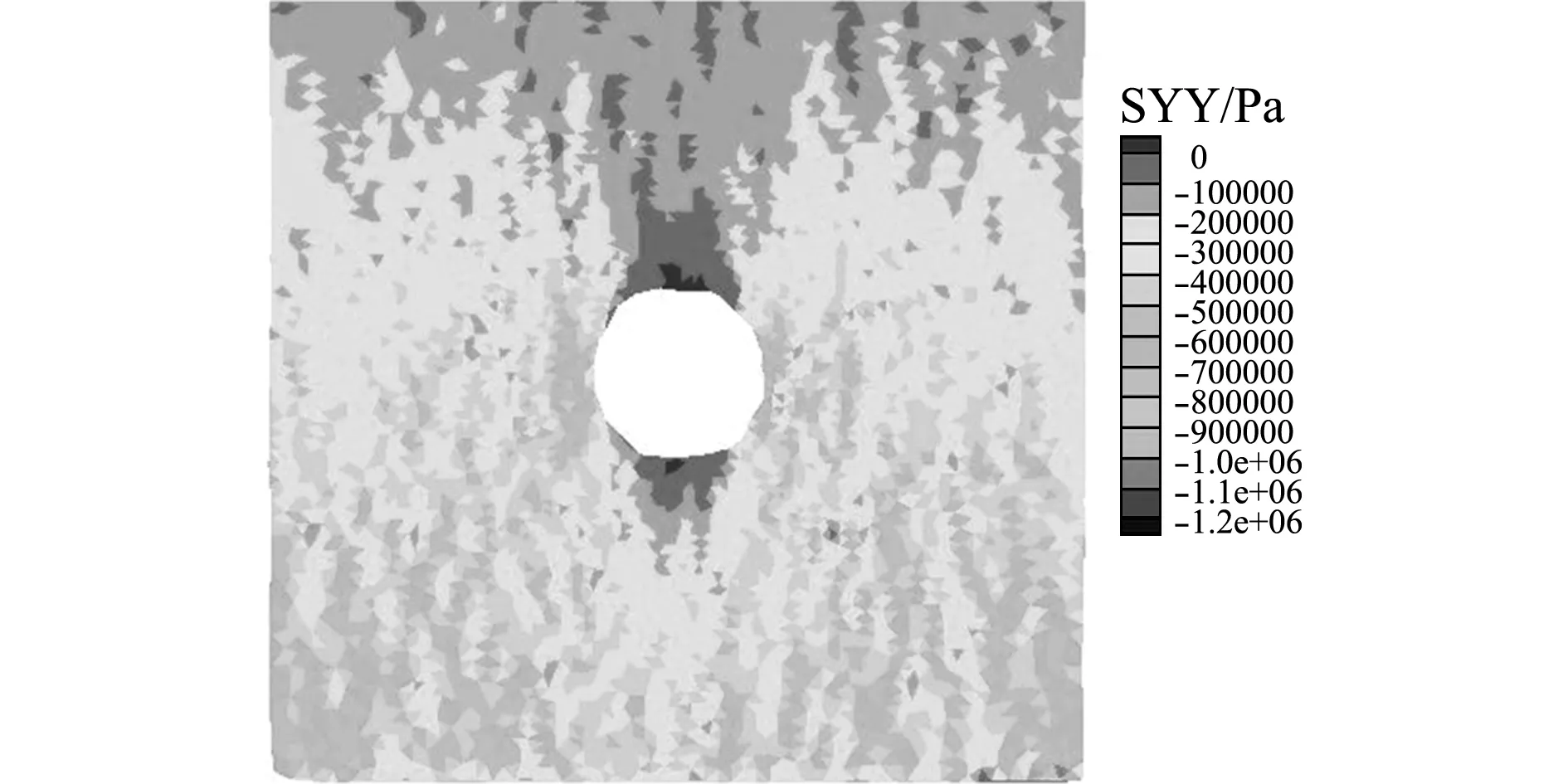
图8 竖向等效应力云图
Fig.8 Equivalent vertical stress
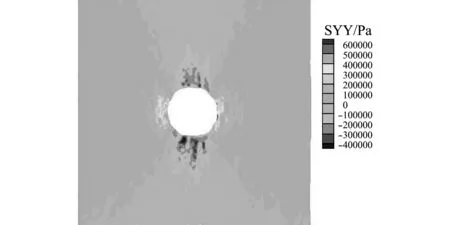
图9 竖向等效应力变化
Fig.9 Variety of equivalent vertical stress
进一步通过隧道开挖前后周边围岩离散颗粒接触力的变化呈现围岩力的变化和成拱效应,如 图11 所示。图中,红色表示颗粒的接触力降低,黑色表示颗粒的接触力升高。
可以看出,
(1) 隧道开挖后,边墙附近的围岩颗粒的接触力全部升高,且升高程度较大;拱顶和仰拱底附近的围岩颗粒的接触力既有升高也有降低,但升高程度小,降低程度大;拱顶和仰拱底颗粒升高的接触力力链在边墙处交汇。
(2) 在拱顶和仰拱底区域的围岩颗粒的接触力变化幅度沿径向逐渐减小;降低的接触力的连线基本上呈现抛物线形。
(3) 在靠近开挖面附近的拱顶和仰拱底区域,围岩接触力只有径向接触力降低而无环向接触力升高,表明该区域围岩自重荷载不能通过压力环自身承载,只能通过颗粒间的粘结力承担。而岩土材料的粘结能力有限,故该区域已出现失稳坍塌。进而通过已有文献研究成果,定义该区域为准塌落区域,其边界为压力拱的内边界。
4.3 压力拱随埋深的变化特点研究
压力拱是当前判定隧道深浅埋的重要依据。根据文献[2]对压力拱的定义,压力拱是力的传递路径发生偏转,应力集中的区域。可见压力拱是隧道开挖后的主要承载围岩。结合本文离散-耦合程序计算结果,目前已确定压力拱的内边界,为了研究压力拱随埋深的变化特点,特定义压力拱应力集中等效区域,即以1.15倍为应力增大系数确定外部边界,以压力拱内边界为内部边界,中间区域定义为压力拱应力集中等效区域。
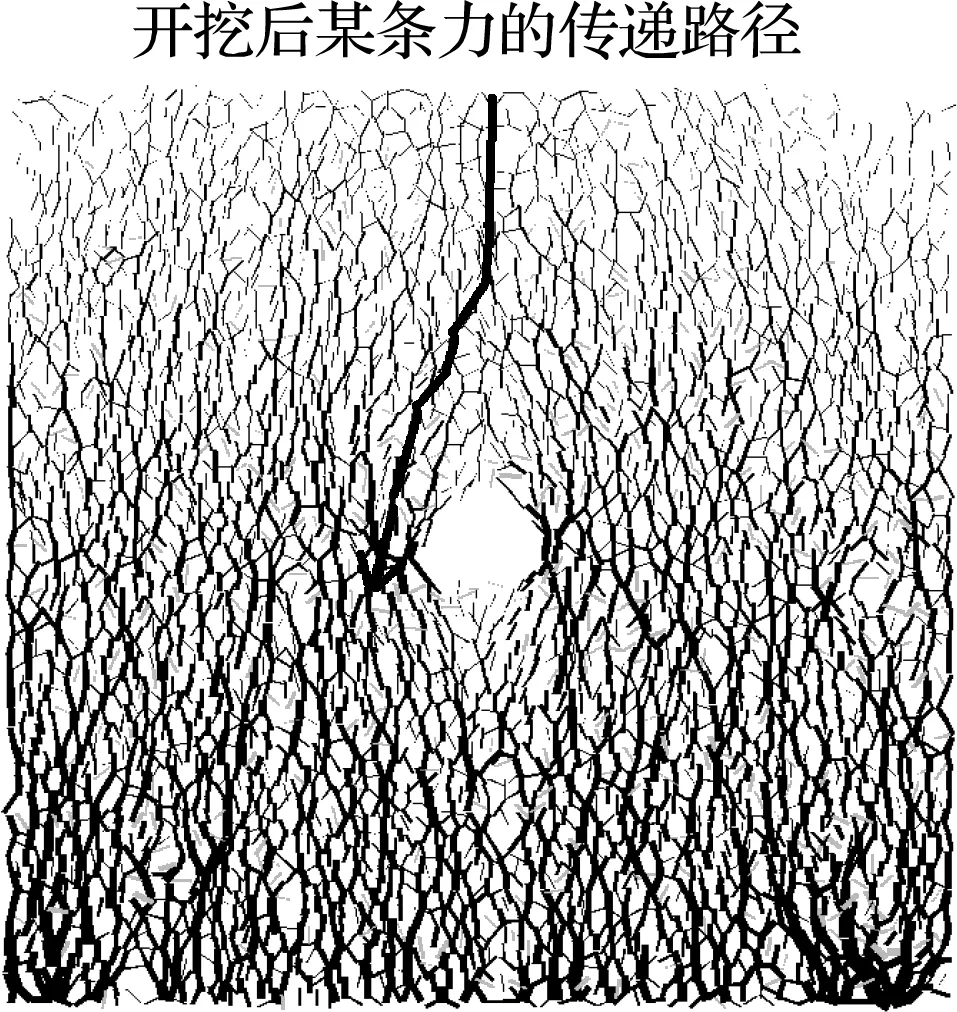
图10 开挖后离散颗粒的力链
Fig.10 Force chain of discrete particles after excavation
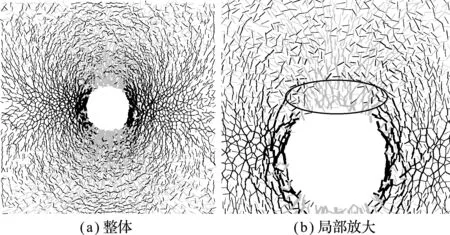
图11 开挖前后接触力变化
Fig.11 Variety of contact force before and after excavation
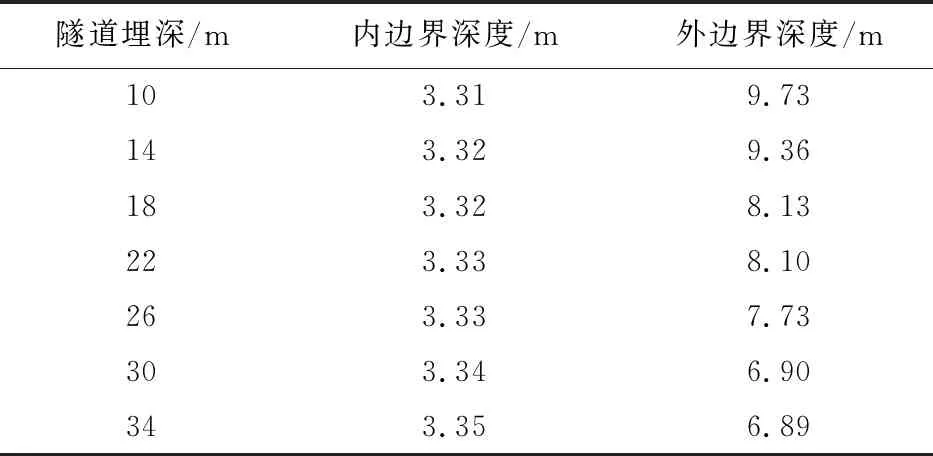
对比计算了埋深分别为10 m,14 m,18 m,22 m,26 m,30 m和34 m情况下的隧道开挖产生的压力拱应力集中等效区域,见图12和表4。
由图12和表4可见,随着隧道埋深的增加,压力拱应力集中等效区域内边界几乎不变,外边界不断变浅,等效区域的面积逐渐减小,可见,随着隧道埋深的增加,隧道周边围岩的压力拱承载能力越来越大;当隧道埋深超过30 m时,压力拱应力集中等效区域随埋深的变化程度减小,表明当埋深达到一定程度后,隧道压力拱高度区域稳定。
表4 不同埋深下的压力拱应力集中等效区域
Tab.4 Stress-concentration equivalent region of pressure arch under different buried depths
隧道埋深/m内边界深度/m外边界深度/m103.319.73143.329.36183.328.13223.338.10263.337.73303.346.90343.356.89
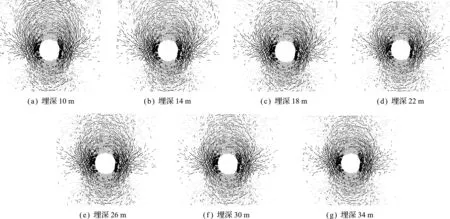
图12 不同埋深下压力拱范围的变化
Fig.12 Variation of region of pressure arch under different buried depths
5 结 论
本文采用二维颗粒流程序PFC2D,基于离散-连续耦合方法对隧道开挖后的围岩受力特性进行了模拟,从微观角度分析了围岩压力拱形成机理及发展规律,得到结论如下。
(1) 基于现有离散-连续耦合程序,提出通过把一定范围的离散颗粒的平均应力作为外荷载的形式施加到有限单元上的方法实现离散-连续之间的耦合;平均应力计算区域面积通过在接触单元的相邻位置放置测量圆来确定,其直径按照该单元的最大边长取值;耦合程序遍历颗粒过程通过将离散颗粒半径进行放大,并且只遍历连续单元附近三层的颗粒的方法降低计算耗时。
(2) 通过优化的离散-连续耦合程序对隧道开挖后的围岩受力特性计算结果可见,开挖面周边范围出现层状压力环,但在拱顶和仰拱底附近区域的围岩压力环的环间接触力降低,围岩承载能力急剧降低,力向深部围岩传递,导致浅部围岩容易出现失稳,甚至发生塌落,形成压力拱。
(3) 随着隧道埋深的增加,隧道周边围岩的压力拱承载能力越来越大;但当隧道埋深达到一定界限后,隧道压力拱高度趋于稳定。
本文主要研究了离散-连续耦合模型在隧道压力拱研究中的可行性,该耦合程序既提高了计算效率,又能从微观角度研究围岩失稳机理。但耦合程序的参数直接影响计算结果的精度。因此,在下一步研究中应结合隧道工程特点及围岩特性,加强对离散部分材料及耦合边界参数的研究。
