基于傅里叶级数的汽轮机叶根轮槽结构设计
2020-05-22张小娟余德启舒伟林
李 明,张小娟,余德启,舒伟林,程 凯
(1.大连理工大学 工业装备结构分析国家重点实验室,大连 116024;2.上海汽轮机厂有限公司 上海电气,上海 200240)
1 引 言
汽轮机作为重要的旋转动力机械,广泛应用于能源和运输行业。随着社会进步和技术发展,汽轮机面临更加恶劣的工作环境和更高的工作性能要求,易在运行时发生失效和破坏,从而造成发电机组可靠性的丧失,产生重大经济损失。叶根是汽轮机中将叶片受力传递至轮槽转子的关键部件,其几何尺寸一般较小。超高转速产生的巨大离心力作用于叶根部位,会引起较高的应力水平和叶根的失效破坏,从而影响发电汽轮机的可靠性和经济效益。通过选用高强度材料来提升叶根强度的空间有限,并会带来成本的上升,通过优化叶根结构以降低应力分布水平,提高疲劳寿命,具有重要的意义。
张明辉等[1-3]使用圆弧-直线法(圆弧曲线与直线结合)参数化建模表征枞树型叶根与轮槽型线,以几何参数为优化变量,通过最小化峰值等效应力给出优化构型。Song等[4]基于圆弧和直线参数化表征枞树形叶根,以最小化轮槽峰值应力和最大化前缘面积为优化目标。Rao等[5-7]使用圆弧表征叶根齿型,用直线表征叶根接触面,以最小化峰值应力为目标函数,开展叶根型线形状优化。邢誉峰等[8]将枞树型榫槽看作圆弧和直线的组合体,以半径和定位尺寸等几何特征参数为设计变量,考虑几何连续和尺寸约束,以轮缘峰值应力最小化为优化目标,达到了提高使用寿命和降低成本的目的。Yu等[9]开发优化设计平台,基于圆弧-直线法和加权峰值应力最小化策略,自动生成和优化叶根轮槽型线。
已有汽轮机叶根轮槽优化设计的工作系统理性考虑结构设计对应力分布的影响,与费力耗时的经验试错法相比,具有高效和经济的优点,促进了汽轮机的设计与发展,但也存在着一定的不足。(1) 叶根轮槽构型的数学描述。针对枞树型叶根,基于圆弧直线组合的方法受限于圆弧特征假设和连续性条件,无法描述超椭圆[10]等复杂曲线,限制了叶根轮槽优化空间。(2) 优化目标的选取。已有工作多定义最小化峰值应力为优化目标,构建典型的min-max优化问题。但这种优化目标定义具备高度非线性,优化过程中易出现峰值应力位置波动,造成优化迭代震荡和不收敛问题,使得优化代价较高[11]。
本文以工程三齿枞树型叶根轮槽为例,采用具有描述复杂几何形状能力的傅里叶级数与直线相结合的方法来表征枞树型叶根轮槽型线,拓宽结构优化的搜索空间。利用KS函数凝聚应力值,有利于降低目标函数的非线性程度,确保优化快速收敛。与圆弧-直线法和最小化峰值应力的优化结果进行比较,验证了傅里叶级数-直线法和KS凝聚应力法的有效性。
2 枞树型叶根轮槽的构型描述
傅里叶级数具有光滑性、对称性和周期性[12],在表征复杂曲线方面,具有高保真度、完备性和复杂构型描述能力。基于傅里叶级数-直线法的枞树型叶根轮槽构型描述如图1所示。整个型线由一个傅里叶级数构成,在相邻拐点之间三点近似共线部分用直线代替以表征摩擦接触。为了契合工程实际,不同接触段直线的斜率保持一致。
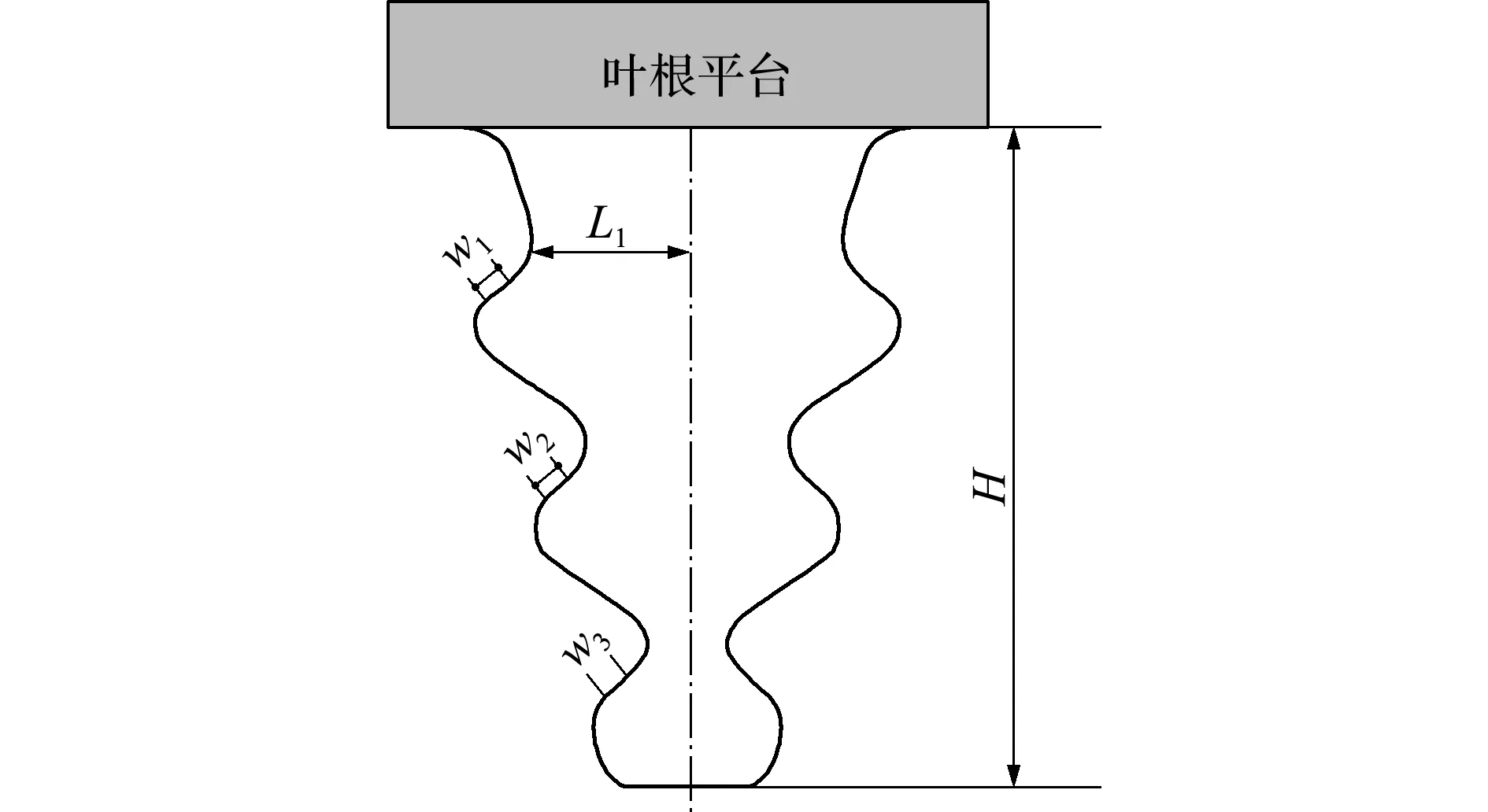
图1 基于傅里叶级数-直线法的枞树型叶根描述
Fig.1 Illustration of fir-tree root characterization through Fourier series -line method
傅里叶级数的数学表达为
(1)
式中M,αn,βn,l和α0分别为傅里叶级数的阶次、余弦项系数、正弦项系数、周期和常数项。傅里叶级数-直线法描述构型的保真度可用决定系数R2表征。决定系数表达式为
(2)
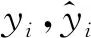
基于圆弧-直线法的枞树型叶根轮槽构型描述如图3所示,每个齿均由四个圆弧和两条直线组成。圆弧间的相切条件是xj=xi+(Rj-Ri)cosθb和yj=yi+(Rj-Ri)sinθb。直线与圆弧相切条件为xi=xk-Risinθa和yi=yk+Ricosθa,其中,(xi,yi)和(xj,yj)分别是半径Ri和Rj的圆心坐标,(xk,yk)是圆弧与直线的切点,θa和θb分别是斜线和直线段倾角。为减少设计变量数目,假设接触段的中心点位于一条直线上,圆弧的半径、圆心和型线上的切点均可由设计变量计算确定。
3 枞树型叶根轮槽的优化设计
汽轮机枞树型叶根轮槽优化设计调用有限元应力分析来评估设计构型的优劣。本文基于Python语言,调用商业软件ABAQUS进行应力有限元分析。出于计算效率考量,忽略沿深度方向的偏心扭转效应,将三维枞树型叶根轮槽简化为二维平面应变结构。边界条件为,(1) 轮槽两侧为循环对称边界条件;(2) 接触面摩擦系数为0.15;(3) 固定轮槽底端表征转子与轮槽间嵌套效果。汽轮机运行中产生的离心力作用于叶根平台。为保证网格精度,在叶根轮槽表面指定有限厚度的缓冲层设置四边形高阶网格,每个齿对应的单元数目均不少于20,其他非敏感区域采用粗糙网格。采用CPE4I单元避免剪切自锁现象。
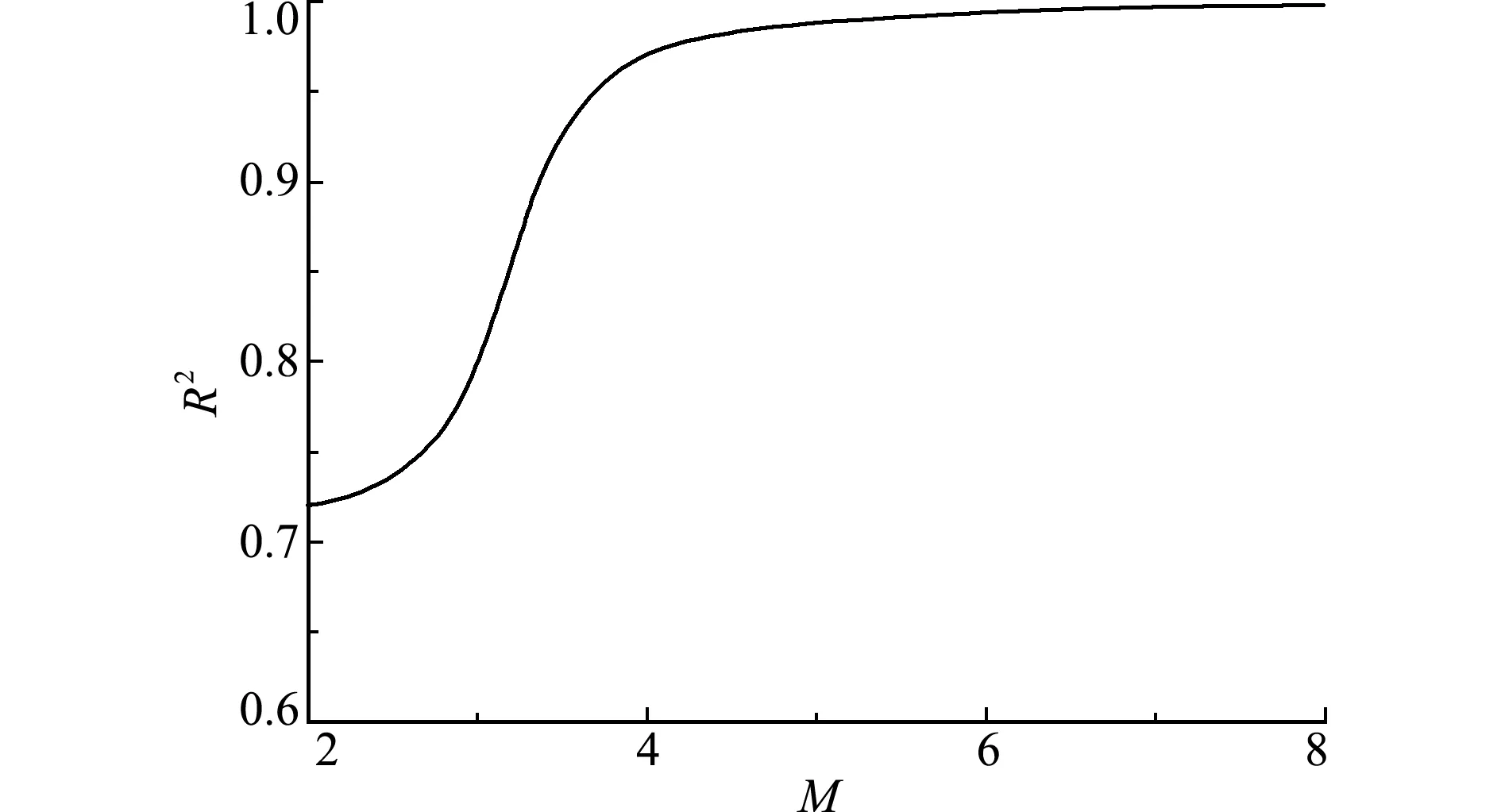
图2 不同阶次傅里叶级数拟合的决定系数
Fig.2 Coefficient of determination for numerically fitting with Fourier series of different orders
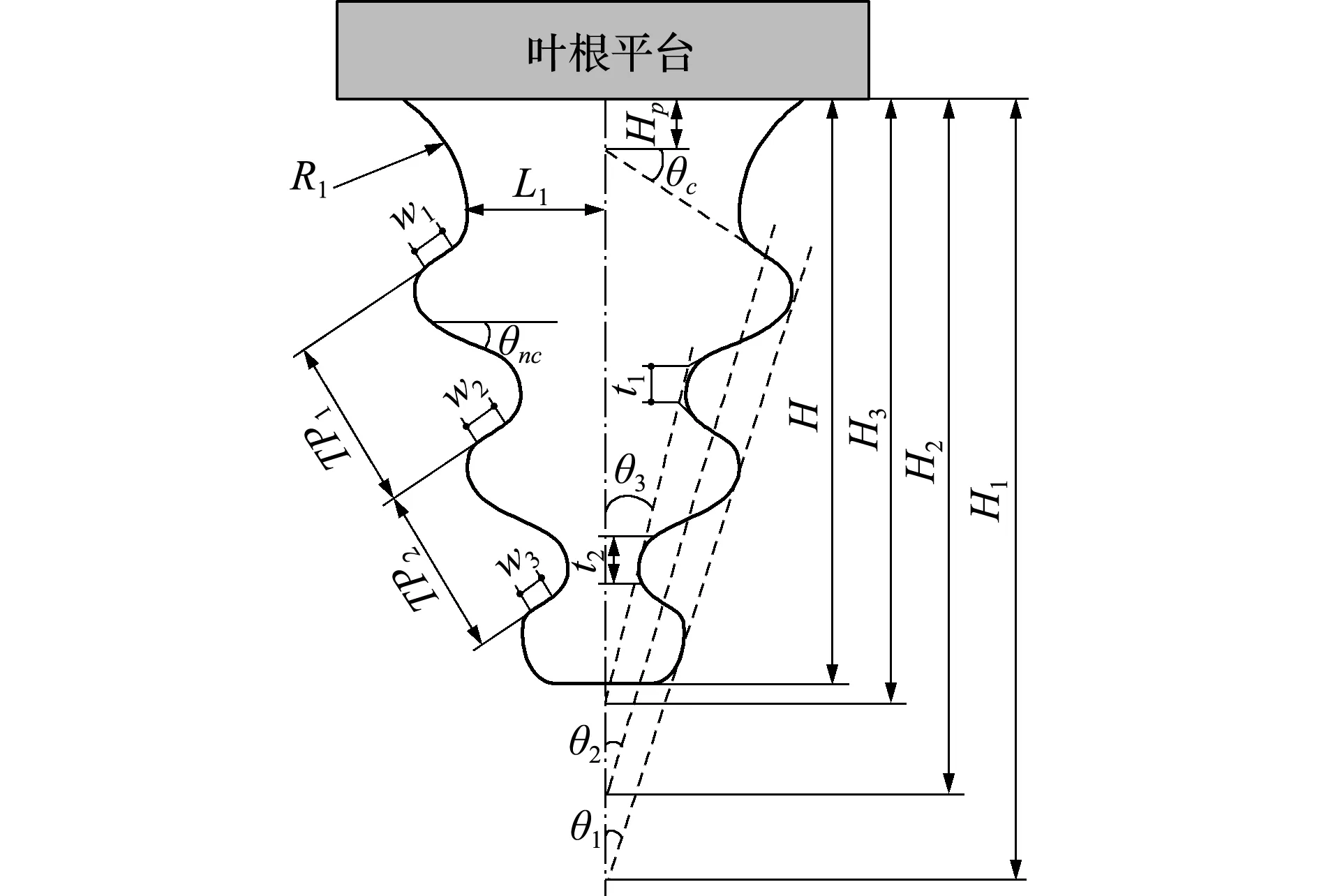
图3 基于圆弧-直线法的枞树型叶根描述
Fig.3 Illustration of fir-tree root characterization through arc-line method
优化设计中,为避免最小化峰值应力引起的收敛震荡迭代,引入KS凝聚函数
(3)
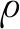
以工程三齿枞树型叶根轮槽为例,使用傅里叶级数-直线法和最小化KS凝聚应力值开展优化设计。为了验证方法的有效性,同时也使用圆弧-直线法和最小化峰值应力策略进行三齿枞树型叶根轮槽的结构设计。
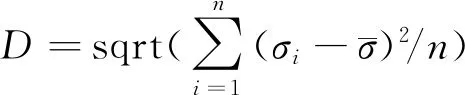
(4)
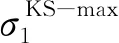
圆弧-直线法叶根轮槽构型描述对应的设计变量为倾斜角θi、接触面倾斜角θc、非接触面倾斜角θn c、位置高度Hi、叶根高度H、接触面宽度wi、齿间距TPi、第一齿接触面位置高度Hp和齿面厚度ti和圆弧半径R1。因此,基于圆弧-直线法和最小化峰值应力值的优化列式为
(5)
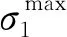
优化设计基于商业软件Isight,采用多岛遗传算法[14,15]。优化参数设置种群数、岛屿数、代数、交叉率、突变率、迁移率和迁移间隔分别为10,5,200,1.0,0.01,0.01和5。
4 结果与讨论
4.1 确定傅里叶级数阶次
如图2所示,决定系数变化趋势表明,为准确拟合叶根轮槽型线,傅里叶级数阶次M应不小于4,但过大的M值易引起过拟合现象。本文基于不同M值进行优化迭代,以40代为例,如图4所示,当M小于6时,叶根轮槽峰值应力变化平缓;当M值大于6时,产生过拟合现象,峰值应力急剧上升,优化效果差。因此,综合考虑精度和效率、过拟合与欠拟合问题,本文选定傅里叶级数阶次M=4。
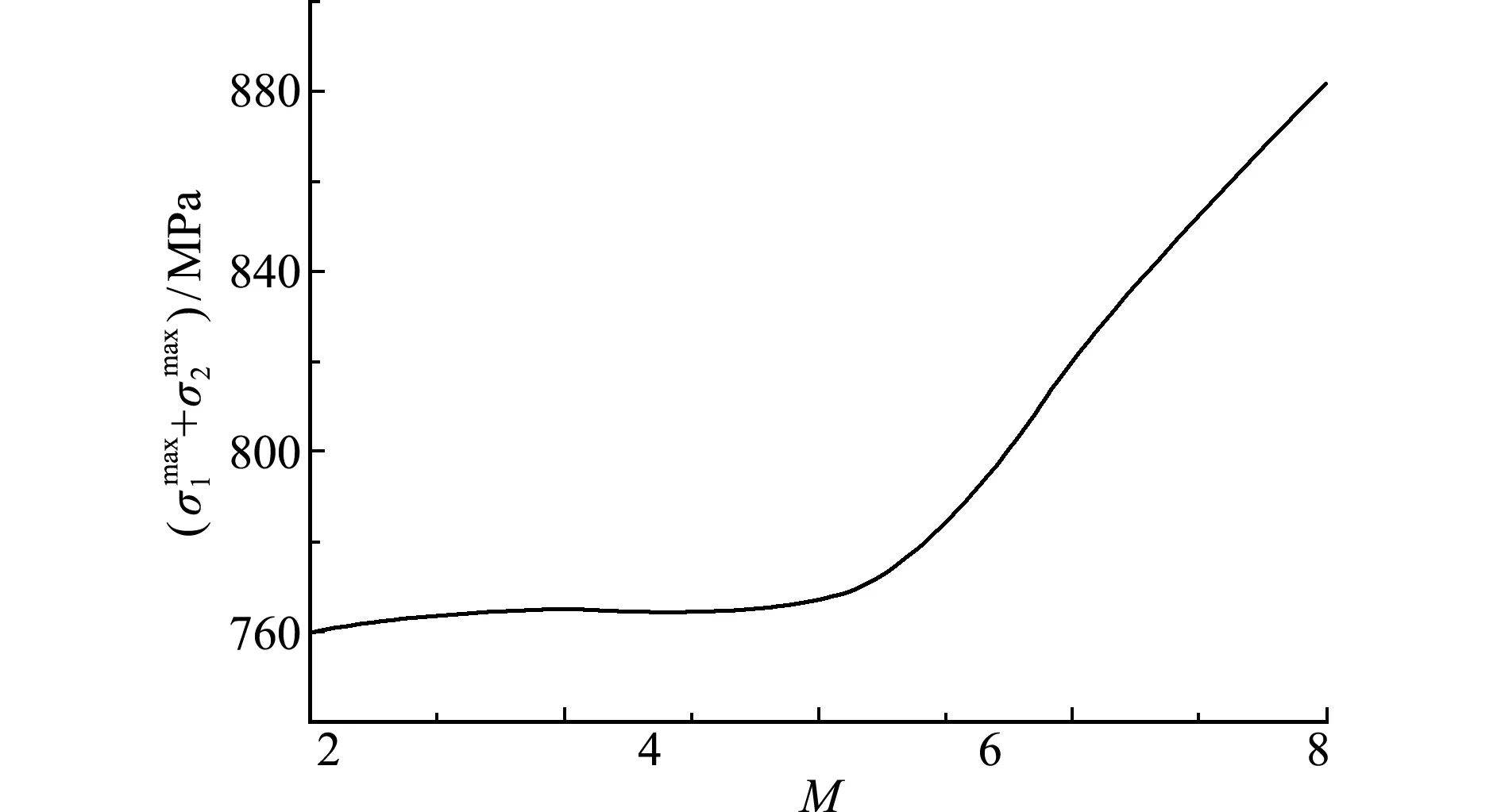
图4 基于不同阶次傅里叶级数-直线法的优化峰值应力
Fig.4 Optimized peak stresses of based on Fourier series -line method with different orders
4.2 优化结果
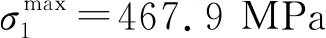
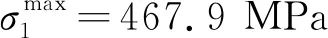
本文比较基于傅里叶级数-直线法和最小化KS凝聚应力值优化策略与基于圆弧-直线法和最小化峰值应力优化策略的优化结果,分析两种方法的优劣。由图5和图7对比可知,最小化KS凝聚应力值的优化策略在第80代开始收敛, 而最小化峰值应力的优化策略在第150代开始收敛,证明KS函数可以减少迭代震荡,加快迭代收敛速度;对比图6(a)和图8(a)可知,与初始构型相比,傅里叶级数-直线法以较小的构型改变即可找到最优解,而圆弧-直线法则需要较大的构型改变方可得到优化构型,表明在相同条件下,傅里叶级数-直线法能描述更多的构型,保证优化可行解的完备性;对比图6(b)和图8(b)可知,与圆弧-直线法相比,傅里叶级数-直线法给出的优化构型对应的峰值应力值较小,优化效果较好。

图5 傅里叶级数-直线法和最小化KS凝聚应力值的优化迭代历史
Fig.5 Iteration history for Fourier series -line method and minimization of KS aggregation for stress values based optimization
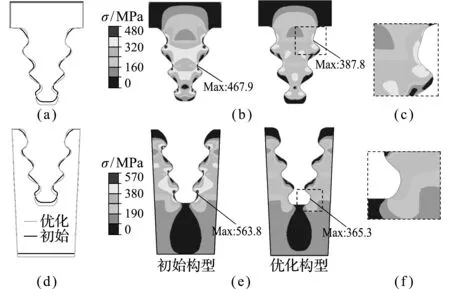
图6 基于傅里叶级数-直线法和最小化KS凝聚应力值的优化结果
Fig.6 Optimal results of the Fourier series -line method and mini-mization of KS aggregation for stress values based optimization
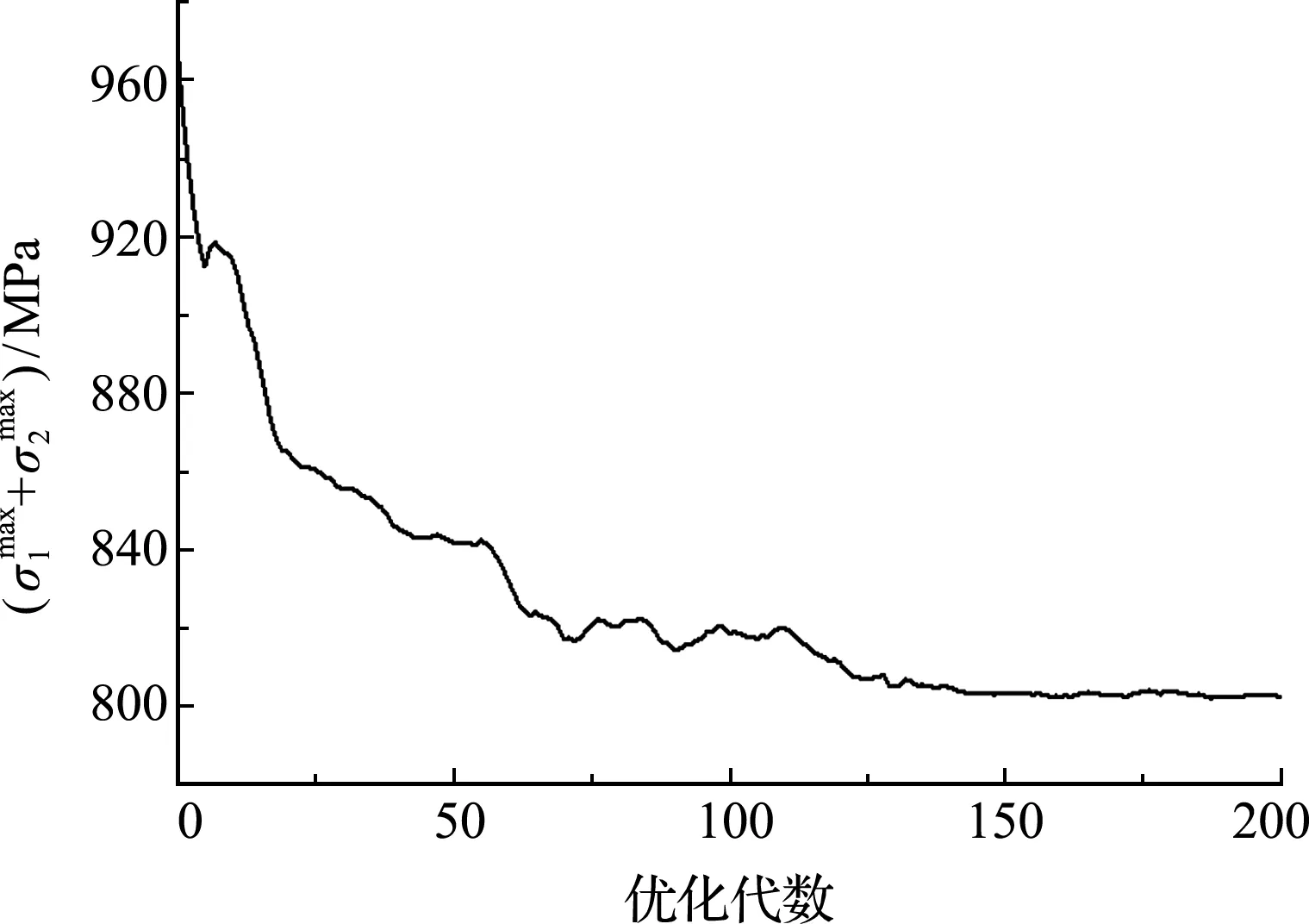
图7 基于圆弧-直线法和最小化峰值应力的优化迭代历史
Fig.7 Iteration history for arc-line method and minimization of peak stress based optimization
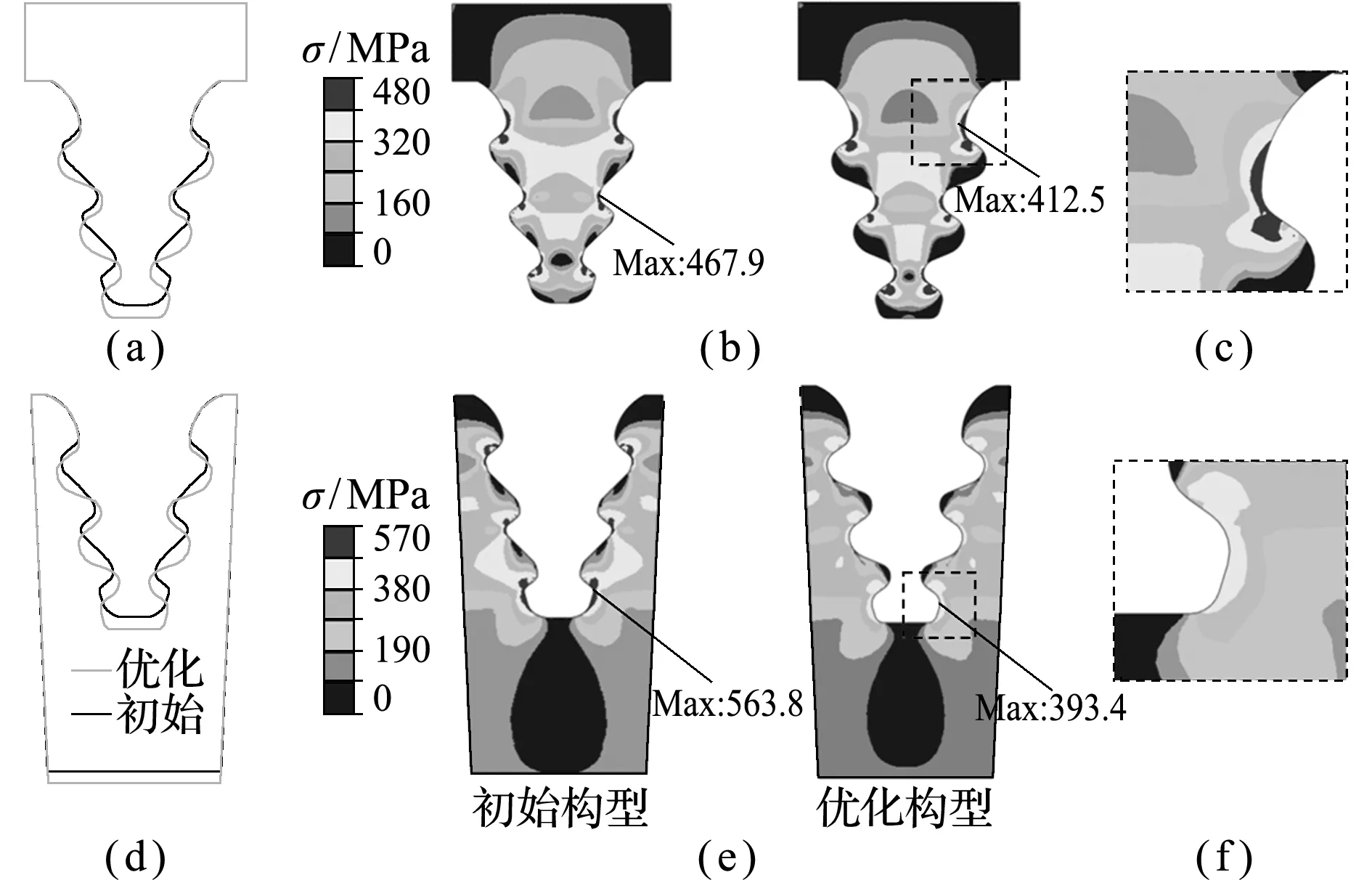
图8 基于圆弧-直线法和最小化峰值应力的优化结果
Fig.8 Optimal results of the arc-line method and minimization of peak stress based optimization
5 结 论
针对枞树型叶根轮槽的优化设计,本文基于傅里叶级数-直线法表征叶根轮槽构型,以最小化KS凝聚应力值为优化目标,与基于圆弧-直线法和最小化峰值应力优化策略相比较,得出的结论如下。
(1) 与基于圆弧-直线法相比,基于傅里叶级数-直线法具有更宽广的优化搜索空间和更精准描述构型的能力。
(2) 与最小化峰值应力优化策略相比,最小化KS凝聚应力值可以有效地保证优化快速收敛。
(3) 与初始构型相比,基于傅里叶级数-直线法优化的叶根与轮槽峰值应力分别下降17.12%和35.21%,基于圆弧-直线法优化的叶根与轮槽峰值应力分别下降11.84%和30.22%。基于傅里叶级数-直线法的优化效果较明显。
