基于自然单元法的轴对称结构极限上限分析
2020-05-22陈莘莘
陈莘莘,王 崴
(华东交通大学 土木建筑学院,南昌 330013)
1 引 言
作为塑性力学最具实用意义的分支之一,结构极限分析的目的是确定工程结构的极限荷载[1]。结构极限分析一般不需要知道载荷变化的历史,相对于传统的弹塑性增量分析往往效率更高更适用。虽然极限分析的数值方法[2-4]得到了迅速发展,但发展高效准确和切实可行的极限分析数值方法仍是当前研究的热点。
作为一种新颖而独特的数值计算方法,无网格法[5]近似函数不依赖于网格,且在节点不规则分布时,不会损失多少计算精度,从而日益得到重视,并得到不断发展。目前,无网格法的种类已十分繁多,比较典型的有无单元伽辽金法[6,7]、重构核粒子法[8]、无网格局部Petrov-Galerkin法[9]和自然单元法[10,11]等。其中,发展较晚的自然单元法是一种以自然邻近插值作为试函数,以Galerkin法作为加权残量法而得到的新型无网格方法。与大多数无网格法不同,自然单元法的形函数具有插值性且在边界节点间是线性变化的,从而可以直接施加本质边界条件。此外,自然单元法的形函数构造简单,不涉及复杂的矩阵求逆运算,更不需要任何人为的参数。盖珊珊等[12]提出了线弹性断裂问题的自然单元法。董轶等[13]将应力杂交的思想引入自然单元法中,提出了弹性力学问题的杂交自然单元法。丁道红等[14]提出了材料非线性问题分析的自然单元法。周书涛等[15]提出了平面问题极限上限分析的自然单元法。但目前尚未见到自然单元法针对轴对称结构极限上限分析的研究成果。
本文根据极限分析上限定理,详细推导了轴对称结构极限上限分析的自然单元法求解格式,并编制了相应的计算程序。通过典型算例的计算和对比分析,验证了所提轴对称结构极限上限分析方法的有效性和合理性。
2 无网格自然单元法
无网格自然单元法是采用自然邻近插值构造函数近似空间的一种新型数值方法,具有不依赖网格的优势,同时形函数构造简单,且在边界上满足插值性质。自然邻近插值按插值基函数的不同可分为Sibson插值[16]和Laplace插值[17]。
2.1 Voronoi结构和Delaunay三角形
设平面中有一点集N={x1,x2,x3,…,xN},则任意点xi的一阶Voronoi 结构实际上是以点xi为最近离散点的空间位置的集合,其数学表达式为
Ti={x∈R2d(x,xi)≤d(x,xj),∀j≠i}
(1)
二阶Voronoi结构Ti j表示以xi为最近点,以xj为次近点的空间位置的集合,其数学表达式为
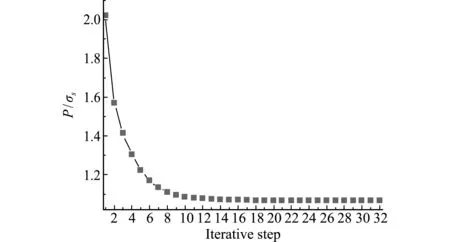
Ti j={x∈R2d(x,xi) ∀j≠i≠k} (2) 图1所示为平面7个节点的一阶Voronoi结构和待插点x的二阶Voronoi结构。作为Voronoi结构的对偶,Delaunay三角化是把有公共Voronoi结构边界的节点连接起来将整体域划分成三角形区域。Delaunay三角形的一个重要特性是每个Delaunay三角形的外接圆中无任何其他节点,即空圆准则,常用于确定计算点的自然邻近点。 图1 点x的一阶和二阶Voronoi结构 Fig.1 First-order and second-order Voronoi cells aboutx 设插值点x的一阶Voronoi结构Tx和二阶Voronoi结构Tx i的面积分别为A(x)和Ai(x),则插值点x的形函数及其导数为[16] (3) (4) 定义了各节点的插值函数后,位移场函数u(x)可写为 (5) 式中ui表示点x周围n个自然邻近点的节点位移。 (6) (7) ui,i=0, inV (8) ui=0, onΓu (9) 式中σs表示材料的屈服应力,εi j表示应变率。为了简便起见,通常将位移速度场和应变率分别称为位移和应变。 将轴对称面Ω离散成N个任意分布的节点,则应变矩阵ε可以写为 ε=BU (10) 式中U为节点位移列向量,且 (11) (12) 对于轴对称问题,有 εi jεi j=εTDε=UTBTDBU=UTKU (13) 式中 (14) 根据式(13),目标函数(6)可离散为 (15) FTU=1 (16) 式中F为等效载荷列向量。不可压条件(8)可表示为 ui,i=εr+εz+εθ=BcU=0 (17) 式中 (18) (19) 进一歩,式(17)可以表达为 (εr+εz+εθ)2=UTKcU=0 (20) (21) 经过上述推导,离散化的轴对称结构极限上限分析的数学规划格式为 (22) s.t.FTU=1 (23) UT(Kc)iU=0 (i∈I) (24) 采用拉格朗日乘子法将归一化条件引入到目标函数中,则式(22~24)所表示的数学规划问题可写为 (25) s.t.UT(Kc)iU=0 (i∈I) (26) 式中q为拉格朗日乘子。根据式(25,26)的极小化条件,可得 (27) FTU=1 (28) UT(Kc)iU=0 (i∈I) (29) 式(27)成立的前提是对每个积分点都有 UTKiU≠0 (i∈I) (30) 为便于求解式(27~29)所示的非线性方程组,构造如下的迭代格式, (31) FTUk=1 (32) (33) 式中Uk和qk分别表示第k迭代步的节点位移向量和拉格朗日乘子,Uk - 1是第k-1迭代步的节点位移向量。然而,当某些积分点上的应变为0时,式(31)是没有意义的。因此,在进行第k歩迭代前,需将全部积分点分为刚性区子集Rk和塑性区子集Pk: I=Pk∪Rk (34) (35) (36) 综上所述,极限上限分析的离散数学规划格式可表达为 (37) s.t.FTUk=1 (38) (39) (40) 采用拉格朗日乘子法和罚函数法分别将式(38~40)引入到目标函数后,式(37~40)的数学规划格式可以等效成易求解的极小化问题: (41) 式中α和β为罚因子,通常取104~108可得到较高的计算精度[15]。根据以上构想,极限上限分析的迭代算法可归纳为 第0步:假设初始状态下整个结构无刚性区,求解如下的极小问题, (42) s.t.FTU0=1 (43) (44) 通过求解以上的极小化问题,可得到初始的极限载荷乘子为 (45) 第k步:根据第k-1步的位移向量Uk - 1确定刚性区子集Rk和塑性区子集Pk,并求解如下极小化问题, (46) s.t.FTUk=1 (47) (48) (49) 通过求解以上的极小化问题,可得到第k歩的极限载荷乘子为 (50) 对于预先给定的误差容限ε,如果满足 (51) 则迭代终止。本文误差容限取ε=2.0×10-4。 考虑一受均布内压P作用的厚壁圆筒,其内半径为a,外半径为b,其极限载荷解析解为[1] (52) 对于不同的b/a,采用不同的节点布置方案进行计算,图2给出了b/a=2时的节点布置方案。 图2b/a=2时厚壁圆筒的节点布置 Fig.2 Nodal distribution for a thick-walled cylinder whenb/a=2 图3给出了厚壁圆筒极限载荷的本文数值解和解析解的比较。显然,本文数值解与解析解吻合很好,说明本文方法的计算精度较高。 图3 厚壁圆筒极限载荷数值解与解析解的比较 Fig.3 Numerical limit loads compared with analytical solutions for the thick-walled cylinder 为进一歩验证本文方法的有效性,考虑一受均布内压P作用的厚壁球壳,如图4所示,其内外半径分别为a和b,其极限载荷的解析解为[1] 图4 厚壁球壳 Fig.4 A thick-walled spherical shell P=2σsln (b/a) (53) 此问题是球对称问题,现将其作为轴对称问题进行求解。对于不同的b/a,采用不同的节点布置方案进行计算。图5给出了b/a=1.3时,厚壁球壳的节点布置方案。图6给出了b/a=1.05~1.3时,厚壁球壳的极限载荷数值解和解析解的比较。显然,本文数值解和解析解吻合很好。 图5b/a=1.3时厚壁球壳的节点布置 Fig.5 Nodal distribution for a thick-walled spherical shell whenb/a=1.3 图6 厚壁球壳极限载荷数值解与解析解的比较 Fig.6 Numerical limit loads compared with analytical solutions for the thick-walled spherical shell 本算例考虑一个圆柱-圆锥形组合筒,结构的尺寸和受载情况如图7所示,这也是一个轴对称问题。 图7 圆柱-圆锥组合筒 Fig.7 Cylindrical-conical combined cylinder 采用图8所示的节点布置方案计算得到了该组合筒顶部均布荷载P的极限载荷为1.065σs。图9 给出了极限上限分析的迭代收敛示意图,可以看出,本文算法具有较好的收敛性。 图8 圆柱-圆锥组合筒的节点布置 Fig.8 Nodal distribution for a cylindrical-conical combined cylinder 图9 圆柱-圆锥形组合筒的极限上限分析迭代过程 Fig.9 Iterative process for upper bound limit analysis of the cylindrical-conical combined cylinder 无网格自然单元法不需要对求解域进行网格划分,同时本质边界条件的施加十分方便,是一种兼具了有限元法和无网格法优点的数值方法。本文根据极限上限分析定理,采用自然邻近插值构造轴对称结构的位移场,并通过将积分点划分为刚性区和塑性区子集的办法克服目标函数非线性且不可微的困难,建立了轴对称结构极限上限分析的自然单元法。本文的数值计算结果表明,采用自然单元法进行轴对称结构的极限上限分析是可行的,具有前处理方便、稳定性好和精度高等优点。本文方法不仅推广了自然单元法的应用范围,而且对拓展轴对称结构极限上限分析的数值方法有着积极的意义。
2.2 Sibson插值

3 无搜索迭代算法


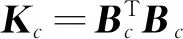
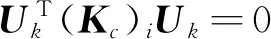

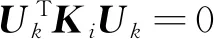
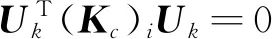
4 数值算例
4.1 厚壁圆筒
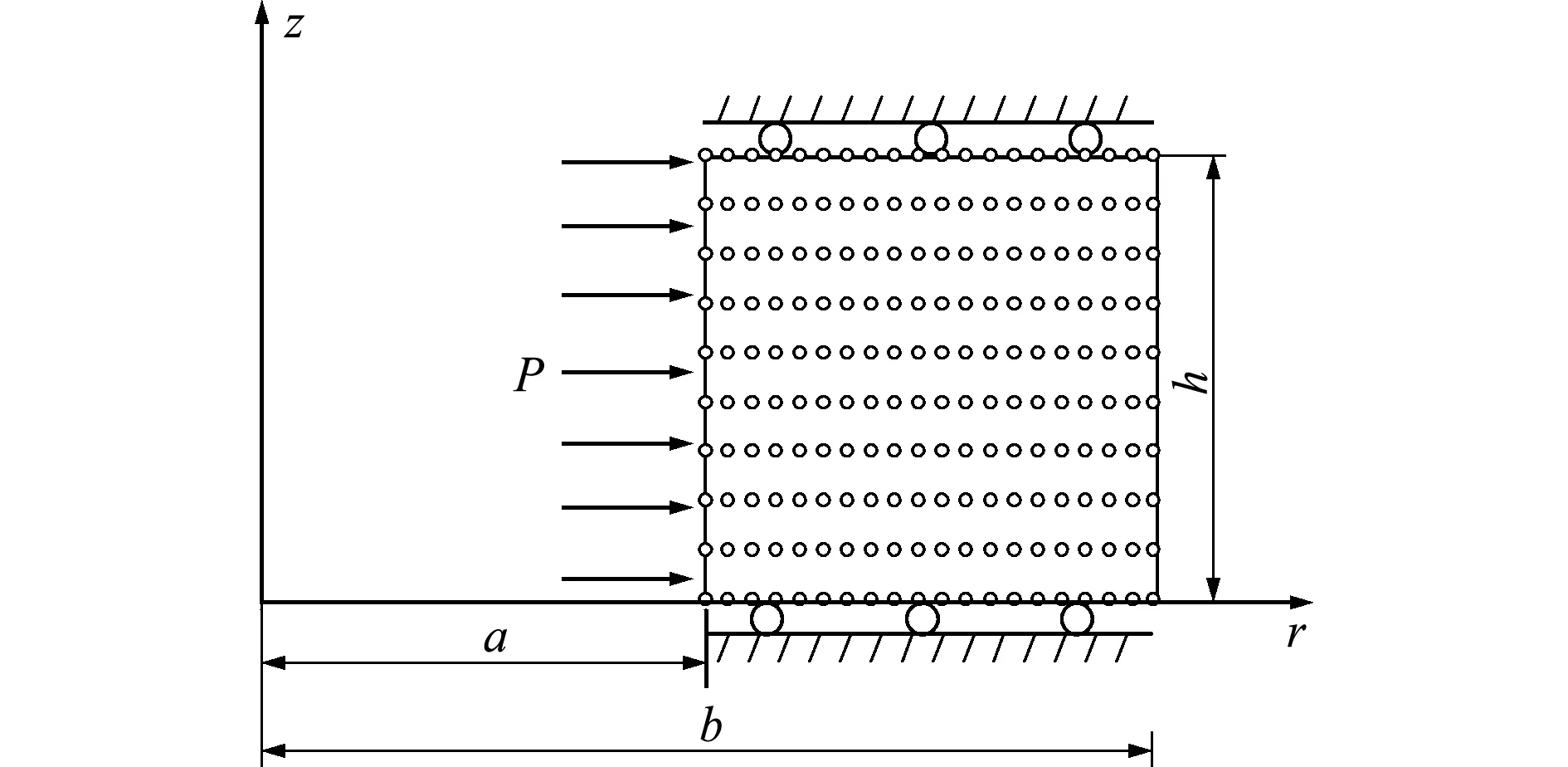
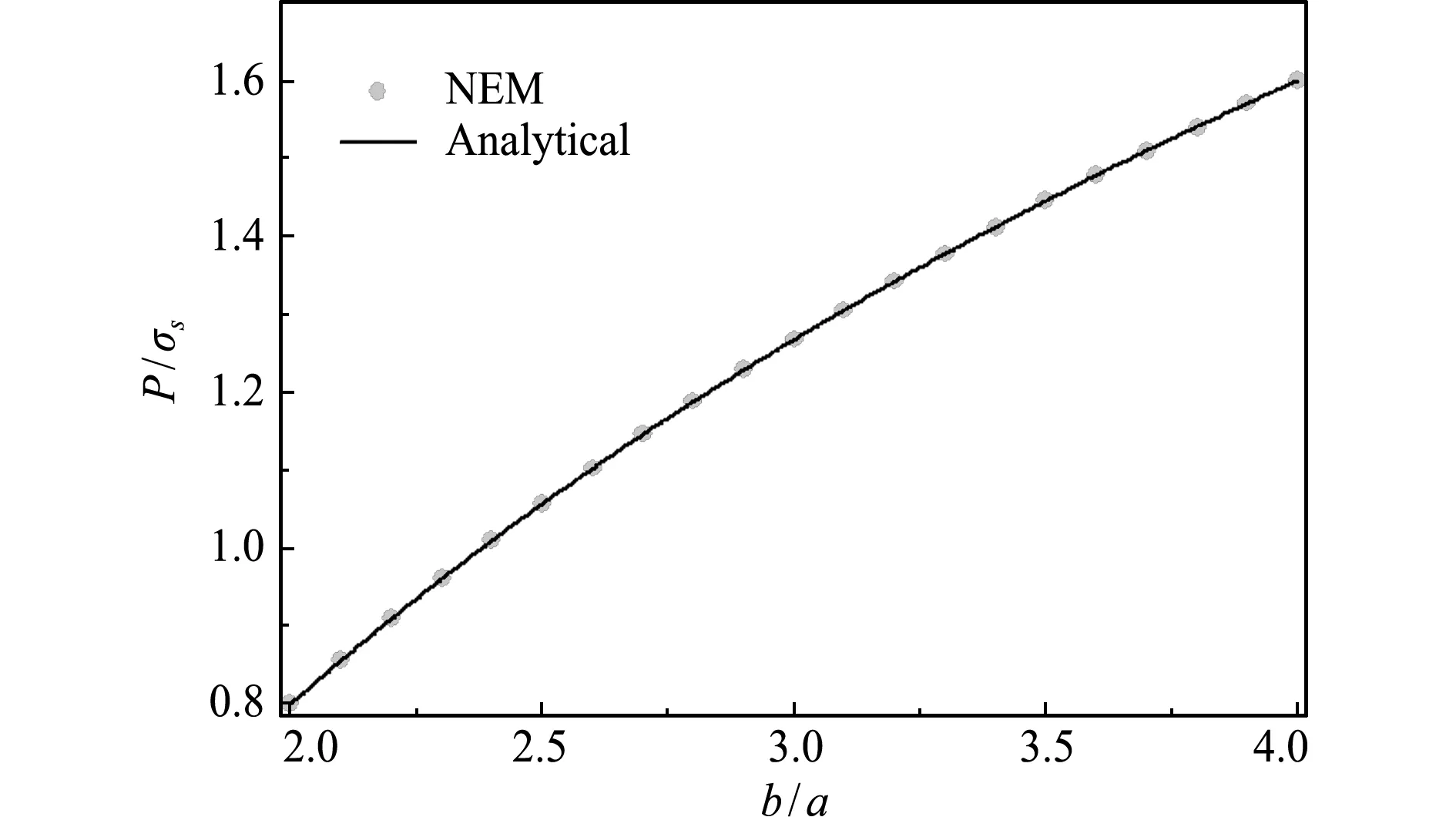
4.2 厚壁球壳
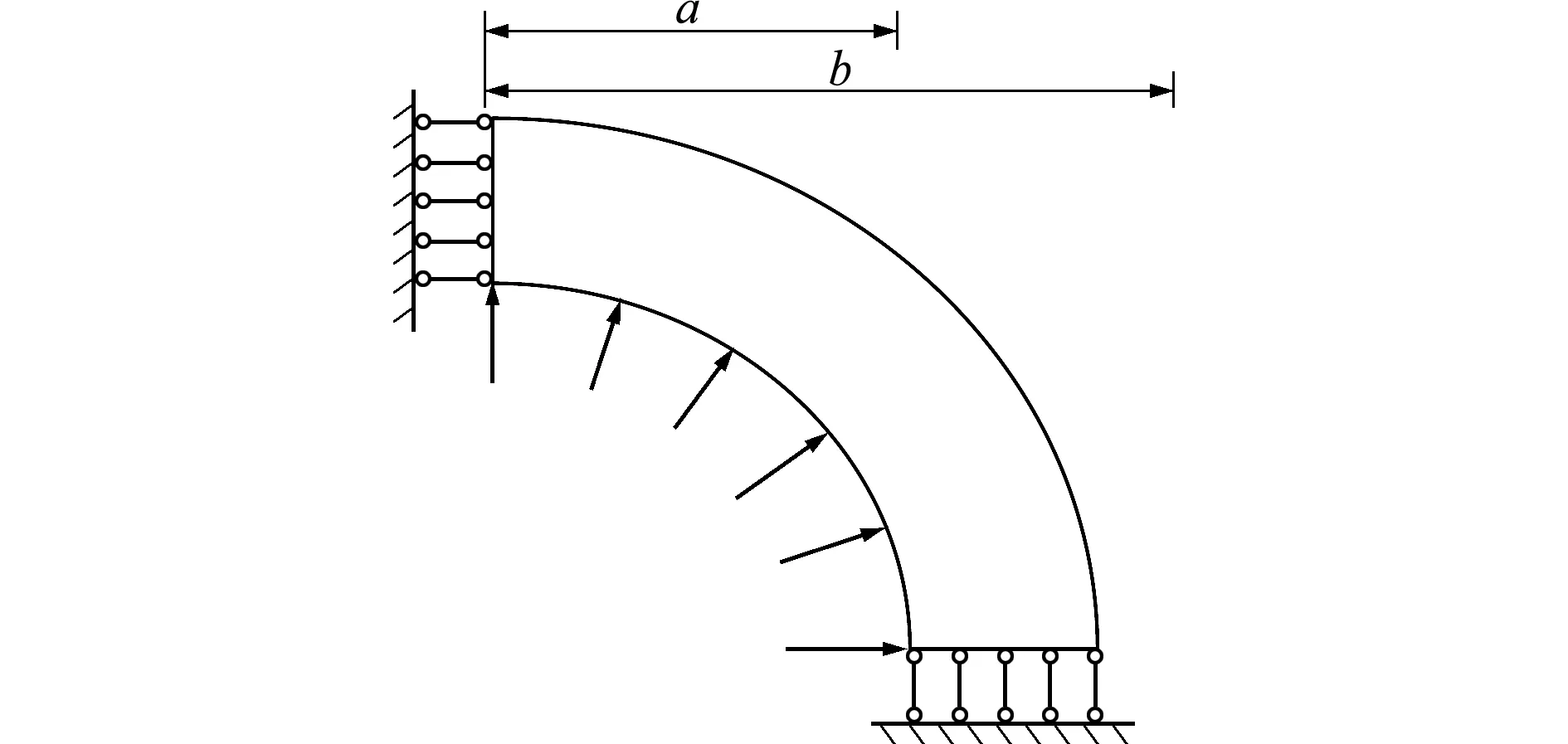
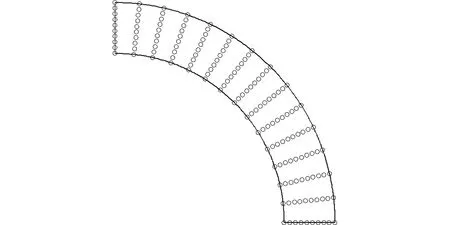

4.3 圆柱-圆锥形组合筒


5 结 论
