解题教学中观察能力的培养:意义、策略与路径
2020-03-27周锦春
周锦春
[摘 要] 观察能力的培养不仅关系到教学目标的实现,而且关系到数学核心素养的发展,同时对教学效率的提高也具有非常重要的意义. 在解题教学中,观察能力的培养需从学会观察题目特点开始,从多角度观察出发,从动态与静态观察相结合展开,从学会观察隐含条件出发,从类比观察中得以提升.
[关键词] 解题教学;观察能力;培养;核心素养
数学中的观察能力是一种高级思维活动,是指主动观察事物或者现象,对事物的特征与差异具有一定的认识的能力. 心理学研究显示,观察能力是学生学习的必备条件,同时也是智力发展的有效载体. 观察能力有先天具备和后天培养之分,先天条件是可遇不可求的,而后天的培养则是在于教师的引导和自身的体会. 因此,培养学生的观察能力是解题教学中的一项长期任务. 本文拟对解题教学中观察能力培养的意义、策略以及具体路径进行探讨,以期引起大家对观察力培养的关注与研究.
观察能力培养的意义
1. 实现教学目标需要
观察能力是学习数学的基石,是看清数学思想的明眸,是实现教学目标的需要. 抽象数学概念的获取,需要学生观察其本质;一些算法的理解,需要学生观察其算理;理解能力的提升,也需要学生观察其中的解题策略;一些数学问题的分析,也需要学生观察其规律,观察能力也是数学课程的培养目标之一.
2. 核心素养发展的需要
普通高中数学课程标准提出:提高学生的数学素养,引导学生会用数学眼光观察世界……高中阶段要实现以上“三会”的目标离不开观察力,数学与现实生活的关联并非一望而知的,需要学生有观察数学与现实生活关联的能力. 因此,观察能力无疑是学生核心素养发展的需要.
3. 提高教学效率的需要
当下,高中教学中依然存在着教学质量低下的弊端. 而深究低效教学背后的根源自然是多因素的掺杂,不过学生观察能力的薄弱和观察习惯的缺失是其中一个重要因素. 试想一个缺乏观察能力的学生,如何才能发现多种解题策略中的规律?由此可见,学生的低效学习也是显而易见的. 从而培养并发展学生的观察能力对教学效率的提高也具有非常重要的意义.
在解题教学中,观察能力培养的策略与路径
1. 从学会观察题目特点开始
形成解题路径的首要条件是发现数学问题中的内在关联以及规律. 因此,我们应该提倡学生去观察问题的结构特点,联系蕴含其中的那些离散的数学知识与技能,并且引发对解题的深入探究,从而帮助学生形成正确、简洁的解题路径[1].
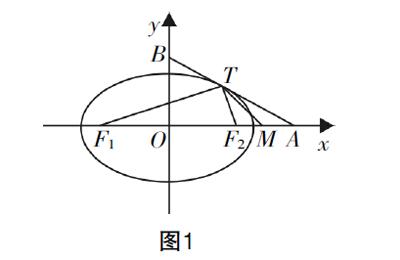
例1:如图1所示,椭圆C: + =1(a>b>0)的离心率e= ,该椭圆与过点A(2,0)和点B(0,1)的直线有且仅有一个公共点.
(1)试求出椭圆C的方程;
(2)设F1为椭圆C的左焦点,F2为椭圆C的右焦点,同时M为线段AF2的中点,证明:∠ATM=∠AF1T.
分析:观察是为了解决问题,而不是胡乱地观察. 本题第(1)问中,通过对图形的深入观察,较易明确解题思路,由直线AB和椭圆C仅有一交点,不难联想到联立方程组、一元二次方程以及根的判别式,得出椭圆方程C:x2+4y2=2. 当然解题思路也是在观察的基础上建立的. 在第(2)问中,观察图1我们易得出解决问题的各点坐标,若想证明∠ATM=∠AF1T,只需考虑两角的正切值,从而形成解题路径(具体解题过程略).
2. 从多角度观察出发
在解题教学中,教师需引导学生从不同的角度观察,去找寻题目中的关联,并有目的地变换观察角度从而掌握题目的全貌和內在联系. 准确地观察角度可以让学生充分感知题目信息的内在关系,让解题策略水到渠成.
例2:已知函数f(x)= (0≤x≤2π),该函数的值域是( )
A. - ,0 B. [- ,0]
C. [-1,0] D. [- ,0]
分析:若是本题从三角函数的角度着手,考虑y2= ,那么过程的烦琐是必然的. 可以引导学生牢牢把握函数的特征,转化观察和思考的角度,通过构造单位圆,借助斜率知识,则可豁然开朗. 于是y= = .
①当sinx-1≠0时,原式等价于y= . 令k= ,并构造单位圆,从斜率的几何意义得出k∈[0,+∞),所以k2∈(0,+∞), ∈[1,+∞),所以 ∈[-1,0),即y∈[-1,0).
②当sinx-1=0时,即sinx=1时,y=0,
综上所述,值域是[-1,0],故本题选C.
3. 从动态与静态观察相结合展开
在数学中,对于一些较为复杂的命题,学生可以将完整的命题进行分解,从而形成多个小命题,并以动、静结合的方式着手观察,从而打破常规进行分析,进一步得出正确判断,并以变化的思想为指导,分解观察后再进行组合观察,在动、静结合中揭示规律,在深入观察中解决问题,促进学生思维的多向性的形成[2].
例3:已知点P为圆A:x2+(y-2)2= 上的一动点,点Q为椭圆x2+4y2=4上的一动点,请试求出PQ的最大值.
分析:本题所涉问题为两动点之间的最大距离,因此具有较大的难度,学生不易得出头绪. 如果直接设P与Q两个动点,那么思路卡壳是毋庸置疑的. 那么在此处我们是否可以尝试将问题转化为一动点和一定点的问题进行解决呢?深入观察并变通思路,可以思考得出:若要令PQ取到最大值,那么直线PQ则须过圆A的圆心A(0,2),此时则可以顺势将问题转化为求AQ的最大值,这里的定点A自然就变为了求解的主要元素,动点P则可以暂时至于一边,解题思路就此呈现:
设Q(x,y),则有AQ= . 因为x2+4y2=4,所以x2=4-4y2,所以AQ= = = = . 所以当y=- 时,AQ可以取到最大值,最大值为 ,从而得出PQ的最大值是 + .
4. 从学会观察隐含条件出发
学生在解题过程中思路受阻往往都是因为不善于挖掘隐含关系和条件导致的. 因此,在解题教学中,引导学生观察并挖掘隐含条件是解题中不可忽视的重要环节,也是解题关键所在.
例4:已知△ABC中,A,B均为锐角,且有sin2A+sin2B=sinC,请试判断△ABC的形状.
分析:观察题设,可转化为sinA(sinA-cosB)=sinB(cosA-sinB). 观察并分析题中的隐含条件,有sinA>0,sinB>0,cosA>0,cosB>0,且有0~90°时,正弦函数递增,余弦函数递减. 再从条件易知A和B对称,若设B≤A,当A>B>45°或是当B
5. 从类比观察中得以提升
类比观察是学生数学学习中常用的观察方法,是从一般到特殊,从特殊到一般地进行观察. 在解题教学中,教师为了引导学生有目的、有方向地进行观察,并全面精准地把握事物特征,可以对一些命题或题设进行变化,让学生在类比观察中找寻突破口;而对于较为复杂的命题,教师可以用特殊命题的方式,让学生在类比观察中退而求进,揭示其中的规律和本质,进而提升学生的观察能力.
例5:已知等差数列中有am=n,an=m,且m≠n,求am+n和Sm+n.
分析:从题设中不难看出m和n都不是具体数字,那么这里的审题就存在一定难度了. 针对这一问题,教师可以通过设计以下简单的等差数列进行适时点拨“6,5,4,3,2,1,0,-1…”,同时要求学生自选两项进行观察,如a5=2,a2=5,a2+5=a7=0,d= = =-1.
类比本题,学生顿时茅塞顿开,从题设得出d= = =-1. 又因为am=a1+(m-1)×(-1)=n,可得a1=m+n-1,所以am+n=(m+n-1)+(m+n-1)×(-1)=0,Sm+n=(m+n)·(m+n-1)+ ×(-1)= (m+n)(m+n-1).
总之,数学教师有责任和义务帮助学生发展观察能力,解题教学中观察能力的培养不是一蹴而就的,需要教师在日常教学中一以贯之,更需要全面地行动和实施. 数学教学具有数学独有的特征与魅力,这就要求教师需利用好数学内容中丰富的数学思想方法,要通过科学的训练,激发学生潜在的观察爱好,并掌握有效的观察方法,从而形成主动观察和善于观察的习惯,只有这样才能发展他们的数学核心素养,才能更好地解决数学问题[3].
参考文献:
[1] 吴光潮. “模型+题组”,激活学生观察能力——以“三棱锥外接球问题的模型分析和教学题组设计”为例[J]. 中学数学,2018(11).
[2] 何维. 浅析数学教学活动中学生观察能力的指导[J]. 科技信息:科学教研,2008(09).
[3] 常宏燕. 浅谈数學教学中学生观察能力的培养[J]. 中华少年:研究青少年教育,2012(11).
