关注学科融合，培育核心素养

赵海涛

[摘  要] 概念在具体情境中抽象，知识在学科间深度融合，性质在学科内类比，思想在形与数间转化，向量知识使物理和数学、几何与代数完美结合. 因此在向量教学中要交给学生研究问题的方法、拓展学生获得知识的渠道.使学生在思考中发展自主能力、在交流中提升表达能力、在学习中形成数学核心素养.

[关键词] 融合;抽象;类比;运算

课程内容分析

1. 教材分析

向量是近代数学中重要和基本的概念之一，有深刻的几何背景，是解决几何问题的有力工具. 向量是沟通代数、几何与三角函数的一种工具，有着极其丰富的实际背景，在数学和物理学科中具有广泛的应用[1] . 向量既是几何研究的对象，又是代数研究的对象，是课程标准五个必修主题之一“几何与代数”的重点内容，几何与代数是高中数学课程的主线之一. 在必修课程与选择性课程中，突出几何直观与代数运算之间的融合，即通过形与数的结合. 感悟数学知识之间的联系，加强数学整体性的理解[2] . 向量是高中研究三角函数、曲线、平面和空间几何关系的重要工具，也是进一步学习高等数学以及力学、电学等学科的重要工具. 教材第2.1节通过物理实例引入了平面向量的概念，介绍了向量的模、相等向量、单位向量、零向量以及共线向量等基本概念.本节课是继向量基本概念后研究向量运算的第一节课.运算（运算律）是向量的灵魂，加法是向量的第一运算，是最基本、最重要的运算，是学习向量其他运算（减法和数乘）的基础. 在本单元的教学中起着承前启后的作用.

2. 教学目标

根据新课标“以学生发展为本，落实立德树人”的基本理念，以“展现素质教育功能、提升学生数学核心素养”为目标. 本节课的设计将“几何直观与代数运算”“数学与物理”之间完美融合，通过形与数的转换体现数学知识间的联系、强化学科融合;落实学科核心素养，提高学生学习兴趣. 因此把本节课的教学目标确定为：

（1）抽象向量加法的概念、理解向量加法的意义，掌握向量加法的运算和运算律;

（2）体验由物理模型抽象数学概念的过程;

（3）培养数学抽象、逻辑推理、数学运算等核心素养;

（4）认识数学的价值，提高数学兴趣，养成良好的学习方法和习惯.

3. 教学重点与难点

教学重点：向量的加法运算（法则和运算律）.

教学难点：向量加法法则的理解和运用.

学情分析

学生已经掌握物理中的位移和力等矢量知识，了解矢量的合成方法和意义. 矢量是向量的物理模型、具体表现，为学生研究向量加法运算提供了实际背景.

教学过程

1. 共同回顾，导入新课

（1）回顾与分享：向量的基本概念.

（2）问题引入：物理中有哪些与向量相似的物理量？它们能运算吗？

师生一同回顾物理学中位移的合成方法和力的合成方法.

设计意图：本节课重点和难点的突破都需要依靠物理知识来完成，故重点复习物理中的位移和力的知识，为本节课的顺利进行做好铺垫.

2. 类比抽象，形成概念

学生活动1：在坐标纸上完成两个不共线矢量（向量）的合成.

师：矢量抛开它的物理意义，即数学中的向量.在数学中把求两个向量和的运算称作向量的加法，物理中的位移合成和力的合成都可以看作是向量的加法，除去物理意义就是向量加法的“三角形法则”和“平行四边形法则”.大家思考一下这两个法则应用的要点在哪里？

学生1：三角形法则是“首尾相连”，平行四边形法则是“起点相同”.

师：总结得很好，但还能不能再细致一点呢？

学生1：三角形法则重在“首尾相连连首尾”，平行四边形法则重在“起点相同连对角”.

师：非常精炼的总结，既说出了法则的使用要点，也说出了求和结果的形式.那这两种法则对于两个共线向量是否适用呢？

学生活动2：在坐标纸上完成共线向量求和法则的验证，同桌之间交流做法是否适当.

结论：三角形法则对任意两个向量求和都适用，平行四边形法则适用于两个不共线向量求和.

师：我们知道实数中“a+0=a”，那么任意一个向量a与零向量的和是什么呢？

学生齐：任意向量a与零向量的和还是向量a.

设计意图：此环节意在培养学生的数学抽象能力.引导学生利用物理中位移和力的合成，来解决向量的加法运算，并用图形（三角形和平行四边形）准确地描述、用语言高度地概括，突出本节课的重点. 强调数学与生活，以及其他学科的联系，使抽象的数学概念找到可以触碰到的模型，加深学科知识深度融合，使学生养成在日常生活和实践中抽象数学问题的习惯和能力.

3. 合作交流，深化概念

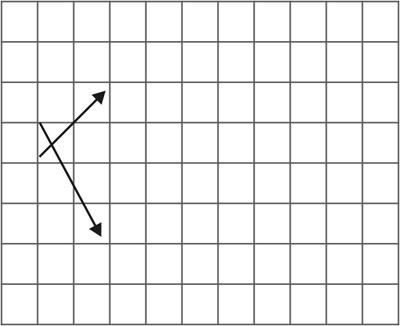
例1：根据图1中所给的向量a，b，做出向量a+b的结果.

图1

学生活动3：在坐标纸上用两种法则完成向量求和，同组同学之间对比、交流作图心得.

师：两种做法结果一致吗？说明什么？

学生2：结果是一样的，说明两种方法本质是一样的.

学生3：任意两个向量的和都是存在的，并且结果是唯一的.

师：这个发现非常好，向量的加法和實数加法一样，结果存在且唯一，这就说明向量的加法是有意义的，解法是多样的.大家还有发现吗？

学生4：通过平行四边形法则我发现“a+b=b+a”，也就是说向量加法满足交换律.

师：你们发现了吗？同意他的说法吗？

学生：同意.

师：实数加法除了交换律还有其他运算律吗？向量也会满足吗？

学生5：实数加法还有结合律，向量加法应该也适用.

师：应该？那就是不确定了，下面大家在坐标纸中试着验证一下向量的加法是否满足结合律“（a+b）+c=a+（b+c）”.

学生活动4：探究“向量加法结合律（a+b）+c=a+（b+c）”.

利用加法法则验证向量结合律，小组内进行交流，学生讲述验证的方法和过程，展现严谨的推理过程.

学生6：（如图2）

（a+b）+c=（ + ）+ = + = ;

a+（b+c）= +（ + ）= + = .

所以（a+b）+c=a+（b+c）成立.

师：推理严谨，证明完美.

设计意图：体会从向量的求和法则（几何图形）中发现问题、提出命题、验证命题的过程;学生类比实数运算法则，猜想向量加法运算的结合律，并利用掌握的加法法则进行探索和论证，有逻辑地表述结论.在探索论证中感悟数学的严谨、在图形的建构中欣赏数学的和谐统一，意在培养和发展学生的推理素养，形成理性思维.

4. 典例训练，强化运算

例2：化简：

（1） + ;

（2） + + ;

（3） + + + .

练习1：如图3所示，O为正六边形ABCDEF的中心，化简下列向量：

（1） + =________;

（2） + =________;

（3） + =________.

练习2：（ + ）+（ + ）+ =________.

设计意图：（1）意在增强学生的运算能力，利用发现和总结出来的正确结论解决数学问题，熟练向量的加法运算过程和运算思路，提升运算能力.

（2）学生通过例2（3）、练习2可加深对三角形法则“首尾相连”的理解. 另外，可创新三角形法则总结出向量加法的多边形法则，便于求n（n≥3）个向量的和.

多边形法则（如图4）： + + +… = .

5.？摇直观感知，深化性质

师：已知力F1=3 N，F2=4 N，那么“两个力的合力”的大小取值范围是什么？

学生7：“两个力的合力”的大小取值范围是大于或等于1 N，小于或等于7 N.

师：看来物理知识掌握得很好哟，那么我们去除物理意义，能否得出a+b的取值范围呢？

学生活动5：探究“a+b的取值范围”.

学生8：类比力的合成效果，我们小组得出a-b≤a+b≤a+b.

师：大家同意他们小组的结论吗？

学生9：我认为不够准确，我们小组的结论是a-b≤a+b≤a+b.

师：大家看到他们两小组结论的差异了吗？你觉得哪个小组更准确、更合理？

学生：同意第二小组的结论，他们更准确地说明了模的取值范围.

师：你们讨论过左右两边的等号何时成立吗？

学生10：我们小组讨论了，结论是当向量a，b方向相同时右边取等号，当向量a，b方向相反时左边取等号，当向量a，b中有一个为零向量时两边同时取等号.

师：你们的结论非常准确和全面，看来你们的合作是非常有效的，还有不同的探究方法吗？

学生11：我们小组利用三角形法则和三角形性质“两边之和大于第三边，两边之差小于第三边”，也得到了相同的结论.

师：很好，大家的思路很开阔，思维很严谨，限于时间关系我们课下可以继续交流不同的探究方向和方法.

设计意图：设置探索性问题意在增强学生的合作交流、直观想象能力，从合力大小或三角形的三边关系中判别、抽象、总结出a+b的取值范围，并对两边等号的取得条件进行探索，充分利用物理模型和几何模型，将图形关系转化为数量关系，在几何图形中抽象数学结论、在具体情境中感悟数量关系，提升建模能力.

6. 总结与提升

学生自主回顾和归纳本节课的内容.

设计意图：让学生静下心来总结本节课收获了哪些知识、方法和思想，有助于培养学生良好的学习习惯，同时保证学生的语言表达能力和概括能力等思维品质得以发展.

回顾与反思

教学的重点是学生的学. 学是中心，会学是目的. 因此，在教学过程中，从教材和学生的实际出发，按照学生认知规律、智能发展、知识水平，充分发挥学生在学习中的主体作用，运用多种教学手段，调动学生学习的主动性和积极性.

本节课重视概念形成及概念深化过程，重视知识的发现和发展过程，重视直观想象和严格的推理过程，有层次地提出问题促进知识的自然延伸，提供给学生独立思考、合作探索、共同研讨的机会.学生通过对这些“有层次”的问题进行探究，对向量加法由感性认识到理性认知，最后建构自己的知识体系.

本节课设计采用“抽象——概括”“探究——交流”的模式，从物理知识入手抽象向量加法的概念和加法法则，并利用几何图形直观表述;类比实数与向量猜想向量的运算性质和运算律;利用合力的范围或是三角形的三边关系得出向量a+b的取值范围等，教给学生“动手做，动脑想;多联想，严求证”的递进式学习方法. 这样做，既增加了学生主动参与的机会，又增强了参与意识，教给学生获取知识的途径和思考问题的方法.使学生真正成为教学的主体.在具体情境中建构新知;在學科融合中感悟数学的简洁、和谐之美;在探究中提升数学兴趣;在研讨、交流中发展自主能力和表达能力;在学习中逐渐形成数学核心素养.

参考文献：

[1]  章建跃. 普通高中课程标准实验教科书数学（必修4） [M]. 北京：人民教育出版社，2018.

[2]  李龙才. 普通高中数学课程标准（2017年版）[M]. 北京：人民教育出版社，2018.