数学核心素养下的大单元结构化教学设计
2020-03-27秦国清

[摘 要] 平面向量作为高中数学的核心概念,集数、形于一身,是数形结合的最好体现,它沟通了代数、几何、三角之间的联系,是高考重点考查内容.文章中笔者根据自己的课堂教学实践来谈平面向量的单元复习,使平面向量复习做到既能梳理巩固已学知识,又能发展数学思维,让学生从中体会研究数学对象的心路历程,领悟用数学的观点看待和认识世界的思想真谛.
[关键词] 平面向量;单元复习课;大单元结构化教学
任何系统都有结构,系统只有开放,与外界有信息交换,才可能使结构有序. 数学教学也不例外.数学概念是反映数学对象本质属性的一种思维形式,是导出数学定理、法则的基礎. 准确领悟核心概念是学生获得系统数学知识的源泉,是学好高中数学的关键. 数学核心概念作为一个本源概念时,当它蕴含着重要的数学思想时,它所涉及的内容将更为广泛,有着不可或缺的指引作用;当它预示着数学方法的重大变革时,主要体现在方法的应用上.具体地说,数学核心概念嵌入在完整的概念体系中,起着核心关键作用,广泛地与其他的概念联系在一起,建构起良好的数学知识结构,形成完整有序的系统. 教学时要厘清数学概念的发展脉络,树立“整体观”和“系统观”.
平面向量作为高中数学的核心概念,与函数、数列、解析几何、立体几何、不等式等知识都有内在联系,是高考重点考查内容. 如何使平面向量复习做到既能梳理巩固已学知识,又能发展数学思维、领悟数学思想,是摆在教师面前的一道难题. 本文笔者就自己的课堂教学实践谈谈平面向量的复习. 笔者以为本节课的复习,重要的不是回顾向量的形式化定义及几个相关概念,而是再次体会获得数学研究对象、认识数学新对象的基本方法,蕴含了用数学的观点刻画和研究现实事物的方法和途径,这是一个带有本源性质的再认识过程.
平面向量单元复习(一)
执教:秦国清
学习目标
理解平面向量中的相关概念;掌握平面向量的基本运算;体会向量研究问题的思想方法.
学习过程
活动一:复习回顾
教者提问向量概念,举实例引入复习.
向量是刻画现实世界的重要数学模型,与实际生活的紧密联系,在解决实际问题中有广泛应用,生活中有向量,生活中用向量. 让学生感受数学的价值,学会用数学的思维方式去观察、分析现实世界,去解决日常生活和其他学科学习中的问题.
1. 已知点D为△ABC边BC的中点,设 =a, =b,则 =________. (用a,b表示)
2. 已知a=(1,0),b=(2,1),若ma-b与a+3b共线,则实数m=________.
3. 已知e1,e2是夹角为 π的两个单位向量,a=e1-2e2,b=ke1+e2,若a⊥b,则k的值为________.
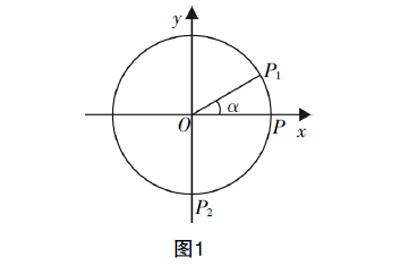
4. 如图1,在平面直角坐标系xOy中,点P1(x1,y1)是单位圆上的一点,P,P2分别是单位圆与x轴正半轴、y轴负半轴的交点,设∠POP1为α. 若α= ,则 · =________.
活动一的实施,为学生课前预习,并小组讨论,形成章节知识框架,课上小组代表展示,其他小组成员补充,教师总结提升完成.
设计意图:活动一设置了4个小题,帮学生复习回顾本章节的基本知识. 在复习回顾过程中要引导学生领悟向量概念的本质特征,类比数的概念获得向量概念的定义及表示,类比数的集合认识向量的集合,类比直线(段)的基本关系认识向量的基本关系.要使学生从中体会到认识一个数学概念的基本,为学生自觉、有序、有效地研究向量问题提供固着点.
第1、2小题在明确向量的概念特征后,着重从向量几何表示和代数表示出发,通过向量的加、减、数乘等线性运算,如利用向量的数乘运算可以刻画平行和伸缩,引出向量共线定理;通过向量的加、减的基底运算引出平面向量基本定理. 通过研究向量运算,可以帮助学生发现运算对象的不断扩展是数学发展的一条重要线索.从数到字母,到向量运算又是一次跳跃.从而加深和拓展了学生对数学运算的理解,有助于学生发展运算能力和推理能力,让其体会到数学运算在建构数学系统中的作用.
第3、4小题通过研究向量数量积运算的两种方式(基底和坐标),进一步强调向量有方向,可以刻画角度、直线、平面等几何对象及它们的位置关系;向量有长度,可以刻画长度、面积、体积等几何度量问题运算及其规律.而向量的数量积运算可以刻画垂直、角度、距离、三角函数等.当然长度、角度等度量问题只有有向线段是不够的,必须通过向量坐标化的代数运算,使相关的运算化归为实数的运算,特别指出的是,平面向量基本定理转化为直线坐标系、平面直角坐标系、空间直角坐标系的基本定理,它们实即解析几何发明的本源之一. 至此,向量作为数形转化桥梁的核心作用跃然纸上.数形结合不但是探究数学的思想,解决数学问题的方法,其实也是数学命题的一种根据和来源,更应是探索创新的思维方式.
另外,第4小题的选择着重于向量的应用研究,形式上题目的选取后面有三角形、四边形,选择一个圆作为背景,选题更全面.更主要的是向量的应用为解决三角形问题(平面问题)提供新的视角.教材在安排必修4的内容,非常巧妙精致,三个章节之间存在紧密的联系,向量位于本模块中间章节,充分体现向量双重特性,同时为利用向量数量积推导出三角恒等变换核心(知识的起点)——两角差的余弦公式奠定基础,其中向量运算中的“算两次”的思想方法得以体现.
知识梳理
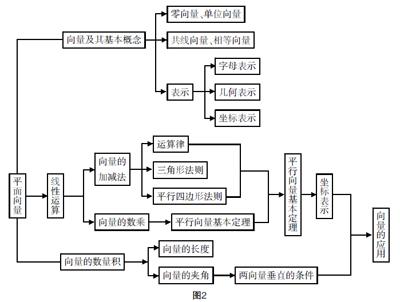
如图2所示:
设计意图:知识梳理时可以从三个方面展开,一是向量概念的本质特征(大小和方向)引发后面的运算以及应用的方式、方法,上面已谈到. 二是从整体的角度,研究与向量密切联系数学概念,它们通常都是以一定的数学思想或方法联系在一起的,如三角函数与向量的交汇,促成了向量、坐标、复数三位一体,使相关的运算化归为实数的运算;明晰了长度与角度的转化联系,促成了极坐标与直角坐标的互化;使直线斜率(倾斜角)等解析几何问题的研究更趋于本质化. 三是从学生获得研究数学新对象的基本方法入手,通过类比的方法, 引导学生找到用数学的观点刻画和研究现实事物的方法和途径,突出了数学学科教学的根本价值——学科育人.
活动二:典型例题
例1:如图3,在矩形ABCD中,已知AB=3,AD=2,且 = , = ,求 · 的值.
(可在例1的基础上,即时变角,把直角变为其他特殊角,再让学生研究)
变式1:如图4,在平行四边形ABCD中,已知AB=8,AD=5, =3 , · =2,求 · 的值.
设计意图:变式1和例1在形式上都是基本几何图形,从小题1的三角形,到例题的矩形,再到变式中的平行四边形,把角的条件、边的条件逐步换掉后,在陌生背景下再來训练学生,本质上都是研究向量数量积的两种基本方法,力求让高一的学生能够牢固掌握.这也符合高考命题的要求,重要的知识反复考.在这里教者要赋予学生更多地参与学习的机会和权利,让每一个学生在自主独立思考的基础上,鼓励学生多思善问,让学生在鼓励中不断调整思维方向. 要给他们充分的时间和机会表达、反思,辨析和体会,让学生养成自动矫正、调节自己的学习行为的能力.使学生的学习始终处于一种有准备的状态,更容易进入“自主学习”的境界.培养自觉、自主、自立的学习者,为学生的终身学习打下坚实的基础.
例2:在△ABC中,∠C=60°,AC=1,BC=2,2 = ,求CE的长.
设计意图:笔者认为,本题能完美地展示解决向量问题的各种方法,但对于高一学生来讲,主要还是从几何和代数的视角,紧紧抓住基底法和坐标法,夯实基础. 教者要站在学生的立场,贴近学生的思维发展区,剖析反映数学知识,演化逻辑的知识序、反映学生学习心理活动的思维序、反映教学流程时空推进的教学序,在“三序合一”中化知为识、化识为能、化能为慧.
变式2:在△ABC中,∠C=60°,AC=1,BC=2,2 = ,D是BC的中点,AD与CE交于点O. 求 .
拓展:如图5,在△ABC中,D是BC的中点,E在边AB上,BE=2EA,AD与CE交于点O. 若 · =6 · ,求 的值.
设计意图:变式2、拓展和例2的解决,从复习回顾的第1小题起就埋下了伏笔,从三角形的中线到三等分点,再到中线的交点——重心,再到变式和拓展,一以贯之的是解决问题的思想和方法,利用向量的加法、减法运算和基底思想很快解决问题,当然也可以利用平面几何的知识解决.
需要强调的是,作为章节复习课,选题必须典型,本节课的选题都是来自课本和高考卷,也有适当的变化.这样解题的入口宽,跟高速公路一样四通八达. 所以变式2、拓展毫无疑问也可以建立坐标系,代数化运算,另外变式2是拓展的特例,拓展是变式2的一般情况. 在向量问题解决方法中特殊化、坐标化也是很常见的.
最后要说明的是,教者要根据课堂的节奏把控教学进度和内容,不要图“高、大、全”,拓展训练来不及可以在后面再探讨. 由于是章节复习的第一课时,我们在梳理完知识框架和发展脉络后,典型例题的研究主要选择求解向量的模长和数量积,下一堂课将在本堂课的完成基础上,解决一些角的问题,以进一步完善章节复习体系.
活动三:课堂小结
设计意图:通过师生共同的复习回顾,让学生进一步感受到:向量是代数的对象,向量是几何的对象,向量是沟通代数与几何的一座天然桥梁,是重要的数学模型,有着广泛的应用.教者要梳理课堂教学发展的脉络,发掘真实的、灵动的、丰富多彩的高中数学课堂,让学生从中体验数学家研究数学对象的心路历程,领悟数学家用数学的观点看待和认识世界的思想真谛.教师要挖掘数学及数学教学的价值,让学生在掌握基本的数学知识技能和思想方法的同时,学会生存、生活和适应社会发展的智慧.
南通教科院曾荣教授认为,本堂课成功地完成了单元复习课的两项目标:知识梳理结构化和例题应用综合化. 既明晰了核心概念的来龙去脉、生长生成,让学生通透知识;又以“合理的选择、适度的变化和充分的活动”让例题教学变得精致而深刻.更重要的教者能挖掘所蕴含的数学思想方法,让学生学习时逐步加深理解,生发出研究数学对象,解决数学问题的方法策略.
对于本节课的“活动单”设计,笔者四易其稿,精益求精. 在随后的课堂教学中顺利达成预期目标,设计意图很好的得以实施. 教学中笔者还发现,两组例题、变式教学时类比、比较、循序渐进进行,效果更佳,更能让学生形成研究向量问题的方法和路径.
必须强调的是,课堂设计和教学要建立在对课程标准、教学内容和教材有深刻理解,对学生的认知水平有较好的把握上,使得知识内容序与学生的学情认知序结合形成有效的教学序;同时以大概念或大观念统领教学的各要素,形成主体协同、要素关联、学力生长、素养聚焦、系统优化的教学结构,建构层级化、关联性的课堂教学系统. 这就是笔者所在学校正在开展的“大单元结构化教学”模式.
教学中教者要合理设问、适时点拨、直达思维的关键处;让学生经历过程、突破难点、直击矛盾的冲突处;要重视思维的自然流露,体现数学的本质特征,关注思维的过程与方式,让数学思维“看得见、听得见”;要站在系统的高度,提炼思想,升华观点. 这样学生将来不管从事什么工作,当面对工作、生活中的困难时,即使忘掉了所学的数学知识,仍然可以从数学的角度,通过深深铭刻在头脑中的数学精神、数学思想方法迅速抓住关键点,有条理地观察、分析、论证,随时随地解决问题. 笔者认为,这才是我们要的数学核心素养,才是学科育人.
