Matlab模拟我国对外投资模式——基于出口冲击的分析

一、前言

近年来，我国“一带一路”倡议提出后，对外直接投资（OFDI）迅速增长。2015年，我国对外投资出现历史性的突破，首次成为全球第二大OFDI经济主体，对外投资流量达到1.47万4美元，占全球对外投资总额的比重提升到9.9%。我国的OFDI快速增长并成为全球最大潜在FDI来源之一，这不由让人联想到日美二战后OFDI的快速增长。日本早期在进行海外投资时，以资源寻求为目的把国内不具有比较优势的产业转移到国外，并把获得的资源支持国内产业，促进了出口。而美国早期是以寻求全球市场整合，把比较优势产业延伸到其它发达国家，结果美国出口减少了。与日美早期OFDI的快速增长一样，中国在2000年后OFDI快速增长。中国OFDI是否表现出像日本一样的出口增强型还是像美国一样的出口替代型呢。由此，本文探讨如何利用Matlab工具对OFDI的出口效应进行模拟。

二、实证分析

目前对经济冲击分析的方法大多数采用向量自回归模型（Vector Autoregressive Models，VAR）进行的。本文实证分析方面运用VAR模型来定量研究经济冲击对我国出口的动态影响。

（一）实证模型

为了对中日美OFDI相同发展阶段的贸易效应进行横向对比，但鉴于传统静态计量分析方法OFDI与出口之间所揭示的关系的局限性,本文采用Sims（1980）提出的向量自回归（VAR）的方法来建模。建立如下的VAR模型：

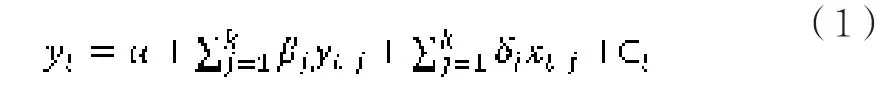
其中，yt是第t期的出口，xt是第t期OFDI，α，γ，βj是待估的系数矩阵，是随机扰动向量，k为滞后阶数。选取的变量分别有中日美三国的出口和OFDI流量。由于数据的限制和可操作性，所有变量均采用1970年至2015年度数据。OFDI数据由UNCTAD数据库提供,出口数据由WTO提供，GDP平减指数由世界银行数据库提供。OFDI和出口均为当期美元，利用GDP平减指数进行通货膨胀调整，最后取对数。

（二）Matlab对VAR模型的模拟步骤

1.本小节叙述如何利用Matlab对VAR模型进行模拟。第一步准备好数据，利用命令 load mydata 对数据进行加载,数据的每一列是一个变量，每一行是一个观测值。数据不能有缺失值。第二步是定义VAR的滞后阶数，如果滞后阶数为3，那么 nlags = 3。如果模型包含常数项，即 hasconst = 1，否则为0。第三步对VAR模型进行估计：

[betaz,sigma,residuals]=estimatevar(data,nlags,hasconst);

估计的结果返回三个参数，第一个参数betaz是VAR的估计系数，第二个参数sigma是协方差矩阵，第三个参数是模型的残差。第四步

2.计算模型的脉冲函数，首先利用协方差矩阵计算结构矩阵 a0rec=inv(chol(sigma)')。其次，利用下面的命令计算脉冲响应：

impzmat =mkimprep(betaz,a0rec,nlags,errshk,nstep);

其中：errshk 指出了哪一误差项接受冲击；nstep 指出了计算多少期的脉冲响应。再次，计算脉冲响应的置信区间：

[cilb,ciub,cilvarb,ciuvarb,varb]=mkimpci(betaz,a0rec,nlags,er rshk,nstep,ndraws,nobs,pctg,residuals);

其中，ndraws 定义构造置信区间的仿真次数；nobs 定义了每次仿真的时间序列有多少观察值，因为置信区间的计算是基于Monte Carlo的；pctg 是构造置信区间的值。

3.脉冲响应画成图行。cilvarb 和 ciuvarb 是计算得到的脉冲置信区间，impzmat是计算得到的脉冲。我们利用这三个数据，用matlab的plot画图，命令如下：

plot([ 100*cilvarb(：,i) 100*ciuvarb(：,i) 100*impzmat(：,i)]);

其中，i表示第i个变量的脉冲响应。

（三）数据平稳性检验与模型的滞后阶数确定

由于大多数时间序列经济数据存在非平稳性问题,可能出现伪回归,本文采用Dickey-Fuller (ADF) 方法进行平稳性检验。利用Matlab对所有变量进行ADF检验。中日的OFDI和出口数据的水平值都是不平稳的，但经过一阶差分后都是平稳的。美国的数据则在水平值已经平稳了。

对于VAR模型,在建立过程中首先要确定模型的最合适滞后阶数k。采用LR统计（序惯检验法）、SC信息准则、AIC信息准则、FPE(最终预测误差)与HQ (Hannan-Quinn)综合判断滞后阶。从表1选准则的计算结果综合考虑,并结自由度的要求,我们确定模型滞后阶数为1。

表1 VAR模型不同滞后阶数下选择准则的取值情况

在确定滞后阶数后，进一步判断其是否满足VAR模型的稳定性条件。 由Matlab计算结果可以判断被估VAR模型的特征方程所有的根的倒数都小于1（位于单位圆内）, 即模型是稳定的。所以k=1最终被确认为模型的最优滞后期。

（四）脉冲响应函数分析

本文利用脉冲响应函数在VAR模型中衡量来自随机扰动项一个标准差的冲击，对出口当前和未来取值动态影响的轨迹。现分别给三个国家的出口一个单位大小的正向冲击，得到出口响应结果如图1所示。从图1-a中可以看出,在期初给日本OFDI一个标准差的冲击后,出口开始下降，下降到第2期的-2.7%。此后开始上升，到第3期由负转为正的，OFDI开始带动出口提升。过了第4期的最高点0.3%，OFDI的出口增强效应开始减弱。图1-b为美国出口的反应情况，当美国OFDI受一个标准差的冲击后，出口从第2期开始上升，上升到第4期最高值4.6%，随后开始下降，但下降的速度较缓慢，OFDI对出口的拉动作用很明显。图1-c描述的是中国的情况，从图中可以看到，当OFDI受到一个标准差冲击后，出口从期初开始上升，上升到第2期就达到最高点1.4%，之后下降较快速，到了第9期OFDI对出口的拉动作用基本消失。

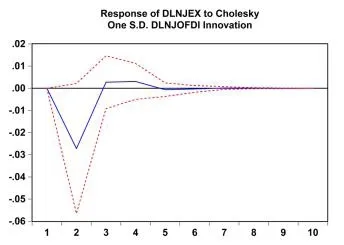
图1-a 日本出口脉冲响应

图1-b 美国出口的脉冲响应

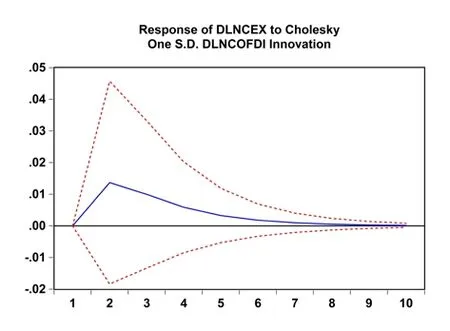
图1-c 中国出口的脉冲响应

从脉冲响应分析可以看出,中日美在OFDI产生冲击的情况下，出口均出现不同程度地向上拉动。美国OFDI的出口增强效应尤为明显，中国的效应不持久，日本的效应则是先下降后上升。日本在进行边际产业革命时，先将国内已丧失比较优势的产业转移到国外，在这个过程中不可避免地减少了日本的出口。这些产业到了东道国后，重新获得比较优势，并获取海外的能源以支持国内产业，最后促进日本的出口。所以日本的OFDI是的出口效应是先下降后反弹。与日本OFDI的出口增强模式相比，美国则呈现不同的模式。美国是具有垄断优势的企业进行OFDI，这些企业技术优势突出，从而更容易借助OFDI扩大出口。

中国的情况与美国类似，随着OFDI的增长，出口呈现增强模式。主要原因有：中国通过OFDI在海外寻求国内稀缺的资源以及维护原料来源的稳定性，确定国内产业的稳健性，提高出口；中国通过OFDI，吸收学习国际管理经验、获取国际先进技术，并引进中国再进行本土化，提高自己产品的竞争力,然后推向市场,促进出口；中国通过OFDI在海外抢占市场，解决国内市场饱和、生产过剩等问题，为了寻求生存之路，通过OFDI将产品转出到国外，拉动了出口。但由于中国未能在海外获得核心技术，OFDI的出口增强效应不具有持久性。总之，相比日本模式，中国OFDI的出口效应遵循着美国模式。

三、结论

本文通过建构VAR模型分析中日美三国在1970年至2015年间OFDI对出口的效应。由脉冲响应函数分析发现,日本OFDI对出口的作用是先抑制后促进，而中美OFDI从期初开始就对出口有拉动作用。也就是说面对OFDI的正向冲击时，日本出口是先收缩后反弹，而中美两国的出口都呈增强型。在这三个国家中，美国OFDI对出口促进表现出较长的效应，中日的促进作用不具有持久性。