Maxwell分布参数的最短置信区间研究
2021-12-07吴志超程义斌郭宝才
吴志超,程义斌,孙 波,郭宝才
(1. 浙江工商大学统计与数学学院,浙江 杭州 310018; 2. 中国疾病预防控制中心环境与健康相关产品安全所,北京100021)
0 引言
总体参数的区间估计是统计推断的一个重要内容,已广泛应用于经济与生产实践.衡量置信区间的优良性有两个标准:置信水平和区间长度.给定置信水平,区间长度越短,参数估计精度就越高.传统的区间估计是按概率对称方法来选取的,即等尾置信区间.但对于偏态总体或偏态抽样分布而言,等尾置信区间长度显然不是最短的.有许多学者针对最短置信区间问题进行了相关研究.如文献[1-3]对正态总体方差的最短置信区间进行了比较详细的讨论.王秀丽[4]介绍了均匀分布区间长度的最短置信区间.徐美萍等[5]对Weibull分布中尺度参数的最短置信区间问题进行了研究.李广正[6]讨论了两正态总体方差比的最短置信区间问题.李云飞等[7]利用样本分位数来构造枢轴量,给出了双参数指数分布的等尾置信区间.
Maxwell分布是可靠性统计和实践中常见的寿命分布之一,制造行业、立式镗床的使用寿命等均遵循该偏态分布,在统计动力学中也有诸多应用.国内学者对这一问题的研究比较少.桂春燕[8]给出了Maxwell分布的一些特性,但没有讨论参数估计的问题.王晓红等[9]在文献[8]的基础上给出了Maxwell分布参数的极大似然估计和Bayes估计.文献[10-13]构建了统计质量控制图监控Maxwell分布尺度参数的变化.
就笔者所知,还没有文献讨论Maxwell分布参数的最短置信区间问题.本文将构建枢轴量来计算Maxwell分布尺度参数的最短置信区间,并与传统的等尾置信区间进行比较.最后用一个实例进行分析和说明.
1 Maxwell分布与枢轴量
若随机变量X的概率密度函数为
则称X服从参数为σ的Maxwell分布,记作X~Maxwell(σ).
引理1设X1,X2,…,Xn为来自总体X的简单随机样本,那么σ2的极大似然估计为

(1)
引理2设总体X~Maxwell(σ),那么X2/2σ2服从形状参数为3/2、尺度参数为1的伽马分布,即X2/2σ2~Gamma(3/2,1).
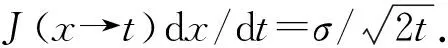
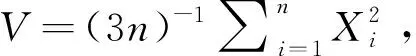
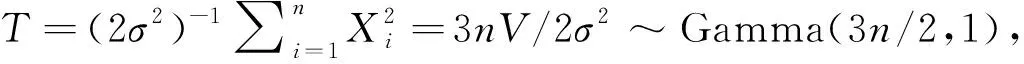
(2)
即T的概率密度函数为

(3)
本文将T用作枢轴量来求解σ2的置信区间.
2 等尾与最短置信区间
设X1,X2,…,Xn为来自总体X~Maxwell(σ)的样本,若统计量L(X1,X2,…,Xn)和U(X1,X2,…,Xn)满足
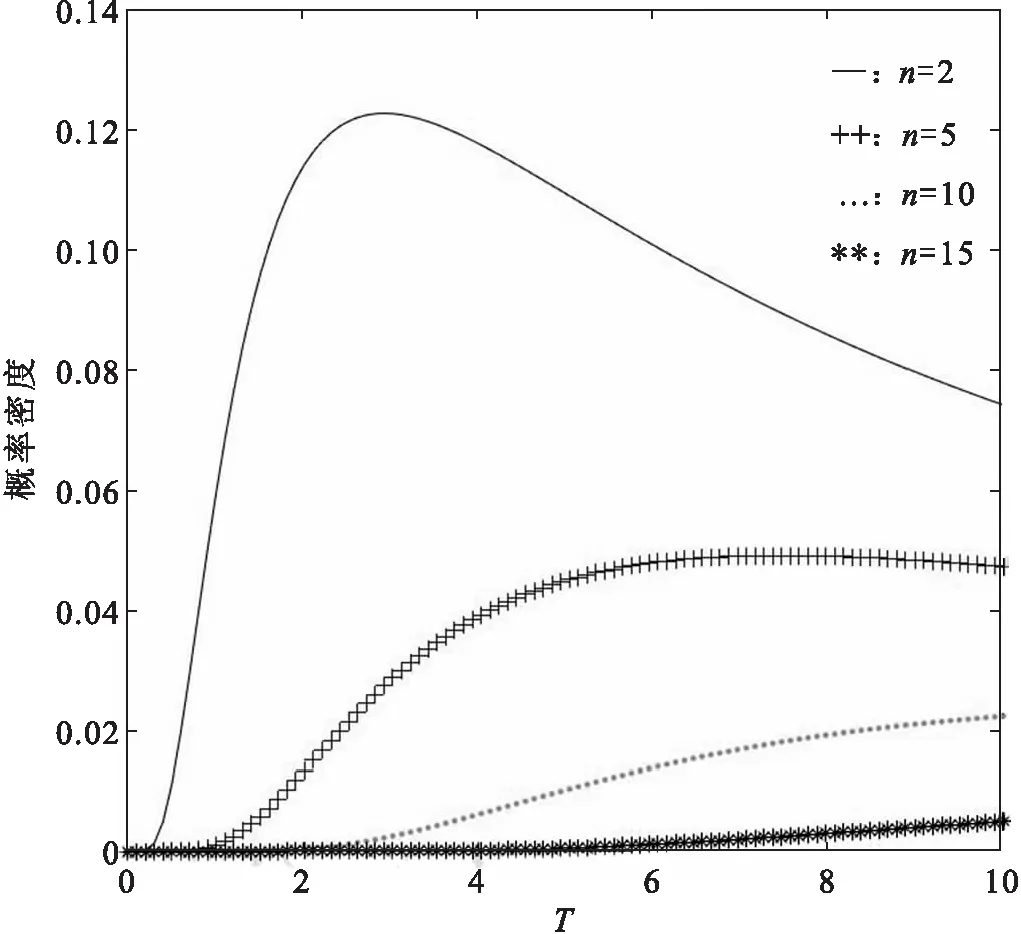
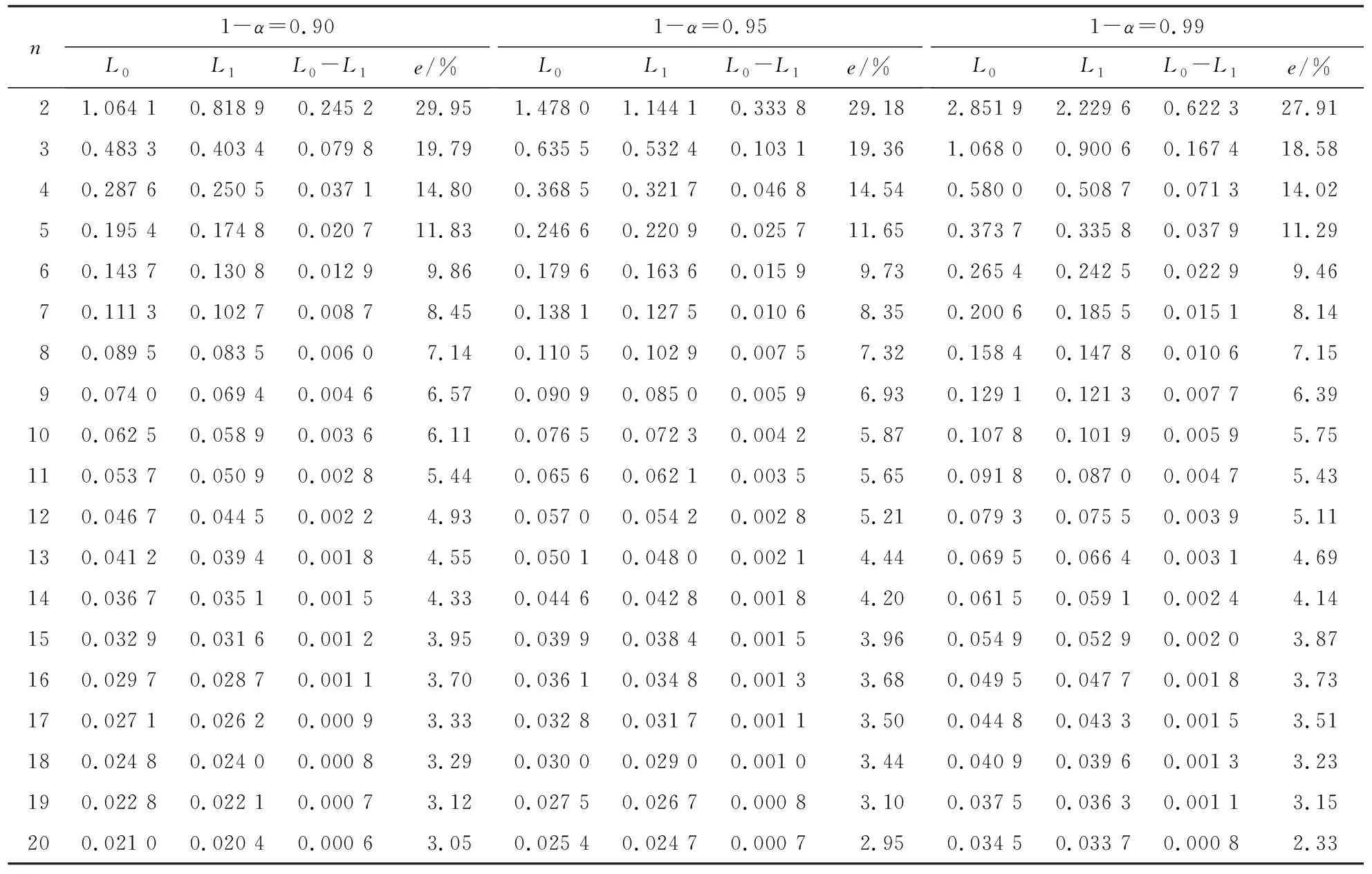
P(L<σ2 (4) 则称(L,U)为σ2的置信水平为1-α的置信区间.因为 所以式(4)等价于 (5) (6) 由于枢轴量T的分布并不对称,因此σ2的等尾置信区间长度不是最短的,从而精度也不是最高的.图1表示在不同的n下枢轴量T的图像. 图1 不同样本容量下枢轴量T的概率密度曲线Fig.1 Probability density curves of T under different values of n (7) 定理1设总体X服从Maxwell(σ),X1,X2,…,Xn为来自该总体的样本,条件极值问题(7)中的a,b应满足下列方程: (8) 证明利用拉格朗日数乘法,令 H(a,b,λ)=1/a-1/b+λ[FT(b)-FT(a)-1+α], 对a,b分别求偏导数并令其为0,有 于是 a2fT(a)=b2fT(b)=-1/λ. (9) 将枢轴量T的概率密度函数fT(t)代入式(9),化简得a1+3n/2e-a=b1+3n/2e-b,因此结论成立. 定理2Maxwell分布参数的最短置信区间存在. 令g′(w)=0,则有 其中w0=1+3n/2.即g(w)为单峰函数,当0 因为 由中值定理知:必存在a=a*(0 定理3Maxwell分布参数的最短置信区间是唯一的. 因为 a*2fT(a*)=b*2fT(b*)=-1/λ*>0,a*<3n/2+1 所以 同理, 由于式(8)的复杂性,方程组没有分析解.本文利用MATLAB来求方程组的数值解,样本容量为n∈{2,3,…,20},结果如表1所示. 表1 σ2最短置信区间的精度分析Tab.1 The accuracy analysis of the shortest confidence interval for σ2 由表1可观察到,在同一置信水平下,最短置信区间的精度一致优于传统的等尾置信区间,特别是在小样本情况下,提升效果更显著.随着样本容量的增大,两者的差异性越来越小. 采用的实际数据来源于文献[13].选取32个垂直钻孔机数据,立式镗床的故障时间(h)如下:2 802,2 937,2 136,4 359,4 020,1 781,2 816,2 655,3 886,2 296,3 158,3 695,4 155,3 811,2 380,376,2 172,3 705,2 848,4 339,2 076,2 672,3 632,1 976,1 700,1 596,1 701,3 575,3 802,4 351,4 291,808. 文献[13]已证明Maxwell分布最适合此数据. 两者的绝对误差为44 441.3,相对误差为2.45%.最短置信区间明显小于等尾置信区间,说明最短置信区间的精度更高.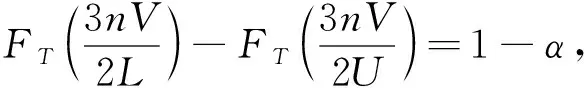
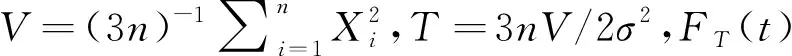
2.1 等尾置信区间
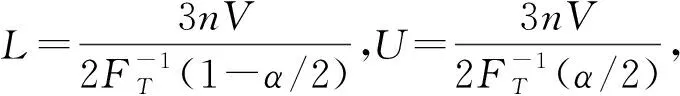

2.2 最短置信区间
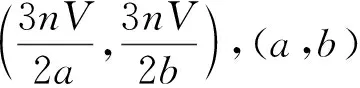
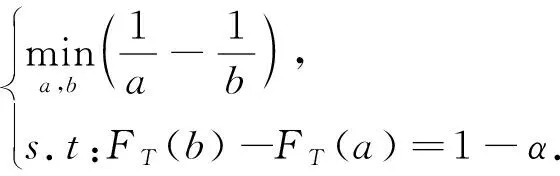
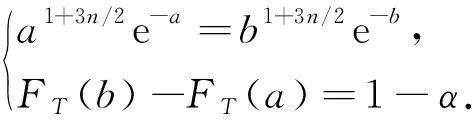
3 最短置信区间存在性和唯一性证明
3.1 最短置信区间的存在性证明
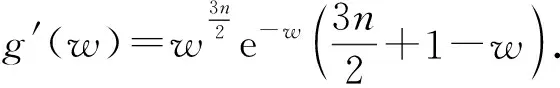
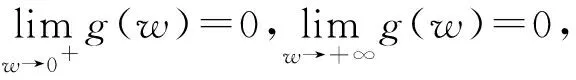
3.2 最短置信区间的唯一性证明
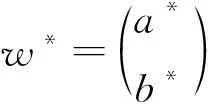
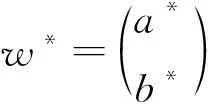
4 计算结果与实例分析
4.1 计算结果
4.2 实例分析