车险数字化变革

◆李思佳

一、问题的陈述

（一）问题背景。近年来，车险在我国保险行业中所占比重最大，投保率也在不断提高。我国目前的车险定价主要与车自身的情况（车型、车的购置价、座位数、排量、购车年限等）有关，因此车型相似，车险保费也差不多。

我们预见未来车险的定价将主要取决于驾驶人自身的情况（驾驶行为、年龄、职业、家庭状况等），因此车险保费将不再单调。

我们可以运用数字化技术建立客户精准画像，来制定不同的营销方案。

（二）问题提出。针对客户信息建立能够刻画每一位客户续保率的数学模型。

二、模型假设

（一）模型假设。为了使得问题更易于理解，我们作出以下合理假设：

▪ 每种品牌的车辆的出险率是稳定不变的。

▪ 假设已投保立案后必有已决赔款。

▪ 假设附件数据为同一个保险公司。

▪假设投保类型为“单商业”时,其交强险已在其他公司缴纳。

三、模型的建立与求解

（一）数据预处理。题目提供了1个附件，附件中的数据给出了客户车险的相关信息，对于众多的客户信息数据，我们使用EXCEL对数据做了以下预处理：

清理数据，剔除数据坏点：

①客户类型为个人的时候，被保险人性别却是NA等类似其他错误；②三者未投保后面三者险保额却有金额等类似其他错误；③前面保单性质为转保后面是否续保却写的是等类似其他错误；

利用以上数据，对问题进行求解分析。

（二）模型建立与求解

1.模型的选取。一般来说，实际问题中影响因变量的因素可能很多，从应用的角度既希望将所有对因变量影响显著的自变量都纳入回归模型，又希望最终的模型尽可能简单，既不包含那些对因变量影响不显著的自变量，这就是所谓“变量选择”。逐步回归是一种迭代式的变量选择方法，通过逐步回归来选择变量，建立多元线性回归模型。

续保概率逐步回归程序的最终输出图形如下图所示：

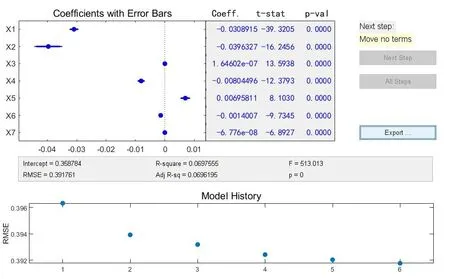
图1 MATLAB逐步回归程序运行的最终输出图形

通过图1右侧的Export菜单可以传送输出数据，得到的结果如下表所示：

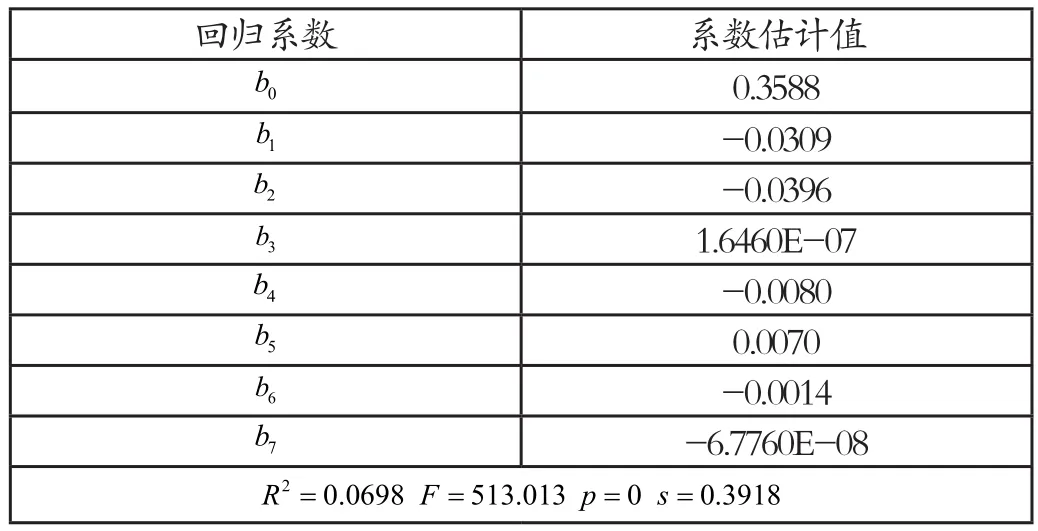
表1 逐步回归的最终结果（=47898）

最终模型为：