确定有限级数解的阶数上界的一种n阶展开方法
2021-06-03宋宸苇柳银萍
宋宸苇, 柳银萍
(1. 华东师范大学 计算机科学与技术学院, 上海 200062; 2. 华东师范大学 数学科学学院, 上海 200241)
0 引 言
齐次平衡方法是构造非线性演化方程精确解的一种有效方法, 其中假设变换的阶数是通过部分地平衡最高阶项来确定的[1-7], 这就是所谓的齐次平衡原则. 下面以双曲正切方法[8-13]为例, 简要介绍齐次平衡原则.
考虑如下非线性演化方程

1 扩展的齐次平衡原则
在这一章中, 我们仍以双曲正切方法为例来介绍扩展的齐次平衡原则的基本思想和步骤.
考虑非线性演化方程

其中u=u(x1,···,xn,t) .u(k)表示u的所有k阶导数的集合, 比如u(1)={ut,ux1,···,uxn}. 假设
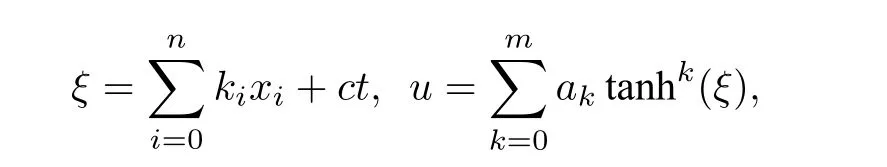
将它们依次代入原方程, 得到了一个关于 t anh(ξ) 的多项式方程, 这个多项式的阶数列表为

基于已有的齐次平衡原则可建立如下阶数方程
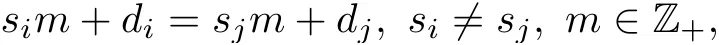
来确定阶数m的值, 即忽略了si=sj的情况. 但是, 我们不能否定平衡这些情况的可能性, 因此, 本文将平衡条件重新定义为
• 整数性约束:m∈Z+;
• 平衡性约束:∃i̸=j,sim+di=sjm+dj;
• 最大性约束:∀k̸∈{i,j},sim+di≥skm+dk.
令
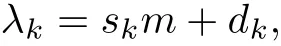
平衡点分类示意图如图1所示. 从图1中可以看出, 有三类平衡点.
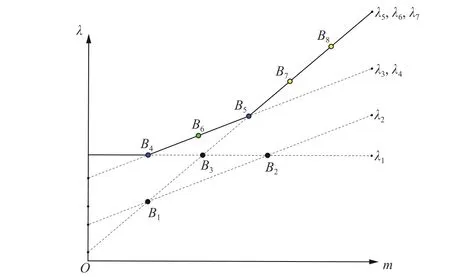
图 1 平衡点分类示意图Fig. 1 Schematic diagram for the classification of balance points
•B1,B2,B3不满足最大性约束, 它们不是平衡点.
•B4,B5可以由平衡性约束唯一确定, 它们是第一类平衡点.
•B6不能由平衡性约束唯一确定, 但可以由最大性约束确定, 它是第二类平衡点.
•B7,B8及它们右侧的一系列整数点满足上述三个平衡条件, 但我们不能确定它们的上界, 它们是第三类平衡点.
本文提出了一种基于第三类平衡点来确定解的阶数的n阶展开法.
2 n阶展开方法
我们注意到, 由于求导的缘故, 阶数m不仅会出现在指数中, 还会出现在一些系数中. 通过考虑第一类和第二类平衡点, 我们可以确定阶数m的上界. 通过考虑第三类平衡点, 即考虑最高n项的指数和系数, 可能会获得阶数m的新的上界. 本文提出的n阶展开方法的思路和步骤如下.
定义一个关于x的m次多项式的n阶展开形式

其中
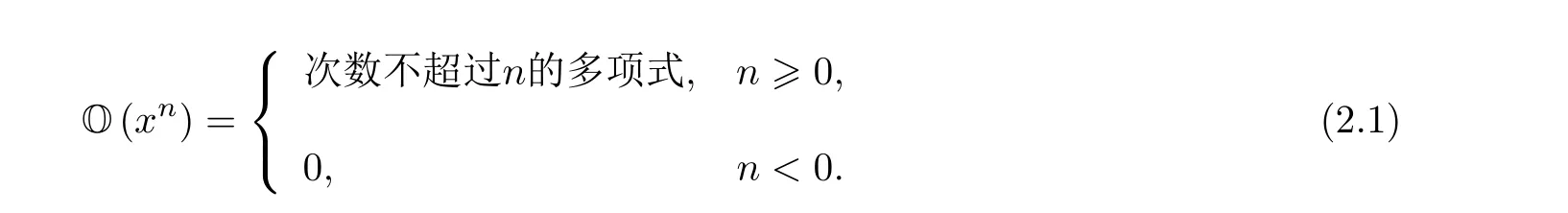
在双曲正切方法中, 令
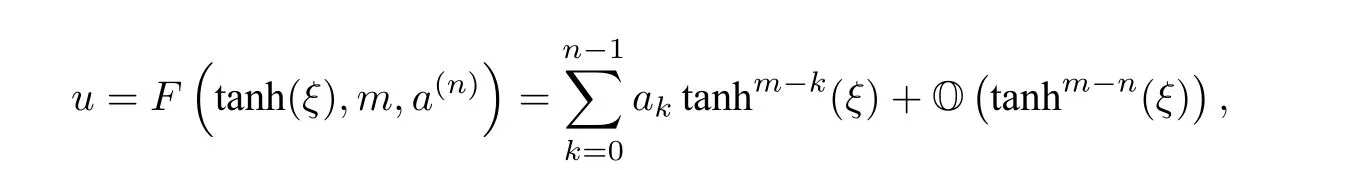
将它代入原方程, 得到的方程通常为关于 t anh(ξ) 的多项式方程. 我们考虑最高的n项, 即n阶展开多项式. 下面定义了n阶展开多项式的乘法、求导和加法规则.
n阶展开多项式的乘法:

我们得到

值得注意的是, 虽然该方程的三类平衡点都存在, 但由于m的最终上界等于由第一类平衡点确定的上界, 因此没有获得新的解.
3 应用实例
在这一章中, 我们将扩展的齐次平衡原则和n阶展开方法应用于几个具体的非线性演化方程, 由此获得了一些新的解.
例 1 考虑(1+1)维非线性演化方程[22]

根据第一类平衡点, 我们有 2m+3=3m+1 , 得到m=2 . 由于有两个相等的阶数 2m+3 , 根据第二类平衡点, 我们有 2m+3>3m+1 , 从而得到m<2 . 在这种情况下, 我们得到m的上界为m=1 . 该方程没有第三类平衡点. 因此, 解的阶数的最终上界为m=2 . 在此基础上, 我们获得了该方程的如下7个解:

4 结 论
本文进一步扩展了原有的齐次平衡原则, 考虑了更多的平衡可能性, 并提出了一种n阶展开方法来确定解的新的阶数上界. 将其应用到双曲正切方法中, 通过三个具体实例可以看出, 基于n阶展开方法确实可以获得所求级数解的新的更高阶数, 并由此获得了所考虑的非线性演化方程的一些新解.需要说明的是, 扩展的齐次平衡原则虽然具有普适性, 但第二类平衡点和第三类平衡点都是基于重复的阶数, 即只有当非线性演化方程的阶数列表中有重复的阶数时, 才能使用扩展的齐次平衡原则, 以此来获得新的更高阶数以及非线性演化方程更多的新解. 另外, 目前关于有限级数解的成果不限于行波解, 还可构造出更一般的有限级数解, 如CRE (Consistent Riccati Expansion)方法, 通过将行波变量替换为关于自变量的更一般的函数, 从而可构造出更复杂的有限级数解, 特别是不同波之间的相互作用解.
