用于能谱本底处理的阶数自适应型正交多项式模型法
2021-07-21杨万里
杨万里,刘 冲,胡 锐
(1.南华大学 电气工程学院,湖南 衡阳 421001;2.中广核久源(成都)科技有限公司,四川 成都 610059)
0 引 言
在能谱数据处理中一个重要的数据源处理过程是从复杂谱中扣除本底,本底扣除的准确性及稳定性直接影响净峰面积计算的精确度。一个效果良好的本底扣除法[1],对于低本底上的强峰、高本底上的弱峰、不同曲率本底上的峰等不同情况,处理后都能获得准确可靠的净峰面积。除此之外,还要求尽可能减少需要用户自己设置的参数,目的是方便大量的谱数据处理[2]。本底处理方法分为两种思路[3-4]:本底估计(先扣除本底再计算净峰面积)和本底模型(用数学函数描述本底,再计算净峰面积时同时扣除)。本底估计包括:SNIP算法(scale normalization for image pyramids,SNIP)[5-7]、傅里叶变换法[8-9]、正交多项式拟合法[10]等。这类方法应用的谱区间宽甚至全谱范围、计算比较简单、速度快,但精度不高、参数较多且设置麻烦。本底模型包括:线性多项式模型[11]、正交多项式模型[3]等不同函数描述本底。它们根据高斯函数或改进型高斯函数描述特征峰,采用最小二乘拟合法同时确定本底函数、特征峰函数的相关参数,即可求出净峰面积。这类方法本底处理结果比较准确,但谱区间较窄、计算复杂、速度不快、需要用户根据谱形特点选择本底函数及多项式函数的阶数。本文介绍的阶数自适应型正交多项式模型法可以有效地将本底估计法和本底模型法结合起来,充分利用谱数据,建立起更加完善的数学模型。
1 算法理论分析
J.B.Olsen[10]提出用一系列正交多项式的线性组合拟合能谱,以迭代方式调整拟合权重(权重主要用于区分峰区和本底区),逐渐“剥除”谱峰,最终拟合曲线中只包含本底。由于采用正交多项式拟合,计算过程大大简化,且数值上更加稳定,阶数可以达到30,可用于本底曲率较大、复杂本底、拟合区间宽等情况。正交多项式的阶数可由用户设定。该方法的主要公式见式(1)~式(6)。
(1)
(2)
(3)
(4)
p0(i)=1p1(i)=i-α0
pj(i)=(i-αj-1)·pj-1(i)-βj-1·pj-2(i)
(5)
(6)
其中:i—道址,从1~N;
j—阶数,从0~n;
bi—道址为i时的背景;
cj—合成谱阶数为j时的系数;
r—自适应参数;
pj(i)—道址为i时合成谱的阶数;
yi—道址为i时的能谱;
wi—道址为i时的权重背景;
αj,βj和γj都是常数。
B.Vekemans等[3]提出用高斯函数表示能谱的特征峰,本底用正交多项式的线性组合函数表示,那么式(10)就可以表示能谱谱线。先用正交多项式拟合法估算本底,用式(1)表示,然后采用非线性最小二乘拟合法求解式(10),调整正交多项式的系数Cj、计算出高斯函数的相关参数。该方法大大提高了谱线本底处理的精确度,但需要用户设置正交多项式的阶数。
正交多项式拟合法中正交多项式的阶数一般由用户根据本底的复杂程度、拟合区间设定。阶数小了,不能够准确地描述本底;阶数大了可能使拟合本底失真,也造成参数过多,显然有一个最佳的阶数。P.V.Espen[11]从统计学角度出发,研究发现如果第n+1阶正交多项式的系数cn+1与它的标准差Scn+1相当,说明cn+1可能使拟合结果失真,如果满足式(9),那么阶数n为最佳阶数。
本文综合上述方法提出阶数自适应型正交多项式模型法:从1阶开始,每次用正交多项式拟合法估算本底,计算最高阶系数Cn的标准差Scn,如果不满足式(9),阶数增加1;如此循环,直到第n+1阶满足式(9),则最佳阶数为n;把具有最佳阶数式(1)代入式(10),用L-M(Levenberg-Marquardt)算法求解,计算流程如图1示。该方法不再需要用户设定多项式阶数,能自动适应各种复杂本底,也减少了多项式中不必要的参数个数,降低了式(10)的自由度,有利于L-M算法的收敛。

图1 自适应正交多项式模型方法流程图
(7)
(8)
|cn|<2Scn
(9)
(10)
2 仿真验证
采用合成谱代替实测谱用于实验,并假设谱线已经光滑处理,统计涨落较小,不以考虑。
为了证明阶数自适应型正交多项式模型法对本底处理的效果,用式(11)~式(13)中的p1~p3和多项式b4构造合成谱区,其中p1~p3是高斯函数,用于模拟谱线特征峰;b4是4阶多项式,用于模拟复杂本底。合成谱区见图2,其中246~372道是感兴趣区(regions of interest,ROI)。
(11)
(12)
(13)
b0=10.44
(14)
b1=0.02j+b0
(15)
b2=2.78·10-3j2+0.75j+b0
(16)
b3=4.3·10-5j3+2.09·10-2j2+2.52j+b0
(17)
b4=-8.57·10-7j4+4.46·10-4j3+
7.33·10-2j2+4.02j+b0
(18)
式中:
i—道址,从241到501;
j—变量,其值为i-240;
p—高斯函数;
b—多项式。
为了比较不同方法对各种曲率本底的处理效果,用p1~p3分别与b1、b2、b3、b4构造出不同复杂程度的本底的合成谱区,分别用SNIP算法、傅里叶变换法、正交多项式拟合法、线性多项式本底模型法、正交多项式模型法和阶数自适应型正交多项式模型法处理这些合成谱的ROI的本底。

(19)
3 结果与讨论
用阶数自适应型正交多项式模型法对图2 ROI的本底进行处理,处理效果如图3所示。计算出正交多项式的最佳阶数为4阶,计算本底与真实本底十分接近,误差在±0.5以内,x2小于0.1。不同方法处理的结果见表1。

图2 合成光谱和感兴趣区
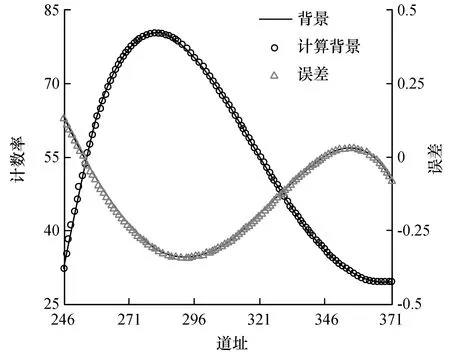
图3 阶数自适应正交多项式模型方法处理本底的结果
从表1可知,对于不同曲率的本底被不同方法处理后的效果差别较大;本底模型法的处理结果整体优于本底估计法。论文介绍的阶数自适应型正交多项式模型法不需用户根据本底设置参数,且对不同曲率本底处理的效果相当;其他方法或多或少需要根据本底的复杂程度调节一些参数,且在复杂本底时处理结果并不理想。

表1 采用不同方法进行处理的不同曲率本底
SNIP算法、傅里叶变换法、正交多项式拟合都把本底当做平缓变化部分(低曲率)、特征峰当作快变化部分(高曲率)处理,并以此为切入点采用各自不同的方式,估计出本底。在伽马能谱测量中,由于环境散射在低能端会形成一个变化较快的本底区域,该区域的本底曲率与环境中的散射材料密切相关[12-13]。另外,在含重叠峰的ROI,原本曲率较高的特征峰由于叠加效果,曲率降低。特别是多个特征峰相邻,且峰面积相差较大时,面积小的特征峰相交区域曲率会严重降低。这样不管是本底曲率高,还是由于重叠效应使特征峰的曲率降低都会造成本底与特征峰的变化率有较大且不可忽略的重叠部分,上述算法很难区分它们。曲率重叠部分越大,本底估计的偏差越大,表1中曲率越高的本底,处理结果偏差越大,就是这个原因。而且这些方法需要根据不同曲率的本底调节参数,才能获取较好的结果。
SNIP算法需要调节迭代次数,傅里叶变化法需要调节截至频率、步进频率,正交多项式拟合法需要调节阶数。这些参数都比较抽象,需要一定的应用经验,而且本底是随着样品成分、测量条件的变化而变化,不利于能谱的批量处理。正交多项式拟合法虽然在本底处理理论上进步不大,但在数值算法上更简单、快捷、容易收敛,而且本底处理结果可以用正交多项式的线性组合表示,为相关的本底模型法提供了有利条件。
线性多项式模型法和正交多项式模型法不再只关注本底与特征峰变化率的不同,而需要建立更加具有物理意义的数学模型,特征峰用高斯函数表示,本底用数学函数表示。该方法充分利用了特征峰的数据,表1中计算结果也更加准确,但依然需要根据本底的复杂程度设置多项式的阶数。从表1可知,不同阶数的拟合结果相差较大。而且线性多项式模型法阶数不能大于4阶[3],大于4阶后拟合结果可能出现振荡,表1中线性多项式为5阶时,结果出现振荡,与真实本底相差很大,因此不能用于谱区间较宽、本底较复杂的情况。
自适应型正交多项式模型法不仅充分利用特征峰的数据,也充分利用了本底数据,数学模型更加完善。在拟合本底时,根据本底的复杂程度自动选择合适的阶数,无需人工设置。而高斯函数所需参数(峰位、标准差),可以通过其它算法自动求得近似值;峰面积是线性参数,初始值并不重要,都能满足L-M算法。因此该方法不需要人工设置参数。表1中,该方法对不同曲率本底处理结果相当,且都比较理想。
4 结 论
阶数自适应型正交多项式模型法建立了更优良的数学模型,充分利用谱数据,能根据能谱本底的特点(复杂度、宽度)自动选取最佳的正交多项式阶数,不管是本底曲率低或高,经过处理后都能获得满意的结果。该模型法不需要用户设置任何参数,为快速、批量处理能谱数据提供了有力的支持,具有实用价值。对于某些能谱段的特征峰可能不太符合高斯响应,要用修正的高斯函数描述,需要进一步研究。
