由一道课本例题说开去

云浮市教育局教研室(527300) 胡明辉

一、课本例题

课本题(必修1)：求函数f(x)=lnx+2x-6的零点的个数.

说明为了解决有关问题,我们给出这一问题的另一种解法.

解函数f(x)的定义域为0.所以f(x)是(0,+∞)上的增函数.又所以,函数f(x)=lnx+2x-6在(0,+∞)上有且只有一个零点.

这是一个简单的单调递增且只有一个零点的问题,可以从以下两个方面解决：

(1)用导数符号说明函数的单调性,解决最多几个零点的问题;

(2)用极限方法说明零点存在定理,解决有没有零点问题.

变式求函数f(x)=-lnx+2x-6的极值点的个数.

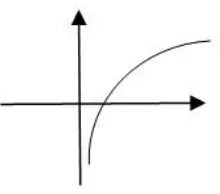
图1

解函数f(x)的定义域为0.所以f′(x)是(0,+∞)上的增函数.又2＞0.所以,在(0,+∞)上有唯一的零点x0(显然).当时,所以,函数f(x)在(0,+∞)上是减函数.当时,f′(x)＞0.所以,函数f(x)在(0,+∞)上是增函数.所以,函数f(x)=-lnx+2x-6在(0,+∞)上有且只有一个极大值点.

上面问题可归结为h1(x)=lnx与另一函数h2(x)的和,是只有一个零点和一个极值点的问题,其解法的步骤为：

(1)对f(x)的导数f′(x)再求导数f′′(x);

(2)判断在给定区间(或其子区间)内f′′(x)的符号,以便确定f′(x)的单调区间;

(3)求f′(x)的极值点,判断f′(x)的符号.

(4)确定f(x)的零点、极值点相关问题.

二、综合运用及方法总结

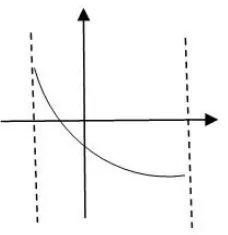
图2

解函数f(x)的定义域为如图1.当时,.即：f′′(x)在上是减函数.又所以,f′′(x)在上有唯一零点,设为x0.当x∈(-1,x0)时,f′′(x)＞0,即：f′(x)在(-1,x0)上是增函数.当时,f′′(x)＜0,即：f′(x)在上是减函数.所以,f′(x)在区间存在唯一极大值点.

2.已知f(x)=ex-ln(x+m).

(1)若x=2是f(x)的零点,讨论函数f(x)的单调性;

(2)若f(x)只有唯一的零点,求实数m的取值范围;

(3)若函数f(x)是定义域上的增函数,求实数m的取值范围;

(4)若函数f(x)的极大值为g(m),求g(m)的值域;

(5)当m≥1时,证明：(其中x1、x2是不相等的正实数).

(6)若x=0是f(x)的极值点,讨论f(x)的单调性;

(7)若f(x)只有2个零点.求m的取值范围;

(8)若f(x)在[0,1]上单调递增,求m的取值范围;

(9)当m＜5-e时,证明：f(x)＞0.

先请看：函数f(x)=ex-ln(x+m)的一个重要性质.

性质f(x)在定义域(-m,+∞)内有唯一的极小值点x0,相应极小值为f(x0),f(x)在(-m,x0)单调递减,在(x0,+∞)单调递增.

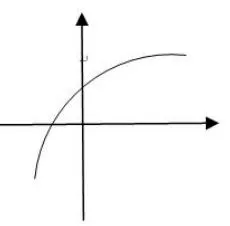
图3

证明由于可知在(-m,+∞)是增函数,注意到+∞,如图2.故f′(x)在(-m,+∞)上有唯一零点,且x∈(-m,x0)时,f′(x)＜0,f(x)单调递减;x∈(x0,+∞)时,f′(x)＞0,f(x)单调递增;从而x0为f(x0)的唯一极小值点,相应极小值为f(x0).

利用上面性质,容易解决上面问题.

已知f(x)=ex-ln(x+m).

(1)若x=2是f(x)的零点,讨论函数f(x)的单调性;

解f(2)=e2-ln(2+m)=0,解得设方程的唯一解为x0(无法求得精确值,近似值为-7.383),故f(x)在单调递减,在(x0,+∞)单调递增.

(2)若f(x)只有唯一的零点,求实数m的取值范围;

解由性质2可知若f(x)只有唯一的零点x=x0,则x=x0也是其极值点,从而有从而x0+m是方程的根,容易证明该方程有唯一的根且位于(1,2)内,近似值为1.763,于是可知故存在唯一的实数m使得若f(x)只有唯一的零点,m∈(2,3),近似值为2.33.

(3)若函数f(x)是定义域上的增函数,求实数m的取值范围;

解由性质2而可知不存在满足要求的实数.

(4)若函数f(x)的极大值为g(m),求g(m)的值域;

解由性质2可知f(x)不存在极大值,只有极小值,分别作出y=ex和y=ln(x+m)的图像,可知当m→+∞时,ex-ln(x+m)的最小值趋向-∞;当m→-∞时,ex-ln(x+m)的最小值趋向+∞;故极小值g(m)的值域为.

(5)当m≥1时,证明：(其中x1、x2是不相等的正实数).

证法一利用函数凹凸性与二阶导数的关系恒成立,故结论成立;

证法二直接用定义法来证注意到于是由基本不等式得从而上述式子成立;性质1得证.

(6)若x=0是f(x)的极值点,讨论f(x)的单调性;

解由解得m=1,由性质2可知x0=0,从而f(x)在(-1,0)单调递减,在(0,+∞)单调递增.

(7)若f(x)只有2个零点.求m的取值范围;

解只有2个零点则极小值必须小于零,由(2)可知极小值等于零时m的临界值为m0=t0+lnt0,其中t0为方程的根(t0近似值为1.763,m0的近似值为2.33),故f(x)只有两个零点时所求的取值范围是m＞m0.

(8)若f(x)在[0,1]上单调递增,求m的取值范围;

解f(x)在[0,1]上单调递增0对任意x∈[0,1]恒成立.利用分离参数得得从而故所求的m的取值范围是[1,+∞).

(9)当m＜5-e时,证明：f(x)＞0.

解由(2)(7)可知f(x)没有零点时必有f(x)＞0恒成立,且此时m＜m0,m0=t0+lnt0,其中t0为方程的根(t0近似值为1.763,m0的近似值为2.33),注意到从而结论成立.

三、问题拓展

有的函数f′(x)=0无法求解,但是再求导数后,[f′(x)]′=0的根却容易求出来,此时可以利用[f′(x)]′的性质反推得出f′(x)的单调性和最值,再利用f′(x)的单调性和最值得出f(x)的单调性和最值.这类函数较常见的有为关于x的代数式,通常是有理函数)等.

分析令虽无法求解,但e-x-1＜0,故f′(x)为(0,+∞)内的减函数,f′(0)=0,从而f′(x)＜0在(0,+∞)恒成立,即f(x)为(0,+∞)内的减函数,f(0)=0,于是易得到对任意

2.证明：对任意正数x,都有

分析令显然只需证明f(x)＞0在(0,1)成立.注意到,可以判断在(0,1)递增且有唯一零点x0,x0为f(x)在(0,1)的最小值点,再对极值点代换可证f(x0)＞0.

分析,对影响y′符号的因子ex-1(x-3)+(x+1)单独分析,令g(x)=ex-1(x-3)+(x+1),g′(x)=ex-1(x-2)+1,[g′(x)]′=ex-1(x-1),从而g′(x)是[0,1)的减函数,g′(1)=0,故在[0,1)上g′(x)＜0,g(x)是[0,1)的减函数,g(1)=0,从而0≤x＜1有g(x)＜0,y′=的最大值为

4.设0＜a＜1,函数现给出以下结论：

①f(x)可能是区间(0,1)上的增函数,但不可能是区间(0,1)上的减函数;

②f(x)可能是区间(0,m)上的减函数;

③f(x)可能在区间(0,1)上既有极大值,又有极小值.

其中正确结论的序号是____.

解.设g(a)=则当时,g′(a)＜0,即：g(a)在上单调递减.当时,g′(a)＞0,即：g(a)在上单调递增.所以,当时,g(a)取得最小值固g(a)＞0,即当时此时f(x)在(0,1)上单调递增.所以,f(x)可能是区间(0,1)上的增函数,但不可能是区间(0,1)上的减函数.即：①正确.因为所以,f(x)不可能是区间(0,m)上的减函数.即：②错误.当a=e-2时,故存在使得此时,f(x1)是极大值,f(x2)是极小值.故③正确.

总结对于有一个极值点和至多两个零点的问题,此法比较有效.