巧用化归“提高”解题能力
——以几类典型问题为例
2020-01-02江苏省大丰高级中学224100张振敏
江苏省大丰高级中学(224100) 张振敏
在解决问题时我们常常遇到“新”问题,学生往往“云里雾里”,没有思路.但如果能够“巧”用知识迁移,转化为已熟悉的问题,不仅找到解决问题的思路,还能化繁为简,大大减少思考和计算难度,做到快速准确的解决问题.
化归是将面临的新问题转化为熟悉的规范问题的中学数学中的常见思想方法[1],它包括化归对象、化归目标、化归途径三要素.化归的关键是化归对象与化归目标的联系,往往需要善于观察和辨别新问题的特征并寻找其本质属性,进而与“旧”知识本质属性对应,常常用到分割图形,特殊化与一般化、数形互化、换元、消元、等方法.化归的一般过程[2]如下图1:
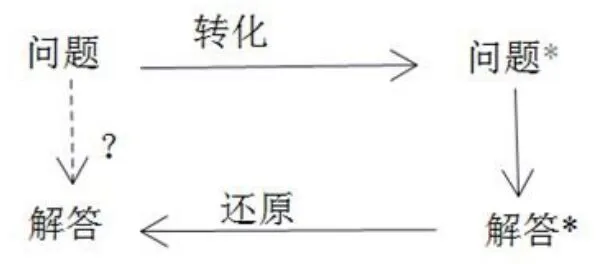
图1
一、方程问题
例1解方程
分析这是个无理方程的问题,一般解法是两次移项,两次平方,但计算量很大,也容易出错.观察例1中两个无理根式的特征,经过变形得即两个根式互为倒数,通过换元则原方程化归为规范的一元二次方程.
解原方程可化为
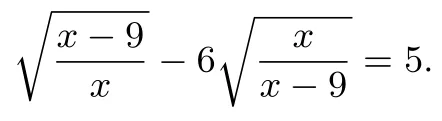
令

说明解无理方程通常是把它化归为有理方程,平方的过程容易产生增根,因此解分式方程和无理方程式要验根.方程的化归首先要有丰富的知识储备,对无理方程、分式方程以及换元法熟练掌握;其次要善于观察问题,必要时适当变形,把原问题的特征凸显出来,寻求化归目标,进而建立化归对象与化归目标的联系.
例2设的值.
分析这里的问题是已知三个数的和以及它们倒数的和,求三个数的平方和,把问题特殊化,容易联想到已知

求x2+y2=?的问题,把②变形为平方后即可求解.
解设令


即nt+mt+mn=0.所以

说明对于高次方程或多元方程,一般通过特殊化与一般化、整体代换等思想把高次化为低次、多元化为一元或二元.同时需要要有善于观察问题的结构特征,即三个分式的和是1,三个分式的倒数和为0,让求三个实数的平方和,这和两个数的和与它们的倒数和形式的计算有很很多特征一样;二是化归应把原问题化归为已熟悉的规范问题,这需要对方程、求两个数的平方和、配方法熟练的掌握,否则很难建立两者之间的联系化归很难实现;最后需要多思考,积极尝试一题多解、一题多变的训练,这样不仅可以把知识记忆牢固,还可以提高发散思维能力.
二、几何问题
例3如图2-1,设ABCD为任意四边形,E,F将AB分成三等份,G,H将CD分成三等份,求证:

图2-1
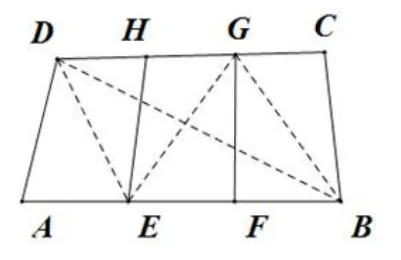
图2-2
分析(1)显然需要连接EG,将四边形EFGH分成两个三角形,于是易得进而寻找四边形EBGD与ABCD的关系,最终可得到结论.
证明连接EG,将EFGH分成两个三角形,连接DE,BG,则

因而

于是
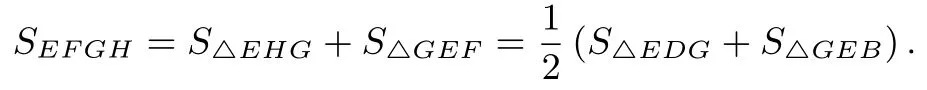
连接DB,将EBGD分割成两个三角形,由于

说明解面积、体积的计算或证明中,经常用到分解法和构造法.分解法是把考虑问题按需要分解成若干部分使其容易求解,有时需要把分解后的问题重新组合;构造法是通过做辅助线、平移、翻转等过程把隐含条件凸显出来.如例3,通过连接BD,DE,EH等辅助线把不规范的四边形构造成规范的三角形和四边形,从而达到化归的目的.
例4求的最大值.
分析题目中含有根式,并且根式里面为两个完全平方式的和,这样的问题比较棘手,但仔细观察每个根号里平方差中都有x和x2,若能联想到两点间距离公式,即到A(3,2)与B(0,1)的距离之差的最大值,利用数形结合与及三角形边的的性质,问题就迎刃而解.
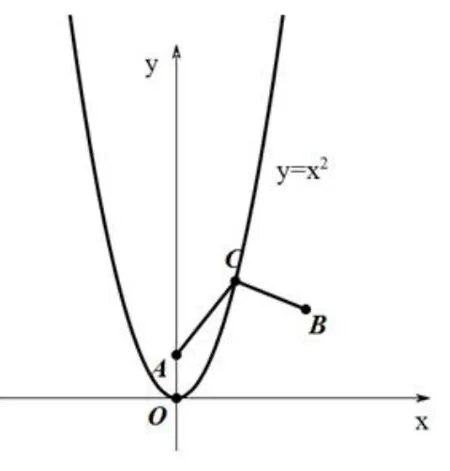
图3
解由题意知,如图3所示,上述问题可看成即到A(0,1)与B(3,2)的距离之差的最大值,而C是二次函数y=x2上的点,由图像知,CB-CA的最大值为线段AB..
说明代数问题几何化以及几何问题代数化是中学中常见的化归技巧,巧用化归不仅使复杂的代数问题转化为规范的几何问题,而且使复杂的几何证明直观化、代数化,避免复杂的几何证明.例4中的问题看似代数问题,但仔细推敲,发现它与距离的差有相似的之处,因此联想到数形结合的思想,画出图像后发现这是二次函数上的点到定点距离之差的最大值,这需要很强的发散思维.
三、不等式问题
例5求证.
分析观察不等式左边和右边,左边第n项的分母为分子为1的n项的和;右边为可以变形为

通过相邻两项分子有理化得到
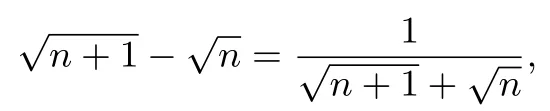
然后经过放缩即可得到结论.
证明由

可得
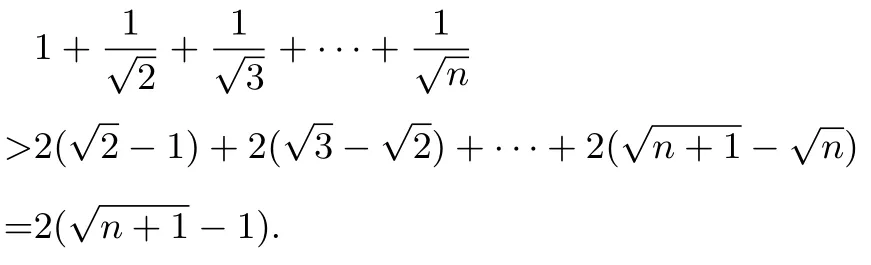
说明在不等式计算或证明中,人们常用分析与综合法,通过观察条件和结论的特征,从熟悉的一方入手,通过适当的等量变化达到证明的目的;也可同时从条件与结论入手,寻找连接两者之间的桥梁.有时需用到放缩法舍去一些与问题无关的项,从而快速的解决问题的目的,如本题需要熟练掌握
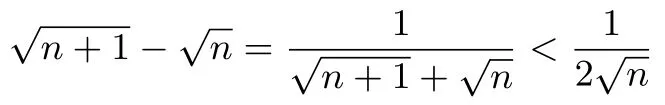
作为桥梁,否则问题是不好解决.
四、解析几何问题
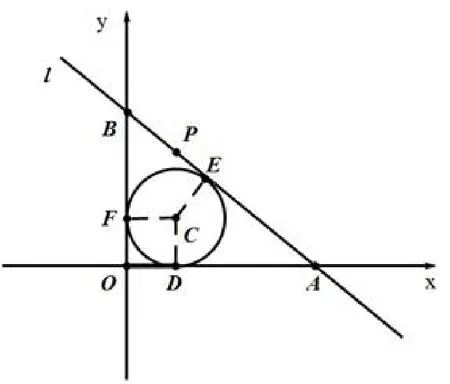
图4
例6如图4直线l经过P(1,3)与x轴的正半轴交于点A,与y轴交于点B,且三角形OAB内切的圆半径为1,求直线l的解析式.
分析显然可设出A和B的坐标,利用切线的性质很容易把△OAB的周长和面积求出,由等面积法得到ab=2a+2b-2,接着由△OAB~△DAP,进而得到.化归为解二元一次方程组问题,进而求出A,B两点坐标,接着用待定系数法解出直线l的方程.
解设A(a,0),B(0,b),则
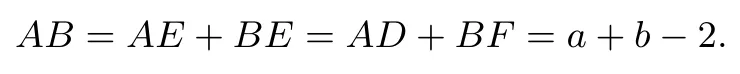
由

得ab=2a+2b-2.由△OAB~△DAP,从而
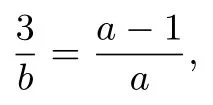
即ab=3a+b.联立方程
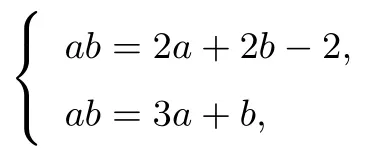
解之得
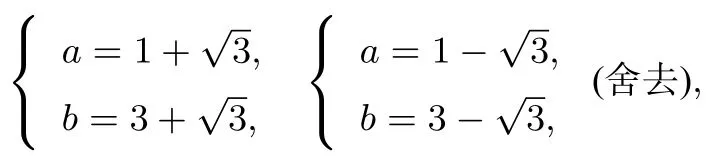


解之得

说明这个题目的关键是通过设未知量的方法把已知条件“不足”的问题化归有充足条件的问题,通过数学推理和计算进而建立二元一次方程组,把设出的未知量解出.观察本题也可以E点为突破口,通过三角形相似解出E的坐标,进而利用待定系数法求出直线的方程.
总结化归的核心思想是“变”,这种“变”往往就是解题的一个思维过程,即在解决问题时经过的思索.化归的过程是对问题认识和归类活动的过程;是对问题不断分析综合的过程;是思维定式与突变统一的过程.化归的目的是将未知化为已知,复杂化简单的过程,但并不是所有的问题可以化归,因此在化归时应积累大量经验.否则造成引入歧途,有碍问题的解决.总之化归无论在初中教学和解决问题还是在知识梳理中都扮演者重要的角色,它不仅是教师教学中必备的方法,巧妙利用化归加深学生对知识的理解,达到理想的教学目的,而且是学生解决问题常用到的方法,巧妙的化归往往达到事半功倍的效果.
