构造可导解析函数常见类型例析*
2019-12-31甘肃省兰州市第四十五中学730070波甘肃省兰州市第六十九中学730094魏国斌
甘肃省兰州市第四十五中学 (730070) 宋 波甘肃省兰州市第六十九中学 (730094) 魏国斌
近年来,高考数学试题和模拟题的客观性试题中常出现构造可导解析函数的问题,它旨在考察学生熟练掌握函数的求导公式和法则的基础上,通过逆向思维构造可导解析函数的能力,这类试题因思维含量高,综合性强,难度大,故不易求解,已逐渐成为高考客观性试题中的热点和难题.要解决这类问题,需要熟练掌握一些特殊解析函数的导函数,即能通过求导公式和法则构造这些特殊导函数的原函数,从而使问题迎刃而解.下面例析构造可导解析函数的四种常见类型,供大家参考.
类型一 若f′(x)=ex,则构造f(x)=ex+C(C为常数).
例1 函数f(x)在其定义域内满足xf′(x)+f(x)=ex,且f(1)=e,则函数f(x)的极值情况正确的是( ).
(A)有极大值,无极小值
(B)有极小值,无极大值
(C)既有极大值又有极小值
(D)既无极大值又无极小值
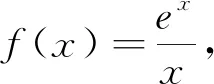
类型二:若f′(x)=xex,则构造f(x)=(x-1)ex+C(C为常数).
例2 若函数f(x)满足xf′(x)-f(x)=x3ex,且f(1)=0,则当x>0时,f(x)( ).
(A)有极大值,无极小值
(B)有极小值,无极大值
(C)既有极大值又有极小值
(D)既无极大值又无极小值
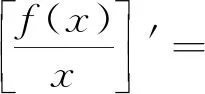
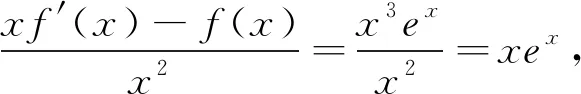
类型三 若f′(x)=lnx,则构造f(x)=xlnx-x+C(C为常数).
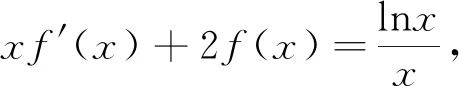
(A)有极大值无极小值
(B)有极小值无极大值
(C)既有极大值又有极小值
(D)既无极大值也无极小值
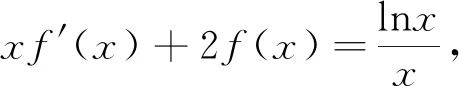

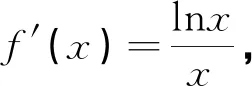
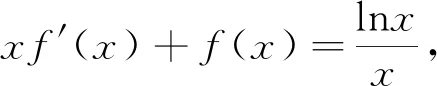
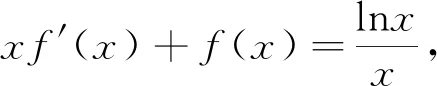
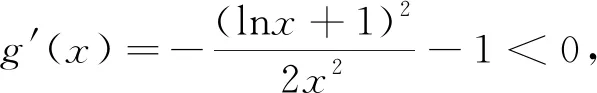
简单的正向应用求导运算法则仅仅考查了学生对法则的掌握,而在此基础上构造可导解析函数,则更能检阅学生对求导运算的全方位把握,更能体现出数学思维的双向变通.正因为如此,考查构造可导解析函数应用的试题倍受命题者的青睐,意在考查学生熟练掌握求导法则应用的能力和灵活、变通应用的能力.
