2016年山东省20题第(Ⅱ)问的三种解法
2017-01-09张业山苏凡文
数理化解题研究 2016年34期
张业山● 苏凡文●
山东省宁阳一中(271400)
2016年山东省20题第(Ⅱ)问的三种解法
张业山● 苏凡文●
山东省宁阳一中(271400)
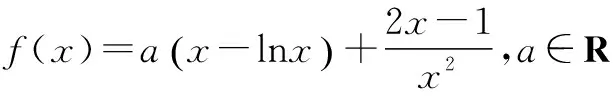
(Ⅰ)讨论f(x)的单调性;
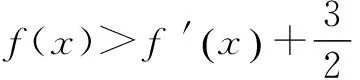
解析 (Ⅰ)当a≤0时,f(x)的增区间为(0,1),减区间为(1,+∞);
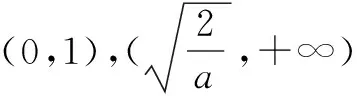
当a=2时,f(x)增区间为(0,+∞);
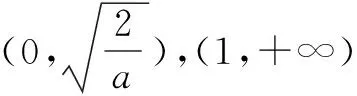
(Ⅱ)方法一 作差法
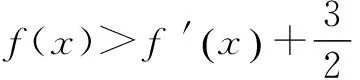
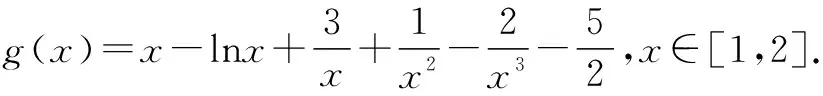
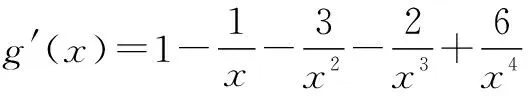
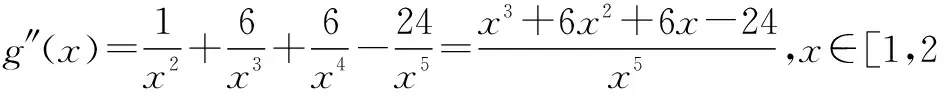
令h(x)=x3+6x2+6x-24,显然h(x)在[1,2]上为增函数.
因为h(1)=-11<0,h(2)=20>0,所以∃x1∈(1,2),使得h(x1)=0.
所以x∈(1,x1)时h(x)<0,g″(x)<0,g′(x)为减函数;x∈(x1,2)时h(x)>0,g″(x)>0,g′(x)为增函数.

∃x2∈(1,x1)使得g′(x2)=0.
所以x∈(1,x2)时,g′(x)>0,g(x)为增函数;
x∈(x2,2)时,g′(x)<0,g(x)为减函数.
所以g(x)min=min{g(1),g(2)}.
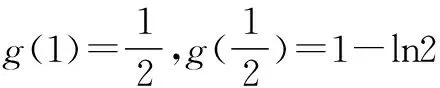
所以g(x)min=1-ln2>0.
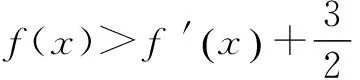
解法二 最小值大于最大值
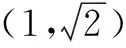


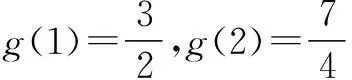
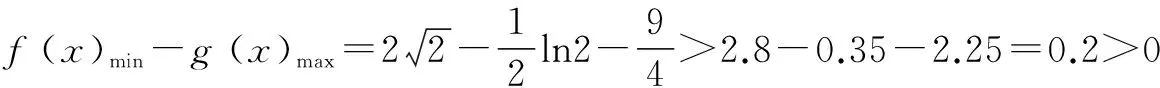
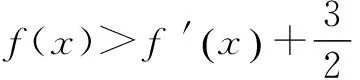
方法三 放缩法
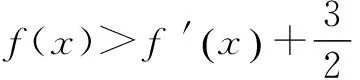
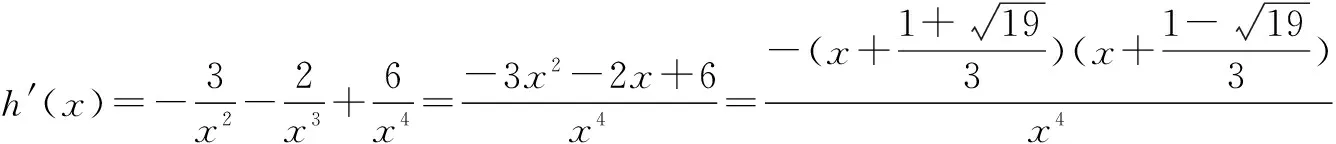
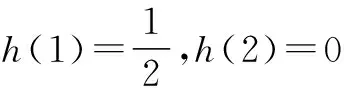
即g(x)≥0,当且仅当x=1时取等号;
h(x)≥0,当且仅当x=2时取等号.
因为等号不能同时取,所以g(x)+h(x)>0,
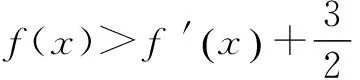
G632
B
1008-0333(2016)34-0007-01
