近年来高考数学文化试题统计与分析

顺德容山中学(528303) 胡 萍 马崇元

数学文化是人类文明的重要组成部分，数学文化的蓬勃发展与应用正符合当下社会的需求.《普通高中数学课程标准(2017年版)》在课程性质、基本理念、课程目标、课程结构、课程内容中明确指出“要注重数学文化的渗透”[1]，通过数学文化不仅可以让学生感受数学的文化与精神，同时也有助于学生对数学概念和思想方法的理解，激发学生学习数学的兴趣.在“关于政协十二届全国委员会第五次会议第1703号(教育类164号)提案答复的函”中提到，2017年高考多渠道落实立德树人根本任务，全方位弘扬中华优秀传统文化.数学科试题加强中国古代数学文化的渗透，强调中国古代数字文化的传统特色[2].

近几年，无论是全国卷还是自主命题的地方高考卷，数学文化背景下的试题都屡见不鲜，数学文化高考试题不但能较好的考查学生的数学知识、阅读能力和创造能力，又能丰厚学生的数学文化底蕴和数学核心素养[3]，能有效地考查学生在新的情境下对知识的理解以及对题目抽丝剥茧的能力.通过对近五年高考数学文化试题的统计与分析，不仅有助于教师、学生高考的备考，同时对数学课程和教学改革均具有积极的导向和促进作用[4].

1.1 高考数学文化试题分布高考中的数学文化试题牵动着无数人的心，以下是对近几年全国卷和湖北省中的数学高考题进行分析，统计高考题中数学文化试题的分布情况.见下表：

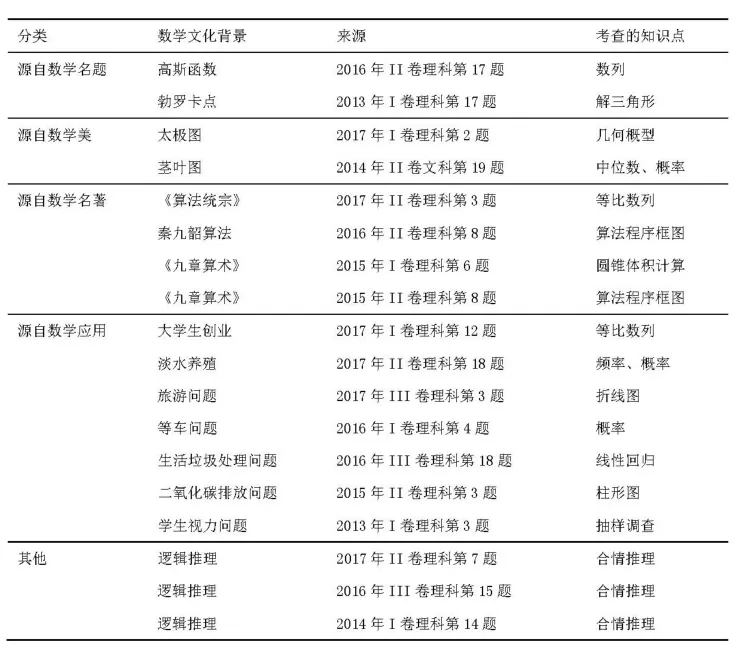
表1 近年全国卷高考数学文化试题分布

从上述表格来看，数学文化越来越受到重视，2013年到2014年，以数学文化为背景命题只在卷I出现，而从2016年到2017年，卷I、卷II、卷III都有出现.近5年的全国高考数学文化试题中数学名著和数学应用为文化背景的居多，并且大部分分布在选择题.结合数学文化考查的内容也多样化.这与国家积极弘扬我国古代的数学文化息息相关，并且强调数学与社会接轨，与生活接轨，做到真正的学以致用.

这是全国卷的情况，我们再来看看湖北省的高考数学文化试题的情况.见下表：

表2 2011-2015湖北省的高考数学文化试题分布

自2015年以后，湖北省取消了高考自主命题。从2015年往前看近5年的湖北省的高考数学文化试题，纵向看，每年渗透数学文化的试题，所占的份额不小.可见湖北省对数学文化的重视程度之高，出自的数学文化背景较多，有我国古代的，也有国外的.这些题放在填空题居多，考查的知识点不一.

不管是全国卷还是湖北卷的高考题，数学文化试题都是占有一席之地的.随着数学文化的关注度越来越高，会有更多的省份加入关注和重视数学文化的队伍.期待数学文化特别是中国的数学文化得到更好传承和发展.

2.2 高考数学文化试题的背景归类

高考数学文化试题的来源甚广，背景也不尽相同，本文仅从四个背景方面论述，分别从源自数学名题、源自图形美、源自数学名著、源自数学应用进行论述.对上述两个表格进行统计，见下表：

表3 历年高考数学文化试题

2.2.1 源自数学名题

以数学名题为文化背景的高考试题是高考数学文化试题中的一大特色.这些名题一般与著名的数学家联系紧密，或者与著名的数学定理、公式、图形等相关，或者有相似的经典解法.这些数学名题经过长期的积累和不断的创新，得到很好地拓展.这也是数学名题深受出题者喜爱的原因.

真题1(2016年全国卷II数学理科第17题)Sn为等差数列{an}的前n项和，且an=1，Sn=28，记bn=[lgan]，其中[x]表示不超过x的最大整数，如[0.9]=0，[lg99]=1.

(I)求b1,b11,b101;

(II)求数列{bn}的前1000项和.

本题主要考查数列的内容，它的文化背景是高斯函数，说起高斯函数，我们会自然而然地想起被誉为数学王子的著名数学家高斯，高斯有一个很有名的数学故事：从整数1加到100的故事.高斯函数又名为取整函数，[]就是取整符号，题中[x]就是取整函数.由高斯函数得到整数数列，进而求出第n项的数和前n项和.

真题2(2013年湖北卷数学理科第14题)古希腊毕达哥拉斯学派的数学家研究过各种多边形数，如三角形数1,3,6,10，···，第n个三角形数为记第n个k边形为N(n,k)(k≥3)，以下列出了部分k边形数中第n个数的表达式：

正方形数N(n,4)=n2，

六边形数N(n,6)=2n2-n，

······

可以推测N(n,k)的表达式，由此计算N(10,24)=____.

本题的数学文化背景源自毕达哥拉斯形数，本题主要考查数列的通项公式.本题对学生的归纳能力要求较高，在已给出的几种形数中找到规律，就要学生大胆地想象、猜测.形数可以说是数与形的结合，让学生感受别样的数形结合.

真题3(2012年湖北卷数学理科13题)回文数是指从左到右与从右到左读是一样的正整数.如22,121,3443,94249等.显然 2位回文数有9个：11,22,33，···，99，3位回文数有90个：101,111,121，···，191,202，···，999.则

(I)4位回文数有_____个；

我们看2位回文数，第1与第2位是一样的，实际上取决于第1位的数，第1位可取1～9这9个数，所以2位回文数有9个.再看3位回文数：第1位与第3位的数是一样的，实际上3位回文数取决于第1,2位，中间第2位可取0～9这10个数，第1位可取1～9这9个数，然后排列组合得到90个数.而4位回文数取决于前2位数，即：10～99这90个数.所以有2n位回文数有即9×10n个，2n+1位回文数有即9×10n个.

本题的文化背景源自回文数，主要考查的是排列组合的内容.本题不仅考查了学生的观察和推理的能力，还考查了学生的分类讨论和归纳的能力，同时也让学生感受到数学的神奇之处.

2.2.2 源自图形美

中国古代图形源自生产生活，源自远古人类对事物的直观表象的描述，从而形成简单的几何图形.中国古代人对图形的对称特别讲究，对圆有着极致的追求，寓意事物都有两面，而人们不断地追求其中的平衡点，追求圆满、完美.古代的八角楼，赵爽弦图、杨辉三角、太极图、八卦图、月在各处的形状等，这些图形体现着中国古代人们对自然细致观察的成果，彰显着古代人的智慧.数学中还有另类的图形，如茎叶图、几何图形化和数学文字形化的蝴蝶定理等.这就是数学的图形美，它自身的魅力被人们所折服.

真题4(2017年全国卷I数学理科第2题)如图1，正方形ABCD内的图形来自中国古代的太极图，正方形内切圆中的黑色部分和白色部分，关于正方形的中心成中心对称，在正方形内随机取一点，则此点取自黑色部分的概率是( )

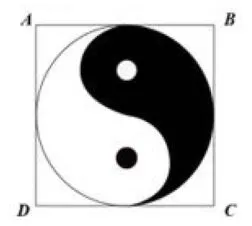
图1

本题的文化背景取自中国古代的太极图，主要考查的是几何概型的内容，本题的几何概型与面积有关，而太极图是一个极致对称的图形，求黑色部分的概率就变得很容易了.用太极图来考查几何概型，一方面展示了太极图的几何构造，另一方面又展示了太极图的对称美，体现了中国古代人对圆的喜爱和对图形对称的审美观.

真题5(2014全国卷II数学文科第19题)某市为了考核甲、乙两个部门的工作情况，随机访问了50位市民，根据这50位市民

图2 记录甲、乙部门工作情况的茎叶图

(I)分别估计该市的市民对甲、乙部门评分的中位数

(II)分别估计该市的市民对甲、乙部门的评分高于90的概率

(III)根据茎叶图分析该市的市民对甲、乙部门的评价

本题的文化背景来自茎叶图，主要考查的是中位数和概率。茎叶图也称枝叶图，是著名的统计学家约翰托奇设计出来的.茎叶图能保持数据的原始性、全面性；并且数据可随时添加、记录，这就体现了茎叶图的便利性，实用性.这是茎叶图的两大优点.用茎叶图来记录市民对甲、乙部门的评分，能很真实地反映甲、乙两个部门的工作情况.数学的美是无处不在的，数学的美也是千奇万化的，茎叶图就体现了数学的奇异美.

2.2.3 源自数学名著

我国古代的数学名著有《数书九章》、《算法统宗》、《九章算术》、《算数书》等，主要是收集或记录生活中的一些数学问题和解决方法.在高考数学试题中以此为文化背景命题的试题，所占的比重较大，特别是全国卷.2013年—2017年的全国卷中，每年都有涉及.

真题6(2017年全国卷II数学理科第3题)我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层的灯数是上一层灯数的2倍，则塔的顶层共有灯( )

A.1盏 B.3盏 C.5盏 D.9盏

本题以数学名著《算法统宗》为文化背景，主要考查的是等比数列的知识点，由题目可以知道这个等比数列的公比，又知道了前7项和，根据等比数列的前n项求和公式，不难求出塔顶层的灯的盏数.本题由《算法统宗》引出等比数列，也就是说在我国古代就已经有人意识到等比数列的应用，可见古代人们的智慧非同一般.

真题7(2014年湖北卷数学理科第2题)我国古代数学名著《九章算术》有“米谷粒分”题：粮仓开仓收粮有人送来米1534石，验得米内夹谷，抽样取米一把，数得254粒内夹谷28粒，则这批米内夹谷约为( )

A.134石 B.136石 C.338石 D.1365石

本题的数学背景来自《九章算术》中的“米谷粒分”，主要考查比例计算.古代人舂米技术还很粗糙，米中夹谷的现象比较常见，古代人对于推测米中夹谷多少，就意识到可以用抽样调查的方法，然后用比例计算推测出粮食的质量，可见古代人的智慧.

真题8(2014年湖北卷数学理科第8题，文科第10题)《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土，这是我国现存最早的有系统的数学典籍，其中记载有求“囷盖”的术：置如其同，令相承也，又以高乘之，三十六成一.该术相当于给出了有圆锥的底面周长L与高h，计算其体积V的近似公式它实际上是将圆锥体积公式中的圆周率π近似取3，那么近似公式相当于将圆锥体积公式中的π近似值取为( )

本题的数学文化背景是《算数书》，主要考查圆锥体积计算.《算数书》是一部数学问题集，全书的内容分为两类：一类是整数和分数的四则运算法则，另一类是跟当时的生产生活实际密切相关的各种应用题及解法.本题由《算数书》引出圆锥的体积计算本题的体积近似公式又有L=2πr，实际上就是求π的近似值，则的近似值就求出来.而本题中“囷盖”很贴切生活，在农村就较为常见，让学生感受到生活处处有数学.

2.2.4 源自数学应用

也有一部分高考试题是以数学应用为背景的，体现了数学的实用性。

真题9(2017年全国卷I数学理科第12题)几位大学生响应国家的创业号召，开发了一款应用软件，为激发大家学习数学的兴趣，他们推出了“解数学题获取软件激活码”的活动，这款软件的激活码为下面数学问题的答案：已知数列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16，···，其中第一项是20，接下来两项是20，21，再接下来的三项是20，21，22，以此类推求满足如下条件的最小整数N：N＞100且该数列的前n项和为2的整数幂，那该款软件的激活码是( )

A.440 B.330 C.220 D.110

本题以大学生创业为文化背景，主要考查数列的内容。大学生创业是当下热门的一个话题，身处大四的学生就深有感触了，国家也在积极鼓励大学生创业，并且有一定的扶持力度.

综上所述，高考数学文化试题的出现，丰富高考试题的样式，为高考注入新的活力，同时也因为这些试题，让数学文化得以传播和关注.数学教师一方面，挖掘教材中许多专题的独特文化背景，利用问题、方法的背景或者产生的曲折历程，创设充满浓郁数学文化的教学问题情景．另一方面，借助数学文化突破教学难点.通过合理使用丰富多彩的数学文化课堂教学模式从而能引起学生的兴趣，激发学生的求知欲，进一步提升学生的数学学科核心素养，为学生的可持续发展和终身学学习打下基石的基础。