适当处理教材，提高学生数学核心素养*

广东省中山市南头镇初级中学(528427) 梁文昌

人教版初中数学课标教材于2004年秋起在全国课程标准教材试验区开始使用.使用至今,对教材的比较、争论之声不断.目前,我校三个年级都在使用人教版初中数学教材.本人是一名基层学校的普通初中数学教师,教学已16年有余,使用过华东师范大学和人教版两个版本的教材,孰好孰坏,实在不是三言两语可以讲得清楚.本文通过案例阐述了在实际教学中对教材取舍的具体做法,希望我们大家都转变观念,不再执着对教材好坏的讨论,而是投入到如何真正使用好教材上来,实现学生数学核心素养的提高.

与传统初中数学教材相比,新人教版初中数学教材中,采用了循序渐进、螺旋上升的设计,对知识点的阐述是由浅入深、逐级递进,顺应了学生的认识心理规律,删减了许多被认为偏繁、偏难的陈旧内容.例如在代数部分,大大降低了数与式的计算、变形的难度要求;删去了比例及其性质的教学内容;分式方程仅限制在可以化为一元一次方程的范围;删去了无理方程、二次方程组的知识.几何课程删减了射影定理、平行线等分线段定理、圆幂定理;三角函数中仅出现正弦、余弦、正切,没有了余切.

新人教版初中数学教材还新增了许多与实际生活联系紧密的内容.例如大大强化了统计方面的内容;新增了概率方面的知识;不等式中对不等式(组)应用作出了教学要求;函数中引入了分段函数并对自变量取值范围提出要求;几何增加或强化了图形变换的内容要求,增加了视图与投影等内容从而树立教学的动态发展观.

应该说,新人教版初中数学教材能够体现新的课程观、教材观、教学观,以培养学生的创新精神和实践能力为重点,以提高学生的综合素质为目标,适应现阶段教师和学生的需要,有利于促进教师专业能力和水平的全面提高,有利于促进学生主动地生动活泼地学习,有利于促进学生全面发展,是一套崭新的面向全体学生的实验教材.

但新教材也并不是完全优胜,在本人教学实践中,教材的内容应当作以下三方面处理.

1.根据学生整体思维水平,合理删除教材内容

学生学习的内容应当是学生可以理解的、符合学生认知水平的,且可以过渡的.这意味着课堂教学应以重视知识的发生发展过程,使学生学习可以得心应手,对难点的学习可合理地分解为以前熟知的内容.当我们遇到书本上的题目是相当复杂的,且无法通过现阶段学习内容得到的,或者要补充相当多的课外内容时,应当合理删除.

例如,在人教版九年级数学上册“实际问题与一元二次方程”一节中,有一道设计图书封面的探究题(可算例题)(见课本P47探究3)：如图,要设计一本书的封面,封面长27cm,宽21cm,正中央是一个与整个封面长宽比例相同的矩形．如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左右边衬等宽．应如何设计四周边衬的宽度(结果保留小数点后一位)?

解这道题需要运用比例的知识,其过程并不简单,而人教版的教材中又删去了比例知识的教学,仅在八年级数学下册书第16章最后的“数学活动”中的“活动1探究比例的性质”(见人教版八年级数学下册P34)中有所涉及,并没有安排任何习题,得出上述结果所需用到的等比性质也并无提及,学生很难得出结论,把其中的道理弄清楚,可能一节课也不够用,而关于面积的例题在教材前面也有,所以这道题就可以大胆舍去.

又例如八年级下册P97《19.2.3一次函数与方程、不等式》一节中,问题3 1号探测气球从海拔5m处出发,以1m/min的速度上升,与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.两个气球都上升了1h.

(1)用式子分别表示两个气球所在位置的海拔y(单位：m)关于上升时间x(单位：min)的函数关系;

(2)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?

这是题目的本意是从函数的角度看解二元一次方程组,观察两个一次函数图象的交点,得到对应方程组的解,这是本节课的难点所在.我觉得它的不合理之处有两个：一是它以应用题的形式出现,学生能通过信息列出函数关系式的已经不多了;二是它是结果为(20,25),这个结果以学生平时习惯1个单位长度为1的情况,基本上没几个学生可以把函数的交点画出来,那又怎么说明数和形的对应关系呢?经过多年课堂经验告诉我们这种题不能让学生在课堂上完成.

2.贴近学生生活与兴趣,适当修改教材内容

学生学习的内容应当是现实的、有意义的且富有挑战性的.这意味着课堂教学应以学生的周围世界和生活实际为探究对象.教师要善于对教学内容进行改编和加工,使教材变得生动活泼,更贴近学生的实际.

在应用题的教学时,我把人名改成本班同学的名字,把地名改成学生熟悉的街道;在七年级第一章乘方的教学中,我用一个故事《棋盘上的米粒》引入;在教七年级第十章的直方图一节时,我把考察某种大麦穗长的分布情况改为全班数学测试成绩,然后分成60分以下、60—70分、70—80分、80—90分、90分以上5个组来描述数据,事实证明,对自己熟悉的生活情景和小故事,学生很有兴趣,新课的引入和开展也变得自然而顺利.

又例如八年级(下册)第十八章《平行四边形》中,有这样一道例题：菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD.求两条小路的长.

此题完成以后,可以适当改变题目中的条件和结论开展变式教学训练.

(1)将条件“∠ABC=60°”改为“∠BAD=2∠ABC”,求两条小路的长;

(2)将条件“菱形花坛ABCD的边长为20m”改为“两条对角线的长分别为12m和16m,求菱形的周长和面积.

这样的修改,可以使学生立足基础知识,推陈出新,充分挖掘例题、习题的发展功能,将习题做“活”,使练习过程不再是机械演练的过程,而是智慧发展的过程.

3.发展学生认知水平,适当补充教材内容

教育家苏霍姆林斯基说：“教师如果不想方设法使学生产生情绪高昂和智力振奋的内心状态,而只是不动感情地脑力劳动,就会带来疲倦.”所以在现在的知识水平之上,我们可以适当补充教材内容,让学生的认知水平提高到一个新的台阶.

例如,传统教材中,因式分解至少要用一章的篇幅来讲授,新教材中仅设为一节,这样显然是不够的.因式分解的教学是在整式四则运算的基础上进行的,因式分解方法的理论依据就是多项式乘法的逆变形.它不仅在多项式的除法、简便运算中有直接的应用,也为以后学习分式的约分与通分、解方程(组)提供了必要的基础.因此,学好因式分解对于代数知识的后续学习,具有相当重要的意义.所以本人在教授因式分解时,将其分成了四个课时：提公因式法、公式法、分组分解法、综合练习.虽然课时多了,但我相信对学生数学思维的练习是有很大帮助的.

又例如,九年级上册第24章圆,第1课教学圆,第2课教学垂直于弦的直径,凡教完第1节的老师都会有疑惑,布置什么练习呢?要不要留点作业?书后没有相应的例题可选用.教材对于圆的这部分知识内容的处理过于简单了.其实这部分内容及随后的如圆心角、圆周角等知识,是学习圆的有关知识的基础,着急是不行的.教材中仅在练习中设了两个学生都能口答的题目,一道题是让学生说出在操场上画一个半径为5米的圆圈的方法,另一道题则是计算树木年轮的游戏题.这样处理教学内容,有点太随意了,书后仅有一道“证明矩形的四个顶点在同一个圆上”的相关题.教完第2课“垂径定理”,书上除了把旧教材上就有的彰显我国古代造桥技术的赵州桥问题改头换面加以利用,此外,再无例题,练习、习题也不多.这样学生不可能得到必要的训练,往后必然导致学生越来越难学以致学不会,教师也必然是越来越难教.所以在教这部分的内容时,我是这样来上课的：在讲授了垂径定理的内容后,先补充这样一个例题：

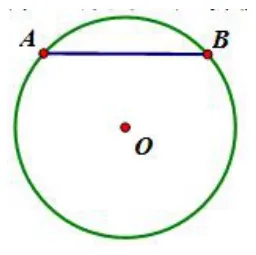
图1

例1已知：如图1,在圆O中：

(1)弦AB=8,O到AB的距离等于3,求圆O的半径.

(2)若OA=10,O到AB的距离等于6,求弦AB的长.

此例题是垂径定理最简单最直接的应用,学生易于接受,对定理的内容也会有更深的理解.在讲授这个例题之后,再来讲书本上赵州桥问题这个应用题,学生就不会觉得太突然.课后练习也补充了一道题：

如图2所示,已知AB为⊙O的直径,且AB⊥CD,垂足为M,CD=8,AM=2,则OM=____.

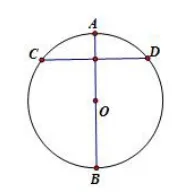
图2

这道练习与书本例题解法相同,要用到方程的思想,但计算更加简单,是对垂径定理的巩固.

再例如,代数中的“判别式”、“韦达定理”堪称与艺术中的芭蕾、京剧相媲美的经典,有意思、好玩儿有趣儿、既能启迪学生智慧、激发学习兴趣、又能培养学生逻辑思维能力,在高中数学中也经常用到,虽然在新人教版数学教材中被定为选学内容,但拿出一节课来,专门讲一讲这部分的内容也并不为过.

学科核心素养是育人价值的集中体现,是学生通过学科学习而逐步形成的正确价值观念,必备品格和关键能力,数学学科核心素养是数学课程目标的集中体现,是具有数学基本特征的思维品质、关键能力以及情感,态度与价值观的综合体现,在数学学习和应用的过程中逐步形成和发展的数学学科核心素养包括：数学抽象,逻辑推理,数学建模、直观想象数学运算和数据分析六大方面.有句名言说得好,“数学是思维的体操”.数学课主要在于培养学生的逻辑思维能力和有条理地说明道理的能力,而并不在于教会或学会、记住多少知识.无论是新教材还是旧教材,都并不是不可撼动的权威,对教材进行适当的取舍和调整是很有必要的.因为只有对教材进行适当的取舍,才可能实现教学内容与教学方法手段的完善统一,才能使教材的普遍性同本地区教学实践的特殊性实现有机结合,才能最大限度地满足学生对学习内容、教学方法的需求,充分调动教学双方的积极性、提高教学效率.对教材的适当取舍,恰恰是我们仔细地深挖教材、理解教材、吃透教材的表现,是我们对学生负责的表现.