爆轰冲击载荷作用下射孔段管柱动力响应分析

李明飞， 徐 绯， 窦益华

( 1. 西北工业大学 航空学院，西安 710072； 2. 西安石油大学 机械工程学院，西安 710065)

射孔作业过程中常发生射孔段管柱塑性弯曲、封隔器中心管断裂及卡管柱等事故，影响勘探开发进程，威胁设备与人员安全。TLM油田DQ6井、DN2-27井、SC气田L16井等重点探井射孔测试联作结束后射孔段管柱出现了塑性弯曲；TLM油田KS101井、WC1井射孔测试联作封隔器中心管断裂；中石油重点风险探井JM1井、KS2井试油结束后，射孔段管柱和电子压力计托筒卡在井下，被迫拔断管柱，因此无法取得完整的试油资料[1-4]。美国Fort Worth盆地[5]、Arkoma 盆地[6]、墨西哥湾等的油气开采也遇到射孔管柱失效事故。分析认为上述事故为聚能射孔爆轰压力脉动及管柱振动所致。如何搞清射孔爆轰瞬间管柱的动力响应规律，搞清管柱的应力及其传播规律，是亟待解决的问题。

由于问题的复杂性，爆轰冲击作用下管柱动力响应方面的参考文献较少，火炮动力学分析与后坐力分析的方法可以提供参考思路[7-8]，但是其研究基于的初始条件和边界条件与射孔爆轰管柱动态响应均不相同，取得成果无法直接应用。文献[9-10]在准确计算爆轰参数的基础上，应用热力学相关理论，分析射孔段峰值压力、井底“口袋”处峰值压力和封隔器处峰值压力，得到射孔瞬间冲击荷载，作用于管柱，基于管柱屈曲理论分析射孔段管柱的强度安全性，对射孔压力、冲击载荷及强度安全研究做了初步探索。Schlumberger公司采用非连续HP(H法-通过将误差大的网格单元加密成多个子单元实现自适应，P法-保持网格不变，通过改变基函数的阶实现自适应)自适应型有限单元法求解不可压缩流体欧拉方程(Euler equation)和纳维-斯托克斯方程(Navier-Stokes Equations)，采用HP型伽辽金数值方法解决爆轰流体对流扩散问题，结合第一原理求解质量、动量和能量守恒方程，模拟射孔液运动及压力脉动[11-13]。文献[14-15]介绍了Halliburton公司在射孔压力脉动方面的研究——用时间推进有限差分法模拟射孔液与管柱的流固耦合，预测射孔压力脉动。

射孔段管柱的振动分析多集中在有限元模拟及地面实验方面。文献[16]设计了一套射孔段管柱动态载荷地面综合测试系统，文献[17]建立了地面模拟试验测试系统，对射孔段管柱端部压力和加速度响应进行测试。文献[18]研究了射孔测试联做工况下油管-减震器-射孔枪的动态响应机理，将减振器等效为有阻尼和弹簧的系统，根据力连续条件模拟三组件之间的相互作用，并通过水下模拟射孔实验验证。分析了射孔弹装药量、减震器数量、油管长度对油管和封隔器动态响应的影响。Schlumberger公司的Baumann等人利用数值模拟方法分析了冲击载荷下井下管柱和工具的动力响应规律，但是，Schlumberger公司将其射孔压力分析与实测技术视为核心机密[19-20]，其研究的可行性和适用性有待进一步确认。文献[21]采用空间梁单元与弹簧单元求解油套间的非线性接触问题，建立了管柱结构动力模型。应用 ANSYS 软件分析射孔爆轰波作用下管柱径向位移、轴力随井深的变化规律。文献[22]采用理论经验公式和 ANSYS/LS-DYNA有限元软件，分析冲击载荷下射孔管柱动力响应。文献[23]采用时间推进有限差分法对射孔瞬间载荷冲击及管柱动力响应进行了数值模拟分析，指出管柱动力响应以及由此引起的管柱失效是高温高压深井射孔技术面临的重要问题。文献[24]研制了与射孔枪相连的能量吸收减震器，并分析了减震器的存在对管柱振动特性的影响。

综上所述，军工和火工研究所基于的初始条件和边界条件与射孔爆轰管柱动态响应均不相同，射孔爆轰工况更加复杂，取得成果无法直接应用。相关研究的核心技术是“黑匣子”，只提供商业软件，无法获取算法。本文首先基于振动力学悬臂梁理论，建立管柱管柱纵向振动微分方程并求解，得到管柱振动规律理论解。并应用Workbench模块模拟射孔管柱动力响应过程，验证理论算法，阐明射孔管柱动力响应规律，并通过固有频率的对比来验证有限元法的可靠性。分析得到射孔管柱速度、加速度和应力变化规律，可用以指导实际生产；并可为复杂边界条件的水下爆炸理论研究提供参考。

1 射孔段管柱动力学模型建立

射孔段管柱在冲击载荷下的动力响应是一个载荷剧烈、边界条件苛刻、交界面多、流固耦合协同作用的复杂过程，本文应用振动力学悬臂梁理论[25]，考虑管柱自重及轴向冲击载荷作用，建立管柱动力学模型，导出管柱纵向振动微分方程，应用分离变量法[26]求解，得到管柱振动固有频率、主振型及位移响应表达式。

1.1 射孔段管柱物理模型描述

如图1(a)所示，以封隔器处管柱端为固定端，管柱底端为自由端，射孔段管柱可简化为悬臂梁模型。管柱轴线为x轴，原点在封隔器处，垂直向下为正方向。则由达朗贝尔原理可得

(1)

式中：横截面上内力N=EA·∂u(x,t)/∂x，ρAdx·∂2u(x,t)/∂t2为微元上的惯性力；u(x,t)为管柱上距原点x处的截面在时间t时刻的纵向位移；f(x,t)为单位长度管柱的纵向作用力；L为管柱长度；c为黏性阻尼系数；v为相对速度，为x和t的函数 。如图1(b)所示，在管柱上取长度为dx的微元体进行受力分析，ρ为管柱的密度；E为管柱材料的弹性模量；A为管柱横截面积；N为截面上的内力。在式(1)左右两边同时除以ρAdx，得到管柱一维纵向振动微分方程

(2)

图1 射孔段管柱动力学模型Fig.1 Mechanics model of perforating string

1.2 射孔段管柱边界条件和初始条件的确定

封隔器处管柱受到约束作用，位移为零；管柱最底端为自由端，初始应力为零，管柱固定端和自由端处的边界条件分别为

(3)

射孔之前管柱处于静止状态，初始速度为零；自重作用下的管柱会产生一定的伸长，若将自重视为外载荷，管柱处于原长的位置视为管柱的平衡状态，则其初始位移为零，即初始条件为

(4)

2 射孔段管柱固有频率与主振型分析

当管柱所受外载荷为零时，即令式(2)中的f(x,t)=0，得到管柱纵向自由振动方程

(5)

(6)

式中：k为常数。管柱边界条件式(3)和式(6)构成了微分方程的特征值问题，只有当kρ/E>0(即k>0)时，式(6)才有非零解。令k=ω2，ω为正数，求解常系数齐次线性微分方程式(6)，可得管柱振动固有频率和主振型分别为

(7)

(8)

式中：i为正整数(即i=1， 2， 3， …)；fi为各阶固有频率，Hz；ωi为各阶固有角频率，rad/s。

3 冲击载荷下管柱动力响应基本方程分析

将爆轰冲击波沿轴向作用于管柱自由端，将自重视为沿管柱轴向均匀分布的外载荷，则管柱的总外载为

f(x,t)=F(t)δ(x-L)+ρAg-cv(x,t)

(9)

式中：F(t)为冲击载荷随时间变化的函数；δ为单位脉冲函数。将式(9)转化为正则坐标下的广义力为

(10)

将管柱位移响应展开为正则振型无穷级数，可得冲击载荷作用下射孔段管柱动力响应基本方程

(11)

式中：Ui(x)为主振型函数；fi为各阶固有频率；qi为冲击载荷广义力；τ为时间积分变量。结合式(10)和式(11)，可以用数值积分的方法求出管柱的位移响应。作者也考察了横向冲击载荷和扭转冲击载荷的影响，对管柱强度影响不大，从略。

4 射孔段管柱动力响应有限元分析

应用ANSYS有限元软件的Workbench模块，基于有限元瞬态动力学方法，以油田常用的27/8＂×5.51 mm P110油管为研究对象，建立射孔段管柱三维有限元模型，作用井下实测射孔冲击载荷，应用后处理程序提取关键数据，分析管柱的动力响应规律，并通过固有频率的对比来验证有限元方法的可靠性。

4.1 射孔段管柱三维有限元模型的建立

模型管柱长度取20 m，管柱材料的弹性模量为2.06×1011Pa，泊松比为0.3，屈服极为758 MPa，密度为7.85 g/cm3。采用八节点六面体单元，用映射方式对划分网格。封隔器下方3m处有2m长的减震器，作为一节弹簧考虑，如图2所示。管柱有限元模型共有24 160个单元，169 200个节点。

初始时刻管柱仅受自重作用，不考虑射孔液对管柱振动的影响，速度和加速度均为零。通过井下射孔压力监测仪采集管柱脉动压力，该压力为实测得到冲击载荷曲线经线性回归得到的载荷谱，施加于管柱，简化后的载荷曲线如图3所示。

图2 射孔冲击管柱有限元模型图Fig.2 Finite element model of perforated impact string

图3 射孔冲击载荷曲线Fig.3 Curve of perforating impact pressure

4.2 射孔段管柱固有频率解析解与有限元解对比与分析

运用ANSYS模态分析方法，如表1所示，得到射孔段管柱振动的前六阶固有频率，由式(7)计算得到固有频率解析解。可以看出，管柱固有频率的有限元解和解析解相近，平均相对差为4.18%。对于石油管工程，壁厚的制造误差控制在12.5%以内就认为是合格产品[27]。也就是说，有限元解和解析解误差不超过12.5%，即认为满足工程精度要求。说明用有限元瞬态动力响应方法分析射孔段管柱动力响应，满足工程精度要求。

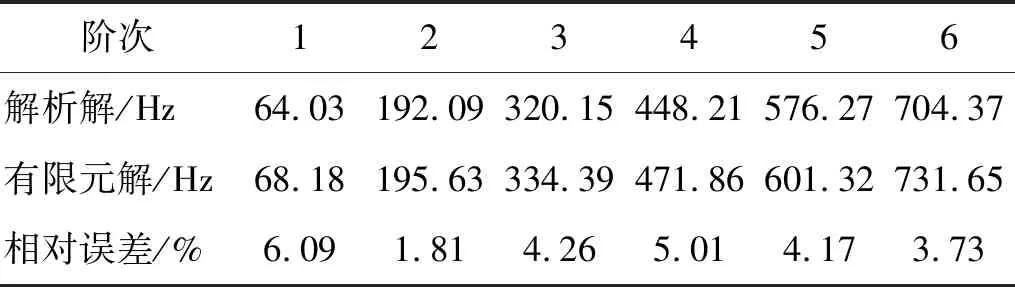
表1 管柱振动固有频率

4.3 射孔段管柱动态位移分析

图4为管柱自由端与固定端位移随时间变化曲线。固定端受到封隔器的约束作用，位移恒为零；自由端受到冲击载荷作用，其位移随时间周期性变化，周期约为15 ms，振动幅度随时间逐渐减小。在0～30 ms，管柱处于压缩振动状态，随后逐渐转变为拉伸振动。9 ms时，管柱压缩长度达到最大值19.2 mm；95 ms时，管柱伸长达最大值9.1 mm，负号表示管柱压缩，正号表示管柱伸长。Sanders等的分析结果表明，无减震器的射孔段管柱压缩50.8 mm，安装减震器后射孔管柱压缩93.9 mm。将本文与Sanders等研究中的管柱截面尺寸、长度、射孔弹炸药装药密度、装药质量、射孔弹数进行比例换算后，本文射孔段压缩折算系数为2.49，射孔段折算压缩48.1 mm，与Sanders等的研究误差为5.3%。采用同样的折算方法，本文与文献[28]的管柱压缩长度相差5.7%。

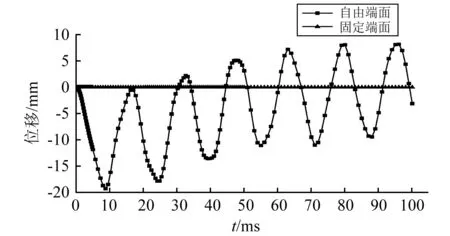
图4 自由端与固定端位移Fig.4 Deformation of constraint end and free end

4.4 射孔段管柱速度与加速度对比与分析

图5为管柱上不同位置振动速度随时间变化的曲面，50 ms内出现了三个速度波峰和三个速度波谷，波峰之间的间隔约为16 ms，最大速度为9.5 m/s。同一时刻，管柱上位置从0 m变化到20 m，振动速度逐渐增大，越靠近封隔器端(0 m处)，管柱振动速度越小。在同一位置，速度随时间周期性变化，越靠近管柱底端，幅值越大。Sofrygina等只是给出了位移随时间的变化关系曲线，据此可以推算出管柱最大速度为1.9 m/s，应用与5.3同样的这算方法，文献[29]折算后的最大速度为8.8 m/s，二者相差7.4%。

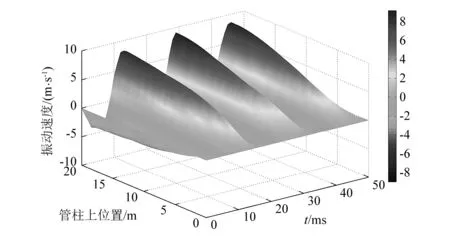
图5 管柱振动速度随时间变化曲面Fig. 5 Curves of the vibration speed of pipe string with time

管柱上不同位置处加速度响应曲面如图6所示，在50 ms内出现三个加速度波峰，加速度峰值约为3 500 m/s2，波峰之间的时间间隔约为16 ms。0 m处管柱受到封隔器的约 束作用，加速度一直保持为零；同一时刻，从0 m变化到20 m，振动加速度逐渐增大，在管柱底端加速度达到最大值。在同一位置，加速度随时间周期性变化，越靠近管柱底端，幅值越大。同样的，Sofrygina等只是给出了位移随时间的变化关系曲线，据此可以推算出管柱最大加速度，采用同样的折算方法，本文与Sofrygina等研究中的管柱加速度相差7.8%。

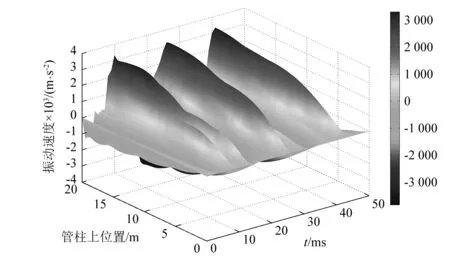
图6 管柱振动加速度随时间变化曲面Fig. 6 The vibration acceleration of pipe string with time changing surface

图7和图8分别为管柱自由端与固定端速度和加速度随时间变化曲线。由图可知，固定端受到封隔器的限制作用，其速度、加速度均为零；自由端的速度、加速度均随时间按周期15 ms变化。45 ms时，自由端速度达到最大值5.45 m/s；10 ms时，加速度达到最大值2.85 km/s2；速度、加速度幅值均随时间逐渐减小。

图7 自由端与固定端速度Fig.7 Velocity of constraint end and free end

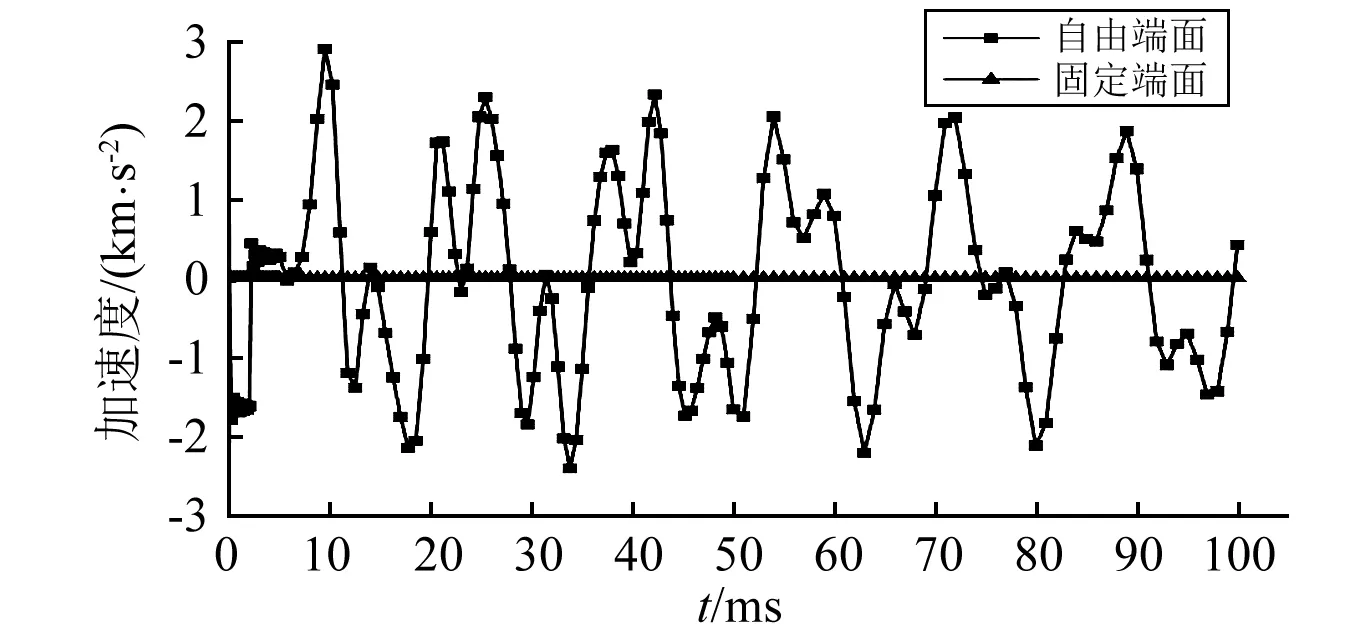
图8 自由端与固定端加速度Fig.8 Acceleration of constraint end and free end

4.5 射孔段管柱等效应力分析

冲击载荷作用于管柱后以弹性应力波的形式沿管柱传播，引起管柱的应力变化。如图9(a)所示，4 ms时，应力波传到管柱约束端；如图8(b)所示，23.6 ms时，等效应力达到最大值305.5 MPa，管柱截面上的应力分布并不均匀，等效应力沿径向逐渐增大，在管柱外表面达到最大值。

图10为管柱自由端和固定端最大等效应力随时间变化曲线。自由端等效应力曲线与冲击载荷曲线趋势相同，数值差别不大。固定端最大等效应力远大于自由端，按周期15 ms变化，幅度逐渐减小。4 ms以内，固定端最大等效应力由自重产生，变化不大；4 ms时应力波传至此处，等效应力突然增大，23.6 ms达到最大值305.5 MPa。与本文相关的权威文献[10-13]和文献[25-26]给出了射孔液的压力脉动规律，但是并未给出管柱各截面的应力变化规律，所以本文给出的应力变化规律可通过井下实测来获取数据，验证准确性，作为本文后续研究的重点。

图9 t=4 ms和t=23.6 ms时约束端von-Mises应力云图Fig.9 Von-Mises stress of the constraint end at the time of 4 ms and 23.6 ms

图10 自由端与固定端最大等效应力Fig.10 Maximum von-Mises stress of constraint end and free end

4.6 射孔段管柱应力波传播规律分析

如图11所示，为搞清管柱内应力波的传播规律，分析了0.01 ms，1 ms，2 ms，3 ms和4 ms时管柱最大等效应力的轴向分布情况。初始时刻，管柱只承受自重，等效应力较小，1 ms，2 ms，3 ms和4 ms时，应力波传到14 m，9 m，4 m和0 m(封隔器)处，据此可估算应力波在管柱内的传播速度约4 930 m/s，与前面分析的理论计算值5 123 m/s较接近。

5 装药质量和密度及射孔段长度的影响分析

以真实L101井为例，考察射孔弹装药密度、装药质量和射孔段长度对管柱和封隔器处的应状态的影响。射孔段油管采用Ф73×7.82 mmP110级油管，油管外径73 mm，油管内径57.36 mm。射孔段套管外径127 mm，内径102.72 mm。L101井的射孔段深度为5 945～5 968 m射孔段长度23 m，距离封隔器距离为41.5 m。采用了DP36HMX25-6型射孔弹；单发装药量25 g；装药密度1.69 g/cm3；射孔参数为89枪、102弹、相位角：60°、孔密：16孔/m。

图11 不同时刻管柱最大等效应力轴向分布曲线Fig.11 Curve of maximum von-Mises stress along the string at different time

5.1 装药密度对管柱强度安全性影响分析

其他参数保持不变，改变射孔弹装药密度，应用理论算法，分析装药密度对管柱强度安全性的影响规律。相关的计算结果如图12所示。可以看出，装药密度增加，封隔器处峰值压力和油管峰值应力增加，在射孔弹装药密度超过1.9 g/m3以后，封隔器处峰值压力和油管峰值应力增幅变缓，装药密度影响变小。

图12 装药密度影响分析曲线图Fig.12 Diagram of influence analysis of charge density

5.2 装药量对管柱强度安全性影响分析

其余参数不变，分析装药量改变对管柱强度安全性的影响规律。相关的计算结果如图13所示。可以看出，装药密度增加，封隔器处峰值压力和油管峰值应力增加，射孔弹装药量超过40 g以后，封隔器处峰值压力和油管峰值应力增幅变缓，装药量影响变小。

图13 装药量影响关系曲线图Fig.13 Influence relation diagram of loading capacity

5.3 射孔段长度对管柱强度安全性影响分析

其他参数保持不变，分析射孔段长度对管柱强度安全性的影响规律。相关的计算结果如图14所示。可以看出，射孔段长度从15 m增加到27 m，封隔器处峰值压力由299.6 MPa增加到335.4 MPa，增幅11.9%。油管峰值应力由745.1 MPa增加到790.6 MPa，增幅6.1%，增幅不大。

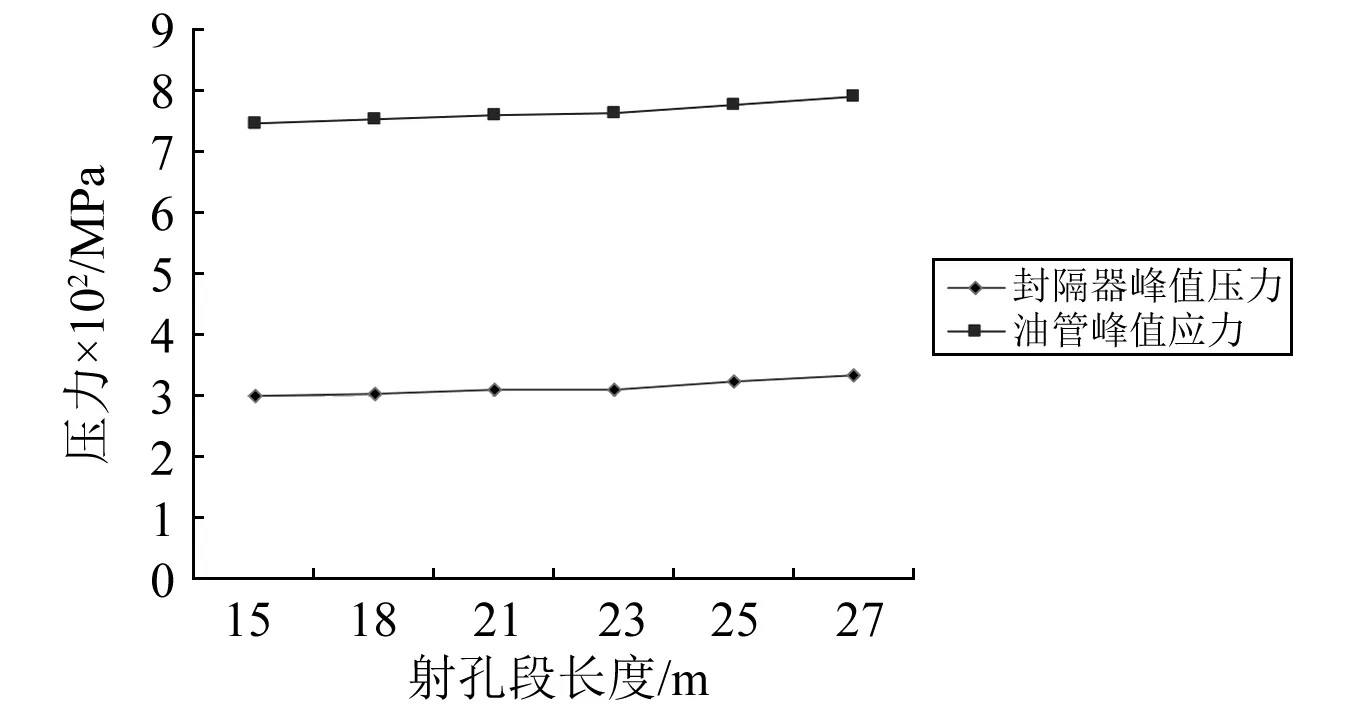
图14 射孔段长度影响关系曲线图Fig.14 Effect of the length of the perforation section

6 结 论

分析了管柱的动力响应规律，得到以下结论。

(1)应用振动力学悬臂梁理论，考虑管柱自重及轴向冲击载荷作用，建立管柱动力学模型，导出管柱纵向振动微分方程，应用分离变量法求解，得到管柱振动固有频率、主振型及位移动力响应表达式。

(2)管柱固有频率有限元和解析解相近，平均相对差4.18%，不超过5%，说明用有限元瞬态动力响应方法分析射孔段管柱动力响应，满足精度要求。

(3)位移、速度、加速度的变化幅值与文献[10-13]和文献[25-26]给出的变化幅值相差不超过10%，说明本文分析方法具有一定的适用性。

本文首次给出了冲击载荷作用下射孔段管柱不同时刻的各个截面的应力及其变化规律，现有文献均未给出。但是，包括管柱位移、速度、加速度、射孔液压力脉动和管柱应力需要通过井下实测的方式来获取实际参数。目前作者团队正在研制射孔管柱震动井下测试器，以验证本文算法。

考虑作为固壁约束的套管、弹性约束的射孔段管柱、射孔液、发生爆炸的射孔弹炸药及发生固液相变的药型罩之间的流固耦合，模拟爆轰、相变、大变形过程中的管柱位移、速度、加速度、射孔液压力脉动和管柱应力变化规律，将是有意义的尝试。