水电站机组-厂房结构突增负荷过渡过程振动特性研究

吴嵌嵌， 张雷克， 马震岳， 王雪妮

(1.三江学院 土木工程学院，南京 210012； 2.太原理工大学 水利科学与工程学院，太原 030024； 3.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116023；4.大连理工大学 建设工程学部水利工程学院，辽宁 大连 116023)

水轮发电机组是水电站实现经济效益和社会效益的核心设备及有效载体，厂房则是机组的重要支撑结构，同时也是运行人员进行生产活动的场所。水电机组及其支承结构的主要研究内容之一是其在水力、机械及电磁等振源作用下的振动特性讨论，研究旨在实现水电站机组和厂房结构稳定、高效及可靠的运行，且经数十年发展，相关成果已颇为丰硕[1-5]。尽管如此，当前研究存在的问题仍不能被忽视：①核心水力振源之一，即尾水管涡带压力脉动在系统动态特性分析中鲜有被提及；②研究内容主要关注系统的稳态振动响应情况，缺乏对其在过渡工况下的振动特性讨论[6-7]。

一方面，尾水管涡带压力脉动是引起水电机组及厂房结构振动最为主要的振源之一。受惠于计算机技术的迅猛发展，以计算流体动力学(Computational Fluid Dynamics，CFD)为代表的数值模拟手段在一定程度上实现了对脉动压力的预测。但受制于流体运动、边界条件和物性参数能否准确定义，由CFD带来的计算结果距工程实际应用尚存在一定距离[8]。更为重要的是，相比于机械和电磁等具有明确物理意义的公式，当前尚缺少关于尾水管涡带压力脉动的适宜数学表述。另一方面，水电站在电力系统中主要承担调峰、调频及调相等任务，诸如开机、关机、增负荷及减负荷等瞬态过程极为常见且不可避免。已有水电站振动实测结果显示，过渡过程虽然持续时间短暂，但机组和厂房在该瞬态过程下的振动响应数值可达其在稳态条件下的数倍[9]。此外，发生在岩滩、二滩和俄罗斯萨扬舒申斯克水电站等工程振动实例均表明，水电站机组和厂房结构出现的剧烈振动及由此带来的事故多发生于过渡过程之中，且多与尾水管压力脉动相关。因此，构建由尾水管涡带引发的核心水力振源数学模型，并将其引入机组-厂房结构开展瞬态振动分析，将有助于深入地了解机组与厂房在水力发电系统瞬态运行情况下的振动规律，从而对其出现的各种振动状况做出准确判断。

鉴于此，本文结合尾水管涡带在不同工况下的形成规律，从流体动力学理论出发，提出了一种适用于过渡过程分析的尾水管涡带压力脉动模型。在已有水力发电系统水-机-电-结构耦联模型基础上，将系统突增负荷这一典型过渡工况与机组-厂房结构振动结合，主要讨论系统在突增10%负荷小波动过渡过程中机组及厂房结构的动力特性，通过与之在稳态运行条件下的振动响应进行比对，明确机组-厂房结构在瞬态工况下的振动响应机制，从而为水电站水力发电机组、厂房等机械及土建结构在非稳态运行条件下的稳定性分析提供有益借鉴。

1 尾水管涡带压力脉动模型的构建

混流式水轮机转轮叶片固定，只有在设计最优工况下水流才沿叶片骨线方向无漩涡法向出流。而在偏离最优工况时，受水轮机出流旋转分量聚集的影响，转轮出口处会产生偏心涡带，进而产生尾水管压力脉动，该振源是诱发厂房和机组产生振动的主要因素。尾水管涡带在不同工况下的形成规律如图1所示[10]。因机组在55%～65%负荷区间水轮机转轮出口处涡带引起的压力脉动巨大[11]，有可能对机组及厂房振动造成非常不利的影响，故本文选取该范围作为水电站突增负荷过渡过程的模拟区间，进而讨论在该过程中机组及厂房结构的振动响应规律。

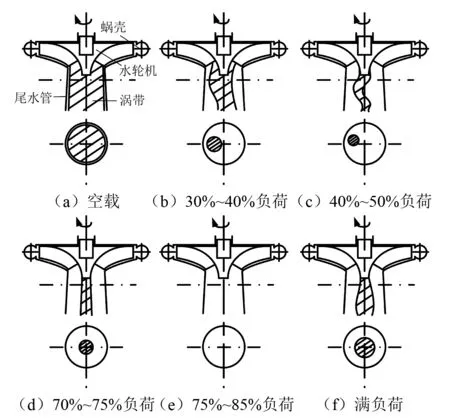
图1 尾水管偏心涡带随负荷变化规律Fig.1 Variation law of vortex shape

由于目前尚无一种较为成熟的数值方法来确定尾水管压力脉动对转轮振动的影响，无法有效地模拟其在转轮上所形成的水力不平衡力随时间的变化规律，故本文只考虑了作用在尾水管结构上的脉动压力荷载，忽略由尾水管入口处脉动压力对转轮体的影响，在水轮机转轮部分只引入机械偏心力和水密封力。为了模拟部分负荷工况下尾水管进口处的低频压力脉动，根据转轮出口环量和出口处速度三角形等关系[12]，首先推导出低频压力脉动fv的频率表达式，然后根据文献[13]所述求出压力脉动幅值P，利用这两个关键参数来模拟突增负荷时的压力脉动。

假设转轮出口处和和尾水管入口处位于同一位置，螺旋形涡带在尾水管中的旋转频率，即压力脉动的频率在整个尾水管各处相同。涡带在尾水管中的摆动频率，与其水流在尾水管进口处环量的大小有关。在此认为转轮的出口环量与尾水管进口环量相等，其表达式为

Γ=2πr2Vu2=2πraVua

(1)

式中：r2为转轮出口下环半径；ra为叶片出水边中点处半径；Vu2为转轮出口处绝对速度的圆周分量；Vua为叶片出水边中点处的圆周速度，如图2所示。

图2 水轮机转轮出口速度分量示意图Fig. 2 Schematic of velocity components at water turbine outlet

根据水轮机转轮的速度三角形可知转轮出口处流速为

Vu2=kV2-Vm2ctgβ2

(2)

式中:k为修正系数；V2为转轮出口水流的绝对速度；β2为叶片出水边的安放角；Vm2为转轮出口的轴向分量。将V2=2πr2n/60(n为转轮转速)和Vm2=Q/F(Q和F分别为水轮机流量及转轮出口过水断面面积)代入式(2)可得

(3)

尾水管进口处涡带旋转频率由定义可知

(4)

该涡带是一个旋转的流体涡旋，直径时变且以频率fv旋转造成尾水管内速度场周期变化。当涡带位于尾水管某一侧时该侧的速度增高、压力降低，而另一侧则是速度降低、压力升高，从而在尾水管内形成低频压力脉动。

对于该压力脉动的大小，由刘小兵研究中所述可以得到其表达式为

(5)

式中：ev为涡带偏心距，一般由实验确定；ρ为水体密度。

对于尾水涡带偏心距而言，目前尚无一种确定其大小的适用理论方法。利用实验实测或基于CFD数值模拟是当前仅有的两种手段，且相关研究极为有限。为了便于建立涡带偏心距与负荷工况之间的关系，本文假设不同负荷下的涡带偏心距在图1所示的过程中是线性变化的，同时，根据文献[14]在偏离设计工况时涡带偏心距的实验观测结果，并结合Favrel等的研究利用CFD得到的在非设计工况下尾水管涡带偏心距数值模拟结果，可以发现尾水管最大涡带偏心距分别约为水轮机转轮标称直径的20%和17.1%。本文水轮机标称直径为410 cm，从更为不利的角度考虑压力脉动的影响，则相应的尾水管涡带最大偏心距为410 cm×20% = 0.82 m，根据线性化假设则有如下偏心距与负荷工况的关系

(6)

同时，从便于应用和简化计算的角度考虑，在此假设其压力脉动符合如下变化规律，即

FPFDF=Psin(2πfvt)

(7)

由上述推导可知，尾水管涡带压力脉动的变化主要受脉动幅值及频率影响，在突增负荷过程中，脉动的幅值和频率因工况变化而随时间变化，故尾水管涡带压力脉动在过渡过程具有时变性，如图3所示。

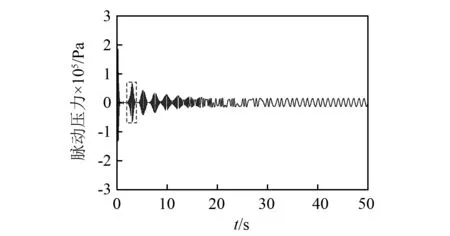
图3 尾水管涡带脉动压力模拟时域曲线Fig.3 Time history of pressure fluctuation of draft tube

需要说明的是，图3中0时刻意为突增负荷开始时刻，而非时间从0 s开始。在负荷工况由55%向65%迈进的过程中，水轮机功率随时间的变化如图5(c)所示。从图中可以发现，除个别时段水轮机功率波动大于70%以外，其余时刻该功率数值均处于50%～70%运行区间。在突增负荷初始，水轮机功率在55%～70%增长，由式(6)的假设可知，尾水管涡带偏心是由大变小的，其脉动压力幅值也在这个阶段由较大值逐渐减小；然后，水轮机功率继续增加，进入70%以上的区间，由式(6)的分段情况可知，当负荷在70%～85%区间变化时，假设的涡带偏心为0，相应的脉动压力幅值由式(5)可知为0；随后，水轮机功率下降至70%以下并达到一个峰值后又开始上升，在这个过程中，涡带偏心先增大后减小，所以脉动压力会出现如图3虚线框所示先增大后减小的变化规律，之后随着水轮机功率的波动出现相似的变化。当时间进一步延续，水轮机功率不断地向65%靠拢，脉动压力幅值也趋于稳定，直至进入稳态阶段。

需要强调的是，水力荷载特别是水力压力脉动影响因素错综复杂，对其发生机理和动态特性至今仍无完善解释和准确掌握。本文的侧重点在于机组-厂房结构在突增负荷下的动态特性分析，所构建的尾水管压力脉动模型是从理论分析角度出发，并仅从涡带偏心距变化这一主要因素入手，忽略了其他诸多影响条件，旨在通过增加核心水力振源使系统模型相对更为全面，故该水力激励模型是概化的，拟体现的是压力脉动的一般性变化规律，而非相对细化的实际模拟。建立能够反映尾水管涡带实际脉动压力脉动变化规律的模型已远超本文研究范畴，非现阶段作者所能实现。

2 数值计算模型

图4(a)为基于我国某实际水电站厂房设计图，利用Ansys软件所建立的三维机组-厂房结构有限元模型。其中，尾水管压力脉动作用于尾水管直管段(见图4(b))，机组轴系则简化为转子-轴承系统，如图4(c)所示。关于模型的具体构建过程详见吴嵌嵌等的研究。

图4 水电站机组-厂房结构模型Fig.4 Model of unit-plant structure

本文选用某型号为“HL180-LJ-410”的水轮机作为研究对象。增负荷过程自55%负荷工况开始，至65%负荷工况结束。期间，包括流量、转速和励磁电流等水、机、电参数将处于时变状态。而机组和厂房结构则主要受到尾水管压力脉动、机械偏心力、不平衡磁拉力(Unbalanced Magnetic Pull，UMP)和非线性密封力的影响。这些荷载因上述水、机、电参数的改变而变化，从而影响系统的动态特性。水轮机、调速器、发电机和转子-轴承模型数据如表1所示。

表1 模型参数表

3 数值模拟和结果分析

3.1 水、机、电参数在突增负荷过程中的变化规律

图5为包括机组转速、导叶开度、水轮机功率、电磁功率、端电压、励磁电流、流量及水头等水、机、电参数在系统由55%负荷突增至65%过程中的变化情况(注：如未特殊说明，图中各参数的变化均是从0 s突增负荷时开始)。

从图5(a)可以看出，在负荷突增情况下，转速在起始阶段会出现下降趋势，这是因水轮发电机组的电磁功率突增(见图5(d)的0 s时刻)、而水轮机功率保持不变所致(见图5(c)的0 s时刻)，相应地机组转速会在阻力矩(电磁力矩)的作用下降低。而后0～2 s内，为了应对阻力矩的增大，调速器会加大导叶开度(见图5(b))以增加水轮机力矩来对抗电磁力矩的增大。在该过程中，当机组转速下降到一定程度后，会在水力力矩增至与电磁力矩相等时停止下降。然而，由于惯性作用，水力力矩会继续增大，而转速则开始上升。此时，调速器会减小导叶开度以降低水轮机力矩，使之逐渐与电磁力矩平衡，在这个阶段转速会在额定转速范围内上下波动。最终，在25 s之后转速开始趋于稳定，如图5(a)所示。活动导叶开度与水轮机功率变化规律一致。在开始阶段，为了对抗电磁力矩的突增、防止转速降低，导叶开度迅速上升。随着导叶开度逐渐增大，水轮机功率也相应增加，在达到与电磁力矩的动态平衡点后再度下降。此后，导叶开度和水轮机功率在新的工况点附近波动，直至处于稳态工况。

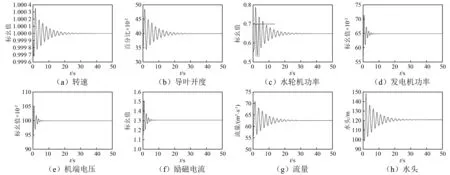
图5 水、机、电参数在过渡工况下的变化规律Fig.5 Variation of hydraulic, mechanical and electrical parameters

当电机负荷突增10%时，定子电流会突然增加，而发电机的电磁功率在当前时刻点无法激增(见图5(d))，所以导致发电机端电压在这一时刻突然降低至某个较低值，进而引起励磁电流突降。此时，为了适应负荷的增加，励磁调节会使励磁电流在短时间内快速加大，同时引起端电压的升高，以使电磁功率扩大来实现负荷的提升。在励磁调节的作用下，励磁电流迅速稳定在新工况点，发电机机端电压经过短暂的波动后恢复至额定电压值。电磁功率随机端电压的重新稳定和励磁电流的增加，最终也稳定在65%负荷处，使电机的输出满足负荷的要求。如图5(g)所示，水轮机流量变化是随着活动导叶的变化而变化的，两者规律相似。当流量增大时，会导致水头降低，而当流量逐渐稳定时，水头也会趋于稳定，如图5(h)所示。

尽管在起始时间及变化范围上存在一些差异，但上述各参数在水-机-电耦联突增负荷过渡工况下的变化规律与文献[15]中的水、机、电参数变化规律相似。因此，本文所建立的模型能够反映在该非稳态运行条件下的系统参数变化特性，可为后续开展相关荷载变化规律研究和结构动力特性分析提供可靠的保证。

3.2 机组各导轴承在突增负荷过程中的振动变化规律

为了更好地反映和分析瞬态过程下机组-厂房结构的动态特性，本文将整个增负荷过程按照水力波动和电磁波动规律分为四个阶段，即阶段Ⅰ：0～10 s；阶段Ⅱ：10～20 s；阶段Ⅲ：20～30 s；阶段Ⅳ：30～50 s。其中，0～30 s的波动阶段即为突增10%负荷后小波动变化过程，30～50 s的稳定阶段为65%部分负荷下运行的稳定工况。

在部分负荷工况下，机组及厂房结构所受的荷载主要包括机械偏心力、UMP(见图6)、转轮密封处的不平衡水力以及尾水管段压力脉动等。

图6 不平衡磁拉力变化规律Fig.6 Time history of UMP

图7～图12为水轮发电机组上、下和水导轴承在该过渡过程的轴心位移时程曲线及运动轨迹。图中A，B分别表示x向和y向的位移最大值点，其下标t和s则分别表示过渡工况和稳态工况(后续符号表示相同含义)。通过观察可以发现，在波动阶段I，由于系统负荷突增，电磁参数扰动和水力参数扰动共存，励磁电流在初始时刻突然降低然后又大幅升高(见图5(f))，同时流量也产生较大变化(见图5(h))，在转子处和水轮机密封处形成了极不稳定的电磁激励及水力激励，这些动荷载的波动对机组的运行稳定性造成了明显影响，不但各导轴承的运行轨迹变得极不规律(见图7(a)、图8(a)、图9(a))，同时，如图10～图12所示，其振幅也出现了显著的增加。其中，上导轴承在x和y方向的位移最大值分别为4.35×10-5m和4.61×10-5m；下导轴承各向最大值分别为5.49×10-5m和5.71×10-5m；对于水导轴承，其相应数值则分别为1.44×10-5m和1.27×10-5m。当过渡过程进入阶段II，随着电磁参数扰动的消失，励磁电流趋于稳定使不平衡磁拉力的变化逐渐平稳，同时流量变化幅度也在水轮机调速器的控制下慢慢减小，转轮密封处的水力荷载波动也随之降低，各导轴承轴心运动轨迹的不稳定性有所缓解。在波动阶段Ⅲ，稳定的励磁电流令不平衡磁拉力的幅值无显著改变，水轮机水密封处的不平衡力也因流量趋于平稳与水轮机轴心位移形成一种动态平衡关系，各导轴承轴心运动轨迹已基本处于稳态。在稳定阶段(30～50 s)，机组在调速器的作用下完成了过渡过程达到新的工况点并实现平稳运行。因流量、转速、励磁电流等参数不再出现激变，相应地各外激励荷载也处于稳定状态，如图7(d)、图8(d)、图9(d)所示，在稳定工况下上导轴承x和y方向最大位移分别为2.91×10-5m和2.61×10-5m，下导轴承各向则保持在3.66×10-5m和3.64×10-5m，对于水导轴承，其相应数值分别为1.22×10-5m和1.02×10-5m，各导轴承的轴心运动轨迹平稳，没有出现受到明显干扰的现象。

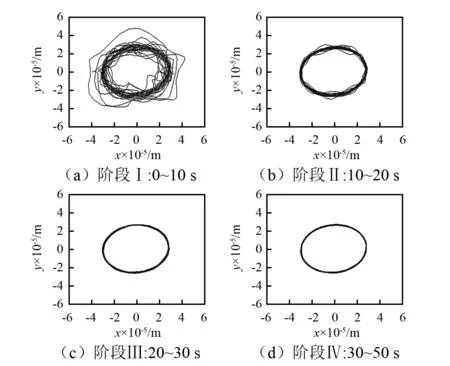
图7 上导轴承轴心运动轨迹Fig.7 Trajectories of upper guide bearing

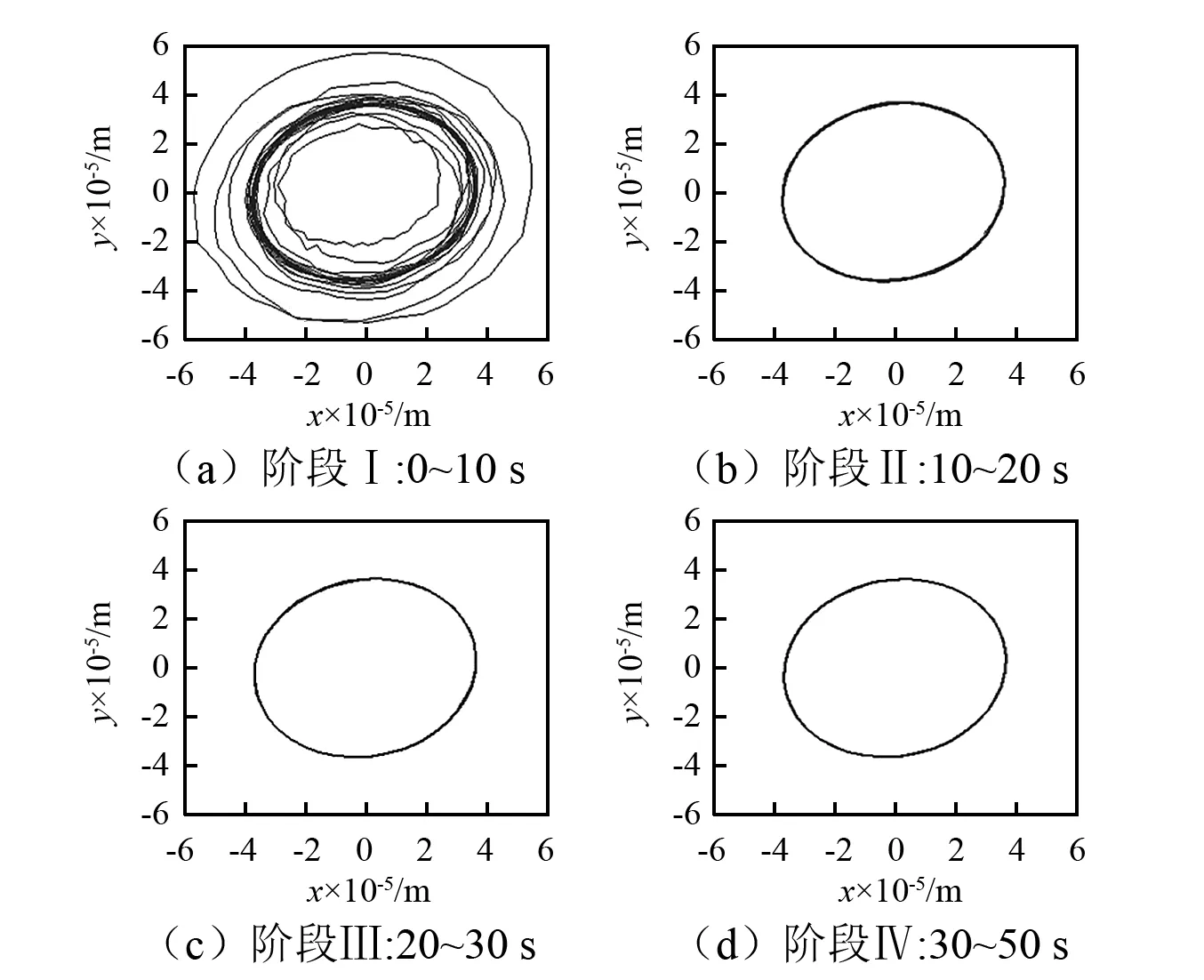
图8 下导轴承轴心运动轨迹Fig.8 Trajectories of lower guide bearing

图9 水导轴承轴心运动轨迹Fig.9 Trajectories of water guide bearing

通过比对过渡工况和稳定工况下各导轴承轴心运动轨迹可以发现，当系统处于过渡工况时，各导轴承轴心运动轨迹均出现明显的不稳定现象。这是因为已建水-机-电-结构动力耦联模型考虑了水、机、电参数的波动，所以在流量、励磁电流均出现大幅度改变的情况下，引起了作用在结构上的动荷载不稳定变化(例如，图3中的脉动压力变化和图6中不平衡磁力在0～30 s运行区间的波动)，进而造成在该过程中导轴承轴心运动轨迹的紊乱。其中，以上导轴承变化最为显著，下导轴承次之，最后为水导轴承。对于该现象可从如下两方面予以解释：首先，在不出现转轮密封引起的自激振动时，转轮处水密封力的数值远小于转子处的不平衡磁拉力，所以在突增负荷阶段，相比于密封力，不平衡磁拉力的作用更为显著，进而导致支承转子的上导轴承和下导轴承位移更容易受到该电磁激励的影响，致使其轴心运动轨迹更加不规则；其次，因尾水管压力脉动幅值增大并发生波动变化，相应地尾水管结构会产生较大的振动，该振动通过混凝土结构向上传导，后经由机墩到机架，最终通过机架等结构传递给机组并对其造成影响。通常情况下，对于布置立式机组的水电站厂房，机组的上导轴承支承在风罩顶部靠近发电机层楼板部位，下导轴承位于风罩底部的机墩部位，水导轴承则处在蜗壳混凝土结构附近，由此可见各导轴承对应的厂房结构部位整体刚度由上至下是依次增强的，所以上导轴承运动轨迹比下导轴承受到的影响更大。因此，从结构布置形式的角度而言，上、下、水导轴承在过渡工况下的运动不稳定现象依次减弱。除此之外，与稳态工况相比，各导轴承在该瞬态运行条件下的振幅增加也较为明显。通过计算可知，在此方面受过渡过程影响最大的是上导轴承y向，其振幅增加约为77%，最小的则是下导轴承x向，其增幅约为18%。当系统进入稳态运行区间，各导轴承轴心运动轨迹的表现则十分平稳。

图10 上导轴承振动时程曲线Fig.10 Time history of upper guide bearing

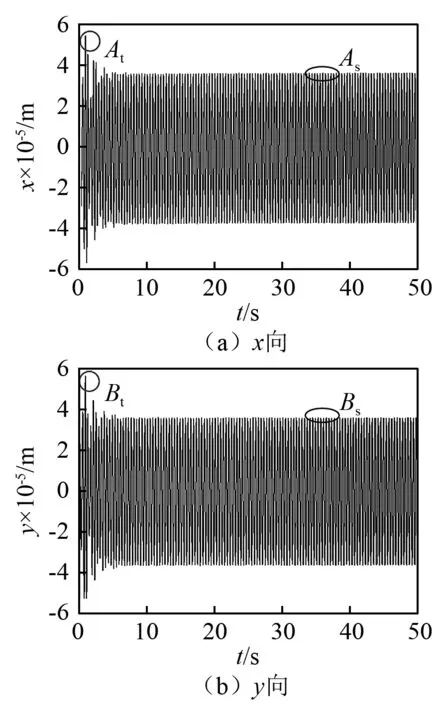
图11 下导轴承振动时程曲线Fig.11 Time history of lower guide bearing

图12 水导轴承振动时程曲线Fig.12 Time history of water guide bearing

然而，需要指出的是，虽然系统在离开过渡工况后，上、下及水导轴承的振动均呈现出动态稳定趋势，但由于压力脉动的持续存在以及不平衡磁拉力的作用，上导轴承的运动轨迹在所有导轴承中依旧最不规律，而水导轴承则相对表现最好。

3.3 厂房发电机层楼板在突增负荷过程中的振动变化规律

作为运行维护人员活动的主要场所，发电机层楼板层是水电站厂房结构中最为重要的组成部分之一，楼板的振动大小直接影响到现场人员的工作舒适程度，因此在厂房结构振动的研究中，常将发电机楼板层动力特性作为结构典型部分加以分析。

图13为发电机层楼板各向位移时程曲线。通过观察可知，在0～10 s运行区间，发电机层楼板各向振动均十分明显，其x方向，y方向和z方向最大位移分别达到了2.97×10-5m，3.97×10-5m和1.9×10-5m，如图中At,Bt,Ct所示。造成该现象的主要原因是：在该阶段电磁参数扰动和水力参数扰动共存，而由后者引起的尾水管处压力脉动变化也最为剧烈，故在各外激励的联合作用下厂房结构振动受到了非常显著的影响。同时，由于转子的上部支承结构与发电机层楼板位置接近，而由激增的不平衡磁拉力引起转子动力响应发生改变，其主要表现在转子振幅增大并不断变化，这种反应经由机架更容易传递到发电机层楼板，致使其振动幅值受到影响。当系统进入波动阶段Ⅱ，电磁参数扰动消失(见图6)，水力参数扰动及其诱发的脉动压力波动也逐渐减弱(见图3)，厂房结构各向振动开始逐步趋于平稳。在系统离开该运行区间后，由于水、机、电参数不再发生明显改变，楼板结构的振动也进入稳定状态，x方向，y方向和z方向的振幅分别稳定在2.01×10-5m，2.16×10-5m和3.16×10-6m。

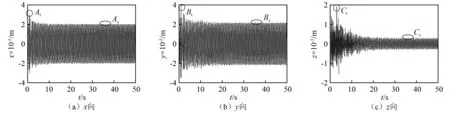
图13 发电机层楼板振动时程曲线Fig.13 Time history of generator floor

值得一提的是，厂房楼板各向振动以z方向在整个过程中受到的影响最大，同稳态工况相比其最大振动幅值增加高达502%。该增幅虽然巨大，然而，根据某电站振动实测结果显示，在过渡工况下厂房结构部分部位的振动有可能达到稳态工况的数倍乃至十余倍。相比于z方向，x方向和y方向的振幅增幅则要小很多，分别为48%和84%。之所以横向与竖向振动差异如此明显原因主要有三点：①相比于横向，楼板结构的竖向刚度明显要低，因此在同等外力作用下竖向变形及其振动会比水平方向更容易受到影响。所以，同x和y方向相比，在过渡过程下发电机层楼板z向会产生更为明显的位移变化；②过渡工况下，脉动压力荷载频率几乎从1 Hz(约为机组转频的四分之一)覆盖至30 Hz在内的所有低、中、高成分(见图14)，而发电机层楼板竖向基频为16.8 Hz，与压力脉动的中频存在重叠，势必因共振情况出现在发电机层楼板竖向激发出巨大的位移；③发电机层楼板水平方向基频为35.79 Hz，压力脉动在此频率附近的成分十分微弱，因此楼板水平方向在过渡过程中的振幅增加主要源于荷载的波动变化，而与共振无关，故其振幅增幅相对而言要小得多。

图14 尾水管涡带脉动压力频谱图Fig.14 Frequency spectrum of pressure fluctuation from draft tube vortex

当然，从图中不难发现，当系统进入稳态工况后，z方向位移明显要小于x方向和y方向位移，这是因为本文在计算过程中只考虑了结构的水平荷载，没有将竖向激励纳入建模范畴，而在稳态阶段荷载基本都属于低频激励，所以在过渡过程的水、机、电动荷载消失后系统仅存在横向方面的低频激励源，故发电机层楼板x方向和y方向的振动会更为明显，而z方向振动则因没有施加外部荷载而相对较小。

4 讨 论

综上所述，当机组与厂房结构处于过渡工况下运行时，相比于各导轴承，厂房结构特别是发电机层楼板结构更容易受过渡过程影响，其中以z方向表现最为突出。其主要原因在于厂房是对机组起支承作用的土建结构，当机组正常运行时，一方面，厂房因对机组运动的支承和约束而受其振动的影响；另一方面，厂房自身还要承受尾水管压力脉动这一核心水力荷载的作用。故当二者因负荷突增发生较大的波动时，厂房结构的振动势必受到干扰和影响。而楼板结构一直以来都是厂房整体结构中刚度相对较弱的部位(特别是其竖向部位)，一旦结构动荷载出现剧烈变化，产生与竖向自振频率相近的激励源，竖向振动必然会发生显著改变。相反，机组轴系因有导轴承和厂房结构的双重支承和保护，虽然在该过渡工况下各导轴承振幅均有不同程度的增加，但总体而言其所受的影响还是相对较小的。

由以上分析不难看出，若仅从稳态层面对机组-厂房结构的振动特性进行分析，而未将过渡过程的影响纳入研究体系，上述重要的振动现象和振动规律是很难甚至是根本无法通过构建稳态结构模型而体现出来的。因此，在已有水-机-电-结构耦联模型基础上，采用本文研究方法对机组-厂房结构开展在非稳态运行条件下的动力特性分析，将能够更为深入地了解机组与厂房结构在水力发电系统突增负荷过渡工况运行时的振动规律，并对其出现的各种振动状况做出准确判断，从而为机组-厂房结构运行的稳定性和安全性提供有益参考。

5 结 论

本文通过构建在不同工况下尾水管涡带压力脉动这一核心水力振源数学模型，在前期已有水-机-电-结构动力耦联模型的基础上，针对机组-厂房结构在突增10%负荷过渡工况下的振动特性进行了研究，主要结论如下：

(1)在突增负荷情况下，由于水、机、电参数变化导致结构外激励波动以及机组和厂房结构布置形式等原因，各导轴承轴心运动轨迹呈现明显的紊乱现象。其中，上导轴承所受影响最大，下导轴承次之，最后是水导轴承。同时，各导轴承的振幅均有不同程度的增大，其中最为显著的是上导轴承y方向，约为77%，最小的则是下导轴承x方向，约为18%。

(2)对于厂房发电机层楼板而言，在过渡工况下其各向振动位移均有非常明显的增加，其中，以竖向变化最为显著。由于结构布置及共振的原因，该向振幅可达其在稳态运行工况下的5倍，应引起足够的重视。