混合多稳态随机共振的故障信号检测

张 刚， 李红威

(1. 重庆邮电大学 通信与信息工程学院,重庆 400065；2. 重庆邮电大学 信号与信息处理重庆市重点实验室,重庆 400065)

强噪声背景下的微弱信号检测技术一直是信号检测与处理领域的研究热点，它在机械设备状态监测与故障诊断、应急救援和地震预测等领域应用广泛。微弱信号检测的本质为提高有用信号信噪比，因此检测技术主要集中为抑制含噪信号中的噪声提升信噪比，如滤波法、取样积分法、小波降噪、经验模态分解和变分模态分解[1]。但该类方法检测粒度大且易损坏有用信号，造成检测效果欠佳；而随机共振在检测微弱信号时利用噪声能量不损害待测信号成为目前研究的热点。

随机共振是Benzi等于1981年研究古气象变化时提出的，随后在物理、生物、电子等领域均得到证实[2]。应用到微弱信号检测中是将含噪信号通过非线性系统使周期驱动力和噪声驱动输出出现周期性的变化从而可将噪声的一部分能量转移给待测信号。随机共振产生的必要条件为势函数、噪声和信号的协同作用，大量学者围绕这三方面随机共振因素进行了深入研究，以一阶Langevin方程为基础的过阻尼随机共振模型分别有Woods-Saxon单稳态系统模型[3]、混合双稳系统模型[4]、三稳态模型[5]、并行阵列系统模型[6]；二阶方程较过阻尼具有近似滤波功能并且模型中含有可调的阻尼比增强了对噪声的适应能力，因此关于二阶方程的研究也在如火如荼的进行，比如基于逃逸率二阶方程下的广义调参随机共振[7]、二阶方程三稳态系统[8]。以上研究绝大数都是以理想化的高斯噪声为背景，与实际的噪声环境存在偏差，而α噪声是具有显著的拖尾特性和尖峰脉冲特性的非高斯噪声，能够更加接近于实际振动信号检测应用场景，因此α噪声作为背景噪声受到越来越多的关注，其中有α稳定噪声下时滞非对称单稳系统随机共振[9]、α噪声驱动的非对称双稳随机共振现象[10]、α噪声背景下的脉冲幅度调制(Pulse Amplitude Modulation, PAM)信号检测[11]。由于随机共振受到绝热近似理论的限制,因此在信号方面系统只能检测低频(f≪1 Hz)信号,而在实际工程中其信号频率远远大于1 Hz，极大的限制了随机共振的应用发展,学者们通过不同的信号预处理方法打破传统只能检测小信号的桎梏,其中包括移频变尺度随机共振[12]、二次采样的随机共振技术[13]、频率控制的自适应随机共振[14]、信号频谱重构的随机共振[15]等等。以上研究使得随机共振应用在实际工程信号处理中成为可能，其中最为典型是旋转机械系统故障检测，旋转机械在交通工具、航空发动机、发电机等广泛的工业应用中发挥着重要作用，其运行状态的好坏直接影响生产生活安全，但是由于复杂机械设备中存在大量强噪声使得轴承信号检测变得尤为困难，因此旋转机械的故障诊断问题极为突出。近年来涌现出大量研究:指数单稳随机共振系统的轴承故障信号检测[16]和变步长二阶随机共振系统的滚动轴承故障检测[17]、随机共振与经验模态分解结合的滚动轴承故障检测[18]等。目前为止，研究者发现Woods-Saxon模型具有平滑的底部，陡峭的势垒壁，能够保证粒子稳定运动使其达到较好输出[19]，而三稳态模型在微弱信号检测时有比其他稳态对噪声利用率高的特点；因此本文将混合双稳态随机共振系统与Woods-Saxon模型相结合，提出混合三稳态随机共振系统；然后利用自适应算法寻找混合型三稳随机共振系统最优参数组合，对α噪声背景下的仿真信号进行检测，证明其优越性；最后为了更加充分的聚集目标频率能量，将变分模态分解和混合三稳态随机共振进行组合并应用于实际轴承故障信号检测，仿真结果显示系统检测出的故障频率与实际计算特征频率相差无几，进一步验证了该系统的实用性，为该系统在实际工程的应用奠定了基础。

1 系统模型

1.1 Woods-Saxon单稳态

Woods-Saxon为对称的单稳态函数

(1)

式中：a为稳态壁陡峭程度；V为稳态深度；R为稳态宽度。由图1可知：稳态的两端收敛于x轴。由图1(a)可知:固定V,R单独调节a可以改变稳态壁的陡峭程度，并且随着a的减小稳态势阱壁逐渐变得陡峭。由图1(b)可知：固定R，a单独减小V，稳态深度减小，由图1(c)可知:固定V，a，调节R，稳态的宽度随着R的增大而增大并由其单独表征。因此势函数的形态由a,V,R联合控制，系统参数间的耦合性不高，可有效控制势函数的形态。

1.2 混合双稳态模型

在混合双稳态模型中势函数Um(x)是非线性对称双势阱，其势函数为

(2)

图2表示随着稳态参数b的增大，稳态壁逐渐变得陡峭且势垒高度减小，势函数形状由w型逐渐转变为u型；因此可知参数b将影响混合双稳态的稳态个数及稳态宽度，可有效控制混合型双稳态涵盖域及稳态间过渡。

图1 势函数随不同参数的变化Fig.1 Potential function for different parameters

图2 混合型双稳势函数随b的变化Fig.2 Hybrid bistable potential function for different b

1.3 组合模型

基于以上两种模型将Woods-Saxon单稳态模型与混合双稳态模型相结合提出一种混合型三稳态模型，势函数为

(3)

图3是混合型三稳态的势函数，其参考形态结构参数为(V,R,a,b)=(0.6,0.4,0.1,0.3)，由图3可知该函数为轴对称图形，两边势阱属于混合双稳态势阱而中间势阱属于Woods-Saxon,从而可知该系统既保留了Woods-Saxon的特性又增添了三稳态的优点。

图3 混合型三稳态势函数Fig.3 Hybrid tri-stable potential function for different value

通过调节系统参数V可知影响中间稳态深浅，参数a影响中间稳态壁的陡峭程度，参数R影响中间稳态区域窄宽，参数b影响整体势函数两边稳态壁的陡峭，由布朗粒子运动及势函数形态关系可知：布朗粒子从单或双势阱跃迁变为三势阱跃迁，极大的提高了噪声的利用率，而由这些参数引起的势阱与势垒的改变也直接影响粒子的跃迁难易程度。

1.4 系统模型

随机共振的三要素分别为：微弱驱动信号、噪声和非线性系统，代入布朗粒子运动方程中可以理解为布朗粒子在外部周期驱动力下通过非线性系统在势阱间的跃迁达到周期性，在不足以越过势垒的情况下，通过协调噪声的能量完成势阱间的跃迁,因此二阶三稳态布朗粒子运动方程为

(4)

其中传统的随机共振系统势函数及势阱力为[20]

(5)

而由式(3)可知混合三稳态势阱力为

(6)

由随机变量(x,y)的Fokker-Planck方程可知其概率密度函数

(7)

式中:k为阻尼比;s(t)为外部周期驱动力;ξ(t)为α噪声，其特征函数表达式为

(8)

由式(8)可知α值决定该分布的拖尾特性和脉冲特性。拖尾特性和脉冲特性在α变化时呈现互反性，α值由小变大时拖尾特性由强变弱，脉冲特性由弱变强。β∈[-1,1]为对称参数，确定分布的对称性称。参数σ∈[0,+∞)是尺度系数；μ∈(-∞,+∞)是位置参数，决定该分布的中心位置。由于α的特征指数越小，脉冲幅值就越大，振荡粒子跳跃的距离很可能趋向无穷大，针对这个问题，经过大量仿真验证对于混合三稳态数值仿真时对输出截断为5，双稳态为2。

1.5 α噪声的产生方法

α噪声的随机变量X通过Chambers-Mallows-Stuck方法产生[21]，当α≠1时

(9)

其中，

(10)

Dα,β,σ=σ[cos(arctan(βtan(πα/2)))]-1/α

(11)

当α=1时

(12)

式中：V为(-π/2,π/2)上的均匀分布；W为均值为1的指数分布，并且V和W相互独立。

1.6 二阶稳态方程的四阶Runge-Kutta法

(13)

1.7 系统参数优化调节

随机共振的产生依靠调节噪声强度、系统参数使其产生协同作用来增强淹没在噪声中的有用信号，但是在此过程中需要判定系统是否产生了随机共振，因此定量测度指标更加有助于实现和应用随机共振现象目前性能指标主要包括信噪比、信噪比增益、互相关系数、驻留时间等，而随机共振的主要特点就是将噪声的能量转化为有用信号的能量从而使有用信号实现非线性放大，最为直观的性能指标就是判定系统对输入信号进行非线性放大的程度。因此本文选取信噪比增益作为性能判定指标，其定义为输出信号功率谱中信号频率处的幅值与输出背景噪声之比同输入信号功率谱中信号频率处幅值与输入背景噪声之比的比值。该比值能较清晰的理解输出相比输入的受益程度，定义为

(14)

式中：snrout(f0)为输出信噪比；snrin(f0)为输入信噪比。由于实际应用场景中噪声的复杂程度，外界噪声源一定时其噪声强度固定，因此通过调节噪声强度实现随机共振较困难，目前的研究主要集中在系统结构参数调节实现共振，由“2.3”节可知，中间势阱主要依赖V，R，a控制，两边势阱的调节主要影响因子为b，耦合性较低，本文选取自适应参数调节随机共振，其具体步骤如下：

步骤1 初始化V，R，a及b,分别给定迭代步长和范围；

步骤2 更新V，R，a,在b的给定范围内搜索,比较信噪比增益,并记录最大信噪比增益时V,R,a,b;

步骤3 判断V,R,a是否超出搜索范围,若未超出则转到步骤2，若超出则停止更新转到步骤4；

步骤4 分别在步骤2记录的信噪比增益中调节k,找出并记录每次调节过程中的最大信噪比增益；

步骤5 比较步骤4记录的信噪比增益,找出最大的信噪比增益所在的V，R，a,b,k。

选取参数s(t)=0.8cos(0.2πt)，采样频率fs=5 Hz和采样点数N=10 000，α噪声参数：a=1.2，β=0和σ=1，μ=0，对于图4(a)选取系统参数a=3，R=1和b=0.02，k=0.1，图4(b)为固定系统参数R，b，k，而将V=5，图4(c)为固定系统参数V，b，k，令a=3，对于图4(d)为固定V，b，a，k，由图4(a)～图4(d)的各个系统参数在不同α下的信噪比增益均呈现“先增后减”的单峰现象，可证明该系统在α噪声下可产生随机共振现象且系统参数b的搜索范围小于V，a和R范围。由图4(e)，k为阻尼项在粒子运动过程中拥有阻碍粒子运动的功能，因此在实现随机共振时，当系统采用较高阻尼比时系统达到共振时所需的噪声能量更强，这一点可以从图中阻尼比由0.1增加到1时，信噪比增益曲线逐渐右移说明，因此在微弱信号检测时，可通过调节各个系统参数以及阻尼项使待测信号的信噪比增益达到最优值，从而检测出目标信号。

2 变分模态分解

变分模态分解(Variational Mode Decomposition，VMD)是一种自适应频率分解方法,每个模态由中心频率和带宽组成, 此过程可理解为迭代和搜寻变分问题的最优化,其中μk(t)为模态函数,具体求解步骤为

步骤1对于每一个μk(t)通过Hilbert得到其解析信号,利用exp(-jωkt)调制估计中心频率

(15)

步骤2每个模态都能紧密地围绕在各自中心脉冲频率ωk附近,ωk的带宽由以上解调信号的高斯平滑度来估算,则建立受约束的变分问题为

(16)

式中:f为原始信号;uk为模态函数;ωk为各个模态的中心频率。

式中:α为惩罚因子；λ为拉格朗日因子。

(18)

步骤5通过Parseval /Plancherel傅里叶等距变换将其转换到频域

(19)

通过ω=ω-ωk进行变量代换,然后将其转换为非负频率区间积分形式,最终求解的更新表达式为

(20)

(21)

算法流程如下:

步骤2n=n+1开始整个算法的循环；

步骤3 利用式(20)和式(21)更新uk和ωk,k=k+1,k∈(1,K),K为窄带模态函数分量个数；

步骤5 给定精度e>0,若满足判定表达式

则迭代终止,否则返回步骤2。

3 仿真信号分析

3.1 谐波振动信号

旋转机械广泛应用在交通工具、航空发动机、发电机等系统中，其运行时的安全可靠是减少经济损失、避免人身伤害的前提；因此若要保证机器的稳定，准确的健康监测与诊断系统对指示旋转机械可能发生的初期故障具有重要意义，通常旋转机械系统是通过产生的谐波振动信号获取机器的运行状态[22]，因此选取采样频率fs=5 000 Hz的谐波振动信号模型为

采样点数N=10 000，原始信号中其中各次谐波的幅度值d(m)m=1,2,3=[1,0.8,0.5]，信号基频f0=10 Hz，因此cos(4πf0t)和cos(6πf0t)是以f0为基频的二次谐波和三次谐波，其中:ξ(t)是噪声强度D=2的α噪声，参数设置为α=1.2，β=0，σ=1，μ=0。由图5(a)可知谐波振动信号完全被淹没在α噪声背景下，时域图只能观察到噪声特性。在将时域信号利用FFT变换后求其相应的功率谱图5(b)可知功率谱中特征频率无法识别，因此需要借助随机共振对信号进行非线性放大，但是由于随机共振受绝热近似理论的限制，而此时谐波振动信号的频率远大于1 Hz ，所以采用二次采样对谐波振动信号压缩等效为满足条件的低频信号，采样压缩比R=fs/fsr=1 000，二次采样频率为fsr=5 Hz。将淹没在α噪声中的谐波振动信号输入到经典双稳随机共振系统，其中系统参数和阻尼比(a,b,k)=(1,1,0.5)，从图5(c)可观察到其特征频率，但是在其高频还存在噪声频率而且干扰频率较多，因此采用式(13)对谐波振动含噪信号为输入的式(4)进行求解，利用自适应参数寻优系统参数组合为(V,R,a,b,k)=(0.5,1,1,0.01,0.3)。经过混合型三稳态随机共振系统后，图5(d)是显示谐波振动信号输出功率谱图，对比图5(b)、图5(c)相应功率谱可知随机共振系统可对含噪信号进行非线性放大凸显特征频率，对比图5(c)、图5(d)混合三稳态共振系统较经典双稳态系统在谐波振动信号特征频率处均有较大程度的提高，能够更好的协同噪声放大信号，最大程度的吸收高频噪声能量转化为低频有用信号能量，使特征频率更加明显，而且准确的检测出谐波振动信号，因此在α噪声背景下检测谐波振动信号混合三稳态系统优于经典双稳随机共振系统。

图5 经典双稳和混合三稳谐波信号检测Fig.5 The harmonic vibration signal detection of the classical bistable and hybrid tri-stable system

3.2 调幅信号

旋转机械完成旋转动作的主要部件为转子，转子常常会发生与静止件的碰撞摩擦，这时故障会引起振动信号的调制现象，因此有效识别和提取调幅振动信号调制特性对检测转子故障具有实际意义[23]。选取采样频率fs=20 000，采样点数N=10 000，调幅振动信号

s(t)=A(m)(1+cos(2πf1(t)))sin(2πmf0t)+ξ(t)

其初始幅度参数为A(m)m=1,2,3=[0.8,0.5,0.2]，其中调制频率f0=300 Hz，被调制频率f1=30 Hz，ξ(t)是噪声强度D=1.5的α噪声，噪声参数设置为α=1.2，β=0，σ=1，μ=0。图6(a)为原始调幅信号时域图形，在α噪声背景下的调幅信号功率谱图如图6(b)，调幅信号已经完全淹没在噪声下，由于0～10 kHz内均有频率点幅值，因此无法区别噪声和有用信号。利用二次采样对调幅振动信号压缩等效为满足条件的低频信号，采样压缩比R=fs/fsr=10 000，二次采样频率为fsr=2 Hz，将淹没在α噪声中的谐波振动信号送入经典双稳随机共振系统，其中系统参数和阻尼比(a,b,k)=(1,1,0.5)，由图6(c)可以看到在0～400 Hz内f0=300 Hz处功率谱幅值为579.1和f0+30 Hz处105.2,f0-30 Hz处126.4的谱峰值，400～800 Hz内只能观察到2f0=600 Hz处270.4的功率谱幅值，2f0±30 Hz周围存在着明显的干扰噪声频率，而在800～1 200 Hz内3f0=900 Hz及3f0±30 Hz完全被噪声所覆盖，由此可知经典双稳系统对调幅信号检测不佳，利用自适应参数寻优算法获得混合型三稳随机共振系统最优参数组合及阻尼比参数大小为(V,R,a,b,k)=(1,1,5,0.3,0.5)，图6(d)为经过混合三稳态系统的输出功率谱图,相比双稳态模型而言混合三稳态系统在800～1 200 Hz内能观察到3f0=900 Hz的谱峰值为1 042，对比图6(c)、图6(d)可知混合三稳态在转子故障引起的调幅振动信号检测中优点凸显，不仅检测信号的个数优于经典双稳，更是在待测信号功率谱幅值方面高于一个量级，因此混合三稳态系统扩展了信号的检测范围。

图6 经典双稳和混合三稳调幅信号检测Fig.6The amplitude modulated signal detection of the classical bistable and hybrid tri-stable system

3.3 周期衰减脉冲信号

轴承故障诊断中故障信号总是以冲击级数的形式出现[24]。因此选择含有α噪声的周期性单边衰减脉冲离散信号作为强噪声下的模拟轴承故障信号，其单周期衰减脉冲表达式为

s(t)=Aexp(-gt)sin(2πfnt)

采样频率为fs=20 000，固定频率为fn=1 200，故障频率为f0=200，幅度为A=0.8，衰减率g=600，采样点数N=10 000，图7(a)周期衰减脉冲信号时域图，在原始信号中加入α噪声，噪声强度D=0.2，参数设置为α=1.6和β=0，σ=1，μ=0。傅里叶变换后求得其功率谱如图7(b)中并没有观察到故障频率，最大幅值处为固定频率处。0～500 Hz内f0幅值过小，经过采样压缩比R=fs/fsr=10 000，二次采样频率fsr=2 Hz后送入经典双稳随机共振系统(a,b,k)=(1,1,0.5)，由图7(c)可以看到在0～1 200 Hz内处功率谱幅值为2.751，谱幅值较低且整个带宽内都存在噪声，噪声利用率较低；因此利用式(12)对含噪周期衰减脉冲信号为输入的式(4)进行求解，利用参数自适应寻优算法获得最优参数组合为(V,R,a,b,k)=(3,5,1.7,0.04,0.5)，图7(d)为经过混合三稳态系统的输出功率谱图，800～2 000 Hz处已无噪声存在，且能够检测出故障特征频率外的二倍频及三倍频，对比图7(c) 、图7(d)可知混合三稳态更适合于轴承故障的诊断，能够清晰、准确的提取出轴承故障的特征频率。

图7 经典双稳和混合三稳周期衰减脉冲信号检测Fig.7 The periodic unilateral attenuation impulse signal detection of the classical bistable and hybrid tri-stable system

4 深沟球轴承实验验证

滚动轴承故障信号具有非平稳性、微弱性，常常淹没在强大的背景噪声中难以发现和提取，极易对工程应用造成不可估量的损失，轴承故障常常以倍频形式存在，为验证变长模态分解与混合三稳随机共振组合系统在轴承故障信号检测的实用性。采用西储大学电气工程实验室型号为6205-2RS JEM SKF的深沟球轴承装置[25]。轴承转速1 797 r/min采样频率fs=12 kHz；表1滚动轴承主要计算参数，由式(22)计算外圈故障频率为107.3。

图8 6205-2RS JEM SKF实验与采集装置Fig.8 6205-2RS JEM SKF experimental equipment

表1 6205-2RS JEM SKF轴承参数

轴承故障信号频率计算

(22)

图9 故障信号的时域图和频域图Fig.9 The time domain and frequency of the fault signal

图10 加噪信号时频图Fig.10 The time domain and frequency of the noisy fault signal

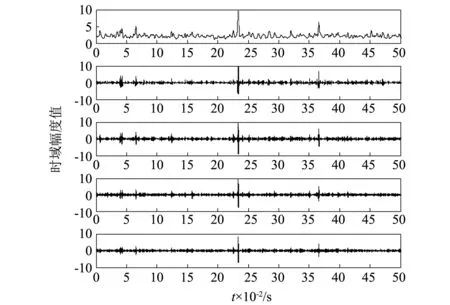
图11 变分模态分解时域图Fig.11 The time domain of the VMD

图12 变分模态分解功率谱图Fig.12 The frequency of the VMD

图13 重构信号时频图Fig.13 The time and frequency of the reconstructed signals

图14 组合系统输出时频图Fig.14 The time and frequency of combined system

5 结 论

本文将Woods-Saxon单稳态系统与混合双稳态系统组合成一种新型的三稳系统，称为混合型型三稳随机共振系统。该系统不仅保留了Woods-Saxon对于轴承信号检测的优良性，而且拥有三稳态对噪声充分利用的特点，文中以信噪比增益为衡量指标，利用自适应算法通过调节系统参数(V,R,a,b,k)实现随机共振的最佳输出，而且利用噪声的变化证明了混合三稳态信噪比增益符合随机共振的典型先增后减特性，针对α噪声背景的谐波振动信号、调幅信号、周期衰减脉冲信号进行检测，结果表明：混合三稳态系统在三者检测中均优于经典双稳态系统，能够检测出经典双稳态未检测出的待测信号。为了更好的将系统应用于实际，将变长模态分解与混合三稳态结合，能够实现更近一步的聚集目标频率能量,通过实际轴承信号验证，该系统在复杂噪声背景下不仅检测出轴承特征频率而且清晰显示其倍频，充分的证明了该系统在故障检测效果的良好性，因此本文为所提系统的应用提供了有意义的参考价值。