深水测试管柱测试过程中横向振动特性分析

孙巧雷，王高磊，靳祖文，孟文波，冯 定*，张 崇

（1.长江大学机械工程学院，荆州 434023；2.湖北省油气钻完井工具工程技术研究中心，荆州 434023；3.中海石油（中国）有限公司湛江分公司，湛江 5524057）

0 引 言

自2014年我国自营深水勘探的第一个重大油气田陵水17-2被发现以来，我国的深水作业技术逐步得到发展，深水海域的作业也进一步增多［1-2］。深水测试作业是深水油气田勘探开发的关键环节，为深水油气田的参数获取、储能评价、后期高效开采提供相关依据；深水测试管柱是安全高效完成测试作业的关键基础，为深水油气测试提供安全通道［3-4］。在深水测试作业过程中，测试管柱与隔水管组成“管中管”结构，在风浪流等海洋环境载荷的作用下，测试管柱与隔水管均会受到钻井平台的运动影响；同时，隔水管在海流作用下的横向变形使得其与测试管柱间存在接触碰撞；此外，由于内部气流与环空流体的影响，深水测试管柱的横向振动参数势必变得复杂，在极端载荷作用下易导致测试管柱的弯曲、碰撞、磨损等［5］。

在深水管柱领域，此前研究较多的是隔水管与柔性立管等［6-8］，而在深水测试管柱领域，近几年的研究才逐渐增多。唐海雄［9］、Liu［10］、何玉发［11］、杨志［12］等围绕测试管柱的温压场分布、管柱变形、管柱的优化等开展了研究，并提出了相关的计算模型；谢鑫［13］、刘秀全［14］、刘红兵［15］等基于构建的理论分析模型，应用有限元法，分别进行了波浪载荷作用下的管柱动力响应分析、测试管柱与隔水管间的接触特性及涡激振动分析。但目前有关测试管柱动力学相关的理论研究较少，基于此，笔者基于我国南海自营深水测试所使用的“管中管”结构特点，结合测试管柱的实际承载特性，应用Hamilton能量法，建立了深水测试管柱横向振动模型；应用数值仿真求解与编程的方法，对测试管柱的横向振动参数进行了求解，并研究了测试管柱悬挂力、水深、管柱壁厚及产量对测试管柱横向振动参数的影响，为深水测试作业安全控制提供了一定的理论依据。

1 深水测试管柱横向振动模型的建立

1.1 深水测试管柱简介

深水测试管柱主要由海水段与地层段的管柱两部分组成，其中地层段的管柱由悬挂器坐挂在泥线井口处，其可借鉴陆上管柱进行分析。深水段测试管柱由于位于隔水管内，其结构如图1所示，其主要组成包括测试油管、提升短节、扶正器、快速接头、储能器、承留阀、剪切短节、悬挂器、水下测试树等。测试管柱本身不受风浪流等环境载荷的直接作用，但在隔水管与平台以及内部测试流体的综合影响下，测试管柱的横向振动依然较复杂。

图1 深水段测试管柱结构简图Fig.1 Schematic diagram of structure test string in deepwater section

1.2 深水测试管柱横向振动模型建立

在建立深水测试管柱的力学模型时，需对其结构和运动做一定假设：①假设深水段测试管柱是匀质、各向同性的线弹性等截面圆管；②管柱微元的变形量及其变形角均为小量；③不考虑隔水管对测试管柱刚度的影响；④假设测试管柱与隔水管接触力稳定；⑤考虑实际扶正器的复杂性和实例井情况，本研究暂忽略扶正器的影响。在测试过程中，可认为初始状态下测试管柱与隔水管同心对中，取长度为ds的测试管柱微元，以泥线处管柱中心为原点，在假设单元为小变形量时，可认为ds=dz，管柱中点的倾角为∂x/∂z，管柱端面的力包括轴向力T、弯矩M和剪力N，内外流体及隔水管等对测试管柱微元的横向作用合力为Fx（z，t）。

根据Hamilton定理［16］，管柱微元的能量变化可表示为

式中：dUw为管柱微元的动能，为管柱微元的重量，x为管柱横向位移，t为时间；dUM为管柱微元弯矩产生的形变能，dUM=为管柱弹性模量，I为管柱惯性矩；dUT为管柱轴向力产生形变能，T为管柱轴向力；dUF为等效横向外载荷所做的功，dWF=Fo（z，t）xdz。

假设测试管柱振动是周期性的，且横向振动周期为τ，则长度为L的测试管柱在一个周期内总能量变化为

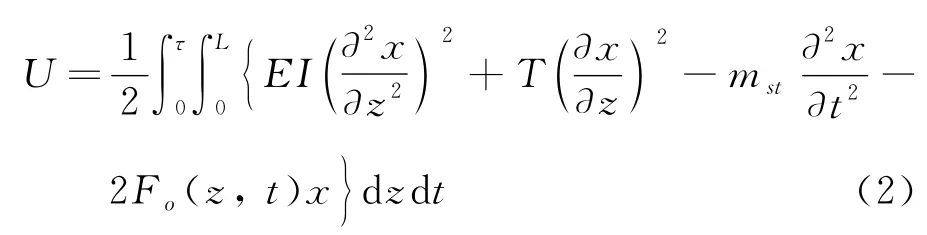
由式（2）可知，能量函数U是关于测试管柱横向振动曲线x（z，t）的泛函数。根据能量最低（稳态）原理，可能的横向振动曲线x（z，t）应使得U取极小值［17］，根据泛函数的变分相关理论，U取极小值的必要条件需满足欧拉公式，即

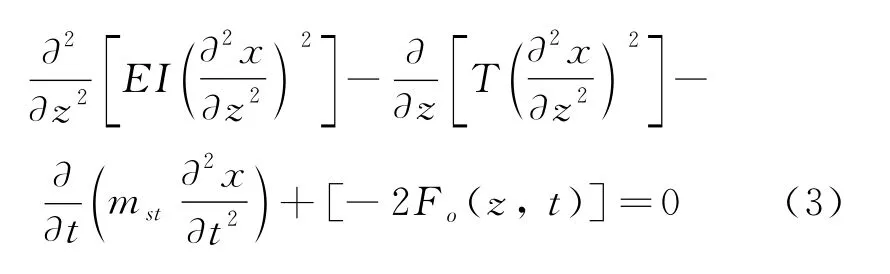
由式（3）可获得海上测试管柱横向振动的微分方程：

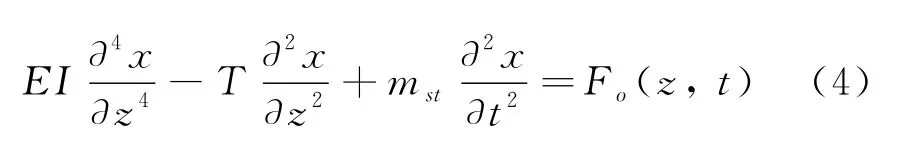
1.3 测试管柱横向载荷计算

在深水测试管柱作业过程中，测试管柱的横向载荷可表示为

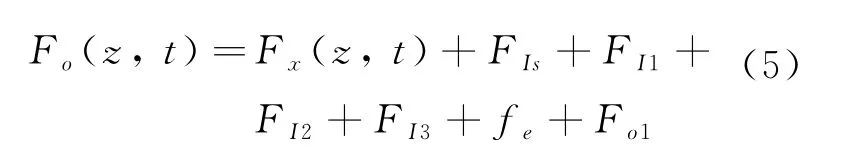
式中，FIs为管柱微元的惯性力，N；FI1、FI2、FI3分别为内部流体的牵连惯性力、相对惯性力和科式惯性力，N；fe为管柱内外壁与内外流体间的横向摩阻分量，N；Fo1为测试管柱外部流体的附连惯性力，N。

管柱微元的惯性力为

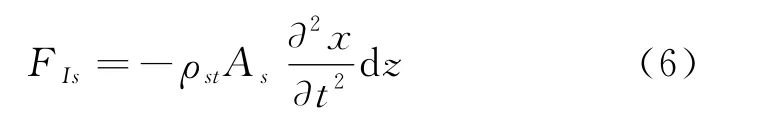
式中：ρst为测试管柱的密度，kg/m3；As为管柱微元的横截面面积，m2。

内部流体的惯性力可表示为

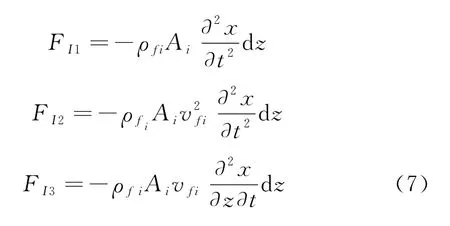
式中：ρfi为管柱内流体密度，kg/m3；Ai为管柱内部流道截面面积，m2。

在考虑内外流体流动时，假设流体流动方向均为向上，忽略压力瞬时波动的影响，fe计算公式为

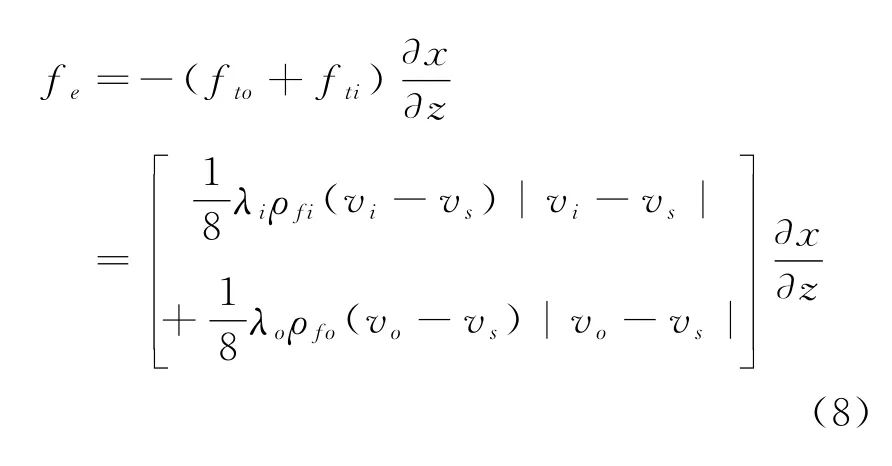
式中：fti、fto分别为管柱与其内外流体间的摩阻力，N；λi为内部流体与管柱间的摩阻系数；λo为环空流体与管柱间的摩阻系数；ρfo为环空流体密度，kg/m3；vi为内部流体流速，m/s；vo为环空流体流速，m/s；vs为管柱运动速度，m/s。

环空流体的附连惯性力Fo1可表示为

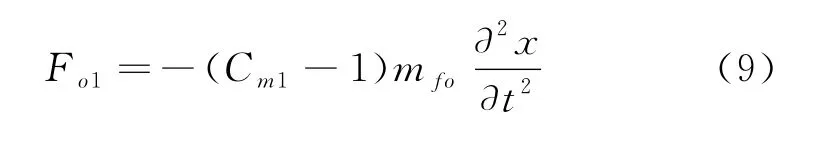
式中：Cm1为测试液附加质量系数，反映环空间隙及附加横向力的影响［17］，一般通过试验或应用经验公式求得；mfo为单位时间环空流体的质量流量，kg/m。

结合式（4）～式（9），令mfi=ρfi Ai，mst=ρst As，则深水测试管柱横向振动的控制方程可表示为

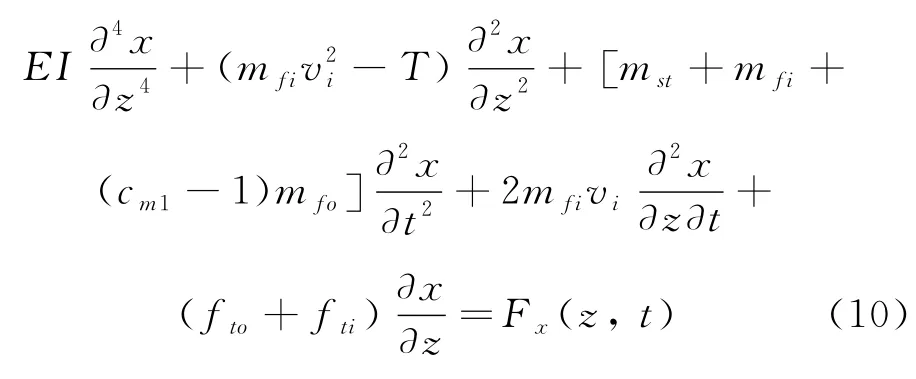
2 模型求解

2.1 控制方程的解

在深水测试作业产量测试过程中，测试管柱的环空流体为保温测试液，测试液的相态和流动一般变化较小，可忽略环空流体的影响；同时假设测试管柱横向动态位移函数为x（z，t），对x（z，t）进行分离：

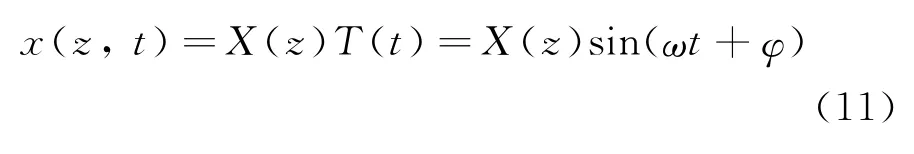
式中：X（z）为测试管柱主振型；sin（ωt+φ）为周期函数；ω为角频率；φ为相位差。

假设测试管柱横向振动为周期振动，隔水管与测试管柱间的接触力为周期性的，此时sin（ωt+φ）反映了隔水管对测试管柱周期性的参量值。在式（10）中忽略了小量的影响，同时取式（10）的齐次方程求解，此时获得产量稳定下的管柱横向振动齐次方程为

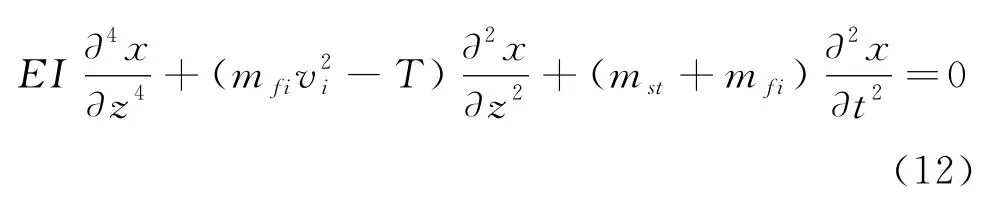
将式（11）代入式（12），令T（z）=mfiv2i-T、同时两侧同时除以EI·sin（ωt+φ），则

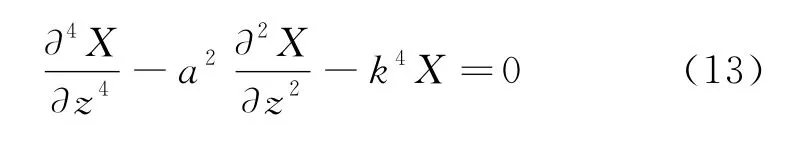
同时，根据深水测试管柱上下端的约束形式，可将其上下端认为固定铰链支座约束，即z=0时，时，X（L）=0，结合高等数学四阶齐次方程解的形式，式（13）的解可表示为

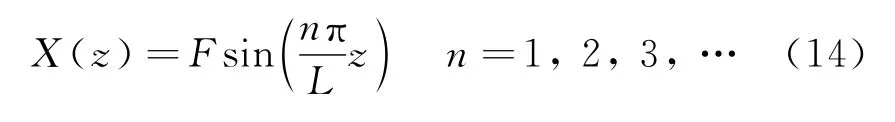
2.2 振型求解方法

基于傅里叶级数展开原理，测试管柱位移x（z，t）由不同振幅和频率的无穷个正弦波的形式进行叠加［18］，不考虑相位差φ的影响（φ=0），x（z，t）可表示为

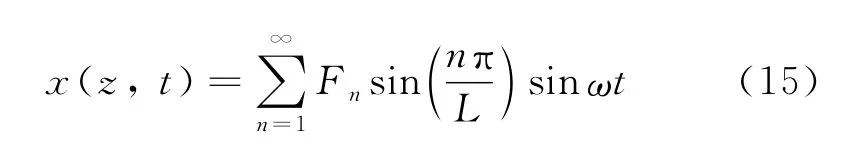
在计算测试管柱振幅时，在测试管柱单个周期的横向振动范围内，，则管柱的横向振动形式与横向载荷Fo（z，t）的非常数项相关，定义式（2）中Fo（z，t）x（z，t）有效积分项（非零积分项）为，此时将式（15）代入式（2），结合U取极小值的条件，则，此时有

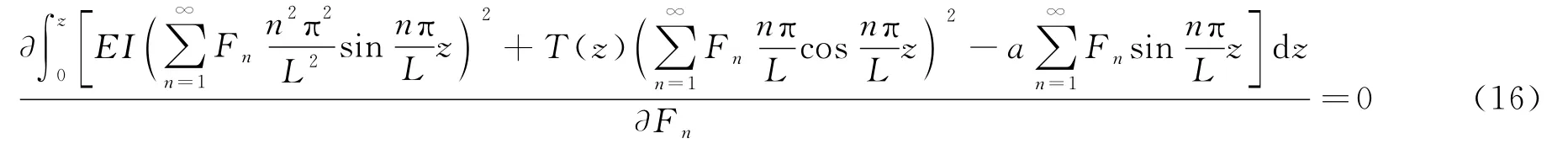
对于管柱的振动，考虑到振动的衰减与能量主要集中在其前几阶，本文选取了管柱的前6节振幅Fn进行求解，则振动模型最终的求解方程可转化为

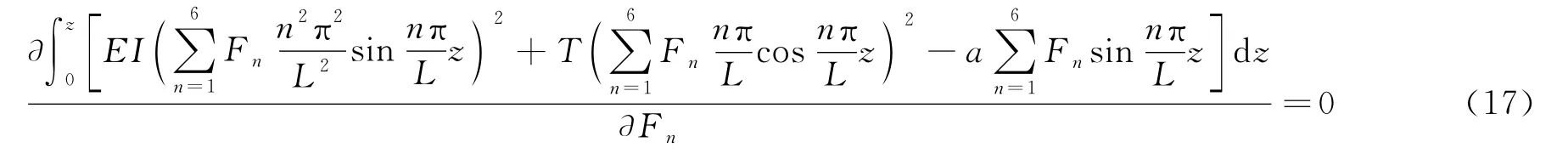
式（17）即为测试管柱前六阶振幅Fn的线性方程组，在系数EI、T（z）、m已知的情况下，可通过数值求解软件Matlab对Fn进行求解，随后将Fn的值代入测试管柱位移方程即可获得测试管柱的横向振动方程；对于测试管柱的横向振动频率，由于其受隔水管对测试管柱作用力的频率影响，因此，这里不对其进行讨论。

3 实例分析与应用

3.1 测试管柱相关参数

以我国南海已完成测试的某A井为例，该井水深975 m，测试管柱主体外径为114.3 mm，内径为85.85 mm，弹性模量E=206 GPa，大钩悬挂力为1 066 kN，环空流体密度为1 310 kg/m3，100万方测试 产 量 下T（z）=212 875+875z、m=50.252 kg/m［19-20］。此时，求得测试管柱的最大横向振幅如图2所示，此时管柱整体受拉，各阶振幅随阶数的增大而减小，管柱最大振动位移受前三阶振幅影响较大，与隔水管的振动规律相似［21］。

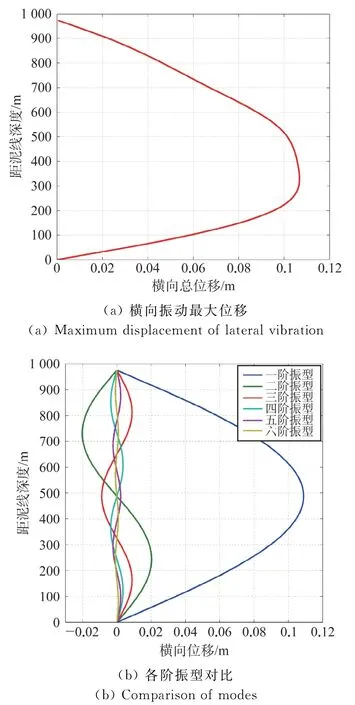
图2 测试管柱横向振型图Fig.2 Lateral vibration mode of test string

3.2 不同悬挂力对测试管柱横向位移的影响

测试过程中的悬挂力受海洋环境载荷以及海上钻井平台的影响较大，其可通过改变测试管柱配长、测试管柱与封隔器的相对位置进行适当调整，一般测试前需对大钩的悬挂力进行设计。针对悬挂力对测试管柱横向振动的影响，本节基于A井坐封后T0=1 066 kN的悬挂力，选取悬挂力范围为0.5T0～1.5T0分析悬挂力对深水测试管柱横向振动的影响。获得测试管柱的前六阶振幅如表1所示，最大横向位移如图3所示。

由表1和图3的相关结果可知：在悬挂力为0.5T0～0.8T0范围内，测试管柱的各阶振幅变化复杂，主要原因是此时测试管柱局部受压明显，测试管柱横向振动的振幅各阶值变化较大；而在0.8T0～1.5T0内，管柱整体受拉，测试管柱的最大位移以一阶振幅为主，最大横向位移随着悬挂力的增大而减小，但减小幅度逐步减小，最大位移点由靠近泥线处转换为逐渐靠近一阶最大位移的中点。因此，对于深水测试管柱而言，适当增大测试管柱的悬挂力能有效减小测试管柱的横向振动位移。

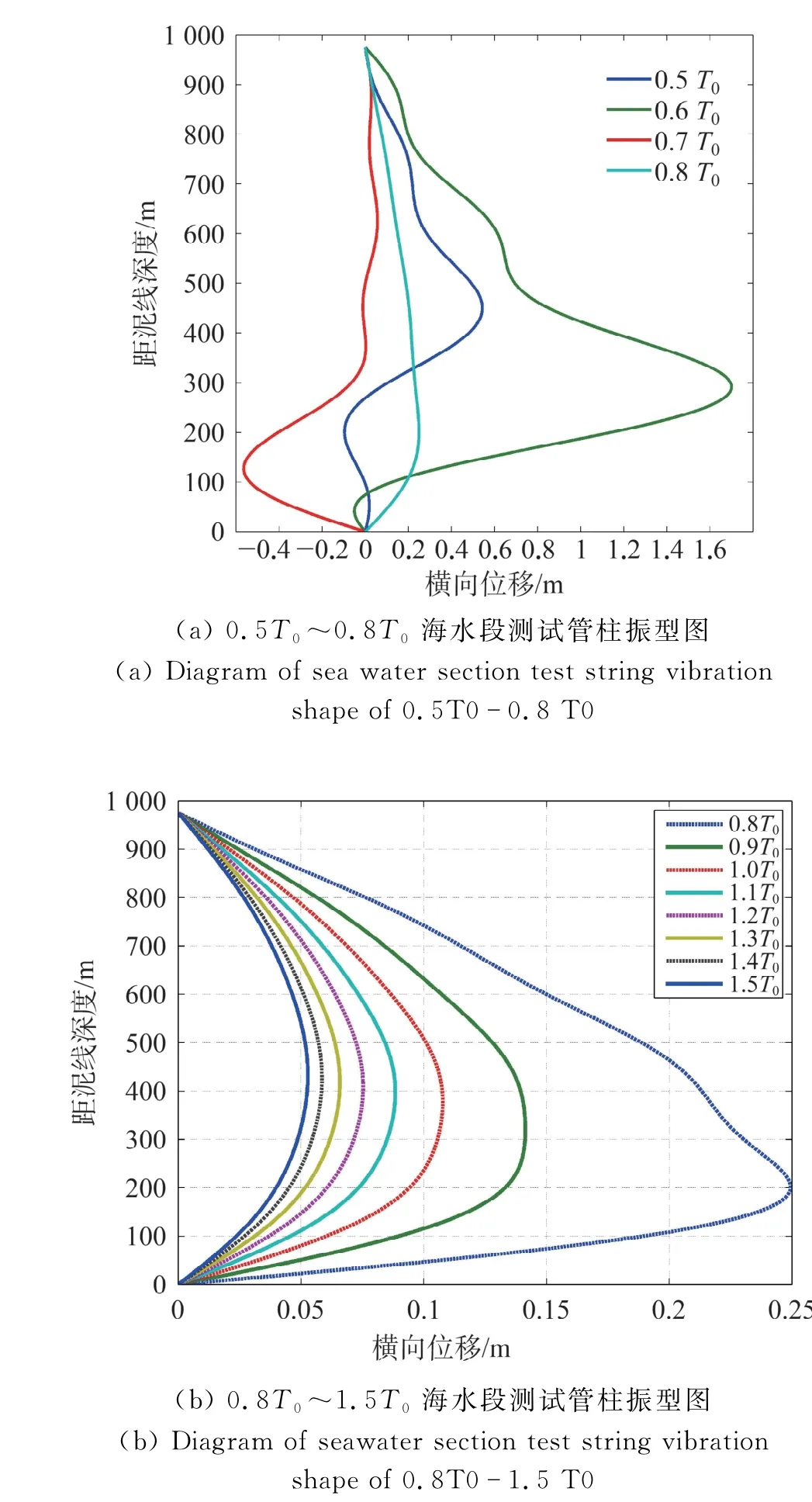
图3 不同悬挂力下的测试管柱最大横向振动位移Fig.3 Maximum lateral vibration displacement of test string under different suspension forces

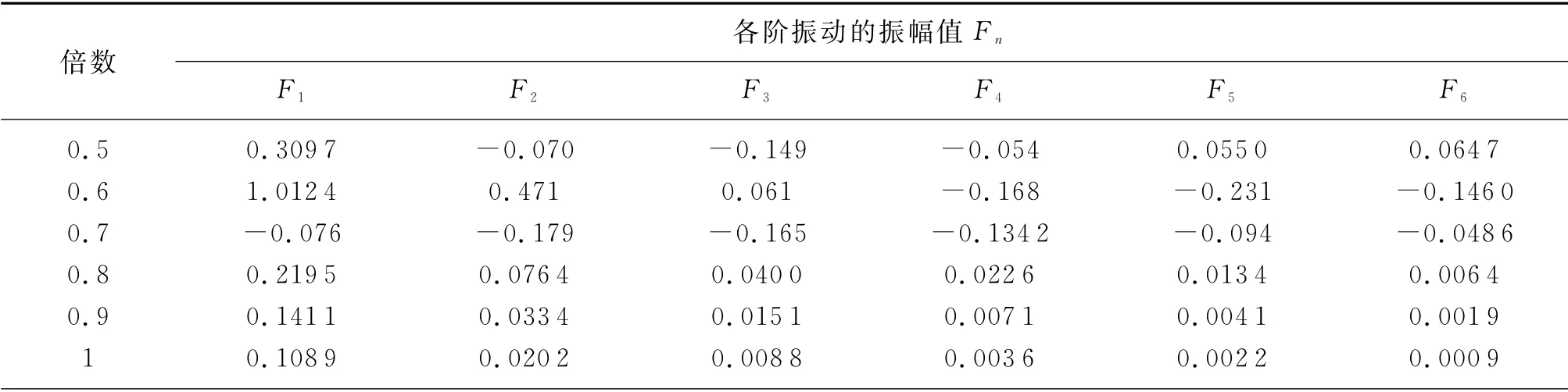
表1 不同悬挂力对应的前六阶振幅Fn值Tab.1 First six amplitude values corresponding to different suspension forces

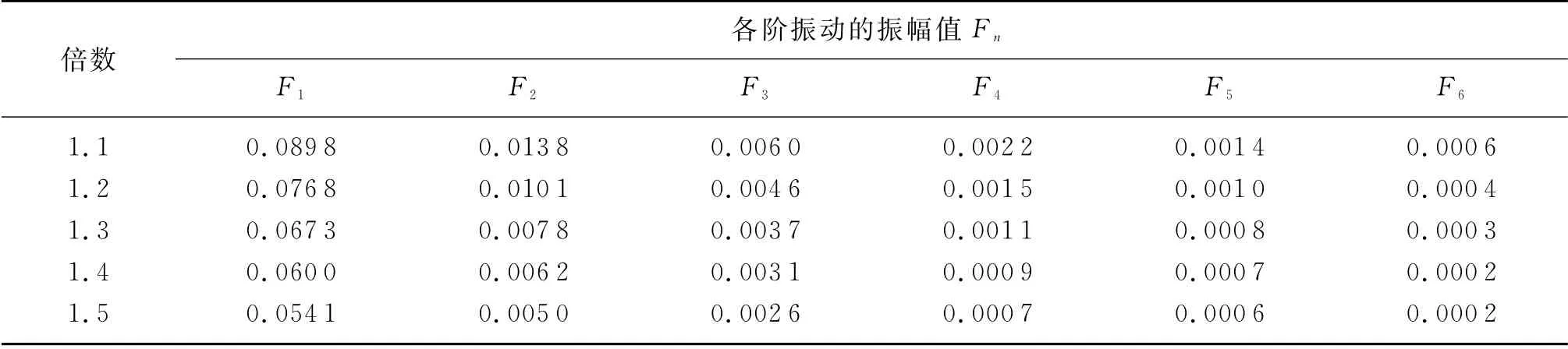
（续表）

3.3 水深对测试管柱横向位移的影响

随着我国在南海测试作业技术的提高与完善，我国自营深水测试作业的水深逐步增大，目前最大水深已超过1 800 m，在后续的规划中，测试水深将进一步增大。随着水深与井深的增大，测试管柱的横向振动特性也将改变，本文在A井设计的基础上，在水深增大的同时，按管柱浮重同比例增大测试管柱悬挂力。根据水深500 m、1 000 m、1 500 m、2 000 m、2 500 m、3 000 m时对应悬挂力的大小，得到了测试管柱横向振动的各阶振幅，如图4所示，此时测试管柱的各阶振幅随水深呈线性增长。而在悬挂力为1 066 kN时，测试管柱的各阶振幅如表2所示。

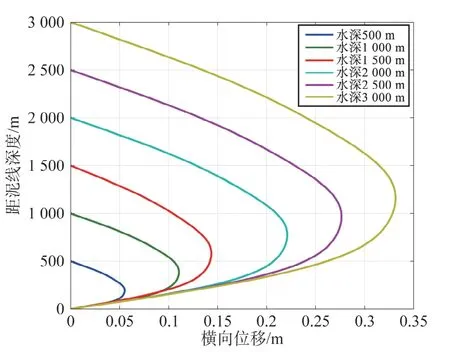
图4 悬挂力等比例变化下不同水深对应的最大横向振动位移Fig.4 Maximum lateral vibration displacement corresponding to different water depths in the proportional change of the suspension force

由图4和表2的相关结果可知：管柱悬挂力随水深增大对应增大，测试管柱最大横向振动随水深增大而增大，最大横向位移与水深似线性增加；悬挂力不变时，水深的增加使下部受压段长度增长，各阶振幅值无规律变化的同时，各阶振型变化较大。因此，当测试作业水深增大时，除需对应增加测试管柱的悬挂力外，还应考虑适当增大测试管柱与隔水管间的环空间隙，以减少隔水管与测试管柱接触与碰撞的可能性。

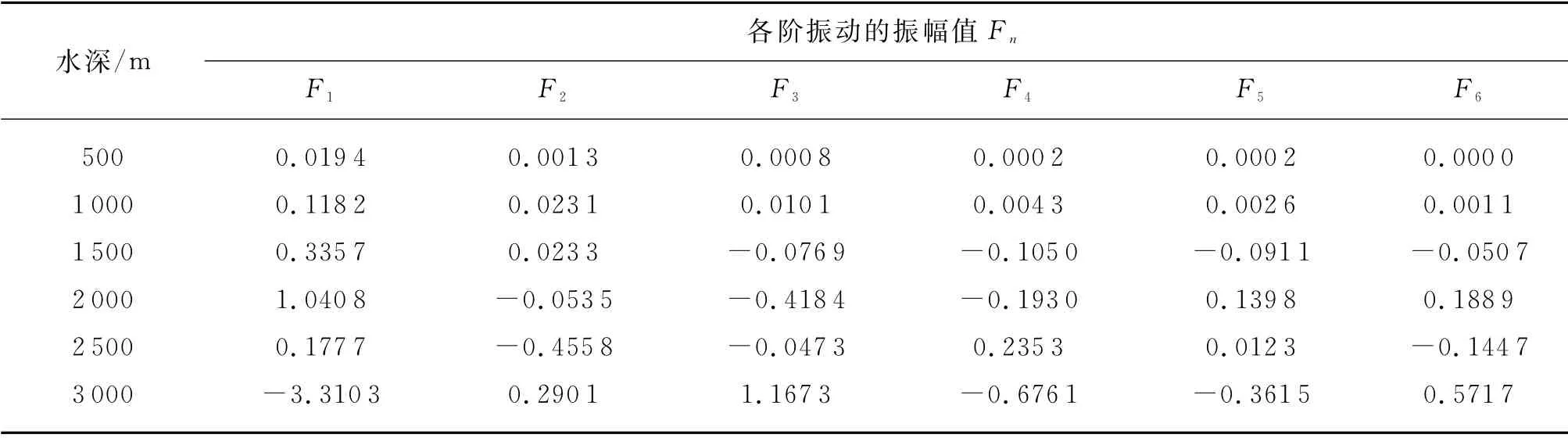
表2 悬挂力不变不同水深对应的前六阶振幅Fn值Tab.2 First six amplitude values corresponding to different water depths at a constant suspension force

3.4 管柱壁厚对测试管柱横向位移的影响

对于固定尺寸的测试管柱，即外径不变的测试管柱而言，合理选择壁厚也是减小管柱振动参数的关键。结合现场41/2′油管的尺寸系列，选取了现场常用壁厚分别为7 mm、8.55 mm、10.5 mm和14.225 mm的测试油管，进行产量相同时的测试管柱横向振动特性研究。通过计算其对应的温压场及其他相关数据，获得前六阶振幅，如表3所示，对应不同壁厚的最大横向振动振型如图5所示。

由表3和图5可知，各阶振幅值随着测试管柱壁厚的增大而增大，增幅近似为线性增加；横向横向振动位移随壁厚的增加而增加，靠近泥线上400 m区域的横向位移最大，且随壁厚增大的幅度较大。增大管柱的壁厚时，管柱的强度增大，同时管柱的横向振动增大，加大了测试管柱与隔水管接触的概率。

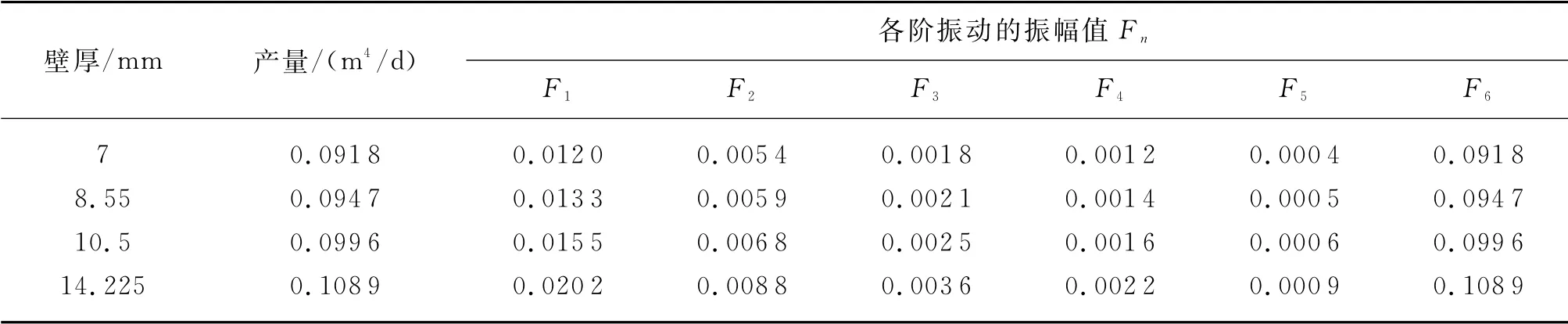
表3 不同测试管柱壁厚对应的前六阶振幅值Tab.3 First six amplitude values corresponding to different test string wall thicknesses

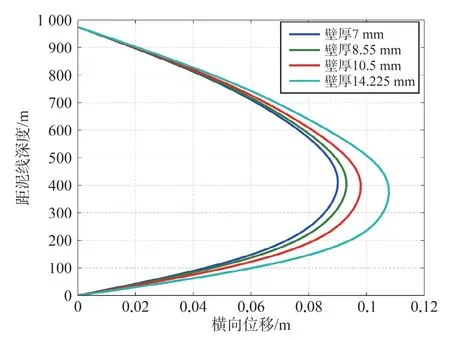
图5 不同壁厚下测试管柱的最大横向振动位移Fig.5 Maximum lateral vibration displacement of test string at different wall thicknesses

3.5 不同产量对测试管柱横向位移的影响

产量测试是深水测试作业的关键部分，产量变化时，测试管柱温压场、轴向力等均会发生变化，基于A井不同产量下的轴向力、流速等参数［19］，获得不同产量下的测试管柱振幅及最大位移，分别如表4和图6所示。

由表4及图6相关结果可知：测试管柱的各阶振幅及最大位移随着测试产量的增加而增大，且近似呈线性增加，但增加的幅度较小，且最大横向振动位移以一阶振幅值为主；深入分析其原因，在井口悬挂力不变的情况下，由于单位长度内气体质量流量和流固间摩阻的增大，泊松耦合和摩擦耦合效应使得自海平面以下的管柱轴向力减小量一定程度上略增，最终引起管柱横向振动位移一定程度的增大。上述结果与已有研究结果［22］的变化趋势基本一致，因此，当测试产量稳定后，产量的变化对测试管柱横向振动的位移影响不是太大，重点注意产量调整过程中振动参数的变化。

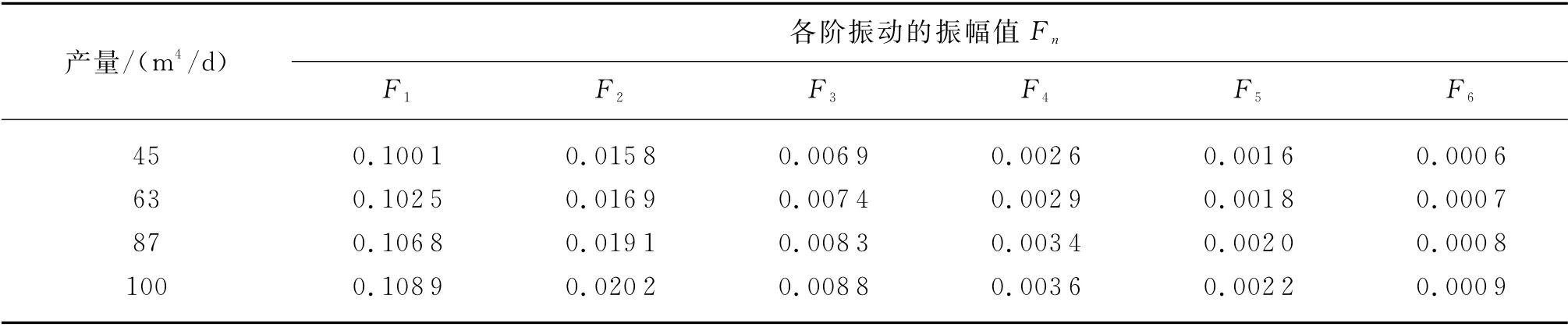
表4 不同产量对应的前六阶振幅值Tab.4 First six amplitude values corresponding to different outputs

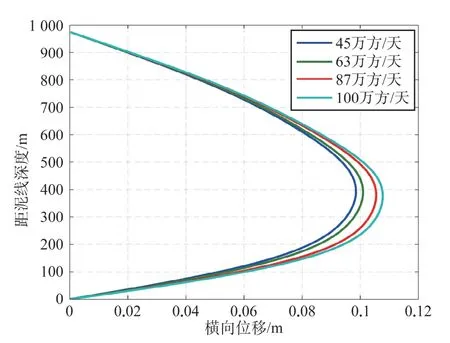
图6 不同产量下的测试管柱最大横向振动位移Fig.6 Maximum lateral vibration displacement of the test string at different production rates

3.6 现场应用

在上述研究的基础上，以我国南海某测试Y井悬挂力的优选为目标。Y井作业水深超过1 800 m，井深超过3 000 m，基于前期的勘探开发经验，现场作业拟使用与A井相同内外径油管和隔水管进行测试，最大测试产量按160万方/天进行设计。根据上述研究结果，水深超过1 600 m时，在环空间隙不增大的情况下，应考虑随水深增大原设计的有效悬挂力（＞20 klbs/100 m），最终计算悬挂力须大于1 310 kN；在考虑到管柱的抗拉强度（最大拉应力630 MPa）及安全系数1.6后，管柱最大悬挂力为1 761 kN。基于极限测试产量200万方下管柱最大横向振动量需小于隔水管与测试管柱环空间隙，该井最终坐挂后的有效悬挂力为1 422 kN（不考虑大钩等悬重）。测试完工后，对作业油管检测和观察，海水段油管未出现明显磨损和弯曲，说明了所推荐悬挂力是合理的。

4 结 语

（1）基于深水测试管柱的横向振动模型的求解结果表明：当测试管柱整体受拉时，测试管柱的最大振动位移随悬挂力的增大而减小；当悬挂力不变时，水深的增加会导致深水测试管柱局部受压，使得各阶振幅及总位移变化较大；当悬挂力随水深的增加相应增大时，测试管柱各阶振幅及最大横向位移随水深的增大而增大，最大横向位移与水深似线性增加。

（2）测试管柱的各阶振幅及最大位移随着测试产量及壁厚的增加而有一定程度的增大，最大横向振动位移均以一阶振幅值为主；当管柱的壁厚增大时，管柱最大横向振动位移增大，会增大测试管柱与隔水管接触的概率。

（3）为了减小隔水管和测试管柱的潜在接触风险，在测试作业水深增大时，为减小测试管柱的横向振动位移，除需等比例增加悬挂力，还应适当增大测试管柱与隔水管间的环空间隙；同时测试现场应关注产量调整过程中测试管柱振动参数的变化，结合管柱强度合理选择壁厚。