基于优化Kriging模型的平台结构动力学模型修正

冷建成， 田洪旭, 徐 爽, 周国强, 赵海峰

(1. 东北石油大学 机械科学与工程学院，黑龙江 大庆 163318； 2. 中国石油集团工程技术研究院，天津 300451)

模型修正是有限元分析的逆命题，受模型简化、加工制造误差、边界条件变化等因素的影响，有限元模型不一定能准确反映结构的真实情况。因此，需要对有限元模型进行修正，使其获得与真实结构相一致的动力和静力响应，这一过程即为模型修正。随着有限元仿真在工程应用中的不断拓宽，模型修正技术也日渐凸显出了其重要性，尤其是在安全性能评估、动态响应预测、结构设计等领域，模型修正技术作为联系数值模型和实体结构间的纽带，在解决工程问题的过程中发挥了关键性作用。

传统的模型修正方法按修正对象可分为矩阵法和元素法两类，前者基于矩阵摄动理论并引入正交性和系统特征方程作为约束条件修正刚度和质量矩阵[1-4]；后者将结构的固有属性，如密度、弹性模量、边界条件等作为修正参数，构建目标函数[5-8]。上述方法由于在修正过程中需要大量的有限元迭代计算，修正效率受到了严重影响，使得模型修正往往需要耗费大量的时间。近年来，为解决这一问题，代理模型法开始应用于模型修正领域。该方法利用代理模型，包括多项式响应面模型、缩阶模型、支持向量机模型、神经网络模型等，代替待修正参数与修正目标间复杂的映射关系，减少了修正过程中的有限元计算量，因而显著提高了修正效率。Fang等[9]提出将D最优实验设计方法和一阶响应面相结合用于解决模型修正问题，并利用钢筋混凝土框架验证了该方法的有效性；宗周红等[10]利用三阶多项式代理模型修正了下白石大桥的初始有限元模型。然而，代理模型在推广过程中也受到了一些质疑，究其原因在于代理模型是具备统计特征的近似方法，存在着近似误差的问题，而模型修正属于一类不适定性问题，微小的干扰可能对最终结果产生较大的影响。为此，有学者从代理模型构造方法出发提出了改进方法。Chakraborty等[11]提出将滑动最小二乘法引入到代理模型生成过程中，认为基于滑动最小二乘的自适应模型修正方法相较于最小二乘法拥有更高的拟合精度。陈喆等[12]提出采用一种混合基函数形式的增广SVM方法构造代理模型，并通过算例说明该方法相较于普通SVM方法有着更高的精度。

源于地质统计学的Kriging模型[13]是一种插值模型，其优势在于对非线性问题有着突出的拟合效果，在优化设计和可靠性分析等领域有着广泛的应用[14-15]。张冬冬等[14]对Kriging模型在模型确认领域的应用进行了探讨，提出利用置信空间评价代理模型的有效性。韩忠华[15]总结了Kriging模型的进展历程，利用机翼优化算例对基于Kriging模型的优化设计理论进行了验证。可见，该方法在航空等工程领域已有成功应用，本文以某导管架海洋平台模型为研究对象，在研究Kriging代理模型修正方法的基础上提出一种基于多目标遗传算法(Multi-Objective Genetic Algorithm，MOGA)的局部加点优化方法以提高Kriging模型精度，并利用平台物理模型试验验证了修正方法的有效性。

1 基本理论

1.1 Kriging模型

Kriging模型认为随机变量的分布规律是在全局期望的基础上受一定的局部偏差影响而产生的，且该局部偏差呈高斯随机分布，通过协方差表示其相关程度

Cov[Z(x),Z(x′)]=σ2R(x,x′)

(1)

式中:Z(x)，Z(x′)为局部偏差；σ2为局部偏差的高斯随机函数方差；R(x,x′)为随机变量中两点相关性的相关函数，与两点距离d和系数θ有关，基本形式为

(2)

得到的拟合结果可写作

y(s)=f(x)+Z(x)

(3)

式中:f(x)为符合全局函数期望的回归函数；Z(x)越趋近于0，拟合曲线越光滑。

在确定相关函数的前提下，Kriging模型可看作由β,σ2,θ组成，利用最大似然估计联合贝叶斯方法，求得β0与σ2分别为

β0=(fTR-1F)-1FTR-1ys

(4)

(5)

式中:F=[f(x1)，f(x2),…，f(xn)];ys为各设计点的响应值，R为相关性矩阵

(6)

记r为相关矢量，rT=[R(x1,x),R(x2,x), …,R(xn,x)]，则最终结果可表示为

(7)

1.2 Kriging模型修正方法

Kriging模型修正方法是在传统模型修正方法求解目标函数这一步骤中，利用Kriging模型代替复杂的有限元计算，其流程如图1所示。可大致概括为3个主要流程：①生成样本空间，主要包括修正参数的选取及试验设计，其中试验设计的目的是在最小化选取样本点数量的同时，最大化获得修正空间内的信息量，主要试验设计方法包括中心复合设计、D最优设计、超拉丁方设计等；②Kriging模型的生成；③修正目标的求解，常引入遗传、粒子群、模拟退火等智能仿生算法以优化求解过程，改善多个修正目标下可能面临的收敛问题。

图1 Kriging代理模型修正框架图Fig.1 Framework of Kriging model based model updating method

2 海洋平台模型修正

2.1 初始有限元模型分析

选取一导管架海洋平台的室内物理模型作为研究对象。该试验模型以某导管架平台为原型，按几何相似比1∶50加工而成，模型总高度为3.506 m，分为7层，底层尺寸为1.739 m×1.447 m，共有8个桩腿，各桩腿通过底部的螺栓固定在底座基础上。对该试验模型进行有限元建模，基于模态分析得到固有频率及振型，如图2所示，其中，前三阶为结构整体振型，分别为纵向弯曲(21.969 Hz)、横向弯曲(23.603 Hz)和扭转(33.785 Hz)。

图2 前三阶有限元计算模态振型图Fig.2 View of the first three modes of vibration obtained by FE model

2.2 模型振动试验

为获取实测模态信息，采用上海北智公司17110型压电式加速度传感器和比利时LMS SCADAS Mobile测试系统对平台进行了力锤敲击试验，在平台模型上共布置了10个测点，如图3所示。

图3 测点布置图Fig.3 View of measurement points

为确保测试结果真实有效，每次敲击均由同一名试验人员在确保模型不受任何外力干扰的情况下完成。测试数据利用LMS Test Lab软件进行处理，由多参考点最小二乘复频域法得出前三阶实测固有频率，并考察频率相关性Eω[16]

(8)

式中：ωt为实测频率；ωa为有限元计算频率，计算结果如表1所示。

表1 平台模型计算模态频率与实测模态频率的比较

2.3 修正参数选择及试验设计

海洋平台可供选择的修正对象包括平台杆件的截面及材料属性、边界条件、甲板附加质量等。由于表1中一阶模态频率实测值与计算值相差较大，将桩腿底部纵向边界条件改为弹性支承，将弹性支承的刚度K设为修正参数，以修正边界条件简化带来的影响，降低一阶频率的计算值。同时将材料弹性模量E、平台外侧桩腿壁厚δ1、中间桩腿壁厚δ2以及顶层甲板厚度t设为修正参数，各参数的取值范围及在有限元模型中的初始值，如表2所示。

表2 修正参数取值范围

试验设计采取拉丁超立方抽样方法，该方法是一种多维分层抽样方法，相较于传统方法能够使选取的样本点布满样本空间，从而避免堆积点的问题[17]。共选取了27个样本点，如表3所示。

表3 拉丁超立方抽样设计

2.4 Kriging模型生成

通过有限元计算得出样本点处的频率值，生成了Kriging模型。将参数K固定为1×107N/m，其余参数固定为初始值，对Kriging模型进行局部灵敏度分析，结果如图4所示。结合分析结果，选取对修正过程有显著影响的参数，绘制响应曲面，如图5所示。

图4 局部灵敏度示意图Fig.4 Local sensitivity diagram

由图4可知，前三阶频率与参数t呈负相关关系，与其余4个参数呈正相关关系。参数K仅对一阶频率有显著影响，参数δ1对一阶频率和二阶频率有显著影响，参数t对前三阶频率均有显著影响，参数E,δ2对前三阶模态频率的影响相对较弱。

响应曲面图能够直观反映模态频率随修正参数变化的趋势。由图5可知，计算模态频率能够在修正域内达到目标值。对Kriging模型精度进行检验，计算均方根误差(Root Mean Square Error，RMSE)如式(9)所示，前三阶频率计算结果分别为3.467×10-9,7.986×10-9,7.611×10-9，均趋近于0，说明Kriging模型能够反映修正参数与模态频率的映射关系，可以用于替代有限元模型进行修正。

(9)

图5 前三阶模态频率响应曲面图Fig.5 Response diagram of the first three modal frequencies

2.5 基于Kriging模型的平台模型修正

利用MOGA在Kriging模型中求解全局最优，得到修正点和近似值，将修正点代入有限元模型中进行验算，得到修正值，如表4所示。

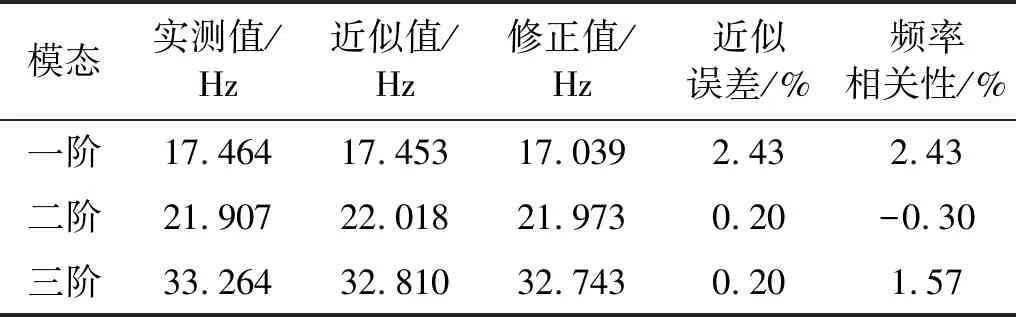
表4 修正结果

由表4可知，基于Kriging模型的模型修正可以获得显著的修正效果，但一阶频率近似误差相较于其余两阶存在较大差距，可能对最终修正结果产生一定影响，由此判断修正过程仍有进一步优化的空间。

3 基于优化Kriging模型的平台模型修正

3.1 基于MOGA的局部加点优化方法

复杂结构中修正参数与目标函数间的映射关系往往具有较强非线性特征，因此需要对代理模型进行优化处理以提高其拟合精度。在修正空间内添加样本点是一种直接有效的优化方法，Kriging模型中常用的加点准则包括最小化代理模型准则、改善期望准则、改善概率准则、均方差准则等。

模型修正问题仅关心最优修正点相近区域的局部拟合精度。针对这一特点，提出一种基于MOGA的局部加点优化方法，认为修正过程中通过MOGA计算得到的Pareto最优解集接近于最优修正点，新增样本点可从中选取。分为两类情况：一类是修正点拟合效果较差且未出现符合期望的修正点，可以通过调整代理模型精度获得更为精确的修正结果；另一类是修正点拟合精度较高，或出现了符合期望的修正点。对于第一类情况，优先选取最大误差点，同时适当增加所选取样本点的数量以加快收敛，如式(10)所示；对于第二类情况，则直接选择修正效果最佳的点，如式(11)所示。

(10)

(11)

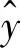
3.2 基于优化Kriging模型的平台模型修正

将基于MOGA的加点优化方法引入到修正流程中，验证Pareto解集中排序靠前的4个解，从中选择新增样本点并更新Kriging模型重新进行修正，循环7次，结果如表5所示。

同时定义平均修正误差和平均拟合误差分别如式(12)和式(13)所示，其变化如图6所示。

(12)

(13)

图6 修正和拟合误差变化示意图Fig.6 Modification and fitting error diagram

表5 基于MOGA加点优化法的前7次循环修正结果

前两次循环属于第一类情况，分别选取了3个和2个新增样本点，修正后平均修正误差和平均拟合误差分别降至0.257%，0.041%。第三、第四次循环属于第二类情况，经过优化后近似误差和修正误差均有回升。第五、第六、第七次循环按第一类情况选取新增样本点，最终平均修正误差和平均误差拟合降至0.271%,0.154%。从表5中可知，Kriging模型中的近似误差主要集中在一阶频率，但在循环过程中，二阶、三阶频率的修正同样出现了波动，循环过程中变化较大参数是δ2和t。第三次循环后，平均修正误差达到了最低值0.238%，且修正后前三阶计算频率相关性均达到了理想水平，可将其视为最终修正结果。

4 结 论

通过试验与有限元模拟，基于Kriging模型修正方法对室内导管架平台数值模型进行了修正。为提高Kriging模型的拟合精度，提出了一种基于MOGA的优化方法，得出以下结论：

(1) 以拉丁超立方抽样设计抽取样本点所构建的Kriging模型能够有效反映出海洋平台结构参数与模态频率间的映射关系，且分析效应和计算精度高，可以应用于海洋平台的模型修正问题中。经过修正后，前三阶模态频率相关性由-25.80%,-7.74%,-1.56%修正至2.43%,-0.30%,-1.57%，效果显著。

(2) 代理模型的近似误差对修正结果有一定的干扰，不仅会对出现误差的目标造成影响，还可能使其余目标函数的修正出现偏差。提出的基于MOGA的加点优化方法能够对Kriging模型进行局部优化处理，大大提高了拟合精度，提升其修正效果，进而验证了所提方法的有效性，并可推广到其它实际工程结构的有限元模型修正中。