振动响应传递率及其工作模态分析方法综述

李星占， 岳晓斌， 黄 文， 董兴建， 彭志科

(1.中国工程物理研究所 机械制造工艺研究所，四川 绵阳 621900；2. 上海交通大学 机械系统与振动国家重点实验室，上海 200240)

模态分析在实际的工程应用中有着重要的意义，它可以评价现有结构的动态特性，避免共振，控制噪声，为结构的优化设计提供指导[1]。传统上获得结构模态特性的实验方法为实验模态分析(Experimental Modal Analysis, EMA)。通常使用模态力锤或激振器激励结构，使用传感器采集结构的响应；根据定义，计算结构的频响函数；根据辨识算法，获得模态参数(固有频率、模态阻尼和模态振型)。在实际应用中，EMA的应用有很大的局限性：需要结构的激励信号。但是，鉴于结构的特点与工作环境，一些结构很难人为的激励或者激励信号无法测试，如桥梁由于结构太大无法人工激励[2-3]，海上风力发电机的风载和波浪激励无法准确测量[4-5]，高速旋转的主轴由于危险无法锤击激励[6-7]。此时，工作模态分析(Operational Modal Analysis, OMA)方法被提出，在未知输入的情况下，辨识结构的模态，如峰值提取(Peak Picking, PP)法、频域分解(Frequency Domain Decomposition, FDD)法、多参考点最小二乘复频域(Poly-reference Least-squares Complex Frequency Domain, PolyMAX或PolyLSCF)法、随机子空间(Stochastic Subspace Identification, SSI)法和特征系统实现(Eigensystem Realization Algorithm, ERA)法等[8-9]。OMA方法的优势在于无需已知输入信号，能在工况下在位测量，但对于输入的类型有一定的限制：在所关心的模态分析区间，激励信号必须为平稳随机信号。因此，当激励信号为有色噪声或者混有谐波信号等时，OMA方法无法准确的区分结构自身的模态频率和由激励信号带来的虚假模态频率，需要通过其它算法来辨识虚假模态，这增加了OMA方法应用的难度，降低了辨识结果的可信度。

基于振动响应传递率的OMA方法由Devriendt等[10]在2006年提出。该方法最大的特点就是辨识结果可以不受输入类型的影响，无论是有色噪声、正弦扫频，还是锤击激励，被激励模态的参数都能被正确的辨识，虚假模态能被有效的区分。该优势使得基于振动传递率的OMA方法能够在其它方法不适用的情况下应用，但在该方法中也存在缺陷。基于传递率的OMA方法需要两次及以上不同激励情况下的响应，且响应参考点的个数必须大于激励源的个数。

基于以上原因，为更好的利用基于传递率的OMA方法，近十年来，国内外许多学者对该类方法进行了大量的研究和拓展，并将其应用于多个领域。为了深入的分析该方法，将从以下三个方面对振动传递率及其OMA方法进行了综述。首先，对振动传递率概念的发展及研究现状进行介绍；其次，对传递率的估计方法进行了介绍；然后，对基于传递率的各种模态辨识方法进行了综述，重点分析方法的原理，比较方法之间的优缺点，并为以后该类方法的发展进行展望。最后，在综述的基础上，选择四种代表性的辨识方法，对不同激励情况下的多自由度系统模型进行了模态辨识，比较了参数辨识的结果及各方法的局限性。

1 传递率的概念

在20世纪90年代之前，振动传递率的概念通常限定在单自由度系统中，分为响应传递率和力传递率。如图1所示的单自由度集中质量-弹簧-阻尼系统，集中质量与系统的基座之间响应的关系可以用传递率的形式表示为

(1)

式中：TAB为A，B之间的响应传递率;Y(s)为响应y(t)的Laplace变换;m,c,k分别为单自由系统的质量、阻尼和刚度。

图1 单自由度系统Fig.1 Single DOF system

单自由度系统中响应传递率的定义表示了振动在通过系统前后的响应比，可用来表示振动的衰减情况，调节系统的参数，可控制振动的衰减。力传递率与响应传递率相似，定义为集中质量与系统基座之间受力的比值。Ungar[11]通过分析和推导证明，在单自由度、线性、单轴系统中响应传递率与力传递率是相等的。

随着结构的大型化、复杂化，以及人们对结构监测要求的提高，如何根据测试获得的部分响应或力去估计和预测未测试或者无法测试部分的响应或力成为困扰研究人员的一个难题。因此，将振动传递率从单自由度系统推广到多自由度系统变得非常有意义。Paipetis等[12-15]对特定形式的多自由度系统中振动传递率的定义进行了探索。1998年Ribeiro等[16]首次提出了通用化的多自由度系统中传递率的概念，通过频响函数建立已知响应矩阵和未知响应矩阵之间的关系。Maia等[17-18]对多自由度系统中传递率的概念进行了进一步的阐述，并提出了传递率矩阵的计算方法。第一种方法是通过结构的导纳矩阵运算，第二是通过结构的响应矩阵直接获得。Fontul等[19]对传递率矩阵在随机和谐波振动过程中的特性进行了解析和仿真验证，结果再一次证明振动传递率矩阵不受激励力类型的影响，而取决于激励、已知响应和未知响应所处的位置。Maia等[20]对多自由度系统中传递率概念的发展进行了综述。Lage等[21]对力传递率和位移传递率之间的关系进行了研究。

如图2所示的多自由系统，A,K,U,C分别为激励力、已知响应、未知响应和其它响应的坐标集合。依据频响函数，激励和响应之间的关系可表示为

(2)

式中：Y,H和F分别为响应向量、频响函数向量和力向量。

图2 多自由度系统及其坐标集合Fig. 2 MDOFs system and its coordinates sets

通过矩阵运算，消除力向量，获得多自由度系统中已知响应与未知响应之间的关系

YU=TUKYK

(3)

其中，

TUK=HUA(HKA)+

(4)

即为未知响应与已知响应之间的传递率矩阵。(*)+为矩阵的伪逆矩阵，为使矩阵有意义，需满足K的个数大于等于A的个数，即已知响应的个数不能少于激励点的个数。

多自由度系统中传递率概念的提出与完善，促进了传递率在结构响应估计[22]、损伤检测[23]、频率响应函数的估计[24]、力辨识[25]和传递路径分析[26]等方面的应用。特别是在OMA领域，基于振动传递率的特性，该类方法得到的迅速的发展。同时，在多自由度系统传递率的框架下，一些新的传递率的概念被提出。图3展示了传递率概念的发展和衍化。

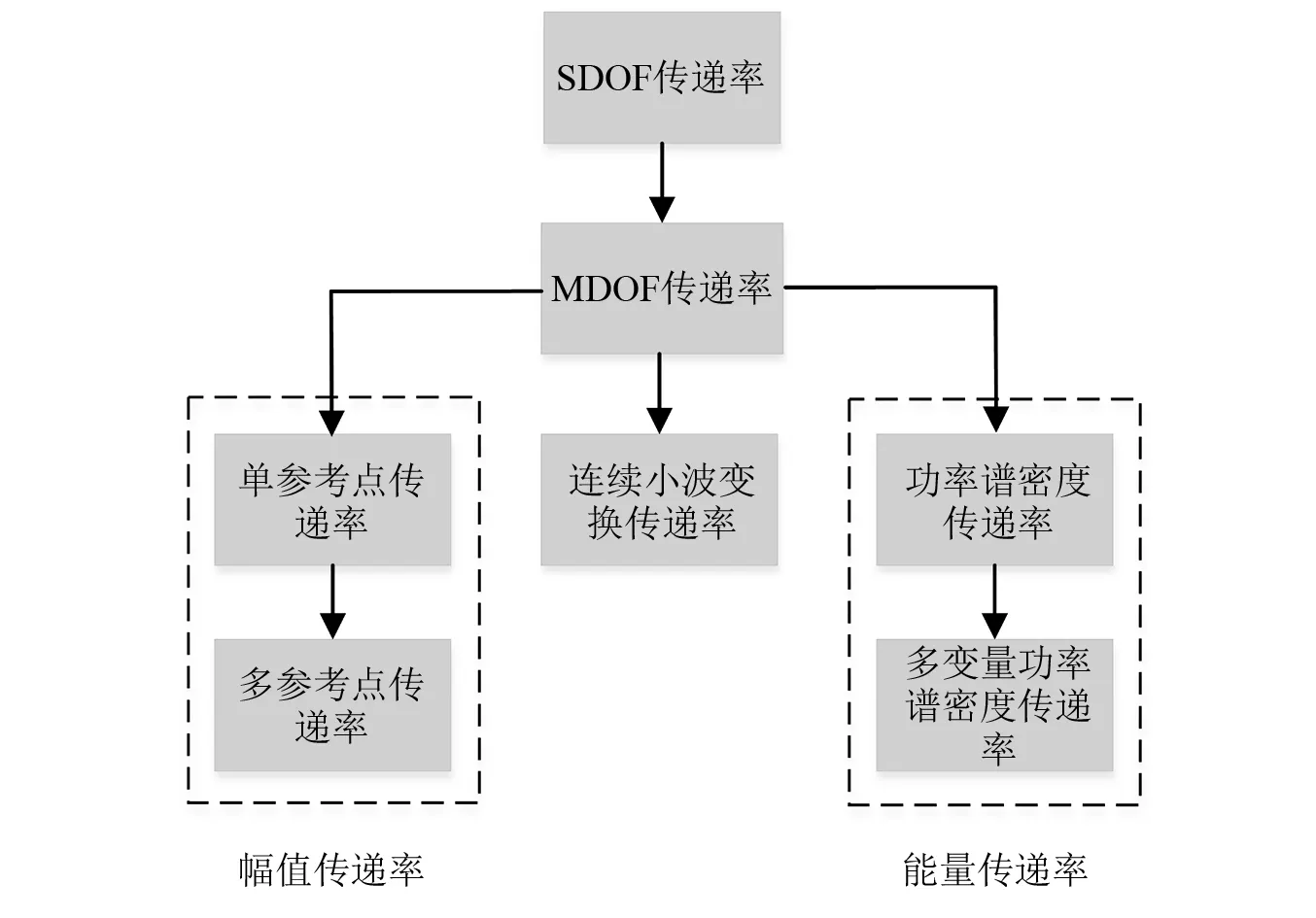
图3 传递率概念的发展和衍化Fig.3 Concept development of transmissibility

1.1 单参考点传递率

当系统中参考输出点的个数只有一个时，传递率矩阵可以进行简化，任意非参考点L与参考点R之间的单参考点传递率(Single Reference Transmissibility Function, STF)可表示为[27]

(5)

式中：Ni为激励的个数。

1.2 多参考点传递率

当系统中参考输出点的个数大于一个时，多参考点传递率(Poly-reference Transmissibility Matrix, PTF)可表示为[28]

(6)

式(6)与式(4)的定义完全一样。因此，严格意义上来说，多参考点传递率并不是一个新的概念，而是多自由度系统传递率从参考点个数角度的重新命名。

1.3 功率谱密度传递率

以上两种传递率的定义都是从响应谱的角度，依据多自由度系统传递率的概念直接演化获得的。考虑从能量的角度重新定义传递率，在非参考输出点和参考点之外，增加一个系统性的输出参考点P，功率谱密度传递率(Power Spectrum Density Transmissibility, PSDT)可表示为[29]

(7)

式中:Syy为响应之间的互功率谱密度。

1.4 多变量功率谱密度传递率

考虑多个传递输出参考点，将功率谱密度传递率推广到多变量功率谱密度传递率(Multivariable Power Spectrum Density Transmissibility, MPSDT)[30]

(8)

式中：Z为传递输出参考点的集合；(*)T为矩阵的转置。

1.5 连续小波变换传递率

傅里叶变换可以将信号从时域转换到频域，但其分析的分辨率是固定的。与之相比，小波变换的多尺度分析可以对信号的特征进行更好的提取。将小波变换替代傅里叶变换，与功率谱密度传递率的概念相结合，提出连续小波变换传递率(Continuous Wavelet Transmissibility, CWTR)的概念[31]

(9)

式中：av为尺度因子；CSyLyP和CSyRyP分别为L和P，R和P响应之间基于连续小波变换的互功率谱密度。

2 传递率的估计方法

从传递率的定义可知，振动传递率可以由系统的动力学参数或传递函数获得。但在实际应用中，动力学参数或传递函数很难直接获得，振动传递率通常由系统的响应计算，且考虑到系统中噪声的影响，需采用估计类的算法。

2.1 非参数化估计方法

在经典的振动理论中，H1,H2和Hv估计算子可以用来估计传递函数。传递率的非参数化估计方法建立在这些经典算子的基础之上。

Fontul等对谐波激励和随机激励下传递率矩阵的计算方法进行了研究，提出仅通过响应之间的互功率谱矩阵即可计算传递率矩阵，并将通过该方法与通过频响函数计算获得的传递率进行了比较，验证了方法的准确性。Devriendt等[32]提出单参考点传递率可以通过参考点和非参考点之间的互功率谱和自功率谱，采用H1估计算子进行计算。Mao等[33]指出通过H类估计算子进行传递率估计时，功率谱密度的估计会给结果引入计算误差，因此提出采用参考点和非参考点自功率谱比值的均方根来估计传递率的幅值。Leclere等[34-35]认为输出之间的信噪比接近，因此采用Hv估计传递率。仿真和实验结果的对比发现，Hv估计要比H1和H2估计的结果更好。张永年[36]提出可以用H1,H2,H3,H4和Hv对传递率进行估计，并对几种估计方法的计算结果进行了对比，发现Hv估计在含噪声情况下的估计效果最佳。

通过以上介绍，传递率通常有以下几种估计方法。

H1估计

(10)

H2估计

(11)

Hv估计

(12)

式中：Nr为参考点的个数；No为输出的个数；V(s)为响应矩阵SVD分解的右矩阵。

2.2 参数化估计方法

另一类估计传递率的方法是使用参数化估计算子。与非参数化估计方法相比，参数化方法不需要将时域响应进行分段，也不需要对数据进行任何形式的加窗。尽管这会造成一定程度的泄露，但是参数化模型会对这些泄露进行补偿。张昱[37]通过分析指出，在输入不完全相干的情况下，激励之间的不相干性会大大降低估计结果的可靠度，因此通过参数化系统辨识方法要比非参数化估计方法更加准确。

Devriendt等[38]提出可以采用最小二乘类估计方法对传递率的公分母模型进行参数化估计。与频响函数的估计方法类似，通过该参数化估计可以求解系统的模态参数。张永年等[39]提出采用幂多项式有理分式的形式估计传递率，基于Forsythe正交多项式可减少求解过程方程的病态性并解耦系统矩阵，进而通过最小二乘拟合获得系统的模态参数。

由以上分析，传递率的参数化模型可以表示为左矩阵分式的形式[40]

D(s)yL(s)=N(s)yR(s)+τ(s)

(13)

其中，

(14)

(15)

(16)

式中：Nd为分母矩阵多项式的模型阶数；Nn为分子矩阵多项式的模型阶数。

基于获得测量数据，采用最小二乘法、总体最小二乘法和极大似然估计法等[41]方法，可以对模型中的未知系数Ai和Bi进行估计。获得估计的系数后，传递率的参数化模型即可表示为

(17)

由式(17)，即可获得参数化估计的传递率。

以上两种传递率的估计方法主要针对幅值类的传递率。对于能量类和小波类的传递率，在传递率的定义中都给出了准确的估计方法，因此，其计算过程主要依据概念的定义进行。

3 基于传递率的工作模态辨识方法

根据图3所示的传递率概念的发展过程，将依据传递率进行工作模态分析的方法分为三类：基于幅值类传递率的OMA方法、基于能量类传递率的OMA方法和其它基于传递率的OMA方法。

3.1 基于幅值类传递率的OMA方法

Devriendt等[10]在2006年提出采用单参考点传递率进行工作模态分析。通过对传递率的分析，发现两点之间响应的传递率在系统极点处趋近于两点之间该阶模态的振型向量之比，在不同激励情况下同样位置之间的传递率在极点处的差值趋近于零。基于此，提出了最原始的基于传递率的工作模态分析方法。

(18)

(19)

式中：A，B，C分别为不同的激励情况。该方法与FDD方法中采用响应的功率谱密度矩阵进行SVD分解，进而指示模态位置的思路是一致的。之后，Devriendt等对基于传递率的方法在同时受到多个激励，且激励中带有谐波频率的情况进行了实验分析和验证。结果显示，模态参数的辨识结果没有受到激励中谐波成分的影响，在辨识的过程中无需对系统中的频率成分有先验知识。

(20)

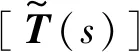
在对单参考点传递率的深入分析中，Devriendt等[45]发现，当系统中只有一个激励时，单参考点传递率是确定的，激励中的随机成分都被消掉；而当系统中存在多个激励时，虽然在极点处传递率趋近于模态振型向量的比值，但激励并没有完全消除，单参考点传递率受到激励中随机成分的影响，不再是确定性的。因此，在模态辨识的过程中存在不确定性。由此，提出采用多变量传递率进行模态辨识。多变量传递率又称为多参考点传递率，独立于系统的输入，不受激励的影响，但不再相交与系统的极点。通过分析，采用类似于空间投影的方法，由多变量传递率求解新的单参考点传递率，该传递率只与响应点的位置有关，不受其它激励和位置的影响。由此，基于多变量传递率的工作模态分析方法可以表示为

(21)

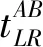
基于多变量传递率投影的方法虽然解决了在多激励情况下，基于多变量传递率的模态识别问题，但在计算的过程中需要至少三种不同的激励状态，这在实际的应用中是非常困难的。为此，Weijtjens等[46]提出了一种新的基于多参考点传递率的辨识方法。该方法对多参考点传递率进行重新构造，使其与模态向量矩阵正交。由此，基于参数化估计方法，将系统极点的求解转换为一个非线性特征值问题

γ(λm)φm=0

(22)

式中：λm为系统的特征值点；φm为系统的特征向量；γ为由多参考点传递率的参数化估计系数重构的矩阵。应用PolyLSCF方法，求解特征值问题，即可获得系统极点的稳定图。与之前基于多变量传递率的方法相比，多参考点传递率方法只需两次不同激励情况下的响应，且基于稳定图的算法结果更加稳定。之后，Weijtjens等[47]又对该方法进行了进一步的阐述。与SSI方法对比发现，基于多参考点传递率的OMA方法中系统特征值的偏差和标准差更小，辨识结果更加准确。周思达等[48]提出了一种改进的基于多参考点传递率的模态辨识方法。基于左矩阵分式多项式模型，利用正则方程Jacobi矩阵的分块性质对最小二乘问题矩阵形式进行缩减，降低了计算量；通过高维伴随矩阵方法解决了矩阵多项式的特征值求解问题；并通过两个数值算例对方法进行了验证。

在应用传递率进行OMA分析时，一个重要的问题是如何获得两次以上不同激励的响应，即如何确定存在不同的激励。针对这一问题，Weijtjens等[49]提出了一种基于时变单参考点传递率的OMA方法。方法认为系统的输入为时变载荷，而在任意一个时刻，瞬态传递率可以看做某一特定激励下结构的传递率，因此获得多个瞬态传递率即可利用单参考点传递率的方法辨识系统的极点

(23)

式中：t1，t2为两个任意的瞬时时间；TLR(s,t1)和TLR(s,t2)为两个时间点的瞬时单参考点传递率。该方法的优点在于无需再去区分不同的激励状况，不足之处是只能在单个输入或单个分布输入下基于单参考点传递率进行模态辨识。之后，Weijtjens等[50]结合时变单参考点传递率与多参考点传递率，将该时变传递率的方法推广到时变多参考点传递率。通过在有色噪声激励下的仿真分析，证明该方法能够很好的辨识出结构的参数，且不受激励中有色噪声成分的影响。

另一个在OMA中普遍存在的问题是，由OMA计算获得的振型并不是真正的振型[51]，只是结构的工作变形形状(Operational Deflection Shape, ODS)。当结构的模态分布比较离散，没有耦合时，ODS主要有单一的模态振型决定，可视为等比例的模态振型；当结构存在密集模态时，模态存在耦合，ODS受到相邻的两个或者多个模态的影响，是多个模态振型的线性叠加，此时ODS无法视为等比例的模态振型。Devriendt等[52]提出了一种基于传递率的模态振型求取方法。将两次不同激励下的传递率矩阵，通过转化，构造为与FRF形式类似的伪频响函数矩阵

(24)

其中，

(25)

然后利用频域参数化估计方法对公分母矩阵模型进行模态参数的识别，获得结构的模态振型。Weijtjens等[53]提出了一种依据多参考点传递率进行模态振型求解的方法。建立多参考点传递率与比例因子之间的关系，利用总体最小二乘方法求解，并将比例因子应用于重构伪传递函数方程。仿真和实验对提出的算法进行了验证，并分析了在测量和任意噪声下伪传递函数的辨识误差。

3.2 基于能量类传递率的OMA方法

Yan等[29]在2012年提出了采用PSDT进行OMA的方法。在系统的极点处，PSDT趋近于模态向量的比值。基于此，利用不同参考点下PSDT的差值，计算传递率差值函数倒数的平均正则方程(Averaged Normalized Inverse Transmissibility Subtraction Function, ANITSF)，即可辨识系统的模态频率。

(26)

其中，

(27)

与采用幅值类传递率进行OMA的方法不同的是，基于PSDT的OMA方法只需单次激励下的振动响应即可，解决了幅值类传递率方法中关于不同激励情况的分析和选择难题。

但是，类似于经典的PP方法，ANITSF方法存在两个缺点：首先，方法只能获得系统的模态频率和离散模态振型，无法计算系统的模态阻尼；其次，极点选择具有主观性，容易出现虚假极点。Araújo等[54]提出了一种改进的基于PSDT矩阵的OMA方法。该方法将基于不同参考点的PSDT組集为一个矩阵，矩阵在系统的极点处趋近于秩为一的振型向量比值矩阵，对该矩阵进行SVD分解，获得奇异值，指示系统的极点。

(28)

类似于经典的FDD方法，该方法充分利用测试数据，能够避免错误计算极点的识别，但还是只能识别模态频率与振型。之后，Araújo等又提出了一种新的基于MPSDT的OMA方法。类似于多参考点传递率，该方法将PSDT矩阵推广到基于不同参考点的多变量PSDT矩阵。在极点处，多变量PSDT矩阵趋近于秩为一的振型向量乘积矩阵。构建基于不同参考点的多变量PSDT矩阵，对该矩阵进行主分量裁剪，消除矩阵中的噪声成分；求矩阵的伪逆矩阵，利用PolyLSCF拟合，辨识系统的固有频率、阻尼和模态振型。相比于之前的两种PSDT方法，该方法获得了模态辨识的稳定图，辨识结果的稳定性、可靠性更高。

此外，Yan等[55]也提出了一种参数化的基于PSDT-LSCF的OMA方法，对ANITSF方法进行了改进。该方法将不同参考点下的单参考点PSDT组成矩阵，利用公分母模型，基于PSDT差值函数倒数的有理方程，利用LSCF方法拟合求解频率和阻尼，基于PSDT矩阵留数的SVD分解求解振型。仿真和实验结果表明该方法计算的参数更加准确，对噪声的鲁棒性更强。最近，Araújo等[56]提出将PSDT与盲源分离相结合辨识低信噪比下结构的密集模态。

3.3 其它方法及应用

以上基于幅值类传递率和能量类传递率的OMA方法是目前基于传递率进行模态分析的主要方法。此外，Yan等[31]在2013年提出了一种基于CWTR的OMA方法。对CWTR的特性进行了分析研究，建立了以ANICWTSF(Averaged Normalized Inverse CWTR Subtraction Function)为基础的OMA指示因子，辨识结构的频率和振型。通过仿真和实验，基于不同的小波函数对结构的模态进行了辨识，且与PP，SSI和有限元方法进行了对比，结果显示该方法能够很好的辨识出结构的模态参数。

在以上基于传递率的OMA方法的基础上，针对传递率及其OMA方法的特性，许多学者也进行了相应的研究。张昱等[57-58]对多自由度系统中传递率的特性及PSDT的作用原理进行了研究和分析。证明了多激励作用下多自由度系统中标量传递率在某些条件下具有不变性，提出了该性质统一的适用模型；探讨了PSDT与模态参数和激励中有色成分的关系，分析了不同荷载条件下能够对PSDT产生影响的因素。Mao等[33]研究了振动传递率幅值估计过程中的不确定性。根据卡方二重检验分析方法，建立了传递率与估计方法、噪声之间的不确定性关系，采用蒙塔卡洛方法进行了不确定性分析。分析结果表明，传递率的估计方法对不确定性不敏感，但传递率对于噪声的不确定性较为敏感。Yan等[59-61]对传递率的统计学特性进行了分析，发现在系统的极点附近，传递率方程仅受信号信噪比和模态振型向量的对比，再次说明信噪比对传递率的估计存在重要的影响。

基于以上传递率的OMA分析方法和特性分析，该类方法在许多工程实践中得到了应用。Devriendt等[62]将基于传递率的方法应用于桥梁的OMA分析，与基于功率谱密度进行OMA分析的方法相对比，由传递率获得的模态更加准确，识别出了更多的模态。De Sitter等[63]将基于传递率的OMA方法应用于声学系统的模态辨识中，提出一种增强的稳定图，对图书馆的声学模态进行了辨识。王泽飞等[64]将传递率法应用在高速齿轮箱箱体工作模态分析中，可用于齿轮箱箱体在线模态监测。周思达等将基于多参考点传递率的OMA方法应用于空间飞行火箭的模态辨识中。韩杰[65]分析了基于传递率的OMA方法，并通过对悬臂梁的振动测试，验证了基于传递率和PSDT两类方法进行OMA分析的有效性。Tsai等[66]将基于传递率的OMA方法应用于机床直线导轨滚珠轴承预紧力变化的监测。Maamar等[67-68]利用基于传递率的OMA方法对切削状态下的机床等的动力学特性进行了辨识，消除了激励中谐波信号对辨识结果的影响。Yan等和Araújo等将基于PSDT的方法应用于桥梁结构的模态测试与状态监测。Khodaygan[69]将PSDT和PolyLSCF方法相结合对非对称主轴系统的模态参数进行辨识。

4 数值算例

为进一步对比分析基于振动传递率的工作模态分析方法，及其与传统OMA方法的不同，以图4所示的一维四自由度弹簧-阻尼-质量系统为计算模型，选择Weijtjens等提出的基于传递率矩阵的PTOMA方法、Araújo等提出的基于PSDT矩阵的PSDTM-SVD方法、传统OMA方法中常用的FDD方法[70]和PP方法[71]，分析在不同输入情况下各个模态辨识方法结果的准确性，以及其受输入成分的影响情况。

图4 四自由度系统Fig.4 Four DOFs system

四自由度系统中，m=1 kg，k=1 000 N/m，c=0.5 N/(m/s)，采用Newmark方法计算梁的响应，系统的理论固有频率分别为3.11 Hz,5.92 Hz,8.14 Hz,9.57 Hz。

表1所示为五种不同的激励情况。Case 1中激励为白噪声，图5所示为白噪声激励下系统的响应频谱，响应中清楚的显示出四个峰值；Case 2中激励为有色噪声，谐波频率为4 Hz，图6所示为有色噪声激励下系统的响应频谱，响应中清楚的显示出五个峰值，系统响应中的频谱显示为系统自有模态特性和激励信号特性的综合。采用四种OMA方法对以上两种情况进行模态辨识，其辨识的结果如图7和图8，虚线指示理论模态频率的位置。

表1 不同的激励情况及属性

图5 Case 1白噪声激励下响应的频谱图Fig. 5 Response spectrum under white noise excitation of Case 1

图6 Case 2有色噪声激励下响应的频谱图Fig.6 Response spectrum under colored noise excitation of Case 2

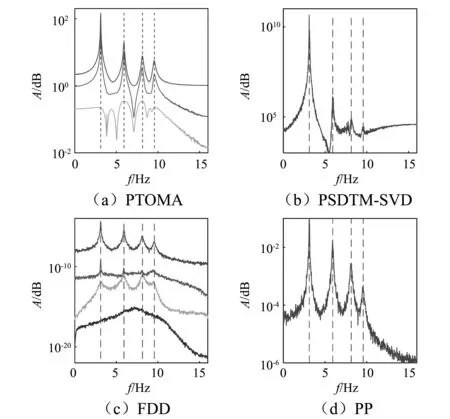
图7 Case 1情况下不同OMA方法的辨识结果Fig.7 OMA results with different methods under Case 1

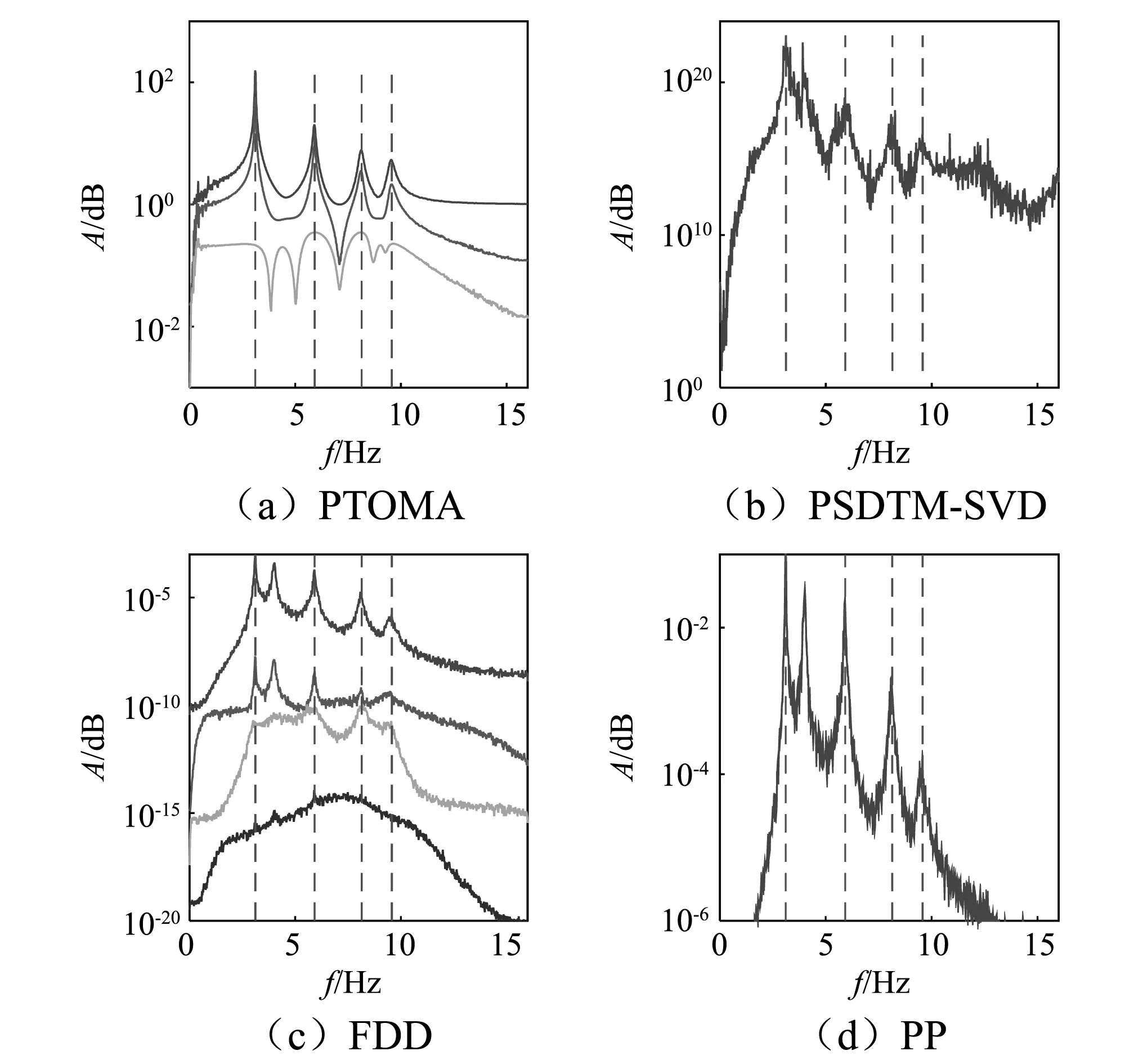
图8 Case 2情况下不同OMA方法的辨识结果Fig. 8 OMA results with different methods under Case 2

Case 3中采用多点激励，激励为白噪声，如在和处同时用白噪声激励下系统；Case 4中激励为有色噪声，谐波频率为4 Hz，在多点同时采用不同信噪比的有色噪声激励系统。采用四种OMA方法对以上两种情况进行模态辨识，其辨识的结果如图9和图10。

对以上四种情况下的辨识结果进行提取，获得的OMA辨识的系统模态频率如表2～表5。对比表2和表3，在单个白噪声激励的情况下，四种方法都能准确的辨识结构的模态频率；而当受到有色噪声影响时，只有PTOMA方法能够将系统的模态和激励成分中的虚假模态辨别出来。对比表4和表5，在多个白噪声激励下，四种方法都能准确的辨识出系统的模态频率，基于振动传递率的PTOMA和PSDTM-SVD方法在高频段受到噪声信号的影响；在多个有色噪声信号的激励下，只有PTOMA能够完全正确的辨识系统的模态频率。

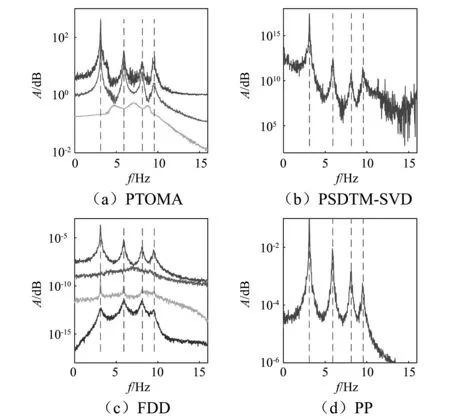
图9 Case 3情况下不同OMA方法的辨识结果Fig.9 OMA results with different methods under Case 3

图10 Case 4情况下不同OMA方法的辨识结果Fig.10 OMA results with different methods under Case 4

模态阶次PTOMAPSDTM-SVDFDDPPf/Hzf/Hzf/Hzf/Hz13.113.113.113.1125.925.895.915.9238.138.168.068.0649.539.679.59.53

表3 Case 2中不同OMA方法辨识的模态频率

表4 Case 3中不同OMA方法辨识的模态频率

表5 Case 4中不同OMA方法辨识的模态频率

对以上四种情况综合分析发现：(1) Araújo等提出的PSDTM-SVD方法虽然基于功率谱密度传递率，但在本算例中，其辨识的结果受到了激励中有色噪声的影响，不能区分系统的模态和虚假模态；结合文献中对该方法的应用，认为该方法的辨识结果不稳定，可能受到系统输入的影响。(2) 基于系统输出功率谱密度的PP和FDD方法受到输入的影响，不能正确的辨识系统的模态频率，但通过几个算例，发现两种方法的计算结果非常稳定。(3) 在四个算例中，只有PTOMA方法能完全正确的辨识系统的模态，再次证明基于单参考点传递率的OMA方法适用于多激励的情况。

5 结 论

针对振动响应传递率及其在工作模态分析领域的发展现状进行了综述，包括振动响应传递率的概念及其发展过程、振动响应传递率的估计方法和振动响应传递率在OMA领域的研究现状。综合数值算例对四种不同OMA方法的对比可知，基于振动传递率的工作模态分析方法能够准确的辨识系统的模态参数；鉴于传递率在极点处的特性，在多次不同情况激励下，利用振动传递率进行工作模态分析可避免受到激励中非白噪声成分的影响，适用于工作状态下存在谐波激励的系统的模态分析。

但是，目前基于振动传递率的方法也存在不足，仍需进一步的研究和探索：

(1) 基于PSDT的工作模态分析方法虽然可以在单次激励的情况下辨识系统的模态参数，但在辨识的过程中算法并不稳定，可能受到激励成分的影响，需进一步改进该类算法，提高辨识结果的稳定性。

(2) 在工况下，系统的模态可能随着时间的变化发生改变。将时频分析方法和基于传递率的OMA方法相结合，研究针对非平稳系统的工作模态分析方法在结构健康监测中有非常大的应用价值。

(3) 系统的物理参数、边界条件等可能存在不确定性，将不确定分析与基于传递率的OMA方法相结合，研究针对不确定性系统的工作模态分析方法具有很大的实用意义。